基于扰动观测器的逆变器并联控制策略研究
朱建忠,葛家宁
(1. 南京工程学院电力工程学院, 江苏 南京 211167; 2. 常州供电公司, 江苏 常州 213161)
微电网由分布式电源小电力系统、负荷和储能装置组成,可以实现自我控制和自我管理[1].微电网是连接分布式发电和大电网、可再生能源和大电网的桥梁,并具备缓冲作用[2].近年来,随着分布式发电的大量运用和微电网规模的不断扩大,逆变器作为微电网中分布式电源与大电网或负荷连接的核心设备越来越受到人们的关注[3].一方面,多个逆变器并联运行可以降低单个逆变器所受的电流应力,提高供电系统的冗余度,保证系统供电的可靠性;另一方面,逆变器并联有利于扩展系统容量,满足用户多种供电要求,体现了微电源即插即用的特征[4].
由于传统逆变器采用dq轴解耦后的双闭环控制[5],其内部为电流控制,外部为电压控制,且都采用PID控制策略.虽然PID控制对扰动有一定的抑制能力,但PID是一种反馈控制方法,只有输出产生波动以后才会有补偿信号,并且积分项的存在降低了补偿速度,因此PID控制器不是抑制扰动的完美策略.负载电流的变化作为逆变器的常见未知扰动,对系统的时间调节等调节性能带来巨大挑战.系统的电感和电容在运行过程中出现参数漂移,使得系统的运行性能下降.当逆变器并联运行时,负载的投切会导致逆变器间的功率震荡,从而威胁到系统的稳定性[6].针对以上问题,本文设计了一种具有扰动抑制能力的并联逆变器控制策略.
1 扰动观测器的基本原理
扰动观测器(disturbance observer, DOB)的基本原理是将含有外部扰动和系统参数扰动的实际模型和不含任何扰动的名义模型作比较,两者的差值就是作用到被控对象上的扰动总和,将得到的总扰动前馈到控制器的输入端进行消除[7].其基本结构如图1所示.
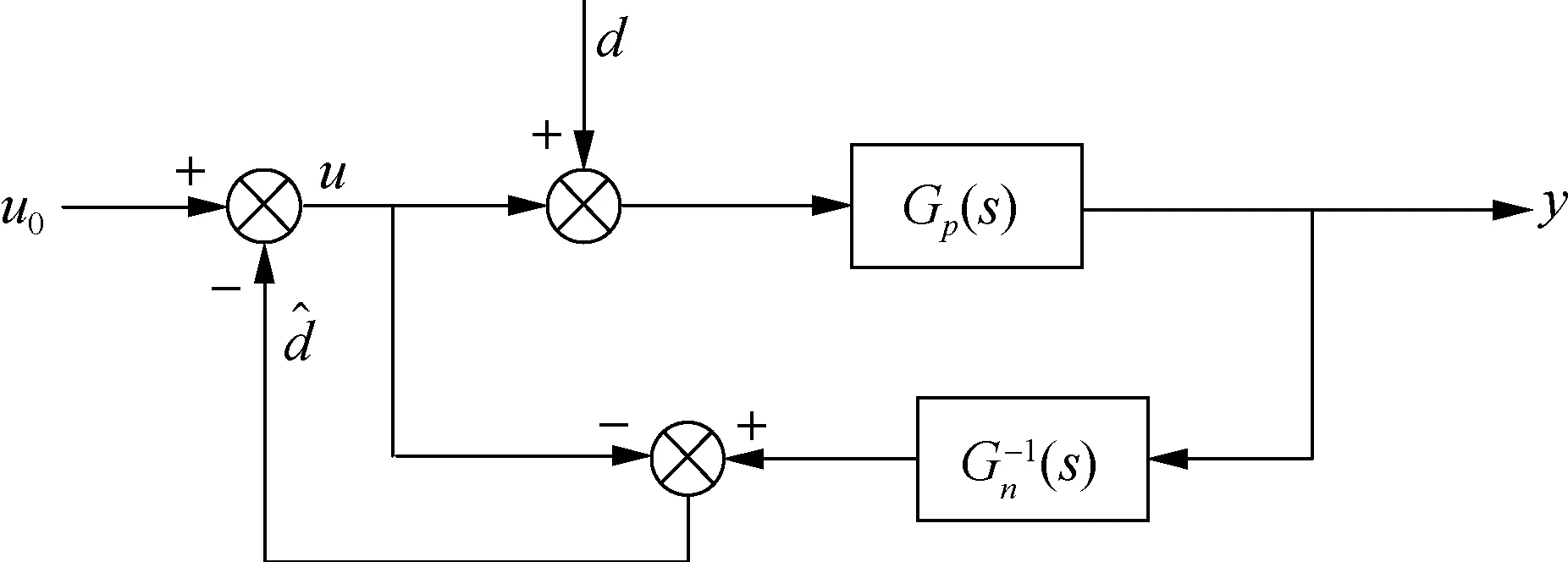
图1 扰动观测器原理框图

图2 扰动观测器结构图
由图1、图2可知,扰动观测器的传递函数为:
y=Guy(s)u+Gdy(s)d+Gξy(s)ξ
(1)
(2)
(3)
(4)
当Q(s)≈0时,式(2)、式(3)、式(4)分别为:
Guy(s)≈Gdy(s)≈Gn(s),Gξy(s)≈0
(5)
当Q(s)≈1时,式(2)、式(3)、式(4)分别为:
Guy(s)≈Gn(s),Gdy(s)≈0,Gξy(s)≈1
(6)
由式(1)和式(6)可知,系统模型在低频段与参考模型近似相等,起到抑制扰动的作用,但会引入测量噪声;扰动观测器在高频段不会对系统产生影响,更不会引入高频噪声[10].
2 基于扰动观测器的逆变器双闭环控制方案设计
2.1 双闭环控制方案设计
本文中电流内环的反馈电流以逆变器的输出电流作为反馈信号[11],逆变器的电压/电流双闭环控制器如图3所示.
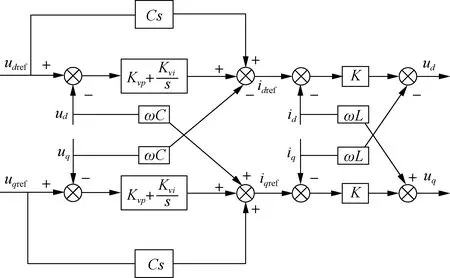
图3 逆变器双闭环控制器
电压外环的主要作用是为电流内环提供参考信号,改善电压质量.电压外环的方程表达式为:
(7)
式中,Kvp和Kvi分别为电压的比例和积分控制系数.
为了保证电流内环跟踪参考值的快速性,采用控制器系数为K的比例控制器,改善系统的动态性能.电流内环的方程表达式为:
(8)

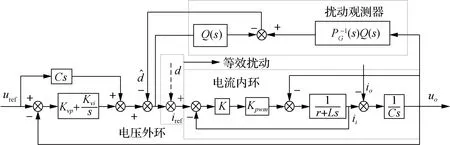
图4 加入扰动观测器后的电压控制框图
电流环的闭环传递函数Pin(s)和输入、输出的传递函数PG(s)为:
(9)
(10)
式中,Kpwm为逆变器电压增益,其值为直流电压源幅值的一半.
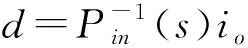
由于系统传递函数PG是二阶最小相位系统,低通滤波器的阶数应大于等于被控对象的阶数,选取Q(s)=1/(τs+1)2,τ为时间常数,扰动观测器的等效方程式可以表示为:
(11)
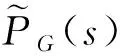
电压外环采用PI控制器C(s)=Kvp+Kvi/s,Kvp、Kvi分别为电压外环的比例和积分系数.图4中未加扰动观测器时,系统输出的传递函数为:
uo=φr(s)uref+φd(s)d
(12)
(13)
(14)
加入扰动观测器后,式(12)、式(13)、式(14)可改为:
(15)
(16)
(17)
当Q(s)接近1时,由式(15)—式(17)可得:
(18)
由式(18)可以看出,即使扰动模型存在,也会被强制为没有扰动的标称模型,这个现象叫做标称特性,能明显改善系统参数不确定时的鲁棒性.
2.2 参数整定
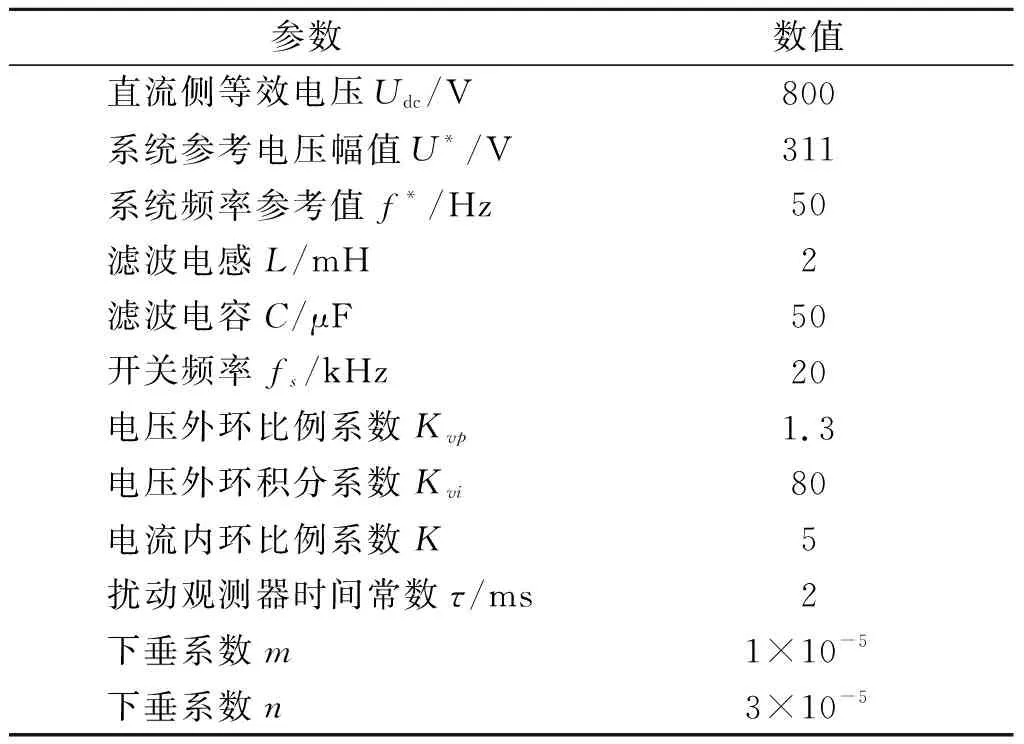
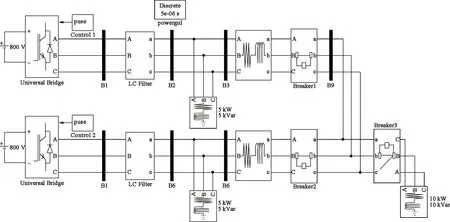
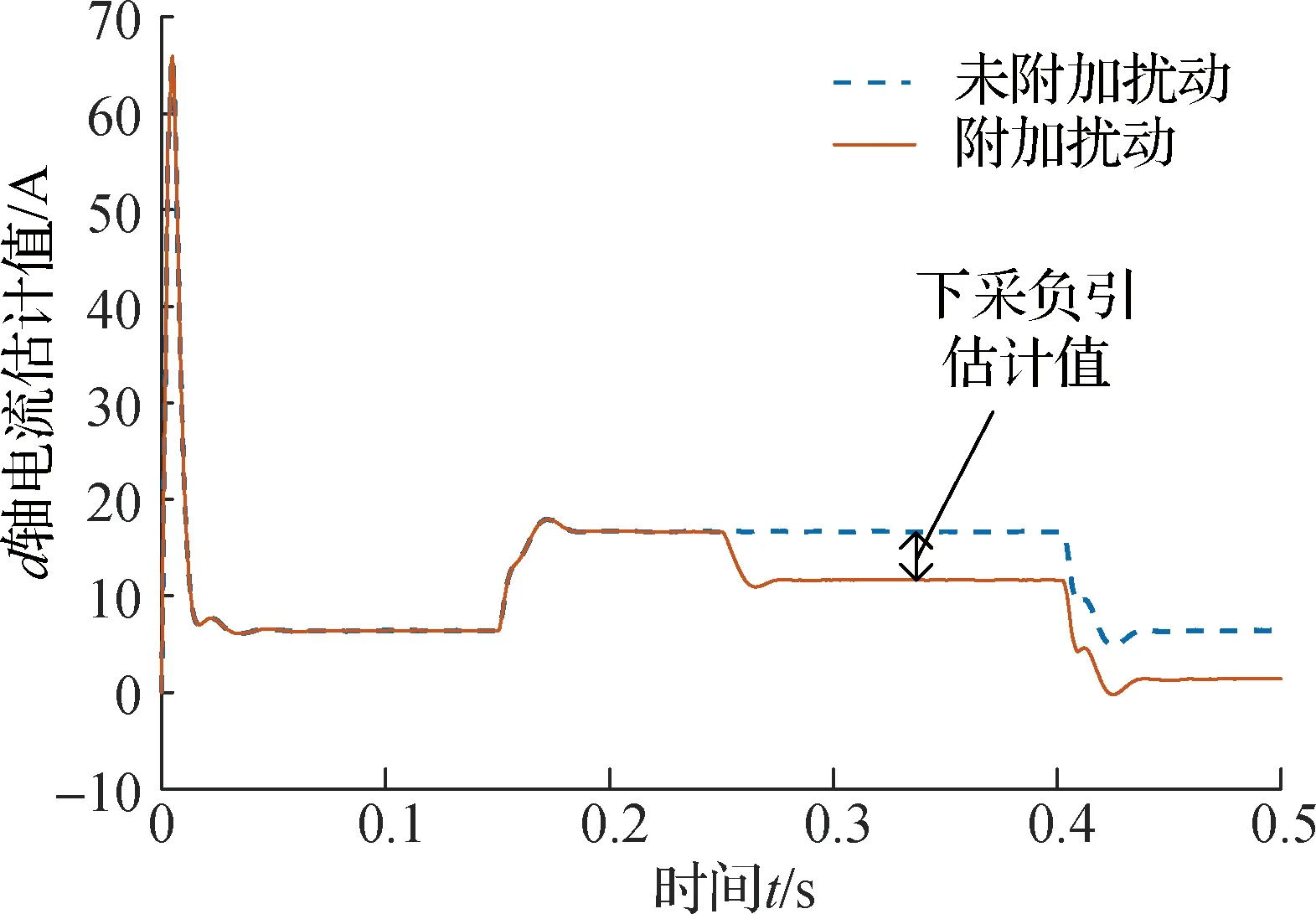
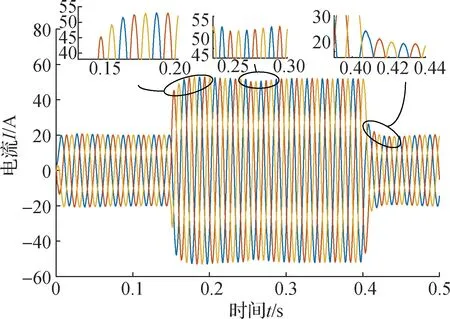
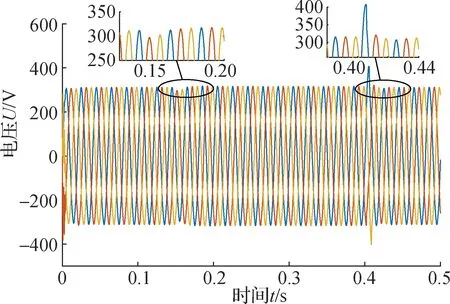
滤波器设计最主要部分是时间常数的设计,时间常数τ应满足两个条件[12]:1) 保证截止频率大于外部扰动角频率,即ωb>ωd,ωd为外部扰动的角频率;2)保证截止频率小于噪声频率和系统约束角频率中的最小值,即ωb (19) 对于本节所提整数阶干扰观测器Q(s)=1/(τs+1)2,其截止频率为: (20) 将式(20)代入式(19)得τ的范围为: (21) 将负载电流视为系统的扰动,稳态时角频率ωd=0,取ωs=ωc;由于噪声扰动的复杂性以及不确定性,在参数计算时暂不考虑噪声的扰动. 图5为滤波器时间常数取不同值时电压开环传递函数的Bode图,和未加DOB时相比,加入DOB后的低频段幅值变大,电压跟踪能力在低频段更好;高频段曲线在加入DOB前后都是重合的,表明高频段的性能不受DOB加入的影响.综合考虑,最终取τ=2 ms. 图5 电压开环传递函数Bode图 实际被控对象模型在有参数摄动或是外部干扰存在的情况下,其乘性摄动形式可表示为: (22) 式中:W(s)为参数摄动的不确定度;Δ(s)为可变参数. W(s)可以进一步表示为: (23) 假设W(s)、Δ(s)的上限已知且稳定,则系统鲁棒稳定的充要条件为[5]: (24) 式中,K(s)为等效控制器的传递函数. 在未加DOB时,K(s)=C(s);加入DOB后,K(s)可以表示为: (25) 式(24)可以进一步写成: (26) 将未加DOB时的K(s)和加入DOB后的K(s)分别代入式(26),可以得到不同鲁棒性能的权重. 图6为DOB加入前后系统鲁棒性能的比较图,由图6可见,在低频段和中频段,加入DOB后的鲁棒性能高于未加DOB时的情况;在高频段,两种情况下的曲线趋于重合,鲁棒性能相同. 图6 有无DOB的鲁棒性能比较图 由于等效扰动作用于电压外环,其主要受电容参数摄动的影响,所以有必要分析电容参数摄动情况下系统的稳定性.首先求出系统传递函数对电容参数摄动的灵敏度,然后根据灵敏度的大小判断其稳定性. 1)φr(s)对于C的灵敏度.不加DOB时,输出电压关于参考电压的传递函数φr(s)对电容参数C的灵敏度为[8]: (27) (28) 2)φd(s)对于C的灵敏度.不加DOB时,输出电压关于扰动电流的传递函数φd(s)对电容参数C的灵敏度为: (29) (30) 图7 φr(s)对C摄动的灵敏度Bode图 图8 φd(s)对C摄动的灵敏度Bode图 由以上分析可知,DOB的加入能有效抑制外部扰动和参数摄动带来的不利影响,间接表明了DOB的加入对系统稳定性起积极作用. 为了验证本文方法的控制效果,搭建Simulink逆变器并联模型,以2台逆变器为例.设置运行时间0~0.15 s,两逆变器并联运行,但只带本地负载运行;在0.15 s时合上开关,公共端接上负载,逆变器1和逆变器2共同为负载提供能量;在0.4 s时切除公共端的负载.系统参数设置如表1所示. 表1 系统参数设置 图9为逆变器并联系统的仿真模型图.由于本研究基于交流微电网,因此逆变器的直流侧输入端用一个800 V电压源等效.逆变器的控制模块主要包括功率计算模块、电压/电流双闭环模块和下垂控制模块三大模块. 图9 逆变器并联系统仿真模型 在仿真实施中,引入负载电流扰动和参数扰动两种扰动源,扰动观测器的作用就是估计出扰动量并进行补偿. 为了更好体现仿真效果,0.25 s时在电压/电流双闭环中加入1个幅值为5的扰动量,图10为外加扰动前后扰动观测器的观测值.从图10中可以看到,扰动观测器能准确观测扰动量的幅值大小,表明了扰动观测器的有效性. 图10 外加扰动前后DOB的观测值 图11为加入DOB前后电流d轴分量对比图.从图11中可以看到,在0.150 s投入负载时,未加DOB的情况下电流达到稳态需要0.060 s,而加入DOB后,只需0.030 s就能达到稳态;切除负载时,未加DOB的情况下电流达到稳态需要0.050 s,加入DOB后只需0.035 s;在外加扰动时,电流达到稳态的时间在加入DOB前后也相差了0.015 s.通过加入扰动观测器对负载扰动的前馈补偿,大大缩短了电流的波动时间,提高了系统的暂态稳定性. 图11 加入DOB前后d轴电流分量对比 图12为加入DOB前后电流的仿真波形图.从图12中可以看到,未加DOB时,负载的投切所产生的电流波动需要经过5个振荡周期才能完全消除,而外加的扰动则需要4个振荡周期才能消除;加入DOB后,负载投切所产生的波动仅需3个振荡周期就可以完全消除,而外加的扰动也仅需2个振荡周期就能消除.仿真波形表明,采用本文所提的扰动观测器可以有效减小负载投切带来的电流扰动,体现出良好的稳态性能. (a) 未加DOB 负载电流的扰动不仅会影响电流的波形,也会影响电压的波形,图13为加入DOB前后dq轴输出电压分量.从图13中可以看到,加入DOB后,电压的超调量比未加DOB时的超调量小,且大大缩短了恢复到稳态的时间. 图13 dq轴电压分量 图14为加入DOB前后电压的仿真波形图.由图14可见,未加DOB时,负载的投切引起了电压的扰动,电压恢复到稳定状态需要经历3个振荡周期;加入DOB后,负载投切引起的电压扰动只需经历2个振荡周期就能消除. (a) 未加DOB 电压和电流波形在加入DOB前后都有所不同,这直接导致功率在加入DOB前后也有所不同.图15为加入DOB前后逆变器输出的有功功率波形图.从图15中可以明显看出,未加入DOB时,功率的波形曲线波动较大且超调量也较大,波形曲线不够平顺;加入DOB后,由于负载扰动造成的超调量有效减小,曲线变得平顺,稳定性得到明显改善. 图15 加入DOB前后有功功率波形图 本文在逆变器并联系统双闭环的控制基础上,加入了扰动观测器以减小负载投切时带来的电压、电流波动和改善电能质量.从功率平衡的角度出发,并联系统中本地负载的扰动可以被最大化抑制或消纳在本地逆变器,从而减小逆变器间的功率波动.同时,本文给出的参数整定和稳定性分析方法可以大大减小扰动观测器参数确定时的工作量.仿真结果表明:本文所提方法准确性好,能正确估计扰动量的大小;快速性好,能实时追踪和反馈扰动量的大小;算法简单,易于移植;适应性好,有利于该方法的推广.
3 稳定性分析
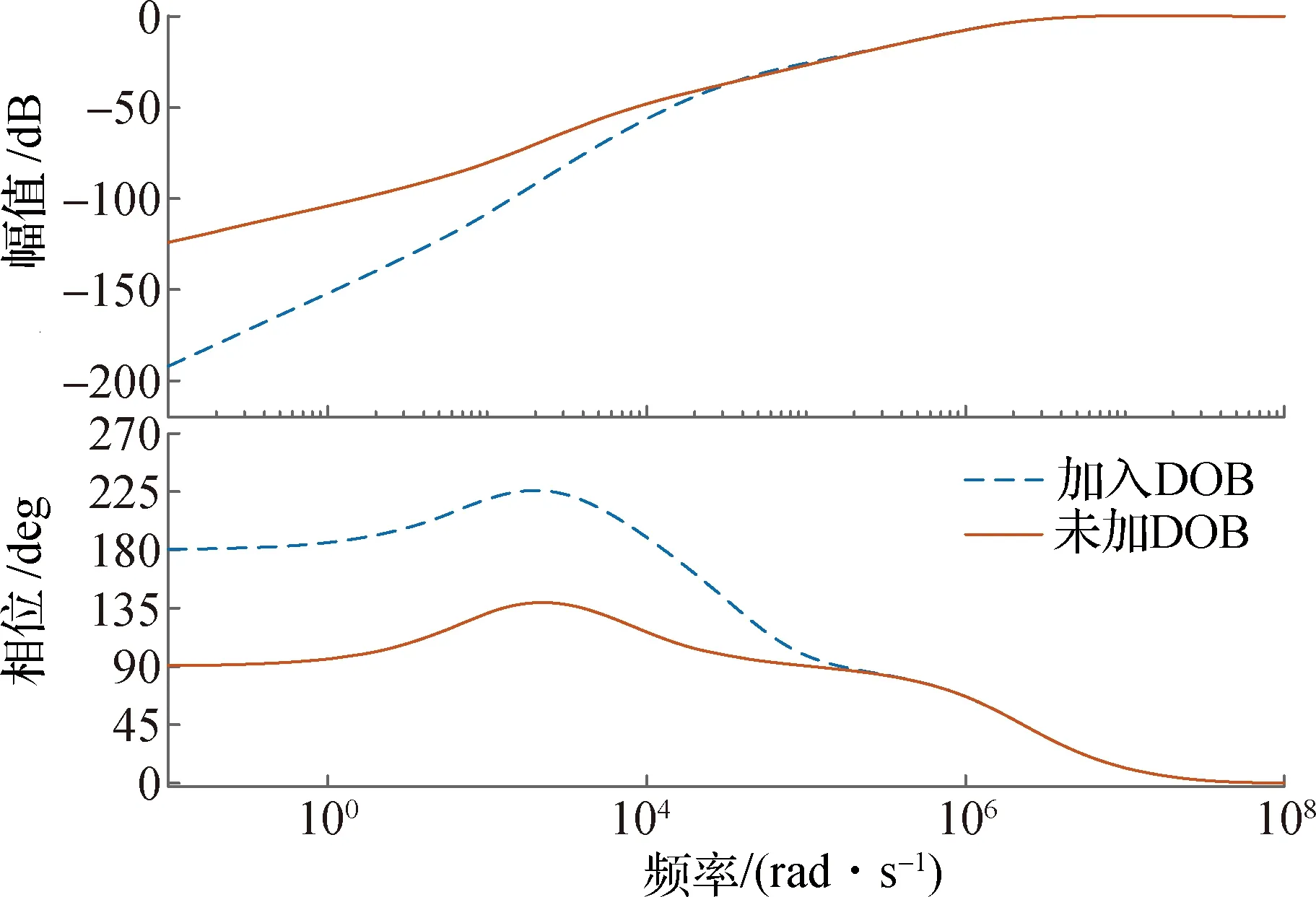
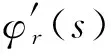
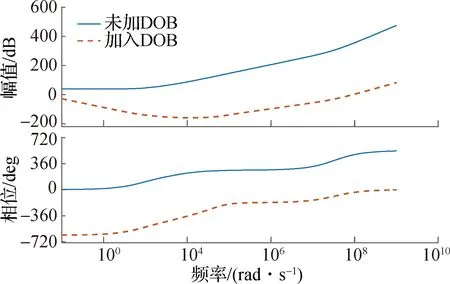

4 Matlab仿真分析
4.1 仿真模型的搭建
4.2 负载扰动的仿真分析



5 结语

