混沌鲸鱼优化算法及其在有限元模型修正中的应用
赵 宇,彭珍瑞
(兰州交通大学 机电工程学院,兰州 730070)
鲸鱼优化算法(whale optimization algorithm,WOA)是近年来提出的基于种群的启发式优化算法[1].WOA模拟座头鲸捕食,将其群体狩猎行为转化为随机优化过程.目前,WOA已成功应用于优化调度[2-3]、优化设计[4-5]、盲信号提取[6]、图像分割[7]等领域.但是WOA依然存在全局和局部搜索难以协调、易陷入局部最优等问题.
混沌优化算法因其利用混沌所具备的初值敏感性、伪随机性、遍历性等非线性动力学特征而广泛用于工程全局优化设计中[8].文献[9]使用分段Logistic映射对WOA的种群初始化,以保持种群多样性.文献[10]利用混沌映射调整WOA中的更新概率.文献[11]采用Tent映射反向学习初始化、最优个体混沌搜索等策略优化鲸鱼算法.
本文提出了一种基于混沌映射调整惯性权重的鲸鱼优化算法(whale optimization algorithm with chaotic maps,CWOA),分别利用5种混沌映射扰动惯性权重以协调算法全局探索和局部开发能力,并通过6个测试函数进行仿真实验,将加入混沌映射的CWOA与基本WOA比较,验证CWOA的有效性.最后利用Gauss映射的CWOA求解有限元模型修正问题,并将结果与遗传算法(genetic algorithm,GA)、粒子群算法(particle swarm optimization,PSO)进行对比.
1 鲸鱼优化算法
在搜索空间,“搜索代理”即每一头座头鲸都可以看作是优化问题的候选解.WOA通过猎物包围、Bubble-net狩猎及猎物搜索等行为更新搜索代理位置捕获猎物.
1) 猎物包围
假定当前最优解位置是目标猎物,其他搜索代理通过如下公式更新位置:
X(t+1)=X*(t)-A·D,
(1)
D=|C·X*(t)-X(t)|.
(2)
其中:A=2a·r-a,a=2-2(t/tmax),r是介于0~1之间的随机向量,t、tmax分别表示当前迭代次数、算法最大迭代次数;C=2·r;D是距离向量;X*(t)、X(t)分别表示目前最优解位置向量、当前位置向量.
2) Bubble-net狩猎
搜索代理会通过更新概率p在收缩包围机制或螺旋模型中做出选择来更新位置,公式如下:
(3)
其中:D′=|X*(t)-X(t)|表示搜索代理与目标猎物之间的距离;b是对数螺旋线形状常数;l是介于-1~1之间的随机数;p是介于0~1之间的随机数.
3) 猎物搜索
搜索代理可通过随机游走更新位置来增强算法全局探索能力,公式如下:
X(t+1)=Xr(t)-A·D,
(4)
D=|C·Xr(t)-X(t)|.
(5)
其中,Xr(t)是从种群中随机选择的搜索代理位置向量.
2 混沌鲸鱼优化算法
2.1 混沌映射
混沌映射产生的混沌序列使搜索代理位置遍历整个搜索空间,保证种群多样性,可用于提升基本WOA算法的全局搜索能力,避免其早熟收敛.本文采用Circle、Gauss、Logistic、Sinusoidal及Tent这5种混沌映射产生混沌序列,混沌映射见表1.考虑到混沌初值敏感性,为了便于比较,除Tent映射的初值为0.6外,其余映射初值均为0.7,映射的范围为(0,1),映射迭代100次.5种混沌映射如图1所示.
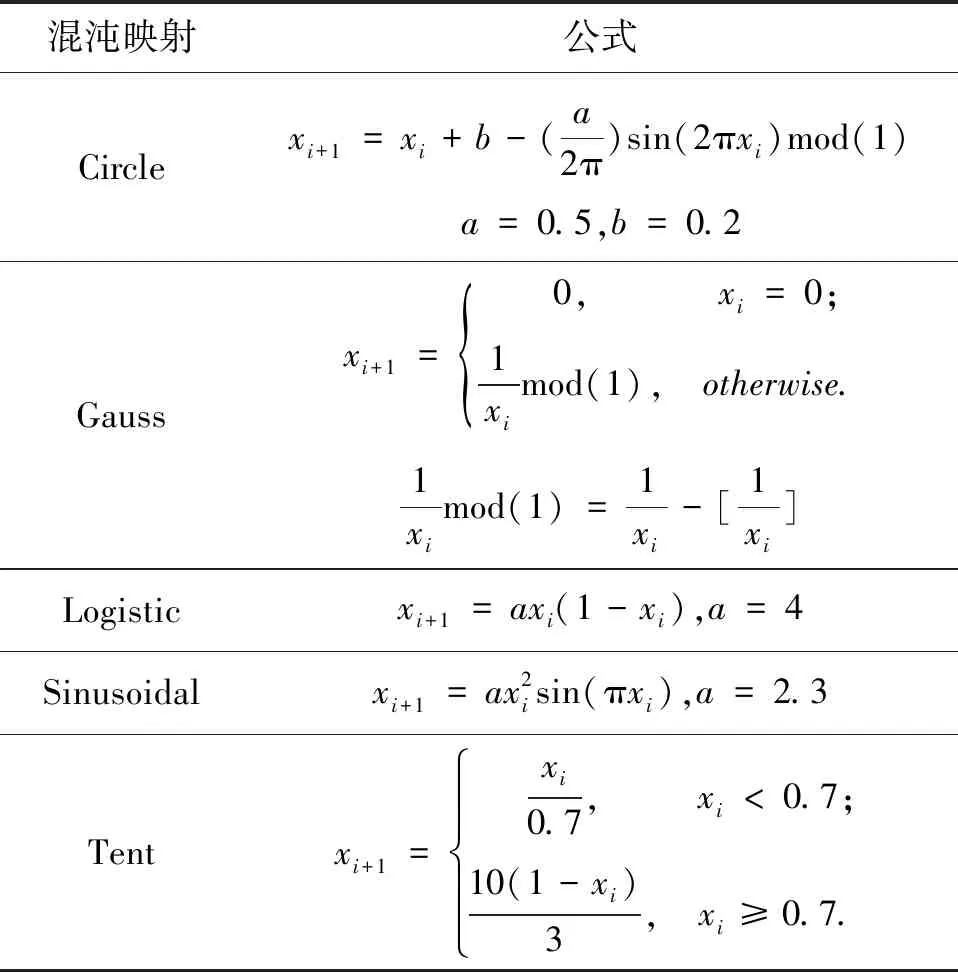
表1 混沌映射
2.2 混沌鲸鱼优化算法
为更好地协调算法的全局和局部的探索开发能力,引入带混沌扰动的惯性权重位置更新策略.惯性权重公式为
(6)
其中:ωi、ωf分别是惯性权重ω的初值、终值;chaos(t)是混沌序列.则当前位置和螺旋机制位置更新公式可表示为:
X(t+1)=ω·X*(t)-A·D,p<0.5;
(7)
X(t+1)=D′·ebl·cos(2πl)+ω·X*(t),p≥0.5.
(8)
CWOA在更新代理模型位置时,通过参数p和A,根据式(7)、(8)和式(4)选择不同的位置更新方式,具体CWOA的算法步骤如下:
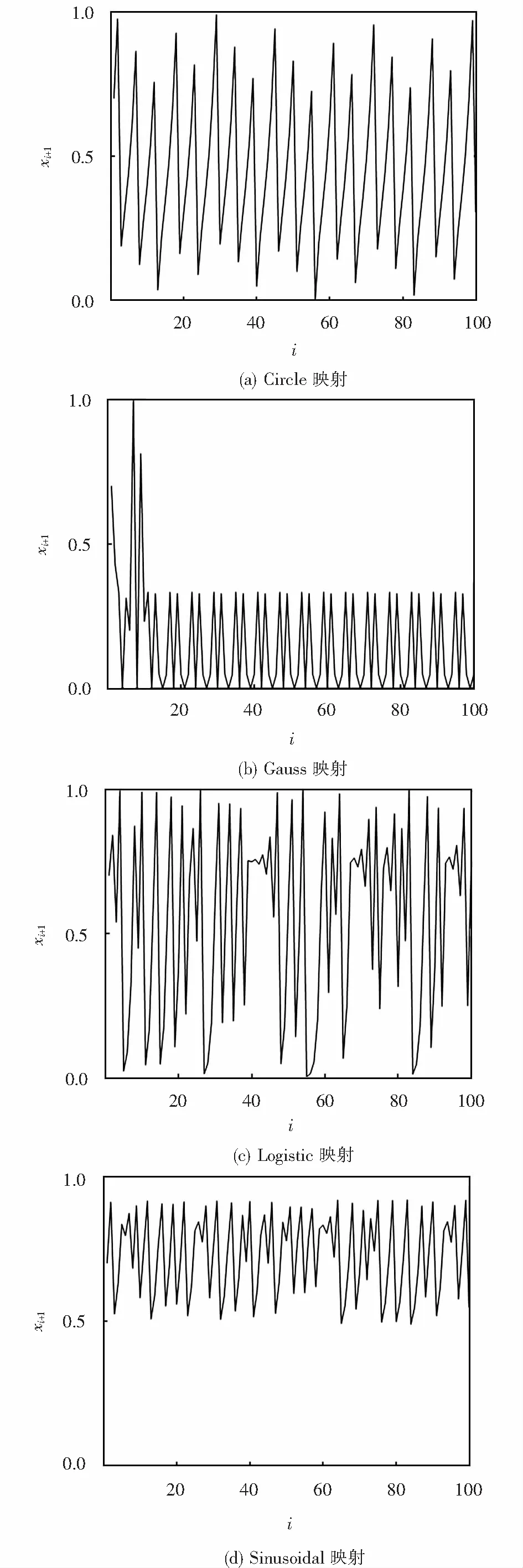
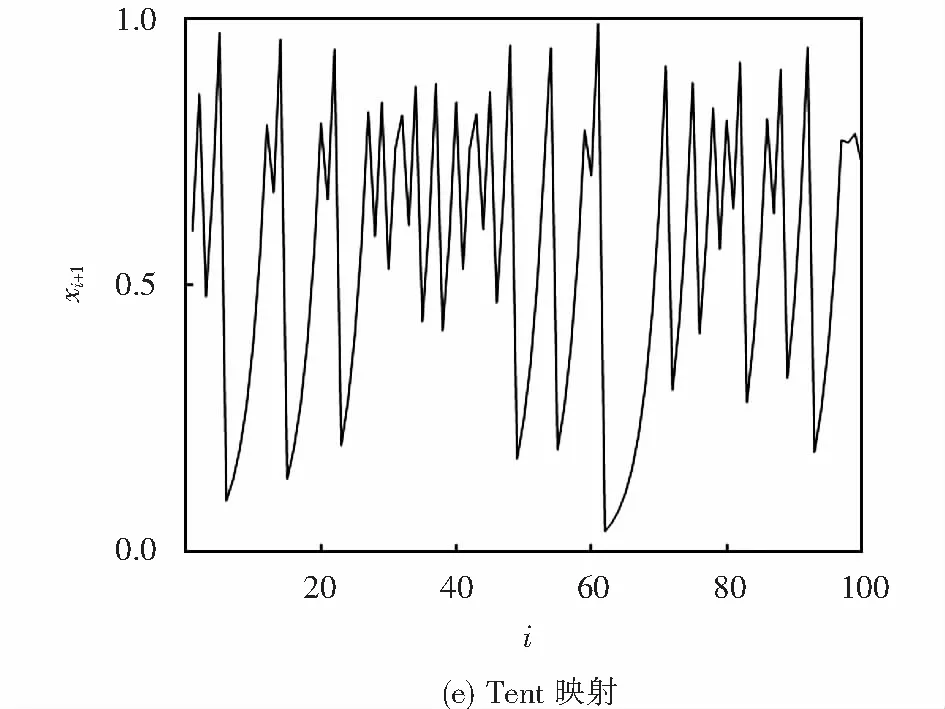
图1 混沌映射图Fig.1 Graphs of chaotic maps
初始化鲸鱼种群N,计算得出搜索代理的适应度值,记录当前最优个体X*;
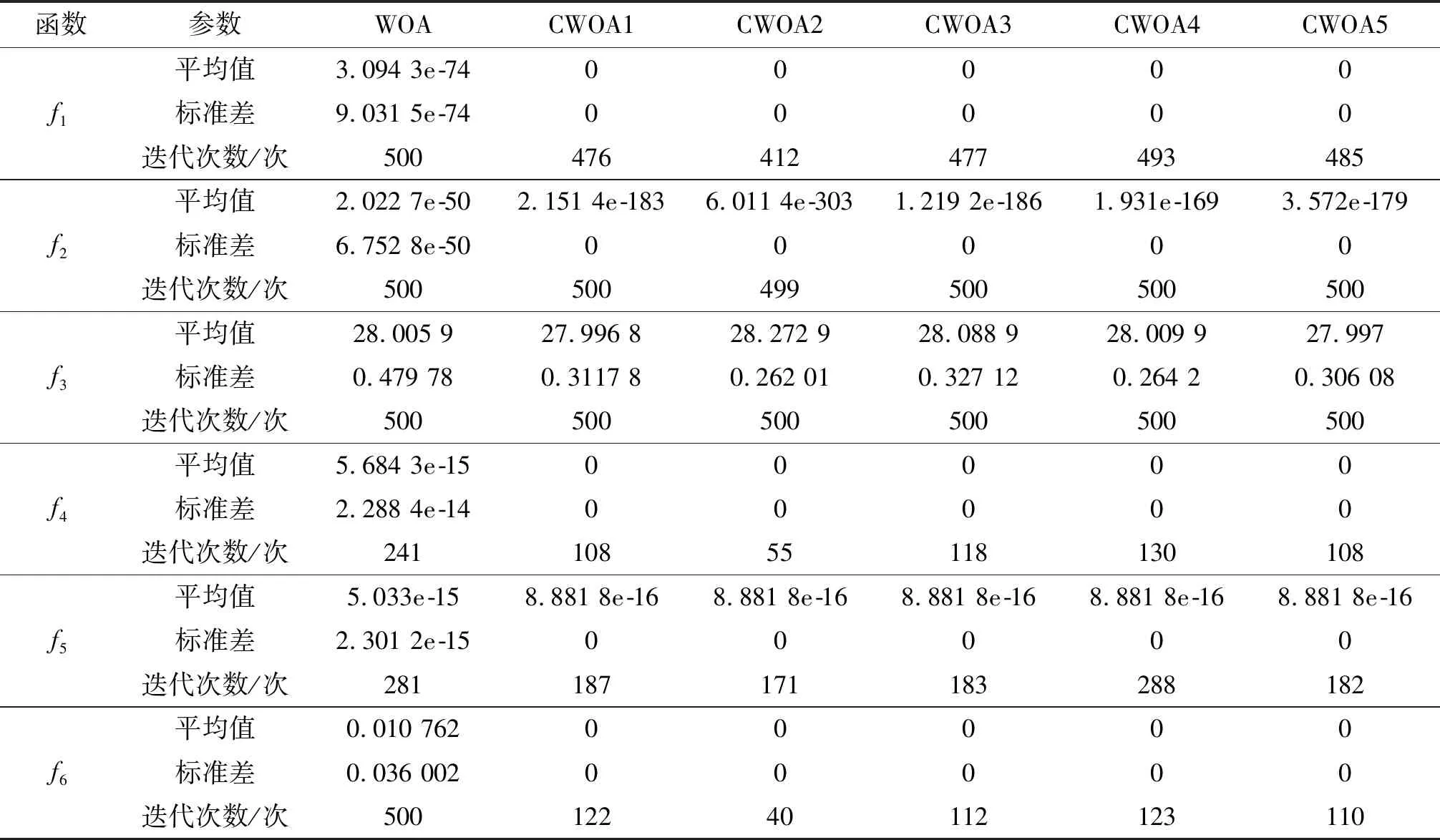
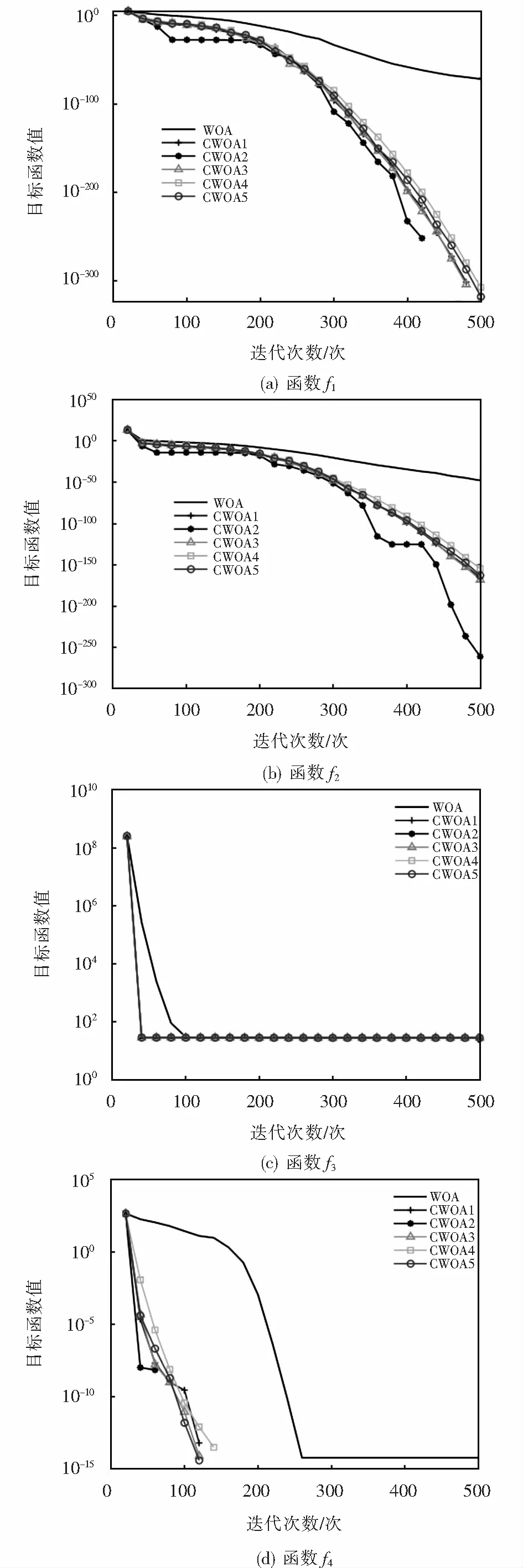
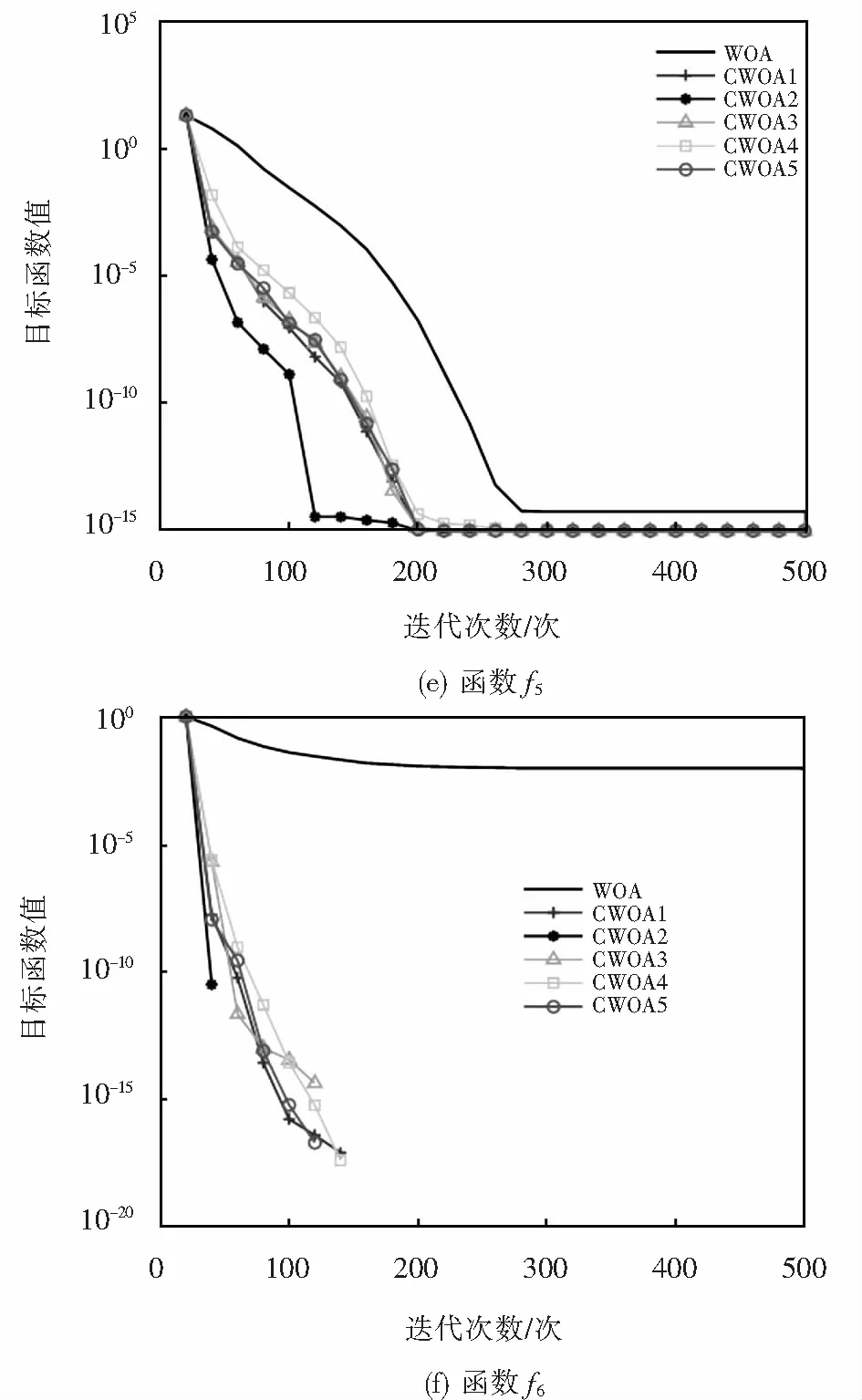
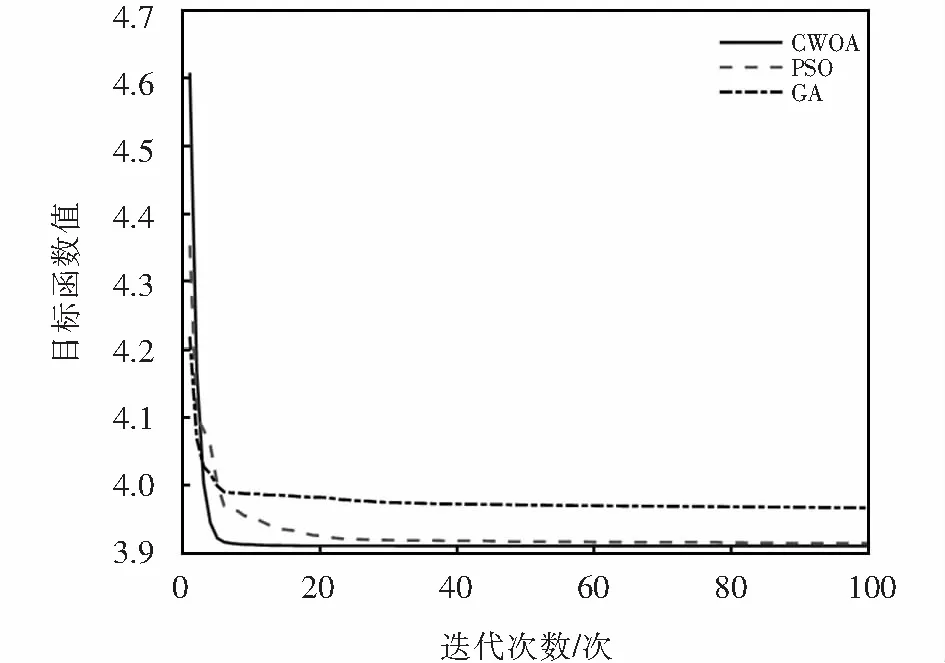
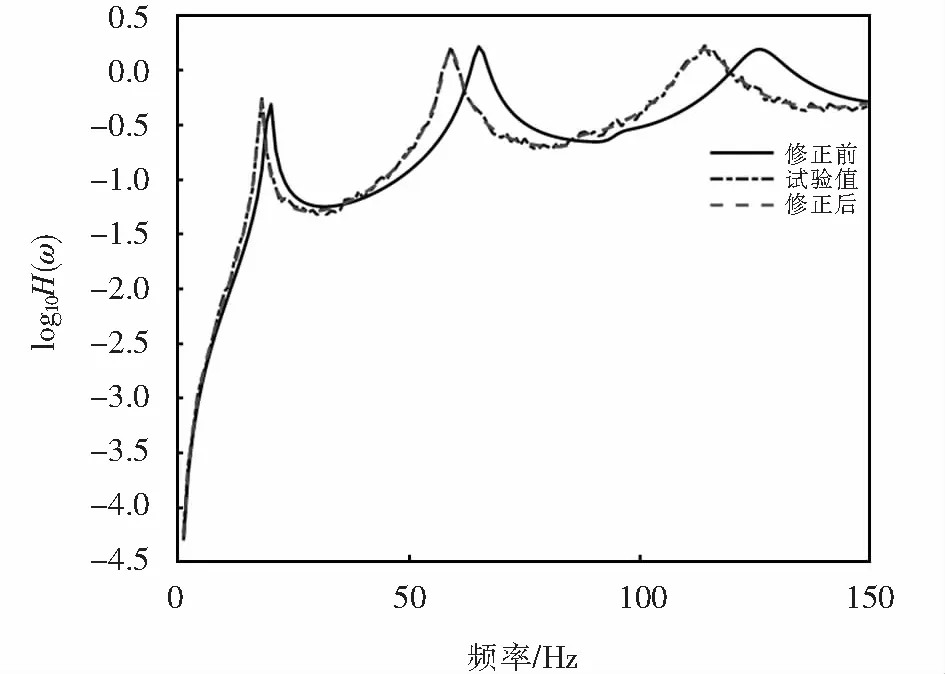
while(t fori=1∶N 更新参数a,A,C,l,p; if(p<0.5) if(|A|<1) 根据式(7)更新搜索代理位置; elseif(|A|≥1) 随机选择搜索代理位置Xr; 根据式(4)更新搜索代理位置; endif elseif(p≥0.5) 根据式(8)更新搜索代理位置; endif endfor 计算得出搜索代理的适应度值; 更新当前最优位置X*; t=t+1 endwhile 返回X*. 本文选用6个典型的基准测试函数将表1中的几种混沌映射分别代入式(6)中调整惯性权重,更新搜索代理位置,以评价算法的整体性能.测试函数见表2,f1~f3为单峰函数,其余为多峰函数. 对基本WOA算法分别加入Circle、Gauss、Logistic、Sinusoidal及Tent映射,记为CWOA1~CWOA5.算法的基本参数设置:种群大小均设为30;算法最大迭代次数均设为500;测试函数的维度为30;惯性权重初值ωi、终值ωf分别取0.9、0.2.每种混沌算法独立运行30次,求出运行结果的平均值、标准差以及所需的迭代次数.表3给出了CWOA1~CWOA5和基本WOA对不同测试函数的寻优结果.寻优收敛曲线如图2所示,为了便于观察,收敛曲线纵轴取以10为底的指数形式. 表2 基准测试函数 表3 WOA和CWOA的寻优结果比较 分析表3中结果可知:与WOA相比,除了函数f3,CWOA在其他的测试函数上均能获得较好的寻优效果;在函数f1、f4、f5和f6中CWOA4(Sinusoidal映射)在几种算法中所需的平均迭代次数最多;对于函数f3,只有CWOA1(Circle映射)和CWOA5(Tent映射)较WOA表现出较好的寻优性能.总体上而言,加入混沌映射惯性权重后提高了算法的寻优速度和精度. 图2 寻优收敛曲线比较Fig.2 Comparisons of optimization convergence curves 从图2中可以看出,相较于基本WOA,虽然图2(c)中加入混沌策略的算法在函数f3的寻优过程中并未表现出优越的寻优性能,但是,CWOA算法在其他5个测试函数上均展现出了较优的收敛速度和寻优精度,尤其是CWOA2(Gauss映射)算法.图2(d)和(f)中,CWOA2分别在迭代55次和40次后就到达了理论最小值0.因此,将加入Gauss映射的CWOA用于有限元模型修正问题中. 有限元模型修正是通过调整模型中的设计参数使得模型的计算响应与结构实测响应差异最小,最终使得修正后的有限元模型能够更准确、可靠地反映实际结构特性,还可以为结构的健康监测状况评估提供依据,这是典型的优化问题[12-14].一般以固有频率、模态振型或频响函数等振动信息为目标,构造模型修正目标函数[15].由于频响函数含有较多的频率点信息,可以避免因模态识别带来的不必要的误差.本文使用加速度频响函数进行模型修正. 对于多自由度阻尼系统,其加速度频响函数为 (9) 式中:M、C、K分别为n×n维结构的质量矩阵、刚度矩阵、阻尼矩阵;ω为激励频率. 此时,可将有限元模型修正问题转化为目标函数最小化问题进行求解: (10) 其中:xi是第i个待修正参数;lb和ub分别是修正参数 的上限、下限;m是待修正参数个数;k是频率点个数;Ht(ωj)、Ha(ωj)分别是在第j个频率点ωj上的试验实测加速度频响函数值、有限元模型所得频响函数值. 为验证CWOA针对有限元模型修正问题的有效性,分别采用GA、PSO和加入Gauss映射的CWOA解决一二维桁架的有限元模型修正问题.桁架如图3所示,该桁架结构包含25个杆单元、14个节点.除节点1和节点13,其他节点有x、y两个方向的自由度,共25个自由度.杆单元的弹性模量为E=210 GPa,密度为ρ=7 850 kg·m-3. 图3 二维桁架Fig.3 Two-dimensional truss model 选取x=[E,ρ]即弹性模量和密度为待修正参数.假设上述模型弹性模量和密度为真实值,所对应加速度频响函数为试验实测值.并对弹性模量增加10%、密度减少10%得到有限元值.选取节点11的y方向为试验测试激励点,节点3的y方向为测试点.对于加速度频响函数,频率范围0~150 Hz.对实测频响加入5%的噪声,以模拟试验过程中噪声的影响.分别利用GA、PSO和CWOA求解式(10).求解时,所有算法种群大小和算法最大迭代次数取值相同,分别为50、100.其他参数设置见表4.求解过程的迭代收敛曲线如图4所示.修正结果对比见表5. 从图4可以明显看到,迭代求解过程中,与GA、PSO比较,CWOA算法显示出更好的计算结果,收敛速度快,计算精度高.由表5可以得出,加入Gauss映射的CWOA算法其修正后的误差更小,修正结果更接近试验值.CWOA对有限元模型修正问题有较好的求解精度. 图5给出了修正前后加速度频响函数对比曲线.由图5可以看到,修正后的频响函数与试验频响函数曲线有很好的重合,进一步验证了所提出的CWOA算法的修正效果. 表4 算法参数设置 图4 迭代收敛曲线对比Fig.4 Comparison of iterative convergence curves 表5 参数修正结果对比 图5 修正前后频响函数曲线Fig.5 Curves of frequency response function before and after model updating 对于基本WOA算法仍然存在的收敛精度不高、全局和局部搜索难平衡、易陷入局部最优解的问题,将带混沌扰动的惯性权重更新策略用于鲸鱼位置更新中,基于混沌策略提出了改进鲸鱼优化算法CWOA.通过5种混沌映射在基准测试函数中的对比,得出Gauss映射能更好的提高WOA的性能.并将加入Gauss映射的CWOA用于有限元模型修正问题求解中,验证了CWOA解决这一工程问题的有效性.3 仿真与分析
3.1 基准测试函数
3.2 结果对比分析

4 有限元模型修正问题
4.1 目标函数
4.2 基于CWOA的有限元模型修正



5 结论

