大尺度薄壁结构力-热-电一体化分析
何东泽,李彦斌,陈 强,刘 健,谭福颖,费庆国
(1. 东南大学江苏省空天机械装备工程研究中心,南京 211189;2. 东南大学机械工程学院,南京 211189;3. 北京空天技术研究所,北京 100074)
0 引 言
位于飞行器最前端的天线罩结构不仅承担着气动力载荷和气动热载荷,同时也承担着保护飞行器雷达制导系统等关键电子系统的重要任务。因此,天线罩需要同时满足力学性能和电磁学性能。但在结构设计过程中,由于力学参数和电磁学参数结合跨度较大等原因,导致天线罩的力学设计和电磁学设计是相互独立的设计流程,从而使得天线罩多物理场一体化分析的研究较为滞后。因此,开展天线罩力-热-电一体化分析方法研究具有重要的理论意义和工程应用价值。
计算电磁学发展初期大多采用由Harrington[1]提出的矩量法,该方法具有较高的计算精度,但其计算效率极低。针对这一问题,王永[2]提出了关于矩量法的多线程并行算法,虽然在一定程度上提高了矩量法的计算效率,但仍不能满足日益增长的工程计算需求。近年来发展的多层快速多级子方法[3-5]能够大幅提高电磁分析的计算效率。快速多极子算法是基于矩量法的快速算法,通过将等效电流源划分为若干小组,对远距离作用的电流组可以采用快速求解积分方法进行求解,极大程度上加快了电磁场求解过程中矩阵-向量乘法的计算过程。而继承快速多级子算法有效减少计算存储量和复杂度的多层快速多极子算法进一步大幅度的降低计算的存储量和复杂度,进而使得电磁计算效率有了较大的飞跃。因此,多层快速多极子算法也被广泛应用于大尺寸结构的电磁性能计算[6]。随着飞行器飞行速度以及天线罩尺寸的增加,天线罩电磁性能的仿真计算量也呈现指数性的增长。为进一步提高计算效率,研究人员相继提出了几何射线法[7-8]、物理光学法[9-10]等一系列高频算法,能够在保证相对精度的前提下,大幅度地提升电磁分析的计算效率。
随着新型飞行器飞行速度的不断增加,天线罩所承担的气动力和气动热载荷变得越来越严酷[11-13]。此外,在飞行器结构轻量化的发展需求下,天线罩结构的安全余量设计对其力学性能预示的精度提出了更高要求。因此,在飞行器的设计阶段要充分考虑气动力效应和气动热效应对结构安全性能的影响。Behnke等[14]针对气动热、气动力和气动噪声载荷下高速飞行器进行了多场耦合分析,并通过显式动力学和隐式动力学结果的对比证明了分析方法的准确性。文献[15-20]深入研究了气动热对飞行器结构各频段振动特性的影响。杨学军等[21]、周志坛等[22]深入研究了运载火箭的底部热环境,认为随着运载火箭飞行高度的增加,火箭底部热环境存在明显的变化。吴大方等[23]通过对轻质陶瓷和新型陶瓷、纳米材料复合结构开展1700 ℃的高温试验测试,认为陶瓷、纳米材料复合结构的热防护性能明显优于轻质陶瓷。
实际服役状态下的天线罩既承担着气动热载荷和气动力载荷,也承担着对于飞行器雷达等重要电子元器件的保护功能。因此,在天线罩设计过程中需要同时考虑结构的强度/刚度性能和电性能。由于力学变量和电磁学参数结合跨度较大,导致电磁学计算中通常不考虑结构的强度/刚度参数,力学强度/刚度分析中同样不考虑电磁学性能,这也使得天线罩多物理场一体化分析的研究较为滞后。在实际的工程设计中,力学和电磁学分析相对独立,设计同时满足强度/刚度性能以及具有优良电磁性能的天线罩需要进行漫长的迭代和修改,这严重影响了飞行器设计的进度和成本。
本文基于有限元-多层快速多级子方法(FEM-MLFMM)提出一种天线罩的力-热-电一体化分析方法。首先,从有限元-多层快速多级子方法出发,将气动力载荷和气动热载荷作用下天线罩结构变形以及电磁参数变化作为变量参数引入天线罩透波性能计算中,形成力-热-电一体化分析方法;进而,以平板为研究对象,结合电磁学等效四端口网络计算方法,验证一体化分析方法的准确性;最后,探究不同载荷工况下天线罩的透波性能,分析气动力、气动热对天线罩透波性能的影响。力-热-电一体化分析流程如图1所示。
1 力-热-电一体化分析方法
力-热-电一体化分析关键在于建立三场分析变量之间的传递关系。气动力的影响主要体现在结构变形上,气动热的影响主要体现在结构变形、相对介电常数和损耗角正切等参数上。在气动热载荷作用下,介质的相对介电常数和损耗角正切分别为εt和tanσt。天线罩在非均匀气动力、气动热载荷下的状态方程可以表示为:
[K+Kσ]X(T,p)=F
(1)
式中:K,Kσ分别为天线罩结构的原始刚度矩阵和热应力引起的刚度矩阵,X(T,p)为温度和气动力相关的位移响应矩阵,F为气动力载荷。T和p分别代表气动热载荷和气动力载荷。
由于天线振子较多且入射点距离天线较远,因此可将入射波等效成为平面波,即
(2)
(3)
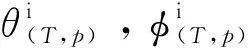
假设电磁波Hi(r(T,p)),Ei(r(T,p))照射到边界为S的均匀介质上,介质外的散射场可以等效为等效波源在均匀介质中产生的场,上述等效满足:
(4)
其中,M1和J1分别为分界面S上介质外的等效磁流和电流,E1和H1分别为分界面S上介质外的电场和磁场,n1为介质体内指向外的法向矢量。进一步可以写成:
-M1-n1×[Z1L1(J1)-K1(M1)]=n1×Ei
(5a)
(5b)
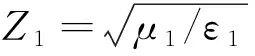
由于式(5a)和式(5b)相互等效,因此想要求出M1和J1还需要另外一个方程。此方程一般通过分界面内均匀介质中的电磁场得到。均匀介质内的场也可由边界S上的等效源表示:
(6)

进一步可以得到:
(7)
其中,Je为介质内电磁场的等效电流源。基于式(7),采用多层快速多极子的方法进行求解。等效电流源Je确定之后,远场分布计算方法为:
ES=Z2L2(Je)
(8)
式中:ES为天线罩外远场分布。
2 方法校验
为验证本文基于有限元-多层快速多级子的力热电一体化分析方法的准确性,以平板为研究对象开展一体化分析,并与等效四端口网络方法计算得到的功率传递系数解析解进行对比分析。
等效四端口网络方法作为相对成熟的等效平板理论,将电磁波和介质的相互作用简化为矩阵运算的形式,且经过长期的实际试验检验,具有较高的精度[24]。等效四端口网络可以分析多层结构的天线罩,如图2所示,其中εi,μi,di分别为第i层介质的相对介电常数、磁导率、厚度。
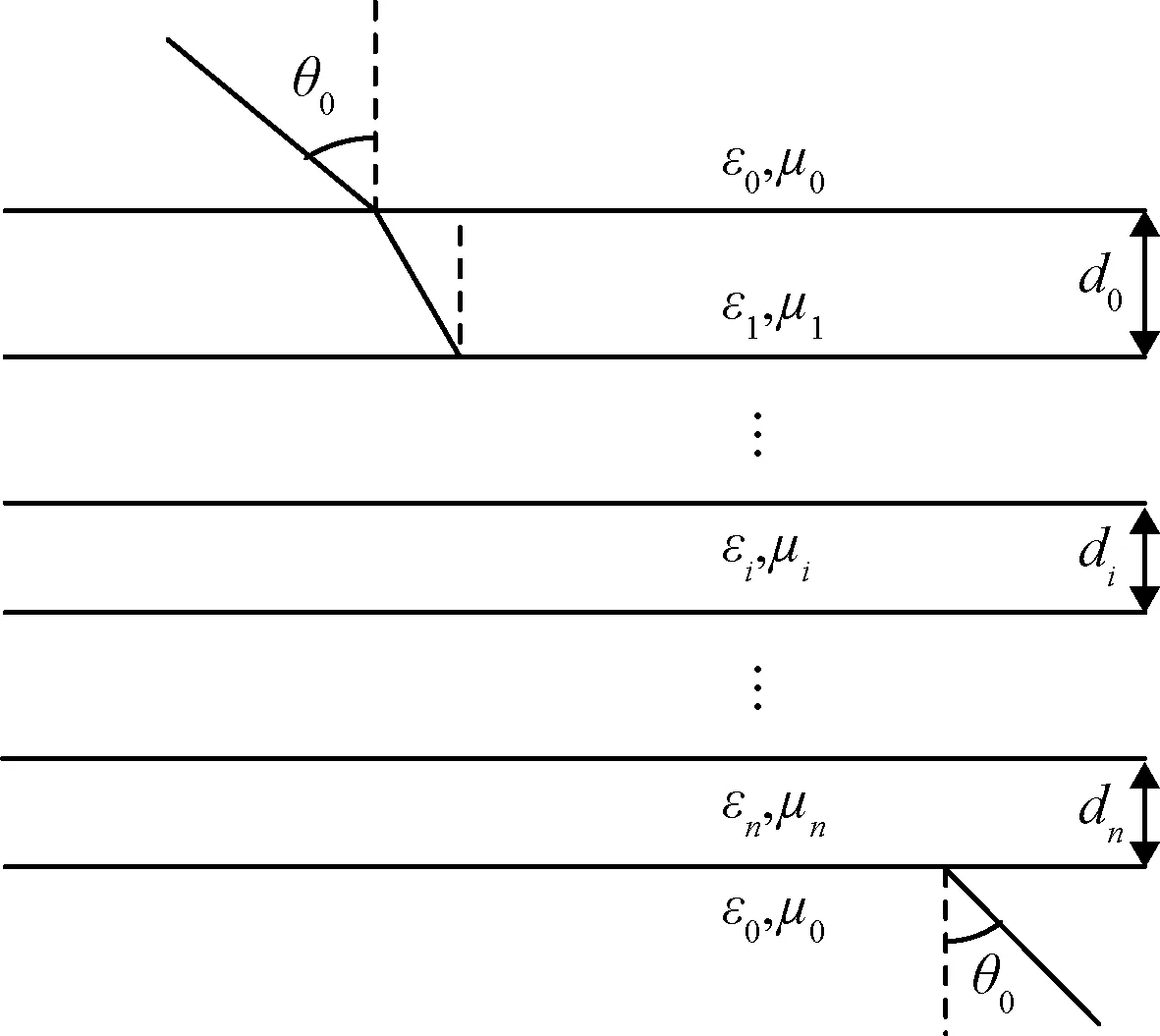
图2 多层平板电磁波传输示意图Fig.2 The transmission of electromagnetic wave in a multilayer plate
在气动热和气动力载荷共同作用下n级四端口网络,其网络总联矩阵Ttp为:
(9)

(10)

最终可得到在气动热和气动力载荷作用下的天线罩介质平板的传输系数Tsp为:
(11)
可得到天线罩在气动热和气动力载荷作用下的功率传输系数为:
Tspv=|Tsp|2
(12)
取激励频率f=3×109Hz;相对介电常数εr=3.62;损耗角正切tanσ=0.012;相对磁导率μr=1;入射角θ=63.5°;气动力载荷为均布面压,大小为0.5 MPa;气动热载荷为均匀温度场,大小为820 ℃;由式(12)可以计算得到平板在气动力、气动热载荷下的功率传输系数为77.41%。基于FEM-MLFMM的一体化分析方法可得平板的透波性能,计算结果如图3所示。由图3可知,天线的远场增益为16.39 dB,加入平板之后天线远场增益为15.08 dB,由式(10)可得原始透波率为73.94%,与理论解的误差为3.47%。误差来源主要有两方面:在等效四端口网络计算中将计算模型等效为理想无限大平板,相比多极子算法中的有限大的平板而言,会反射更多的能量,会使等效四端口网络计算的结果稍微下降;在等效四端口网络计算中将振子天线等效成理想平面波源,会使得实际的理论计算值明显偏大,这直接导致了理论计算的功率传输系数结果偏高。

图3 力、热载荷下天线罩平板透波性能曲线Fig.3 Transmittance curve of radome plate under temperature and pressure load
综上,本文提出的力热电一体化分析方法的结果误差合理,精度可靠。
3 天线罩力-热-电一体化分析
3.1 研究对象
以如图4所示的偶极子天线、图5所示的典型升力天线罩为研究对象,开展力-热-电多物理场下的一体化分析研究,探究气动力和气动热载荷对天线罩透波率的影响规律。天线罩力学材料参数如表1所示。

表1 天线罩材料参数Table 1 Material properties of radome
图4 天线振子示意图Fig.4 Schematic diagram of antenna oscillators

图5 天线罩有限元模型Fig.5 Finite element model of the antenna radome
相对介电常数也称为相对电容率,表征介质材料的介电性质或极化性质。介电损耗角正切[25]又称介质损耗角正切,表征电介质材料在施加电场后介质的能量损耗。天线罩材料的热导率和热膨胀系数、相对介电常数和损耗角正切随温度的变化曲线分别如图6、图7所示。

图6 天线罩材料热导率、热膨胀系数随温度变化曲线Fig.6 Heat conductivity and thermal expansion coefficient under different temperature

图7 天线罩材料介电常数和损耗角正切随温度变化曲线Fig.7 Dielectric constant and loss tangent under different temperature
仿真电磁波段为S波,中心频率3 GHz,标准波长为100 mm。天线阵子排布方式如图4所示,天线模型有多个垂直极化振子。主瓣方向为Z轴正方向。天线位于天线罩内部,距离天线罩后端面160 mm。天线的工作角度为-15°,采取天线主瓣方向保持不变,旋转天线罩的方式来模拟天线罩的实际工作角度。
3.2 载荷与边界条件
将气动力载荷简化为均匀面压载荷,即天线罩外表面均布大小为0.12 MPa的均匀面压。气动热载荷为如图8所示的非均匀温度载荷,最高温度位于天线罩最前端,温度为920 ℃,最低温度位于天线罩的尾部,温度为450 ℃。
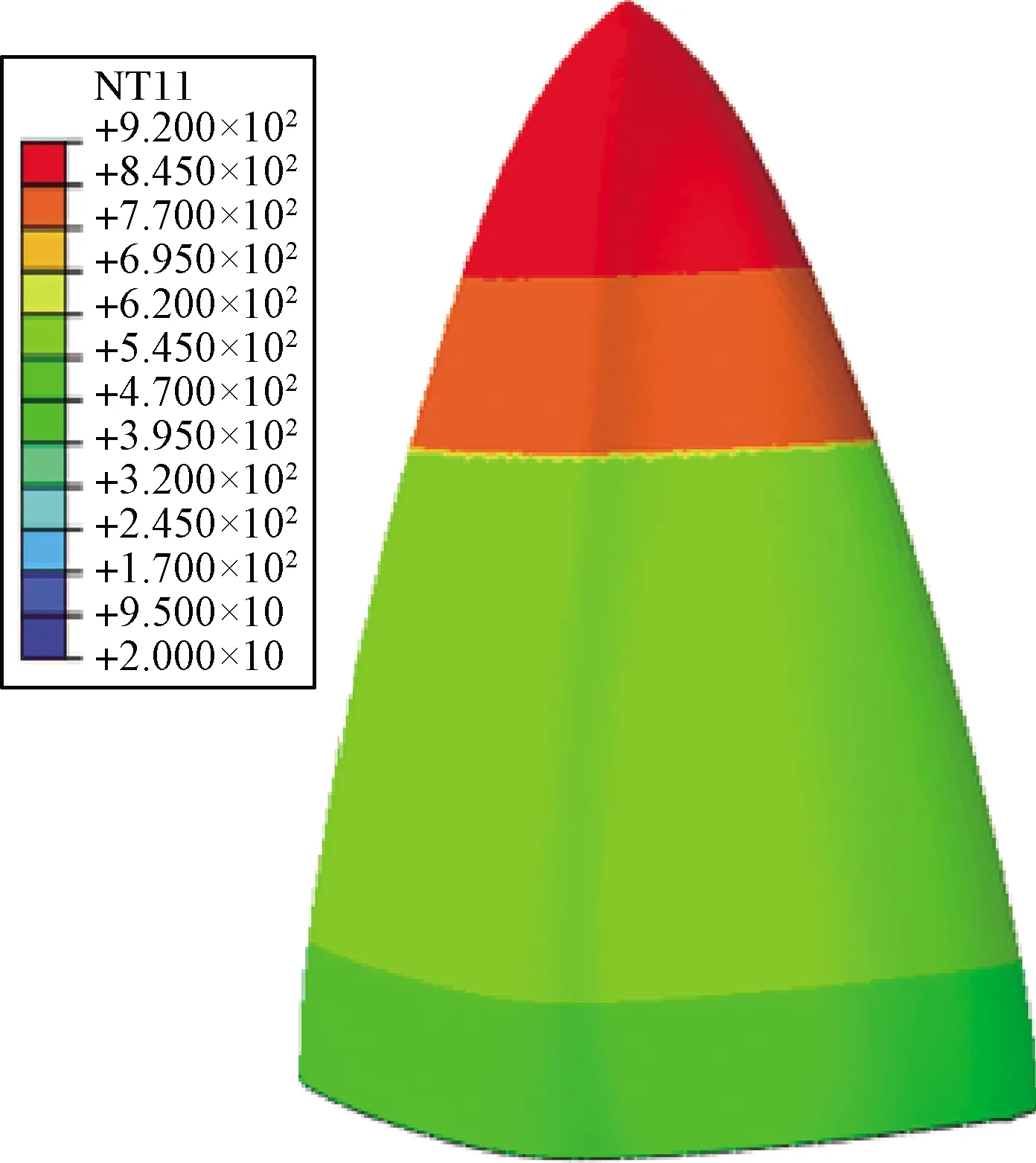
图8 气动热载荷下温度分布示意图Fig.8 Schematic diagram of aerodynamic heating load
4 力-热-电一体化分析
本节主要探究气动力载荷和气动热载荷对天线罩系统透波性能的影响。由于天线系统位于天线罩内部,不承担气动力和气动热载荷、天线振子均为金属材料且其材料参数均无明显变化,本节主要研究对象为天线罩结构,因此本文分别开展天线罩力-电耦合、热-电耦合、力-热-电耦合三种工况下的透波性能分析。
4.1 天线罩力-电耦合分析
气动力载荷下天线罩的位移和应力云图如图9所示,原始无载荷状态下天线的远场增益曲线如图10所示,气动力载荷状态下天线远场增益曲线如图11所示。结构最大变形为0.3 mm,位于距离天线罩最前端665 mm的底部平板上;最大应力为103 MPa,位于天线罩侧边处。
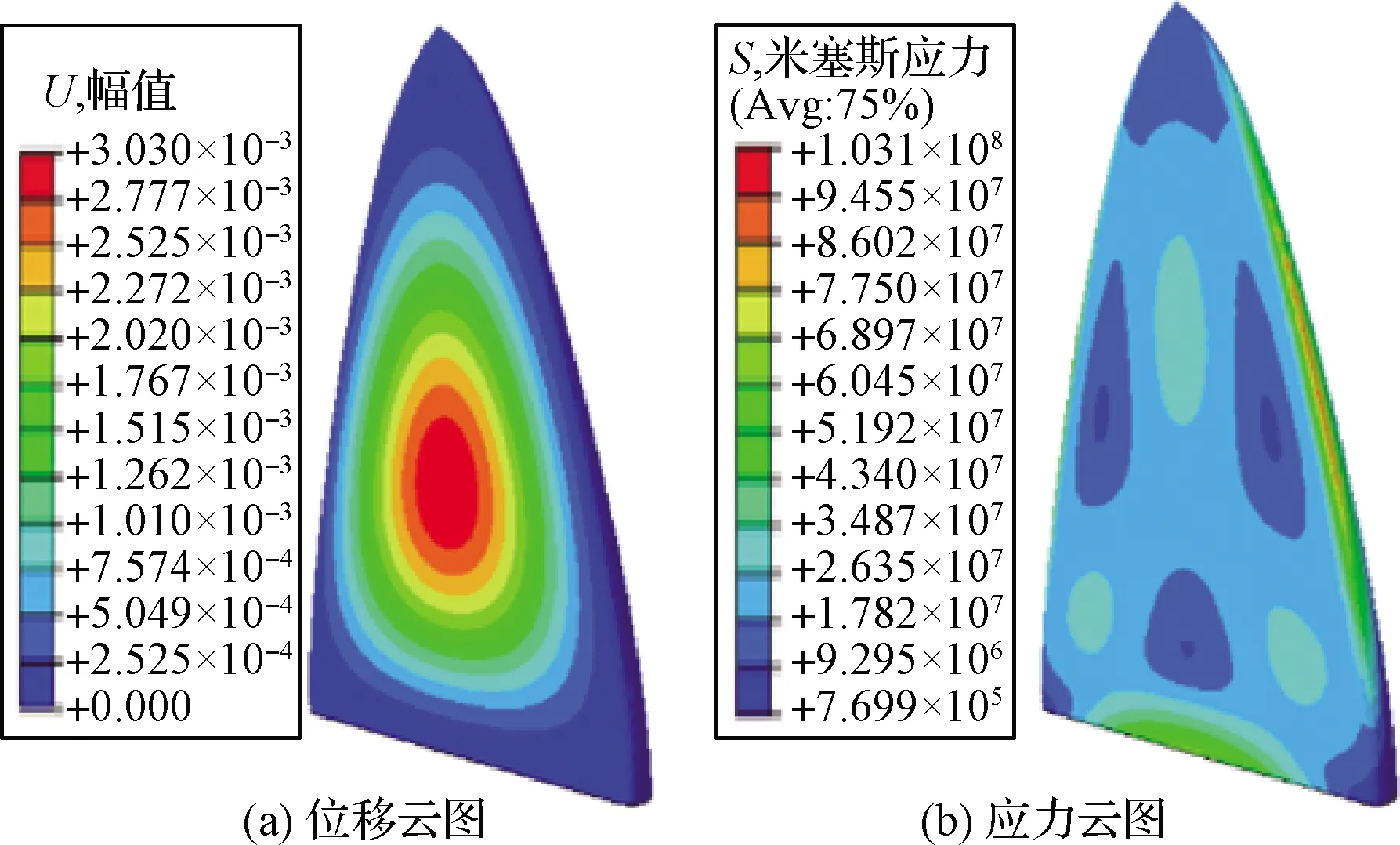
图9 力载荷下天线罩响应结果Fig.9 Response of radome under pressure load
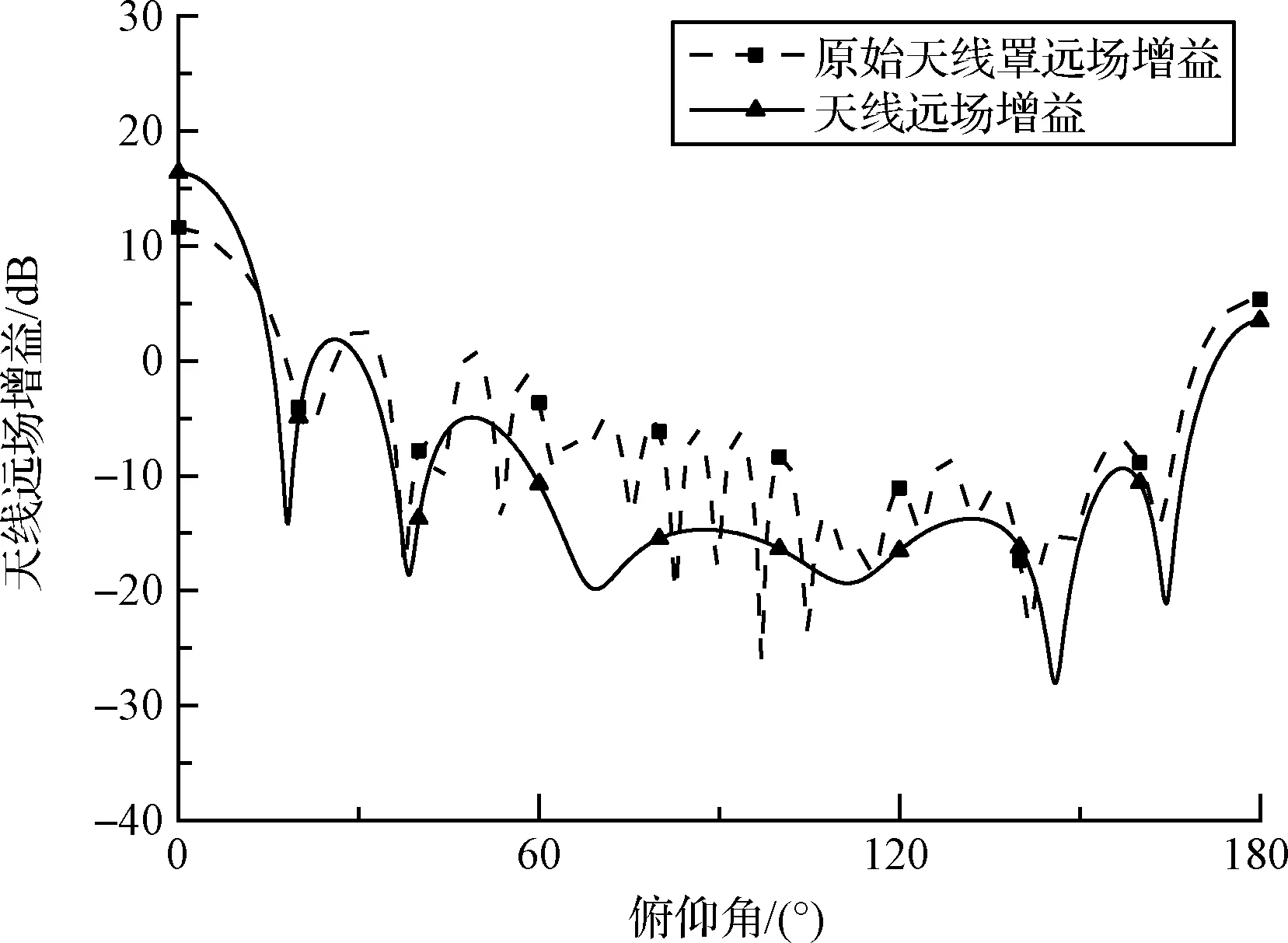
图10 天线罩透波性能曲线Fig.10 Transmittance curve of radome
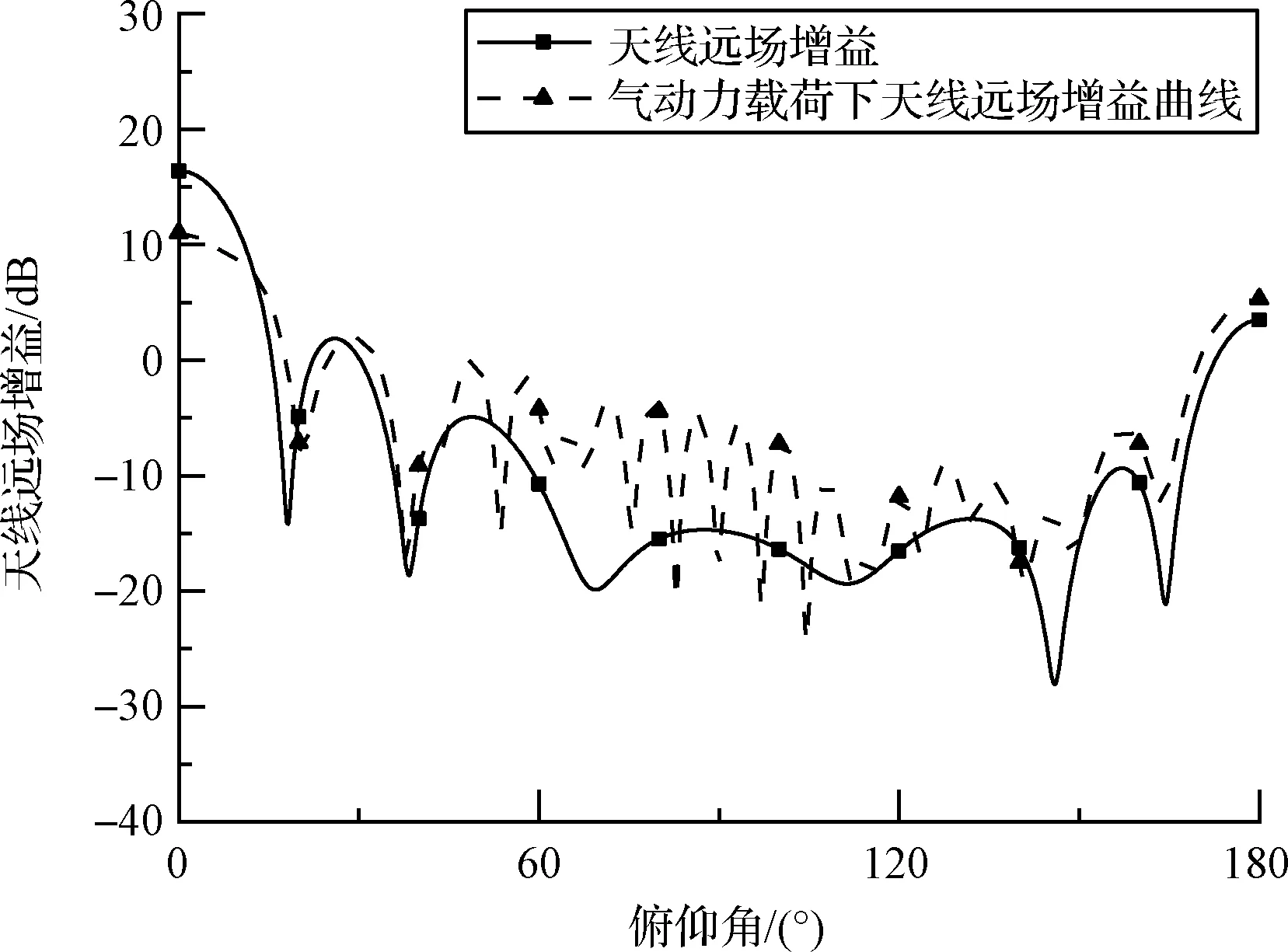
图11 力载荷下天线罩透波性能曲线Fig.11 Transmittance curve of radome under pressure load
原始状态为天线罩在没有变形时的状态,可为后续多种复杂物理场的一体化分析提供参照。由图10可知,天线的远场增益为16.39 dB,加入天线罩之后天线远场增益为11.61 dB,由式(10)可得原始透波率为33.31%。
由图11可知,气动力作用下天线罩远场增益为11.03 dB,透波率为29.10%,相比于原始状态,气动力下天线罩由于结构变形导致透波率下降1.93%。实际工程中,飞行器透波性能下降1.93%对于雷达系统的扫描和瞄准精度的影响是不可忽略的。因此,在前期设计阶段要充分考虑气动力载荷作用下天线远场增益下降的现象。
为探究气动力载荷对于天线罩透波性能的影响规律,本节分析了天线罩气动力载荷分别为0.12 MPa,0.17 MPa,0.22 MPa,0.27 MPa,0.32 MPa时天线罩的透波性能。分析结果如图12所示。
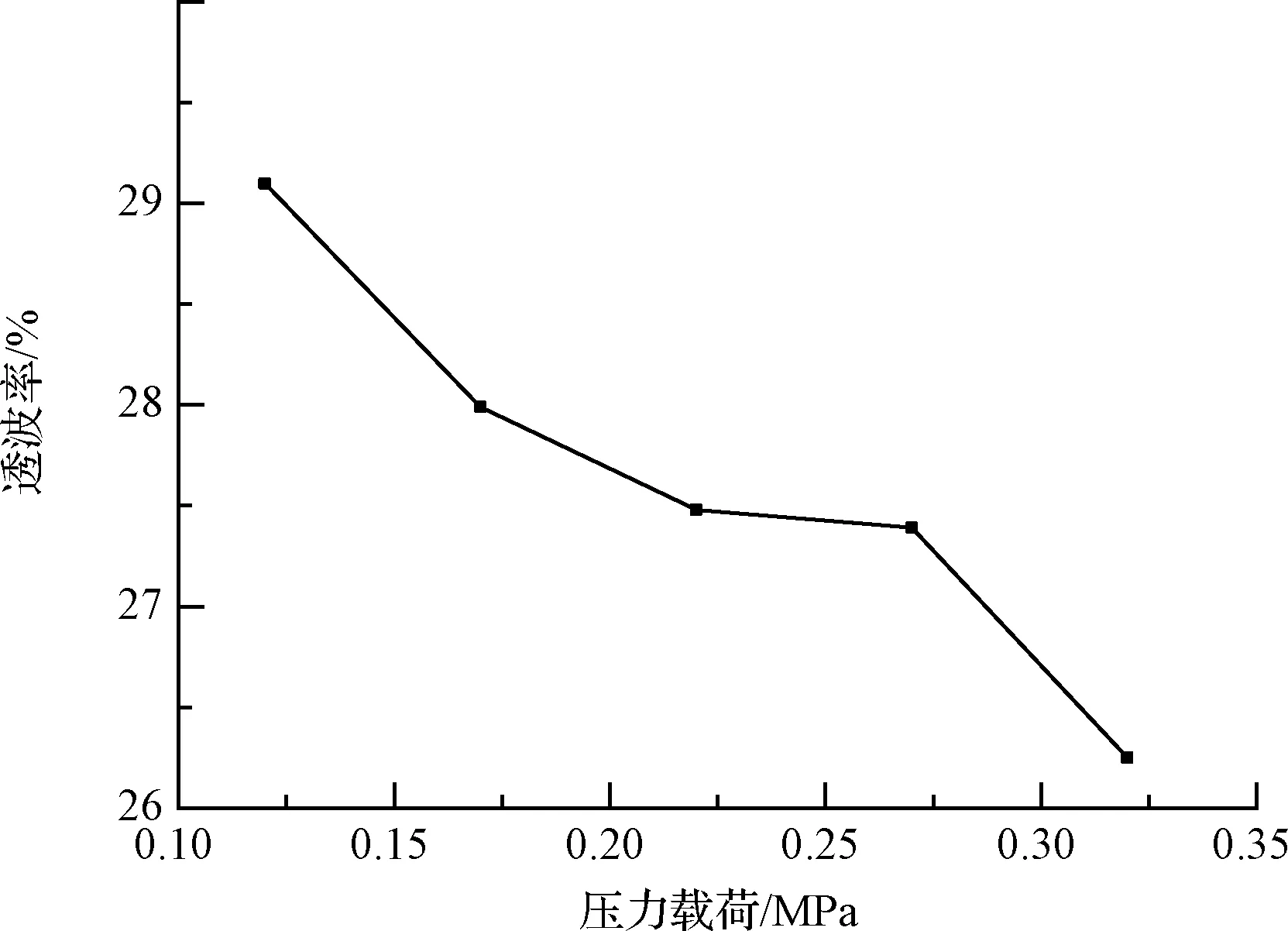
图12 不同力载荷状态下天线罩透波率曲线Fig.12 Transmissivity curve of antenna under different pressure load
由图12可知,天线罩透波率随着气动力载荷的增大而降低。由于主波瓣实际的入射位置位于天线罩前半部分,因此随着天线罩向内凹陷的幅值逐渐增大,直角坐标系下主波瓣的实际入射角θ也在逐渐增大,根据斯涅耳定理,折射角θr也随着天线罩向内凹陷的幅值逐渐增大而增大。电磁波在厚度为d的天线罩中传播通过的距离dr为d/cosθr。当θr逐渐增大时,dr也在逐渐增大。电磁波在天线罩中通过的距离越大,会产生越多的损耗。因此,天线罩的气动力载荷越大,电磁波透过时将会产生越大的电磁损耗,宏观上天线罩的透波性能就越差。综上,在天线罩设计阶段要充分考虑飞行器飞行状态变化所引起的气动力载荷变化对于天线罩透波性能的影响。
4.2 天线罩热-电耦合分析
施加第3.2节的热载荷,可得天线罩的位移和应力云图如图13所示,结构最大变形为1.78 mm,位于距离天线罩最前端;最大应力为80.3 MPa,位于天线罩尾部连接处。
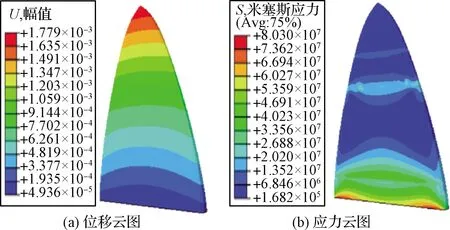
图13 热载荷下天线罩响应结果Fig.13 Response of radome under temperature load
为研究热效应对天线罩电磁性能的作用规律,开展了不同工况下的天线罩热-电耦合分析:仅考虑气动热载荷引起的结构变形对天线罩透波性能的影响(工况b)、仅考虑气动热载荷引起天线罩材料参数变化(相对介电常数和损耗角正切)对天线罩透波性能的影响(工况c)、同时考虑气动热载荷引起天线罩变形和材料参数变化对天线罩透波性能的影响(工况d),并将这些工况下的计算结果与原始常温工况下的天线远场增益(工况a)进行了比对。不同热效应工况下天线远场增益结果如图14所示,不同热效应工况下天线罩的透波性能如表2所示。

图14 热载荷下天线罩透波性能曲线Fig.14 Transmittance curve of radome under temperature load

表2 热载荷下天线罩透波性能Table 2 Transmittance of radome under temperature load
当仅考虑气动热载荷引起的结构变形对天线罩透波性能的影响时,热载荷使得天线罩透波率增强了0.43%,这主要是由于结构变形引起的入射角变化。由图13可知,气动热载荷作用下天线罩底部平板结构位移变化情况为:从天线罩尾部到头部变形均为内凹形式,且幅值逐渐增大,进而造成天线罩的入射角减小。由第4.1节可知,入射角变小会使得电磁波在天线罩中通过的距离减小,则电磁波通过天线罩而引起的电磁损耗越小,从而使得天线罩透波性能增强。但由于天线罩变形幅值较小,其电磁性能增强效果并不明显。
当仅考虑气动热载荷引起天线罩材料参数变化对天线罩透波性能的影响时,宏观表现就是天线罩透波性能的下降。而天线罩的介质损耗角正切随着温度的升高而增加,电磁波通过天线罩时的介质损耗增加,透过天线罩的能量就相对减少,其宏观也表现为天线罩的透波性能下降。
当同时考虑气动热载荷引起天线罩变形和材料参数变化对天线罩透波性能的影响时,热载荷使得天线罩透波率下降了4.18%,这说明材料参数变化对天线罩透波性能的影响占主导地位。因此,选取电磁参数波动较小的电磁材料对于气动热载荷下天线罩电磁性能的提升至关重要。
4.3 天线罩力-热-电一体化分析
开展气动力和气动热共同作用下天线罩的透波性能分析,天线罩的应力和位移云图如图15所示。结构最大变形为3.20 mm,位于距离天线罩最前端672 mm的底部平板上;最大应力为115.1 MPa,位于天线罩尾部连接处。对比材料强度极限可知,天线罩结构满足强度要求。力、热载荷下的天线罩透波性能如图16所示。

图15 力、热载荷下天线罩响应结果Fig.15 Response of radome under temperature and pressure load

图16 力、热载荷下天线罩透波性能曲线Fig.16 Transmittance curve of radome under temperature and pressure load
为研究力、热载荷对天线罩电磁性能的作用规律,开展了不同工况下的天线罩力-热-电一体化分析:仅考虑气动力和气动热载荷引起的变形对天线罩透波性能的影响(工况e)、同时考虑气动力和气动热载荷引起的变形和材料参数变化对天线罩透波性能的影响(工况f),并将这些工况下的计算结果与原始常温工况下的天线远场增益(工况a)进行了比对。不同力、热载荷工况下天线远场增益结果如图16所示,不同力、热载荷工况下天线罩的透波性能如表3所示。

表3 力、热载荷下天线罩透波性能Table 3 Transmittance of radome under temperature and pressure load
当仅考虑气动力和气动热载荷引起的变形对天线罩透波性能的影响时,由于结构变形引起入射角变化,使得天线罩透波性能下降4.32%。由图9、图15可知,天线罩在气动力和气动热载荷作用下的变形形式和气动力载荷作用下变形形式类似。因此,力、热载荷作用下天线罩入射角变大。由第4.1节可知,入射角变大使得电磁波在天线罩中通过的距离增大,则电磁波通过天线罩而引起的电磁损耗增大,从而使得天线罩透波性能下降。
当同时考虑气动力和气动热载荷引起的变形和材料参数变化对天线罩透波性能的影响时,力、热载荷使得天线罩透波性能下降6.12%,这说明天线罩结构变形和材料参数变化对天线罩透波性能均有较大影响。因此,在天线罩的设计阶段,必须充分考虑气动力和气动热载荷对于天线罩透波性能的影响。
5 结束语
本文提出了一种针对天线罩结构的力-热-电一体化分析方法,并探究了气动力载荷、气动热载荷对天线罩透波性的影响规律。以典型天线罩为例,分别开展了力-电、热-电、力-热-电分析。结果表明:
1)气动力载荷引起的结构变形使得天线罩透波性能下降,且透波率随着气动力载荷的增大而减小。
2)在气动热载荷作用下,高温引起的结构变形使得天线罩透波性能增强,高温引起的电磁参数变化使得天线罩透波性能下降,后者对天线罩透波性能的影响占主导地位。
3)在气动力和气动热载荷联合作用下,结构变形和材料参数变化对天线罩透波性能均有较大影响。因此,在天线罩的设计阶段,必须充分考虑气动热和气动力载荷对于天线罩透波性能的影响。

