自适应阵列波束形成算法研究

归达伟

摘要：在世界科技飞速发展的今天，雷达，声纳，无线通信等许多领域有一个非常重要的技术被称为自适应阵列波束形成技术，他也是阵列信号处理的重要部分，经过几十年的研究之后，自适应阵列波束形成技术的理论和相关算法已经有了非常成熟的体系，本文首先介绍了自适应阵列波束形成技术的发展历程，并提出了当前应解决的问题，最后，对自适应阵列波束形成算法进行了比较。

关键词：自适应阵列波束形成技术;问题;算法

引言

波束形成算法，本质上是一种空间滤波的算法，在列阵波束形成技术研究的最初，天线阵列波束形成技术使自适应阵列波束形成技术的基础，自从自适应阵列波束形成技术研究成熟后，被广泛的应用于目标位置，语音识别等领域。它不仅能对来源于四面八方的信号进行准确的识别和处理，将特定方向的有用信号进行处理，形成波束，同时排除了其他方向信号的干扰。但经典的波束信号的阵列响应频率稳定性较差，主瓣宽度和频率的增加呈反比，这样很容易造成信号失真。由于波束形成算法的缺点，我们对自适应阵列波束形成的算法进行了比较，实时调整接近最佳位置的权重集，最终准确识别特定方向的信号，并排除其他方向的干扰。

一、自适应阵列波束形成技術的发展

一九六零年，自适用阵列天线管理系统的研究启动，经过近十多年的发展，自适合阵列波束形成工艺技术已趋于成熟，其基本的理论框架和算法体系已经形成。Goodara等总结和分析了多种自适应阵列波束成形算法。自适应阵列对波束成形过程采用不同的标准来定义自适应权重，并使用不同的自适应算法来实现。主要标准如下。最小均方误差（MSE）标准;Monzingo和Miler在他们的一个图表中表明，4个基准（如最大SN比（SNR）基准、最大似然比（LH）基准和最小噪声色散（NV）基准）在理想条件下是等效的。无论选择了哪个数据，都必须使用特定算法来调整阵列波束模式以实现自适应控制。

有各种各样的自适应算法。而按照计算的具体目标，我们可将它分拆成开环计算和闭环算法。在最初阶段，我们主要专注于闭环算法，包含最小化均方（lms）计算，微分最大分集（dsd）计算，加速梯度（ag）计算及其对它们的变形计算。由于闭环算法没有数据储备，简单可靠。但是，其主要缺陷是收敛到最佳权重的反应持续时间取决于统计特征值分配。在干扰分配的情形下，算法的收敛速率慢，极大影响了应用。所以，在过去的二零年里，人们更关注于开放式循环计算的研究。我们已经提供了一个经典的开环控制系统计算。DMI方法通过直接影响色散矩阵的解胜者hopf方程，获得了最佳权重和取消权重。收敛速率和取消性能都远优于传统闭环算法。由于数字信息的迅速发展，高速智能芯片的问世创造了开环控制计算的良好的先决前提条件。

二、目前自适应阵列波束形成算法存在的问题

计算的持久性和复杂性是自适应算法可行性的关键。传统的自适应波束转换算法没有考虑所采集数据的预期信号元素。在这种情形下，该计算有数据抗性，在此基础上，人们也给出了一些快速收敛算法。但是，尽管在理想情形下（已知预期信号的有限方向向量），因为实际采样数据中含有期望信号信息，因此计算收敛速率明显慢于实际没有期望信号信息的计算速率。尤其是在感知数据不足的情形下，自适应波束算法的实际性能显然不如理论算法。但实际上，影响算法运行质量的最主要原因是实验环境、采样数据、天线板和假设。通常，在可接受的天线板响应和实际天线板响应之间存在误差。自适应天线系统对该误差极为敏感，因为如果发生该误差，在计算表格质量因数时，预期信号被抑制为干扰。在预期信号方向上，不是保持最大利润，而是在预期信号方向上创建零。生殖环境的不规则性、系统元素的局部分散和互连通常导致表对预期信号的响应。

自适应算法修改相关信号的能力实际上是另一个客观问题。在处理平板信息时，往往具有一致的干扰信号，如多维反射和智能干扰。在这些情形下，在传统的自适应方式中，信号被取消。由于虚拟信息源的分配和实际分配不同时，使用了传统的自适应算法，阵列波束的传统自适应格式无法使场适应实际干扰源，波束形成的效率降低。

三、自适应阵列波束形成算法对比

1.最小方差无失真响应波束形成算法

最最低方差系数无畸变反馈波束生成（MVDR）计算的基本原则是将预期的输入信号方向增益限制为1（即，单位增益），从而使阵列的功率最低，即通过控制扰动和噪声，使阵列进功率最低。

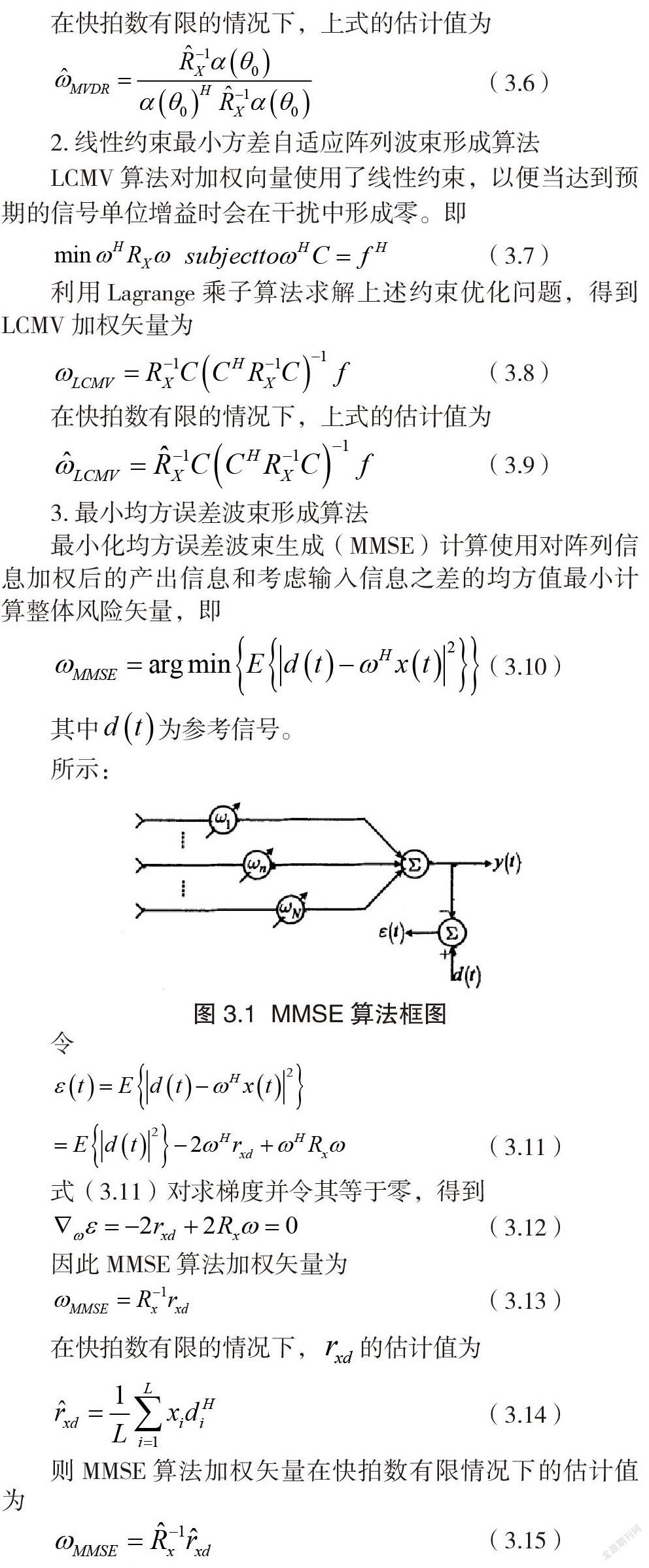
3.最小均方误差波束形成算法

最小化均方误差波束生成（MMSE）计算使用对阵列信息加权后的产出信息和考虑输入信息之差的均方值最小计算整体风险矢量，即

4.广义旁瓣相消器算法

广义旁瓣消除器（GSC）计算，是使用已有的信号方向信息把所接收到的消息更变为二个分支。在经过滤波器、空间拟合（包括所需信息和信息所需方向的干涉）后，上部分支接收参考信息，转换后的期望信息必须符合对无失真响应的要求，而下部支路在经过分块矩阵后，只包含了干扰信号，将上下支路干扰信号的影响用来对经过转换后的信息加以过滤，为干扰信号生成自适应位移，并在不失真的情况下退出所需的上分支信号。GSC结构如图3.2所示：

结语

在本文中，我们介绍了自适应阵列波束成形技术的发展，并提请注意主要问题。目的是为了比较四种自适应算法，即LCMV算法、MVDR算法、，MMS算法和GSC算法。其中，LCMV算法是MVDR算法的发展。LCMV和MVDR算法的基本思想，是在确保信息系统所需要讯号产生的技术基石上减小控制器的输入输出功率范围，以达到自适应扰动和噪音限制。预期的信号。GSC和MVDR算法在数学上是等效的。MMSE算法是最小化初始车牌接收和参考信号之间的差值的均方值。实际上，不需要关于预期信号到达方向的先验信息，但是，应知道参考信号的具体形状。

参考文献：

[1]陈道林. 数据约束下的鲁棒自适应波束形成算法研究[D].电子科技大学，2021.

[2]李菁华. 基于阵列网络的分布式波束形成算法研究[D].电子科技大学，2021.

[3]孙思聪. 基于矩阵重构与导向矢量估计的稳健自适应波束形成算法研究[D].中国科学技术大学，2021.

[4]陈道林. 数据约束下的鲁棒自适应波束形成算法研究[D].电子科技大学，2021.