具有随机黏性阻尼的分数维线性振荡器中的随机多共振

郭筱瑛 周英姿 王利华 王诗心

( 1. 攀枝花学院智能制造学院 攀枝花 617000 2. 西华大学电气与电子信息学院 成都 610039）

0 引言

噪声常被认为对系统输出信号起负作用，因此人们常采用多种措施来抑制噪声以提高对有用信号的输出性能[1-5]；但是，在某些随机系统中，包括电路和生物传感器系统等，噪声可以提升系统对弱信号的检测能力。随机共振就是这样一种当动力系统中存在一定量的噪声时噪声会提高系统性能的非线性现象[6-8]。分数维系统具有对历史状态记忆的优良特性，因此，系统瞬时状态可以包含其在时间上的历史演变过程。分数阶系统在许多领域被广泛研究[9-13]，比如有非黏性的机械过程、记忆效应阻尼效应、摩擦或复合材料响应，以及粘弹性特性模型等。

近年来，分数维系统中的随机共振得到广泛的关注。在这些系统中，阻尼采用具有分数导数的记忆核函数进行数学建模。在分数维导数定义中使用的记忆核函数主要有 Gamma函数、负指数函数和Mittag-Leffer函数三种形式。使用 Gamma函数的分数维导数系统已经得到许多学者的广泛关注[14-24]，用具有 Gamma函数的分数维导数来研究一阶分数维过阻尼线性系统的随机共振机制[14]，分析分数维振荡器输出信号的方差与相关函数[15]，研究周期调制噪声驱动下欠阻尼分数维振荡器中的随机共振现象[16-17]，研究加性分数高斯噪声作用下分数阶振荡器中的随机共振[18]，研究具有随机质量的分数振荡器中的随机共振[19-20]，研究非线性分数阶双稳系统逻辑随机共振[21]，研究色噪声环境下系统记忆性对分数阶布朗马达合作输运特性的影响[22]，研究带反馈的分数阶耦合布朗马达的定向输运[23]等。也有学者将负指数函数作为核函数来分析含时滞反馈与涨落质量的记忆阻尼系统的随机共振[24]，这里的负指数核函数是作者定义的函数。采用Mittag-Leffler函数的记忆核函数可以表示为[25]，其中τ为系统特征记忆时间，α为分数维数。Eα(⋅)为Mittag-Leffler函数[26]，在短时间内表现为拉伸指数，在长时间内表现为逆幂律。当τ→0时，记忆核简化为幂律函数其 中Γ(⋅)就 是Gamma函数。可见，采用Gamma函数的记忆核函数是采用 Mittag-Leffler函数的记忆核函数的一个特例，而后者更具一般性，特别是其中包含系统特征记忆时间τ，可以在复杂无序的非均匀环境中描述介质分子对系统运动产生的记忆效应。因此采用Mittag-Leffler函数的分数维导数可以从特征记忆时间和分数维数两个维度更好地刻画系统的性能。有学者研究了周期外力作用下具有 Mittag-Leffler核函数的通用郎之万方程描述系统中的随机共振[27]，但是对具有 Mittag-Leffler核函数的分数维线性系统中的随机共振研究方面的成果仍然相对较少。

双值噪声由于在数学计算上相对简单，且其极限可产生高斯白噪声和白脉冲噪声，因此在分数维线性振荡器中受到很多关注[14-17,19-20]。另一方面，三值噪声是一种三级 Markov噪声，在不同领域也是常用的噪声模型[28]。对三值噪声而言，扁平参数可以取1到∞的任意值；而对于对称双值噪声，其扁平参数为 1。可见，相对于双值噪声，研究三值噪声对系统的作用更具一般性，研究分数维振荡器中三值噪声的影响具有更广泛的理论意义。文献[18-19]分别研究了受三值噪声扰动的特征频率和质量的分数维振荡器中的随机共振现象，但没有考虑黏性阻尼的因素。黏性阻尼是多谐振荡器动力系统的一个重要参数。Chen L.C.等研究了具有线性黏性阻尼和摩擦系数的 Duffing振荡器的动力行为[29]。有学者研究了具有线性黏性阻尼[30-31]或受双值噪声扰动随机黏性阻尼[16,32]的二阶多谐振荡器中的非线性动力行为。较少文献关注具有Mittag-Leffler记忆核且黏性阻尼受三值噪声扰动的分数维振荡器中的随机共振效应。基于此，本文研究具有Mittag-Leffler记忆核、受三值噪声扰动随机黏性阻尼的分数维线性振荡器中的随机共振现象。

1 数学模型

考虑噪声环境中具有记忆核和随机黏性阻尼的分数维线性振荡器，其数学模型由随机微分方程描述为

式中，λ为噪声的相关率；噪声ξ(t)的扁平率为

根据第二涨落耗散定理[35], 随机力由相互独立的热噪声η0(t)和ηα(t)两部分组成，它们都服从均值为零的高斯分布，自相关函数分别为

当α=1，相关函数式（5）简化为指数形式的标准 Orstein-Uhlenbeck过程[36]。值得指出的是，本文研究的振荡器与参考文献[27]有所不同。这里考虑了随机黏性阻尼，而文献[27]没有涉及。除了加性噪声，还考虑了对黏性阻尼和驱动力的扰动，并假设它们都来源于同一干扰源，而在文献[27]中，仅考虑了加性噪声。另外，本文的模型与文献[17]也不同，后者的扰动为双值噪声，且记忆核为Gamma函数。一般而言，加性噪声来源于系统的外部，故与系统态变量无关。从形式上看，系统（1）的阻尼力包含的随机项ξ(t)为系统态变量与噪声的乘积，即ξ(t)为乘性噪声。由于乘性噪声干扰了系统的结构参数（这里是对阻尼的扰动），导致系统传输函数与噪声参数有关，从而使系统输出信号是噪声参数的线性或非线性函数，因此相对于无噪声的线性系统而言，对系统的求解要复杂一些，有时候可能无法求出其解析解。对于分数维线性系统而言，乘性噪声的引入，在求解过程中会在时域中出现分数导数与噪声乘积的数学形式，表达式很复杂，为了求解方便，需要综合利用微积分、噪声的性质及变换域（这里是Laplace变换）求解方法，将时域中的复杂方程变换为变换域中的线性方程进行求解，最后再利用反变换域方法求出系统输出的时域解析解。

本文采用在分数维线性系统的求解过程中广泛使用的矩方程方法[7,14-20,30-32]，即通过求解系统态变量与噪声ξ(t)乘积的一阶矩满足的方程来求解平均输出幅度。对式（1）两边取随机平均，得

式（1）两边同乘以ξ(t),再进行随机平均，有

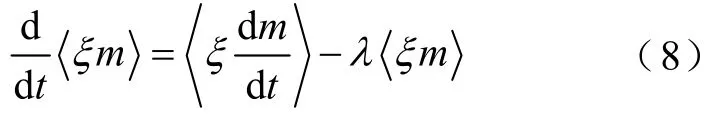
式中，m为ξ(t)的任意函数。令对于关于噪声与系统态变量乘积的新变量x5、x6，利用式（8）进行处理，同时结合式（6）和式（7），可得

利用三值噪声的特性[22]和式（8）、式（10），可得

对这些方程进行反拉普拉斯变换，在极限t→∞下，系统的初始状态的记忆消失，在下面条件下系统有稳态解

稳态条件下系统输出幅度（输出一阶矩x(t)）的幅值可求得为

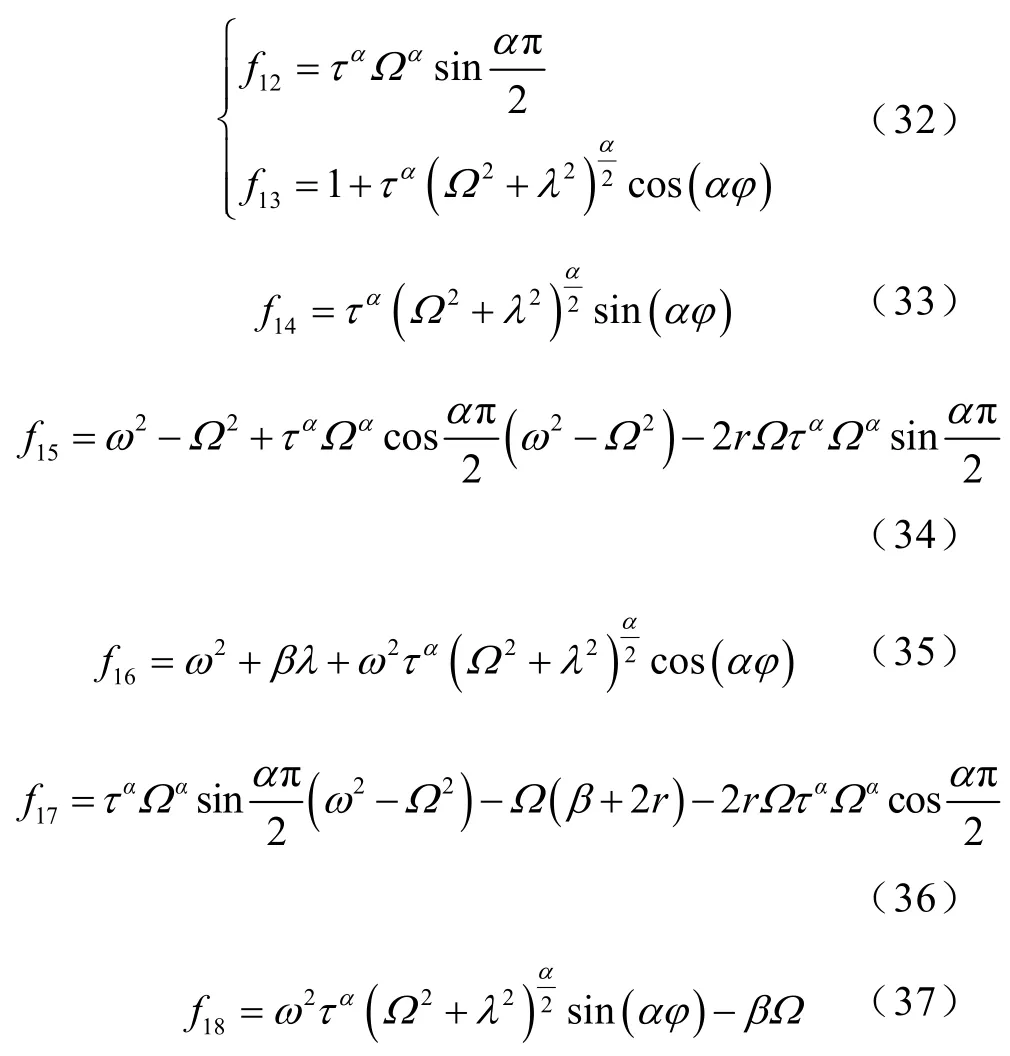
2 随机共振现象分析

利用式（18）～式（37），得到了系统输出幅度SPA的解析表达式。下面分析系统参数和三值噪声参数等对系统输出幅度的非线性依赖关系。噪声扁平参数是三值噪声的一个重要参数，但是对于三值噪声扁平参数对分数维线性振荡器的影响研究相对较少。利用图1～图3来分析噪声扁平参数对系统输出幅度的影响。在图1～图3中，横轴为噪声的稳态概率q（扁平参数g= 1 /(2q)），指三值噪声取值为a或-a这个事件发生的频率，即在考察单位时间内噪声取值为a或-a的次数。稳态概率大意味着单位时间内三值噪声取a或-a这两个值的次数多，而稳态概率小则意味着单位时间内三值噪声取这两个值的次数少。纵轴SPA表示稳态条件下系统输出信号幅度的均值，即系统输出的一阶矩x(t)，它从数理统计的角度来度量系统输出信号的大小，SPA大（小）表示系统输出信号的平均幅度高（低）。图1～图3是系统输出信号幅值随三值噪声稳态概率变化的关系曲线。由图 1～图 3可以看出，在 SPA与稳态概率（扁平参数的倒数，见式（3））的关系曲线上都有一个共振峰，故当其他参数固定时，通过调谐三值噪声的稳态概率，系统输出幅值可实现最大化，意味着单位时间内噪声取值为a或-a的次数/频率为某个值时，系统输出幅值可以最佳。由此注意到，在具有三值噪声扰动阻尼和三值噪声扰动频率的分数维线性系统[18]中，发现了系统输出随三值噪声稳态概率变化而出现一个共振峰的现象，而在三值噪声扰动质量的分数维线性系统[19]中，系统输出幅度随三值噪声稳态概率的变化出现的却是一个最小值，即反共振现象。可见，三值噪声扰动的系统参数不同，系统输出与三值噪声稳态概率的关系曲线也不同。系统输出与三值噪声间的单峰现象在文献[14-20]中没有研究。同时，SPA也是三值噪声的相关率λ、系统频率ω和驱动力的频率Ω的非单调函数。由图1可见，对于较小的概率q(0＜q＜ 0 . 12)，随着λ的增大，SPA单调减小；而对于较大的概率(q＞0.21)，SPA 随着λ的增大而增大。SPA对ω和Ω的非线性依赖性可以由图2和图3按照类似的方法分析。随着λ和Ω的增大，峰值朝q值大的方向移动，如图1和图3所示；而随着ω的增大，SPA的峰值朝q值减小的方向运动，如图2所示。

图1 三值噪声相关率λ取不同值时系统输出幅度SPA与三值噪声稳态概率q的关系曲线，其他参数为r=0.8,a=1 .9,ω=1.2,β=0.3,τ=1,α = 0 .05,Ω=1,A=1Fig.1 The output amplitude SPA versus the stationary probability q of the trichotomous noise for r=0.8,a=1.9,ω=1 .2,β=0.3,τ=1,α = 0.05,Ω=1,A=1 for different values of the correlation rate λ of the trichotomous noise

图2 系统频率ω取不同值时系统输出幅度SPA与三值噪声稳态概率q的关系曲线，其他参数为r=0.8,λ= 0 .2,a=1.9,β=0.3,τ=1,α=0.05,Ω=1,A=1Fig.2 The output amplitude SPA versus the stationary probability q of the trichotomous noise for r=0.8,λ= 0 .2,a=1.9,β=0.3,τ=1,α=0.05,Ω=1,A=1 for different values of the system frequency ω

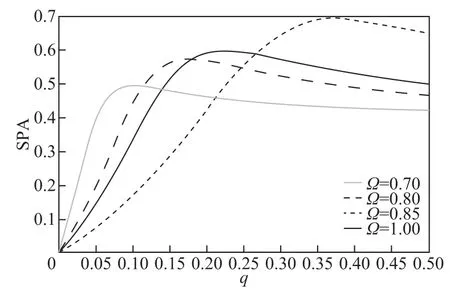
图3 驱动信号频率Ω取不同值时SPA与三值噪声稳态概率q的关系曲线，其他参数为r=0.8,λ=0.2,a=2,ω=0 .9,β=0.3,τ=1,α=0.05,A=1Fig.3 The output amplitude SPA versus the stationary probability q of the trichotomous noise for r=0.8,λ= 0 .2,a=2,ω=0.9,β=0.3,τ=1,α=0.05,A=1 for different values of the frequency Ω of the driving force

需要说明的是，在分析系统输出幅度SPA随着某个参数y变化是否存在随机共振现象时，是基于SPA对y的函数极值这个条件来进行的，即对偏导数 ∂ ( SPA)/∂y= 0 这个等式，看是否存在y值或有几个y值可以使该等式成立。由式（18）～式（37）可见，SPA是系统参数、噪声参数、输入信号参数等多个参数的复杂非线性函数，因此，对于不同的参数y（对于本文而言y指噪声稳态概率q、黏性阻尼r和系统特征记忆时间τ），使 ∂ ( SPA)/∂y= 0 成立的其他参数需要满足的条件可能也不同，因此，在研究 SPA与不同参数曲线上出现共振现象时，同一个参数的取值可能也不同。现在来分析SPA与黏性阻尼r的关系。由图4～图6可以看出，在SPA与r的关系曲线上存在两个极值。随着r的增大，SPA先取一个最小值然后取最大值。而在双值噪声扰动的随机黏性阻尼、具有Gamma函数记忆核函数的分数维线性系统[17]中，在输出幅度随黏性阻尼的变化曲线上存在三个极值。可见，由于对黏性阻尼的扰动噪声不同，系统输出幅度随黏性阻尼变化的非单调行为也不同。另外，本文观察到的与黏性阻尼间的非单调依赖关系与文献[38]研究的具有扰动频率整数阶谐振器中出现的现象类似，而在分数维线性振荡器[14-16,18-19]中没有研究该现象。另外，由图4可见，随着β的增大，SPA的极值由两个变为一个，峰值朝r值减小的方向移动。比较图4与图5、图6发现，随着λ和Ω的增大，SPA的峰值不是朝着一个方向移动，SPA 先移向r值减小方向，后又朝r值增大方向移动；如图4所示，随着β的增大，SPA的峰值仅朝着一个方向移动，即朝着小的r值方向移动。

图4 摩擦系数β取不同值时SPA与黏性阻尼r的关系曲线，其他参数为λ=0.3,a=1,ω=0.6,q=0.2,τ=10,α= 0.9,Ω=1,A=1Fig.4 The output amplitude SPA versus the viscous damping r for λ=0.3,a=1,ω=0.6,q=0.2,τ=10,α=0.9,Ω=1,A= 1 for different values of the friction coefficient β

图5 三值噪声相关率λ取不同值时SPA与黏性阻尼r的关系曲线，其他参数为a=0.5,ω=0.5,q=0.2,β=0.3,τ=1 0,α=0.9,Ω = 1 ,A=1Fig.5 The output amplitude SPA versus the viscous damping r for a=0.5,ω=0.5,q=0.2,β=0.3,τ=10,α= 0 .9,Ω=1,A=1 for different values of the correlation rate λ of the trichotomous noise

图6 驱动力频率Ω取不同值时SPA域黏性阻尼r的关系曲线，其他参数为λ=0.1,a=1,ω=0.5,q=0.2,β=0.3,τ= 1 0,α=0.9,A=1Fig.6. The output amplitude SPA versus the viscous damping r for λ=0.1,a=1,ω=0.5,q=0.2,β=0.3,τ=10,α= 0 .9,A=1 for different values of the frequency Ω of the driving force

记忆功能是分数振荡器的重要特征[12-13]，由于其记忆特性，分数维振荡器可以包含以前状态的动态记忆。在工程系统中，记忆效应和附加特性（例如，非线性）是一种很常见的滞后源[9]。因此，研究分数维振荡器的记忆特性具有重要的意义。图7～图9所示为SPA与系统记忆时间τ的非单调关系。从图7～图9容易看出，在每条SPA曲线上，在较小的和中间的记忆时间τ时都呈现出双峰现象，即出现典型的随机多共振现象。随着τ的增大，SPA增大直到取得第一个最大值，然后单调减小直到一个最小值，接着增大到第二个峰值，最后单调减小。值得指出的是，在文献[27]中，三值噪声扰动的是系统特征频率，而本文中三值噪声作为对系统黏性阻尼的扰动，虽然它们都具有Mittag-Leffler形式的摩擦记忆核函数，但是在文献[27]中，系统输出幅值随记忆时间的变化仅仅出现单峰现象。可见，同样是三值噪声，由于其扰动作用的系统参数不同，系统输出幅度与记忆核的记忆时间变化曲线也不一样。另外，虽然文献[24]也研究了特征记忆时间对系统输出幅度的影响，但没有发现单峰现象，同时，本文发现的系统输出与记忆时间的非单调依赖关系在文献[14-20]中没有研究过。通过分析图7可以发现，SPA也是β的非线性函数。随着β增大SPA两最大值之间的时间差变小；而随着λ的增大，SPA的第一个峰值增加缓慢，第二个峰值减小非常快，两最大值间的差值变长，如图8所示。故对于较小的记忆时间（τ＜0.08），大的噪声相关率λ有利于系统输出性能的提高，而对于较大的记忆时间（τ＞1.2），小的λ能提高系统输出信号。而且，由图9可以看出，驱动信号频率越高（Ω＞1.9），SPA输出幅度越大。因此高的驱动信号频率可以提升分数维振荡器的系统输出性能。

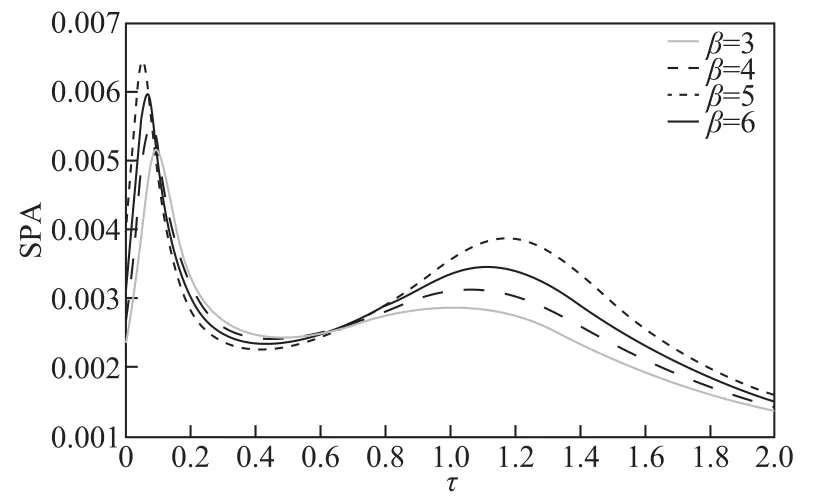
图7 摩擦系数β取不同值时SPA与系统特征记忆时间τ的关系曲线，其他参数为r=0.5,λ=0.1,a=2,ω=10,q=0 .2,α=0.9,Ω=2,A=1Fig.7 The output amplitude SPA versus the characteristic memory time τ of the system for r=0.5,λ=0.1,a=2,ω=1 0,q=0.2,α=0.9,Ω=2,A=1 for different values of the friction coefficient β

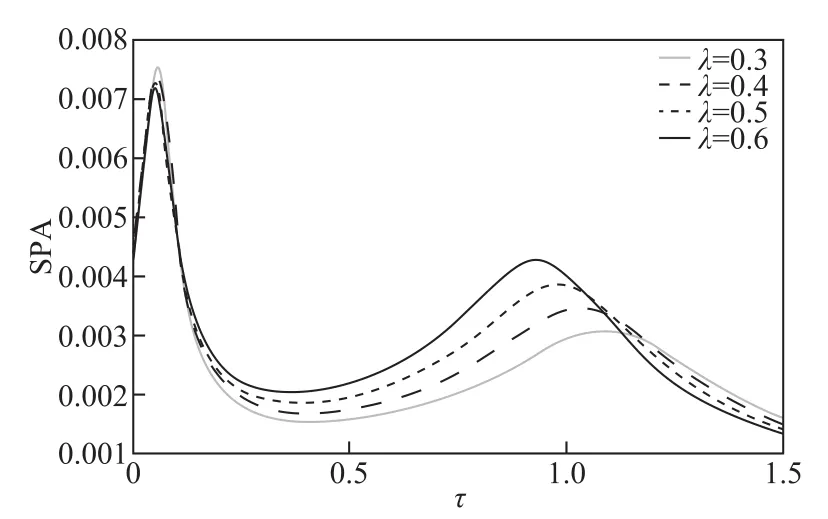
图8 三值噪声相关率λ取不同值时SPA与系统特征记忆时间τ的关系曲线，其他参数为r=0.5,a=2,ω=10,q=0 .2,β=2,α=0.95,Ω=2,A=1Fig.8 The output amplitude SPA versus the characteristic memory time τ of the system for r=0.5,a=2,ω=10,q=0 .2,β=2,α=0.95,Ω=2,A=1 for different values of the correlation rate λ of the trichotomous noise

图9 驱动力频率Ω取不同值时SPA与系统记忆时间τ的关系曲线，其他参数为r=0.5,λ=0.5,a=2,ω=9,q=0 .2,β=5,α=0.9,A=1Fig.9 The output amplitude SPA versus the characteristic memory time τ of the system for r=0.5,λ=0.5,a=2,ω= 9 ,q=0.2,β=5,α=0.9,A=1 for different values of the frequency Ω of the driving force

3 结论

综上所述，本文研究了具有随机黏性阻尼系数和Mittag-Leffler形式核函数、乘性三值噪声作用下分数维线性振荡器中的随机共振现象。分析了噪声扁平率和系统记忆时间对 SPA的影响。利用Shapiro-Loginov公式和Laplace变换，推导出系统稳态输出幅度SPA的表达式。在SPA与噪声稳态概率曲线上，出现一个极值（最大值），在SPA与黏性阻尼和系统记忆时间的关系曲线上，分别呈现两个极值（一个极小、一个极大值）和三个极值（一个极小值，两个极大值），即观察到了随机共振和随机多共振现象。由于三值噪声和分数维振荡器记忆时间在工程中应用广泛，本文取得的结果对于分数维振荡器中的随机共振研究具有普遍和重要的理论价值。