电磁发射弹丸膛口磁场分布特性分析

李湘平 鲁军勇 张 晓 冯军红 蔡喜元

（舰船综合电力技术国防科技重点实验室（海军工程大学） 武汉 430033）

0 引言

电磁轨道发射一体化弹丸的膛内磁场主要取决于放电电流波形和速度趋肤效应，其幅值与电流大小以及弹丸速度有关，而其变化率则主要受电流变化率的影响。弹丸出膛瞬间，膛口电流小于膛内峰值电流，因此膛口磁场幅值小于膛内磁场幅值。受引弧结构的影响，枢轨之间的电流快速转移到引弧器上，虽然流经导轨的总电流未发生大的变化，但此时主电流位置发生了变化，所感应的磁场也发生变化，由于引弧时间极短，导致膛口磁场变化率极大，引弧过程如图1所示。

图1 膛口拉弧过程示意图Fig.1 Schematic diagram of the muzzle arc process

强磁场会带来制导弹丸内部引信安全性、制导控制系统中的磁敏感器件失灵、舵机失效等问题[1]。目前国内外对电磁发射过程中，弹丸内膛的磁场分布特性做了大量研究[2-5]，对制导弹丸内部器件的布局提供了一定的依据。但上述文献均未考虑弹丸出膛后的弹丸内部的磁场分布特性。

针对电磁轨道发射弹丸出膛时出现的特有拉弧现象，本文首先基于柯西（Cassie）电弧模型[6]建立电磁发射弹丸的电流转移模型，获得引弧器上的电流变化；其次将引弧等效为一具有一定长度和半径的导体，构建了由导轨和电枢以及导轨与引弧器两个回路组成的三维瞬态场磁场仿真模型；最后通过引入速度修正项，得到考虑引弧运动的膛口磁场仿真模型。采用该模型，仿真分析了弹丸在出膛瞬间弹丸中轴线上的磁场分布特性，相关结论可为电磁轨道发射制导弹丸内部器件的布局设计提供依据。

1 仿真模型

1.1 电弧转移模型

电磁轨道发射弹丸膛口磁场的剧烈变化主要是枢轨之间电流的快速转移造成的，若要对膛口磁场进行精确建模仿真，则需要建立模型精确刻画引弧过程。有关电弧模型的研究，国内外已进行过大量的研究，包括电弧能量平衡理论和电弧通道的电弧数学模型[7]、将电弧假定为由若干电流元片段组成的链式电弧模型[8]，以及以流体力学和电磁学耦合建模为思想的磁流体动力学 MHD（magnetic hydrokinetics）电弧模型[9]。

MHD模型是目前最接近电弧真实状态的模型，但是仍存在许多缺点，例如，计算比较复杂、耗时过长、不能实现与复杂机械运动的耦合等。链式电弧模型虽然在本质上不是一种场的方法，但其能较好地模拟电弧在灭弧室中被拉长和弯曲的过程，是除 MHD模型外最接近电弧实际形态的数学模型[10]。上述两种模型均能够模拟电弧的膨胀和运动过程，但很难描述电磁发射弹丸出膛瞬间电弧的转移过程，而柯西电弧模型则能很好地实现这一过程[6]。

Cassie电弧模型的方程式[11]为

式中，g为电弧电导；u为电弧电压；τ为电弧时间常数；uc为恒定电弧电压，表示电弧瞬态恢复电压（Transient Recovery Voltage, TRV）方法中的参考电压，取为TRV的峰值。

实际上可将电弧看成一个开关电阻与电枢并联，电枢在膛内时开关呈断开状态，而当电枢脱离导轨后电弧开关开始闭合，则整个电磁发射过程中的电路拓扑如图2所示。图2中，Lr和Rr分别为导轨的电感和电阻，均为随电枢运动位置x变化的值，Ra为电枢电阻，Sarc为电弧开关。

图2 电磁发射等效电路Fig.2 Equivalent circuit of electromagnetic launcher

综上，通过将柯西电弧模型引入电磁发射等效电路中，并根据电枢脱离导轨的时刻控制电弧开关的闭合时刻即可实现电弧转移过程的模拟，进而得到引弧电流。

1.2 膛口引弧瞬态电磁场模型

通过建立包含导轨回路和引弧回路的三维瞬态电磁场仿真模型，并利用电流不突变原理，即转移前导轨电流与转移后引弧电流相等，控制导轨回路和引弧回路之间的开断，模拟枢轨之间电流的转移过程，仿真几何模型如图3所示。

在上述几何模型的基础上，建立瞬态电磁场控制方程，由安培定律可知

图3 仿真几何模型Fig.3 Simulation geometrical model

式中，B为磁感应强度；A为磁矢位；Φ为标量电位；Js为源电流密度；μ和σ分别为导体的磁导率和电导率。根据电流守恒定律，有

式中，V为电动势，假定导轨输入端电流为I(t)，由上述推导可知流过导轨的总电流为

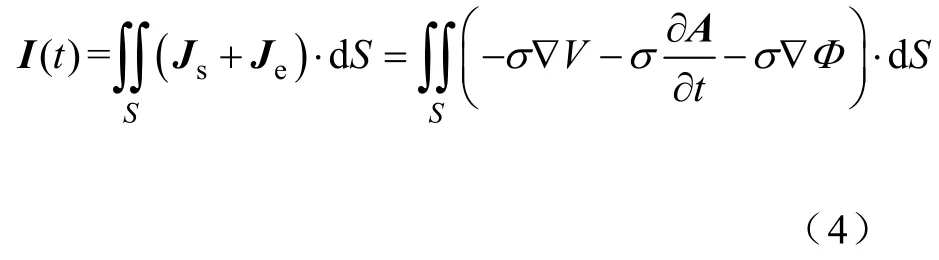
放电总电流用It表示，引弧电流用Ia表示，直接加载在引弧回路输入端。假设弹丸出膛时刻为tm，则加载在导轨回路输入端的电流为

在上述两个回路电流的激励下，通过求解三维瞬态电磁场方程，即可得到电流静态转移时膛口磁场变化。

1.3 引弧运动修正模型

实际上，在惯性力和电磁力的作用下，引弧会产生膨胀并向前运动，相当于一个移动的导体往前运动，其运动速度必将引起膛口磁场的变化。因此，在建模过程中应当考虑引弧运动速度的影响。利用相对运动理论，在模型中以引弧器为参考点，测量点相对引弧器反向运动，并忽略弹丸在横向和上下方向的速度，即只有发射方向的速度，则考虑引弧运动后的测点磁场变化率可表示为

式中，v(t)为引弧速度，并随时间发生变化。

有关引弧运动速度v(t)的计算可通过理论建模分析或试验测量的方式获得。理论建模分析方法包括前面所说的建立链式电弧模型或 MHD模型，建模难度大、计算周期长且不能保证计算精度，本文采用试验测量的方法，利用光学测量技术对电弧弧根运动进行测量[12]，搭建基于三维双目视觉测量原理的电弧弧根运动拍摄和测量系统，如图4所示。通过图像跟踪算法获得弹丸前进方向亮光区域边缘的运动曲线，并将其作为引弧的运动速度。

图4 基于双目视觉的引弧运动测量示意图Fig.4 Arc motion measurement schematic diagram based on binocular vision imaging

在三维摄影测量中，三维双目视觉测量原理如图5所示，如果仅有左相机，由于Oc、M1、M2和m四点是共线的，因此无法通过m点的图像位置唯一确定M1或M2点的三维空间位置，但如果加入右相机，则可以借助右相机中的的图像位置唯一确定出M1或M2点的三维空间位置。

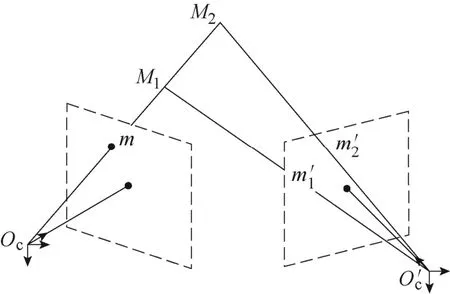
图5 三维双目视觉测量原理Fig.5 Three-dimensional binocular vision measurement principle

使世界坐标系与左相机光心坐标系重合，若已经标定出左右相机参数，则可以计算空间点M1的三维世界坐标为

2 仿真分析

2.1 引弧电流仿真

采用 Matlab/Simulink建立引弧电流转移模型如图6a所示，引弧电流仿真结果如图6c所示，模型中包括脉冲电源放电模块、导轨电感及电阻计算模型、弹丸运动模块以及电弧开关模块。假定弹丸质量m=16kg，弹丸膛内运行距离s=2.36m，电弧时间常数τ=20μs，初始电导率g(0)= 1.0×105S/m，电弧电压uc=2 000V，得到放电总电流It和引弧电流Ia如图6b和图6c所示。

2.2 膛口磁场仿真

2.2.1 膛口引弧运动测量

图6 引弧电流仿真结果Fig.6 Simulation result of arc current

以某次动态发射试验为例，在膛口泄压口位置处架设高速摄像机拍摄引弧过程，考虑到出口弧光光谱复杂，为了得到电弧弧根运动图像，需要滤除除弧光以外的可见光。图7为测量的炮口电弧光谱，测量光谱在590.7nm和769nm处有突变，光强最大的波长为769nm。由于电弧相比其他光要亮很多，因此可确定电弧弧光波长为769nm。

图7 电弧测量光谱Fig.7 The measured spectrum of arc

在上述电弧光谱测量的基础上增加滤光镜，此处选择769nm的滤光镜，拍摄得到拉弧亮光区域的轮廓如图8所示，随着时间的推移引弧逐渐往前膨胀。通过图像处理方法获得弹丸前进方向亮光区域边缘的运动曲线如图9所示，刚出膛时引弧速度达到2 172m/s，大于弹丸出口速度2 000m/s，表明刚开始起弧时，引弧运动速度大于弹丸速度，这与观察到的弹丸出膛瞬间被电弧包裹住的试验现象吻合，是由于引弧过程中电弧等离子体受到电磁力的作用，导致引弧在弹丸出膛速度的基础上继续往前加速。随后引弧受来流空气阻力的影响，其速度快速下降，在100μs内降到接近0。

图8 高速摄像拍摄引弧成像Fig.8 The arc imaging shoot by high-speed camera

图9 引弧运动速度测量曲线Fig.9 The arc velocity measurement curve

2.2.2 膛口磁场仿真及试验验证

为了说明膛口磁场变化的机理，对比引入速度修正和不引入速度修正时膛口磁场的变化。同时为了验证膛口磁场仿真模型的正确性，将三维B点探头测量得到的炮口磁场值与仿真结果进行对比，如图10所示。

图10表明，在不引入速度修正项时，仿真得到的膛口磁场与实测值量值峰值相当，但波形有所差异。引入速度修正项后，仿真值与试验测量值基本吻合，从而验证了本文模型和方法的正确性。

2.2.3 弹丸内部膛口磁场仿真

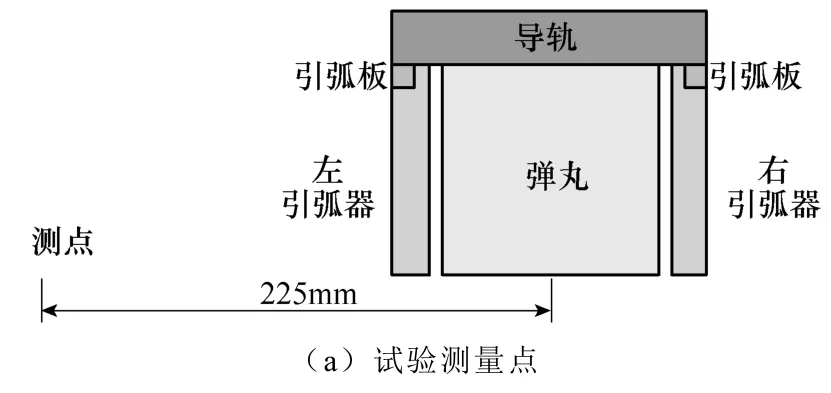
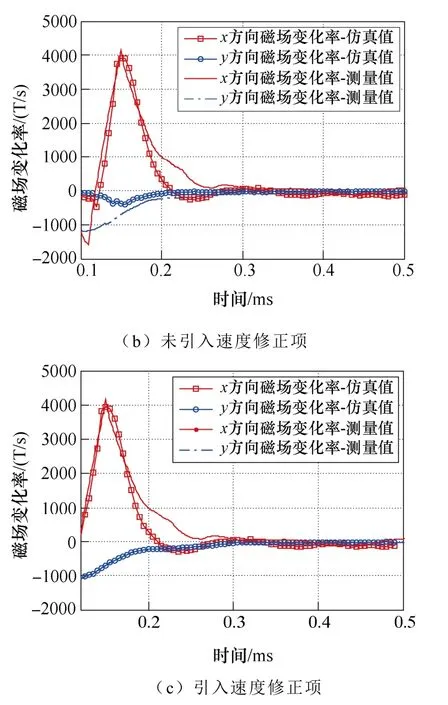
图10 仿真与试验结果对比Fig.10 The contrast of simulation and test results

采用上述模型分析在如图 6b所示放电电流激励下弹丸内部在膛口的磁场分布，选取考察点如图11a所示，得到考察点的磁感应强度和磁场变化率如图11b和图11c所示。需要说明的时，由于考察点随着弹丸一起运动，因此在引入速度修正项时仅修正引弧速度大于弹丸运动速度的时间段，因为一旦引弧速度降到小于弹丸运动速度，考察点离引弧角的位置逐渐增大，速度项的影响可忽略不计，则引入的速度修正公式可表示为

式中，va和vp分别为引弧速度和弹丸出膛后运动速度，并且由于引弧时间较短，可忽略弹丸速度的变化，因此vp可视为常数，其值取为弹丸出膛速度。同时为了对比弹丸膛内与膛口磁场的差异，给出发射过程中考察点磁场在膛内的变化情况，如图12所示。可见发射过程中，弹丸内部磁场强度最大值时刻在膛内，峰值达到0.87T，但最大磁场变化率仅为759T/s，而磁场变化率最大值时刻在膛口，峰值达到8 518T/s，但其磁感应强度峰值只有0.51T。

图11 考察点膛口磁场仿真结果Fig.11 The muzzle magnetic field simulation results of watch point

上述给出了弹丸中轴线上某考察点在膛内和膛口磁感应强度随时间的变化规律，由毕奥-萨伐尔定律可知，在源电流分布一定的情况下，空间某点的磁感应强度与其距离电流元的距离二次方成反比，因此，弹体内部区域所有点的膛内和膛口磁场的对比规律相似。而对于空间分布规律来说，弹丸内部磁场随着离电枢距离的增加均呈现快速衰减的趋势，这与文献[2-3]给出的结论是相似的。理论上，如果考虑弹丸结构和材料，受涡流效应的影响，靠近金属侧的磁感应强度大，致使在弹丸某一截面上的磁感应强度分布呈现出中间小周围大的规律，因此，弹载器件应尽量居中放置，减小磁场对其性能的影响。

图12 考察点膛内磁场仿真结果Fig.12 The in-bore magnetic field simulation results of watch point

由于强磁场对不同弹载器件影响机理不一样，如舵机等带有铁磁材料的器件在强磁场作用下会出现退磁现象，导致舵机性能下降，因此需要对膛内的高幅值磁场进行特定防护。而对于某些电子设备，尤其是带有感性元器件的弹载器件，如弹载电源板，其对磁场变化率更为敏感，过高的磁场变化率会在器件内部形成大电流，从而造成器件的过电流失效，因此需要对膛口的强变化磁场进行特定防护。

3 结论

强磁场环境是制约电磁发射制弹丸研制的重要因素，本文将复杂的引弧过程分解成电流转移和瞬态磁场求解两部分，创新性地引入了膛口磁场速度修正项，从而建立了考虑电弧转移和运动的电磁发射弹丸膛口磁场仿真模型，并对膛口磁场特性进行了仿真分析。分析结果表明，电磁轨道发射弹丸在出膛瞬间受到膛口拉弧的影响，弹上磁场将经历极大的变化，从而对弹载器件的磁场环境适应性提出了更为严酷的考核，与膛内磁场特性不同的是，膛口磁场的磁场强度并不大，但磁场变化率远远大于膛内磁场变化率。本文可为电磁发射制导弹弹载器件的布局设计以及屏蔽设计提供依据。