一种求解等圆Packing问题的柔性位置选择算法

王英聪 张 领 肖人彬

1.郑州轻工业大学电气信息工程学院，郑州，4500022.华中科技大学人工智能与自动化学院，武汉，430074

0 引言

工程中存在着大量的布局(Packing)问题，它们一般要求待布物之间、待布物与容器之间互不干涉，并尽量提高容器利用率[1-2]。作为布局问题的一个典型特例，圆形Packing问题是工业生产中常见的问题，在卫星舱布局[3]、卷材排样[4]、电力电缆设计[5]等领域有着广泛的应用。作为一个经典的NP难问题(non-deterministic polynomial-time hard problem)，很难在确定的多项式内得到圆形Packing问题的最优解,因此，国内外研究者普遍采用启发式方法进行求解，这些方法大致可以分为构造法和优化法两类。

构造法首先对圆形物体排序，然后根据定位规则将圆形物体逐个置入容器中适当的位置，直到所有圆形物体均被放入为止。HUANG等[6]受围棋古谚“金角银边草肚皮”的启发，提出了一种基于最大穴度定位规则的占角算法；LYU等[7]采用PERM (Pruned-Enriched-Rosenbluth method)策略确定放置顺序，采用最大穴度定位规则确定放置位置；黎自强等[8]利用蚁群算法优化放置顺序，利用逆时针外围排列定位规则确定放置位置；AL-MUDAHKA等[9]利用禁忌搜索确定放置顺序，利用分区技术确定放置位置；FEKETE等[10]对容器进行条带化处理，将圆形物体放置到与矩形块四边相切的位置，提出一种结构化条带定位算法；LINTZMAYER等[11]将容器网格化，把圆形物体逐个置入网格并保持相切，提出了有界空间算法和无界空间算法。

与构造法不同，优化法首先将所有圆形物体强行放入容器，然后通过连续优化和格局变换的方式不断地调整圆形物体在容器内的位置，直到所有圆形物体都满足约束条件为止。黄文奇等[12]采用基于交换、跳跃的邻域策略和禁忌策略进行格局变换；何琨等[13]在弹力与拉力模型的基础上，采用基于动作空间的拟物算法优化圆形物体的位置；ZENG等[14]设计了交换和插入两种邻域结构，并结合迭代禁忌搜索进行格局变换；张维等[15]直接利用遗传模拟退火算法优化圆形物体的位置；王英聪等[16]采用基于蚁群劳动分工的空间分配策略进行格局变换；LPEZ等[17]综合考虑了问题的笛卡儿坐标系模型和极坐标系模型，采用非线性规划软件SNOPT优化圆形物体的位置。

上述方法主要针对不等圆Packing问题提出，若将其直接用于等圆Packing问题，求解效果往往不理想。比如，构造法中常用的最大穴度定位规则在等圆问题上有一定的局限性，且对放置顺序的优化是无效的，而优化法中常用的交换邻域策略对等圆问题也无效。近年来，一些学者对等圆Packing问题进行了深入研究。CHEN等[18]将最大贴边度与最大穴度相结合对圆形物体进行定位；黄文奇等[19]利用引力、斥力与弹力的共同作用调整圆形物体的位置；HE等[20]利用拟物拟人策略完成连续优化和格局变换，并结合张弛策略完成跳坑搜索。

本文针对等圆Packing问题提出一种柔性位置选择算法，该算法属于构造法范畴。由于等圆Packing问题中所有圆形物体的半径相同，所以此时构造法不涉及定序过程。由于圆形物体在容器内的可行位置通常不止一个，定位过程的本质就是从多个可行位置中选择一个恰当的位置放置圆形物体，因此，当采用构造法求解等圆Packing问题时，所面临的是一个位置选择问题。在蚁群等社会性昆虫中，个体经常会面临对族群任务的选择，表现为劳动分工[21]。劳动分工的智能性体现在个体无需全局信息和中心控制，仅通过局部相互作用就能选择出符合族群需求的恰当任务。本文借鉴群智能劳动分工的任务选择实现等圆Packing问题的位置选择，提出一种柔性位置选择算法。对国内外55个公开算例的计算结果表明，本文算法是求解等圆Packing问题的一种有效算法。

1 选择视角下的等圆Packing问题分析

1.1 问题描述

等圆Packing问题可描述为[18]：给定一个半径R尽可能小的圆形容器，要求将n个半径为1的单位圆互不干涉地放置在这个圆形容器内。假设圆形容器c0的圆心固定在原点(0,0)，将第i个单位圆ci的圆心坐标记为(xi,yi)，则等圆Packing问题就转化为寻找一种放置(布局)方案X=(x1,y1,x2,y2,…,xn,yn)，使得

(1)

(2)

(3)

i,j=1,2,…,ni≠j

1.2 选择特性分析

构造法在求解Packing问题时将待布物逐个置入容器中恰当的位置。这一过程包含定序和定位两部分，其中定序就是确定待布物的放置顺序，定位就是确定待布物在容器内的放置位置。由于等圆Packing问题中所有圆形物体大小相同，故此时构造法的求解过程特指定位过程。由于圆形物体在容器内的放置位置通常不止一个，因而定位过程可以看成是一个位置选择过程。在构造法的求解框架下，每当新的圆形物体置入容器时就会形成新的格局。下面将结合格局和可行位置的概念，进一步分析等圆Packing问题在定位过程中的选择特性。

定义1格局假设某一时刻圆形容器内已经互不干涉地放置了m(m≥1)个圆形物体，容器外还有n-m个圆形物体等待放置，称这种状态为一个格局Cm。初始格局时，容器内只有一个圆形物体且与容器边缘相切。当所有圆形物体都已放入容器中时，此时的终止格局为合法格局。当容器外的圆形物体无法再放入时，此时的终止格局称为非法格局。

图1 可行位置示意图Fig.1 The sketch of the feasible positions

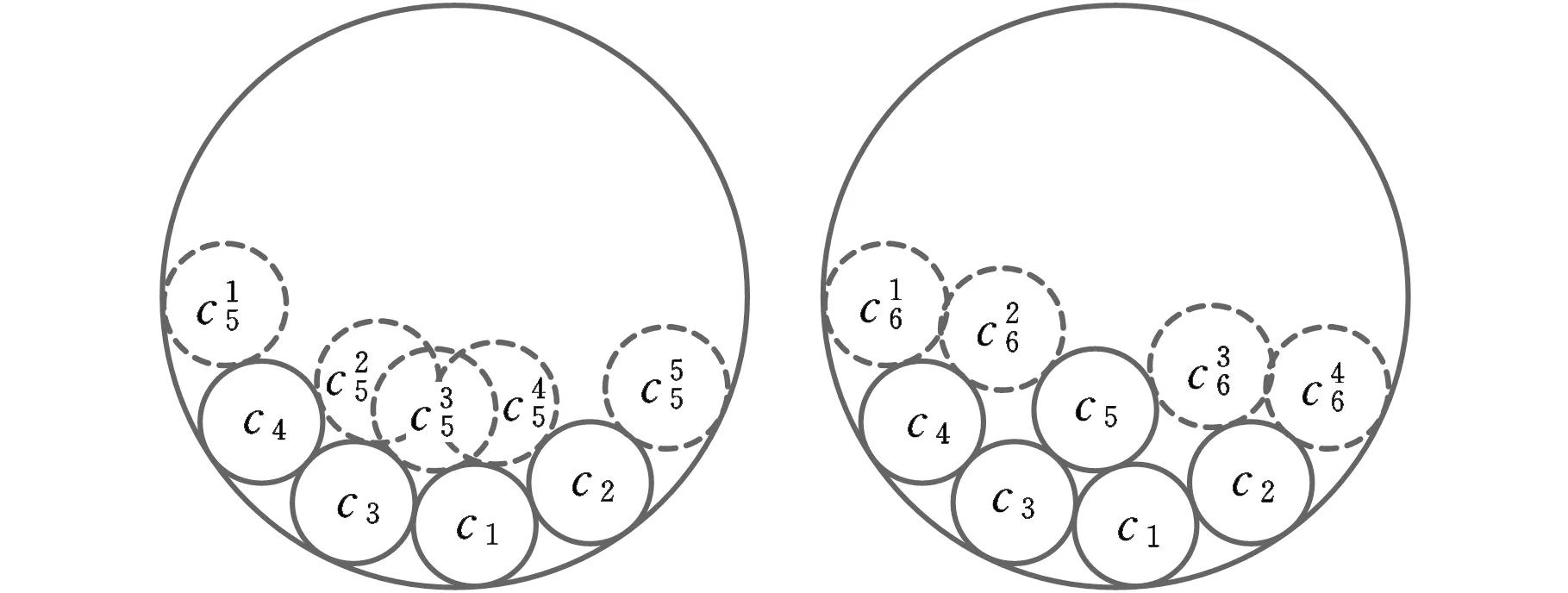
(a)c5的可行位置 (b)选择

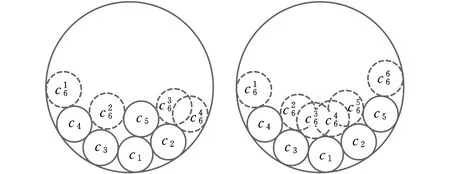
(c)选择选择图2 位置选择特性Fig.2 The position selection characteristics

结合上述分析，等圆Packing问题的位置选择特性可以归纳如下：①在同一格局下，圆形物体在容器内的可行位置通常不止一个；②选择不同的可行位置，将形成不同的格局；③格局的差异体现在已布局空间和未布局空间两个方面；④可行位置对已布局空间的影响体现在紧凑性上，可通过圆形物体在可行位置处与已布局圆形物体之间的距离关系来描述；⑤可行位置对未布局空间的影响体现在完整性上，可通过圆形物体在可行位置处所形成的新可行位置的数量和质量来描述；⑥不同格局下的可行位置之间有重合，也就是说有一部分可行位置是固定的。

2 基于劳动分工的位置选择算法

2.1 相似性分析

在蚁群等社会性昆虫中，族群为了维持生存需要完成各种各样的任务，比如寻找食物、哺育幼虫、维护巢穴、抵御外敌等。劳动分工从宏观上表现为不同的个体执行不同的任务，是个体在局部简单规则作用下涌现产生的一种智能行为[21]。社会性昆虫劳动分工的智能性表现为：在无需全局信息和中心控制的情况下，执行不同任务的个体的比率会随环境自适应调整，而且该比率下的分工恰好满足族群对各项任务的需求。也就是说，在群智能劳动分工的作用下，个体仅通过局部作用就能选择出符合族群需求的恰当任务，因此，群智能劳动分工可以看成是昆虫个体对族群任务的选择。

由1.2节的分析可知，等圆Packing问题在构造法求解框架下可转化成一个位置选择问题。图3描述了位置选择与任务选择之间的相似性。对圆形物体而言，定位过程就是从多个可行位置中选择一个恰当的位置。对昆虫个体而言，劳动分工就是从族群任务中选择一个恰当的任务。如果将圆形物体看成昆虫个体，可行位置看成族群任务，那么利用任务选择就可以实现位置选择。由于构造法是在逐步完善Packing解，在每一阶段的定位过程中只能利用当前格局的局部信息，而当前格局下的最优位置不一定是符合全局的最佳位置，这也是定位过程的难点所在。在群智能劳动分工作用下，昆虫个体仅利用局部信息就能选择出符合全局的恰当任务。群智能劳动分工的这一特点恰好满足构造法对定位过程的要求，这为本文算法的提出提供了理论依据。

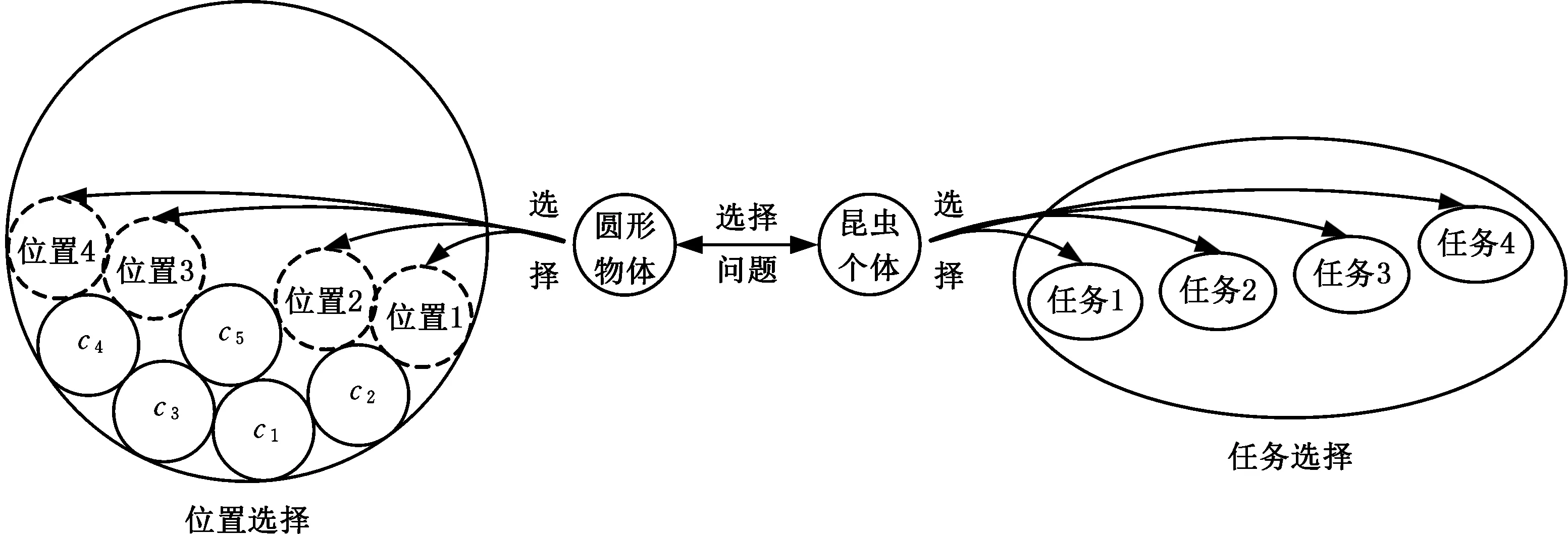
图3 位置选择与任务选择之间的对比Fig.3 The comparison between position selection and task selection

2.2 劳动分工机制

刺激-响应是群智能劳动分工的一种内部机制，可简要描述如下[21]：族群中的每个任务都对应着一个刺激，刺激强度描述了任务的紧急程度；昆虫个体对应每个任务都存在一个阈值，阈值大小反映了昆虫个体执行任务的倾向性；当任务的刺激强度高于昆虫个体的响应阈值时，其选择任务的概率高，反之，选择任务的概率低。BONABEAU等[22]给出了刺激-响应机制的一种量化形式：令S表示任务的刺激，θ表示昆虫个体的阈值，则昆虫个体选择任务的概率P=Sq/(Sq+θq)，其中q为控制响应函数曲线形状的常量，一般取2。THERAULAZ等[23]进一步指出昆虫个体还具有学习(奖励)和遗忘(惩罚)能力：当昆虫个体执行(或成功执行)某项任务时，对应的阈值在学习(奖励)的作用下会减小；当昆虫个体未执行(或未成功执行)某项任务时，对应的阈值在遗忘(惩罚)的作用下会增大。通过刺激和阈值的相互作用，以及阈值的自适应调整，昆虫个体能够灵活地选择族群任务。

2.3 柔性位置选择算法

本节利用群智能劳动分工的任务选择实现等圆Packing问题的位置选择，提出一种柔性位置选择算法(flexible position selection algorithm, FPSA)。根据群智能劳动分工机制，FPSA主要包含刺激和阈值两部分。结合等圆Packing问题的位置选择特性，刺激和阈值的设计可从格局定义下的已布局空间和未布局空间两个方面来考虑。

2.3.1刺激

圆形物体选择不同的位置将形成不同的格局，格局的差异可从未布局空间来描述。未布局空间内可放置的圆形物体越多，说明未布局空间越完整。放置圆形物体时，一般会优先选择使未布局空间更加完整(即潜在位置多)的位置。根据刺激-响应劳动分工机制，刺激越大，个体选择任务的概率越大，因此，可将未布局空间的完整度看作圆形物体选择位置时的刺激。

假设格局Cm下共有u个可行位置，将圆形物体试放到第k个位置上形成新格局Cm+1。若在新格局下有nk个可行位置，且其中有pk对可行位置之间互相重叠，则与第k个位置对应的未布局空间的完整度定义如下：

Ik=nk-0.1pk

(4)

(5)

2.3.2阈值

圆形物体选择不同的位置将形成不同的格局，格局的差异可从已布局空间来描述。已布局空间中圆形物体之间的距离越短，说明已布局空间越紧凑。放置圆形物体时，一般会优先考虑使已布局空间更加紧凑(即彼此距离短)的位置。根据刺激-响应劳动分工机制，阈值越小，个体选择任务的概率越大。由此，可将已布局空间的紧密度看作圆形物体选择位置时的阈值。

假设格局Cm下共有u个可行位置，第k个位置由已布局圆形物体cv和cw(其中一个可能是圆形容器c0)计算得到。将圆形物体试放到第k个位置上，计算它与其他圆形物体cj(排除cv和cw)之间的距离dj，则与第k个位置对应的已布局空间的紧密度定义如下：

Tk=mindjcj∈Cm∪{c0},cj≠cv,cw

(6)

这里对紧密度的计算与文献[6]中的穴度相似。最后，对u个可行位置的紧密度作归一化处理，将圆形物体选择第k个位置时的阈值定义为

(7)

在群智能劳动分工中，阈值还会随着个体成功(失败)执行任务而减小(增大)，使得社会性昆虫的任务选择具有很强的适应性。由可行位置的定义及等圆Packing问题的位置选择特性可知，圆形物体在容器内的可行位置是离散的、固定的。据此，对阈值设计如下自适应调整策略：分别用位置集合Lb和Lw存储最优布局和最差布局中所有圆形物体的放置位置，若第k个位置(xk,yk)出现在最优位置集合Lb中，则减小对应的阈值θk，以提高其选择概率；若第k个位置(xk,yk)出现在最差位置集合Lw中，则增大对应的阈值θk，以降低其选择概率；否则阈值θk保持不变。具体更新公式如下：

(8)

式中，δ、μ分别为奖励和惩罚系数，δ<1，μ>1。

2.3.3选择概率

根据刺激-响应机制，圆形物体选择第k个位置的概率

(9)

最终，圆形物体按照概率大小以轮盘赌的方式确定放置位置。

2.3.4算法流程

综合以上内容，本文柔性位置选择算法的流程图见图4，具体步骤如下：

(1)初始化参数，包括测试算例的圆形物体个数n、容器半径R、阈值奖励系数δ、阈值惩罚系数μ和终止运行时间t。

(2)将容器的圆心置入原点(0,0)，首个圆形物体置入容器底部位置(0,1-R)与容器相切，形成初始格局。

(3)计算当前格局下的可行位置，若可行位置个数为零则转步骤(7)。

(4)根据式(4)和式(6)计算与每个可行位置所对应的未布局空间的完整度和已布局空间的紧密度，根据式(5)和式(7)计算圆形物体选择每个可行位置时的刺激和阈值，根据式(8)自适应调整各个阈值。

(5)根据式(9)计算各可行位置的选择概率，并确定圆形物体的最终放置位置。

(6)更新当前格局，若所有圆形物体都置入容器则成功退出，否则转步骤(3)。

(7)本次迭代结束，将所得布局结果与当前最优布局和最差布局进行比较，更新位置集合Lb和Lw。

(8)判断算法是否达到终止条件，是则失败退出，否则转步骤(2)进行下一次迭代。

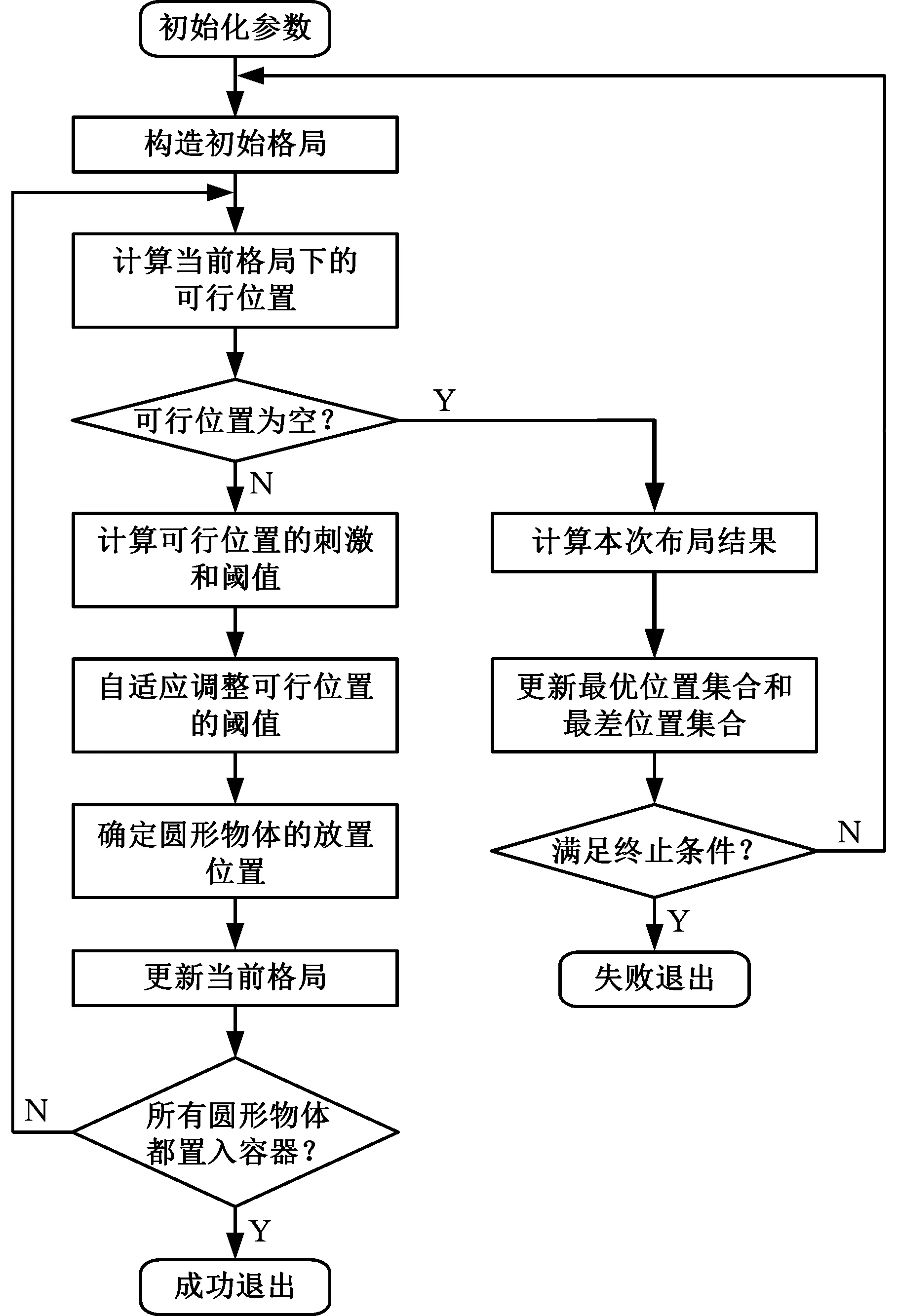
图4 FPSA流程图Fig.4 Flow diagram of FPSA

3 实验与分析

本文采用Java实现FPSA算法，并在主频2.4 GHz、内存4 GB的计算机上进行三组实验。第一组实验旨在设置FPSA算法的参数值，第二组实验的目的是评价FPSA算法的性能，第三组实验则是为了验证刺激-响应选择机制的优越性。本节采用广泛使用的Benchmark算例进行实验[18,20]。

3.1 参数设置

选取Benchmark算例中n分别取值50、60、70、80、90的算例进行实验，容器半径R设置为当前已知最小值，最长计算时间t设置为3600 s。这里主要讨论阈值奖励系数δ和阈值惩罚系数μ的取值对布局效率d的影响(布局效率采用置入容器内所有圆形物体面积之和与容器面积的比值来度量)，从而确定参数的取值。具体方法参照文献[24]中的对比实验取值法，即固定算法中的其他参数，对某一参数随机取值，通过观察平均布局效率确定其较优取值。实验中每个算例独立运行5次。

由阈值的定义可知，δ<1，μ>1。实验发现，随着δ的取值从1开始减小，布局效率大致呈先增大后减小的变化趋势。这是因为：当δ取值较大时，对阈值的奖励程度较小，此时不能有效利用前期搜索所得的一些有价值的位置信息；当δ取值较小时，对阈值的奖励程度较大，此时会过度优先选择前期发现的较好位置，导致搜索容易陷入局部最优。随着μ的取值从1开始增大，布局效率大致呈先增大后减小的变化趋势。这是因为：当μ取值较小时，对阈值的惩罚力度较小，此时会无视一些较差的位置，从而降低搜索效率；当μ取值较大时，对阈值的惩罚力度较大，此时会过度摒弃一些较差的位置；当μ取值恰当时，可以一定程度地接收一些较差的位置，从而增大跳出局部最优解的机会。

考虑篇幅，选取δ和μ的10种组合取值来描述它们对布局效率的影响，从图5中也能基本观察到上述变化趋势。由图5还可以看出，(δ,μ)的取值对布局效率有较大的影响。随着(δ,μ)取值的变化，五个算例的平均布局效率约从72%变化到77%。其中，参数取值为(0.8,1.2)时的布局效率较高。奖励系数δ的意义在于提高迄今为止最优布局中可行位置的选择概率，惩罚系数μ的意义在于降低迄今为止最差布局中可行位置的选择概率。综合来看，当奖励和惩罚的力度较大时，算法搜索的多样性减弱，导致布局结果易于陷入局部最优；当奖励和惩罚的力度较小时，算法搜索不能充分利用之前的有效信息，导致算法的收敛速度降低。

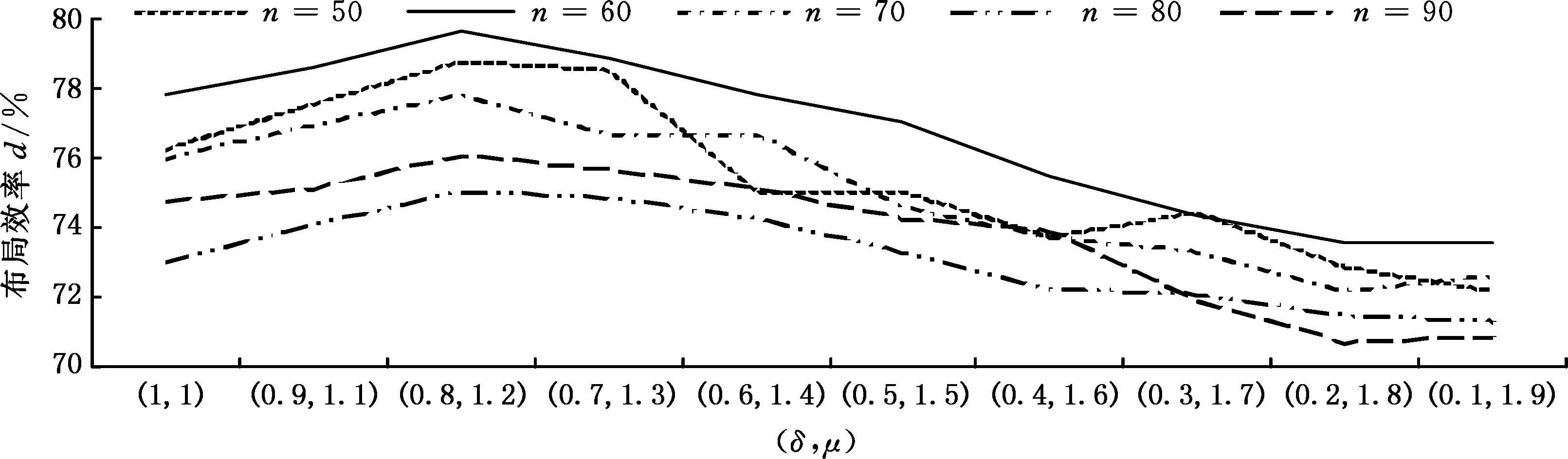
图5 不同(δ,μ)取值下的平均布局效率Fig.5 Average layout efficiencies against different values of(δ,μ)

3.2 计算结果

为了充分测试FPSA的性能，选取目前已知的最新算法贪婪启发式算法(greedy heuristic algorithm,GHA)[18]和拟物拟人算法(quasi-physical quasi-human algorithm,QPQHA)[20]进行对比实验。实验中容器半径R设置为当前已知最小值，最长计算时间t设置为4 h，(δ,μ)设置为(0.8,1.2)。对于每个算例，独立运行FPSA 10次，记录其中的最优布局和对应的平均计算时间。

表1给出了本文FPSA算法与GHA算法的结果比较，二者都属于构造法。FPSA算法采用基于紧密度和完整度的定位规则，GHA算法采用基于穴度和贴边度的定位规则。其中，紧密度与穴度的定义相似，完整度和贴边度都是对未布局空间的一种度量(完整度主要考虑潜在可行位置的个数，贴边度只计算与容器边缘的距离)。由表1可以看出，对于不同n取值的19个测试算例，FPSA算法在5个算例上的计算结果与GHA算法持平，在剩余14个算例上找到了更好的布局。在改进的14个算例上，FPSA算法的布局效率平均提高了0.66%，其中在算例n=100上的布局效率提高最大，为1.86%，在算例n=63上的布局效率提高最小，为0.16%。GHA算法所用机器的CPU主频为3.6 GHz(高于FPSA算法运行环境的CPU频率)，内存为4 GB，用C++语言编程实现。由于算法运行的硬件环境和实现语言不同，故一般不直接比较计算时间，但是由表1可以看出，FPSA算法和GHA算法的计算时间在同一数量级上。与GHA算法相比，FPSA算法在整体上取得了更好的求解效果。

表1 FPSA与GHA的计算结果比较

表2给出了FPSA算法与QPQHA算法的结果比较。QPQHA算法属于优化法，是目前已知的最优算法。QPQHA算法通过拟物策略，将n个圆形物体的布局求解转化为2n维的连续函数优化问题，并采用高效的拟牛顿法进行求解， 布局效果良好。对于这51个测试算例，FPSA算法在49个算例上的计算结果与QPQHA算法持平，在剩余2个算例上找到了更好的布局。QPQHA算法用C++语言编程实现，在8核8 GB的阿里云平台运行。QPQHA算法运行的硬件环境优于FPSA算法，虽然不直接比较计算时间，但与QPQHA算法相比，FPSA算法的计算时间在可接受的范围内。从问题求解的角度来看，FPSA算法充分考虑了等圆Packing问题的特点，QPQHA算法则将等圆Packing问题泛化为数值优化问题。从算法框架来看，FPSA算法和QPQHA算法是两种完全不同的求解模式。FPSA算法在整体上表现出了与QPQHA算法相当的求解效果。图6给出了FPSA算法在算例n=82和n=100上的最优布局。

3.3 分析讨论

FPSA算法设计了完整度和紧密度两个位置评价标准，并通过刺激-响应机制确定圆形物体的放置位置。为了进一步测试刺激-响应选择(stimulus-response-selection, SRS)的优越性，设计如下三种选择方式进行对比实验：随机选择(random-selection, RS)、最小紧密度选择(minimum-tightness-selection, MTS)和最大完整度选择(maximum-integrity-selection, MIS)，其中RS指从可行位置中随机选择放置位置；MTS指选择具有最小紧密度的可行位置，若这样的位置有多个，则从中随机选择一个；MIS指选择具有最大完整度的可行位置，若这样的位置有多个，则从中随机选择一个。

随机选取Benchmark算例中n为54,67,88,95的算例进行对比实验，参数设置与上节相同。对于每个算例，四种选择方式独立运行10次的布局效率分布情况如图7所示(采用MATLAB R2012a绘制)。由图7可以看出，SRS的求解效率最高，MTS与MIS的求解效率次之，RS的求解效率最低。在社会性昆虫中，个体通过刺激-响应机制就能选择出符合族群需求的恰当任务，而且个体的任务选择还会随着环境自适应变化，也就是说，SRS是一种柔性选择方式，能够适应格局/布局环境的变化，在不同算例下都取得了较好的结果。MTS和MIS属于贪婪选择，只选择当前格局下的最优位置，导致搜索容易陷入局部最优。RS无差别地选择放置位置，具有很大的盲目性，导致搜索结果差且不稳定。

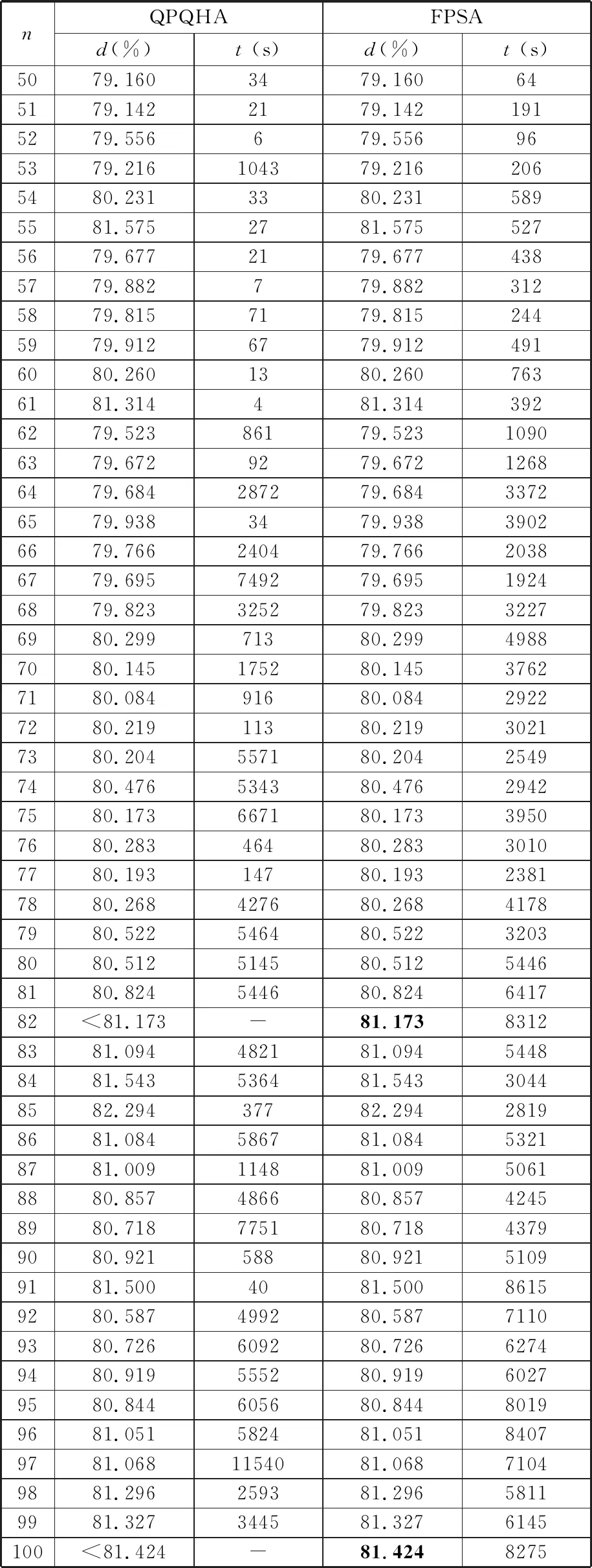
表2 FPSA与QPQHA的计算结果比较

(a)n=82 (b)n=100图6 FPSA最优布局方案Fig.6 The best layouts found by FPSA

(a)n=54

(b)n=67

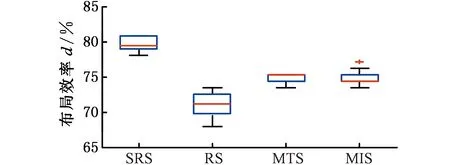
(c)n=88

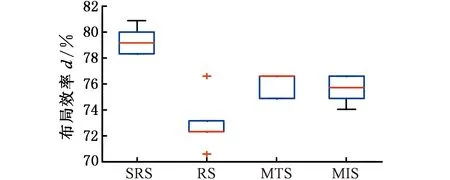
(d)n=95图7 四种选择方式求解不同算例的布局效率分布情况Fig.7 The density of different instances solved by four selection methods

4 结论

针对等圆Packing问题，构造法将圆形物体逐个置入容器，这一过程本质上就是从众多可行位置中确定圆形物体的放置位置。由于圆形物体大小相同，构造过程不涉及圆形物体放置顺序的确定，因此，等圆Packing问题就转化为位置选择问题。借鉴任务选择实现位置选择的思路，本文提出一种柔性位置选择算法(FPSA)。FPSA以刺激-响应的方式实现位置选择，在55个代表性算例上的计算结果表明了FPSA的有效性，同时与随机选择和贪婪选择的对比结果验证了刺激-响应选择方式的优越性。目前已知的群智能劳动分工主要有两种模式：一种是个体与环境交互的劳动分工，其内部机制以刺激-响应为典型代表；一种是个体与个体交互的劳动分工，其内部机制以激发-抑制为典型代表。下一步将研究激发-抑制机制在圆形Packing问题上的应用。