深水桥墩地震动水压力计算方法及建议
王留锋
(郑州市水利建筑勘测设计院,河南 郑州 450000)
1 引言
港珠澳大桥的全线通车标志着中国跨海、跨江大桥的建造技术达到了新的高度。为了减小群桩对水体环境的影响,多数跨海、跨江大桥选择低承台桥墩,即将墩身置于水体中。中国地震频发,深水桥墩在地震激励下会与周围水体产生动力相互作用,即墩身受到地震动水压力的作用。研究结果表明,地震动水压力对桥梁结构的动力特性及地震响应影响显著,不可忽视。因此,如何考虑与计算深水桥墩的地震动水压力显得至关重要。然而,目前地震动水压力计算方法的研究相对较少,且不同方法都存在一定的适用范围,给深水桥墩的设计带来不便。基于此,汇总了目前常用的几种地震动水压力的计算方法,对其进行了简要的分析。
2 深水桥墩地震动水压力计算方法的现状
2.1 Morison方程
1950 年,Morison 方程被提出并用于计算墩柱上的波浪力。该方法假定墩柱的尺寸效应不影响波浪场,且只有当墩柱的横向尺寸D与波浪的波长Lw之比在0.15范围内时,该方程才具有较好的适用性。单位高度墩柱波浪力的表达式如式(1):
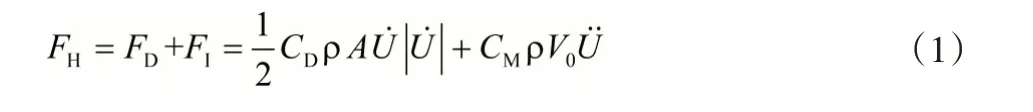
式(1)中:FH、FD、FI分别表示水平波浪力、水平拖曳力和水平惯性力;··U、··U分别表示墩柱某一高度处水质点的水平速度和水平加速度;A 表示单位柱高垂直于波向的投影面积;V0表示单位柱高的排水体积;ρ表示水密度;CD与CM分别表示阻力系数和惯性力系数。
大量研究及实验结果表明,CD与CM不仅与水体中的雷诺数Re和Keulegan-Carpenter数相关,同时墩柱的截面形状对二者的取值也会产生影响。目前,CD与CM的取值主要是通过实验结果或工程经验来选取,对于截面形式为规则的圆形和方形墩柱,常取CD=1.2,CM=2.0。因此,Morison方程本质上属于一种半经验半解析方法。
一般来说,Morison 方程适用于计算静止水体中墩柱的地震动水压力,此时水质点的水平速度和水平加速度即为墩柱在地震作用下的水平速度与水平加速度,通过与结构的动力响应方程进行联立即可求得桥墩地震响应的解析解。袁迎春等研究发现对于深水桩基础桥梁,水平拖曳力对深水桥梁桩柱的地震响应影响很小,可以忽略。基于此,式(1)可以得到进一步简化,新表达式可将地震动水压力视为围绕在墩身周围的水体附加质量,具体表达式见式(2):

式(2)中:Mw为水体附加质量,ρ为水体密度,D、L分别为圆柱体直径和长度。
自20世纪80年代起,国内外研究学者针对Morison方程的精度及适用性开展了大量的实验及理论研究,以期对Morison方程进行修正从而更好地适用于不同工况。此外,李晨曦探究了附加质量法在弹塑性时程分析当中的适用性,结果表明,基于Morison 方程的附加质量法的误差基本在10%,能够满足工程精度要求。
2.2 辐射波浪理论
一般而言,当横向尺寸D与波浪的波长Lw之比>0.20 时,即需要考虑墩柱尺寸产生辐射波浪对原有水体运动状态的影响。辐射波浪理论假设水体为无粘、无旋且不可压缩的理想流体,并将水体中的波浪和结构产生的辐射波浪看作有势运动,进而求得水体中不同区域波动场的速度和液压力。通过对结构同一高度处表面的液压力进行积分即可求得不同高度处由于水体波动而产生的压力。
辐射波浪理论属于解析法,从概念上可知该方法理论上适用于任何截面的墩柱类型,同时对于水体中有无波浪或波流没有明显的限定,且计算精度较高。但该方法的解析表达式较为冗长,广泛地应用于实际工程还存在一些难度。
2.3 数值法
目前,数值法的广义定义即为采用有限元方法建立相应的结构场和流场,并在结构场与流场的交界面设定流固耦合界面进行求解,该方法较为适合复杂截面形式的流固耦合分析,且计算精度较高。目前,有限元求解流固耦合问题的方法包括拉格朗日(Lagrange)法、欧拉(Euler)法以及任意拉格朗日-欧拉(Arbitrary Lagrange-Euler)法,不同求解方法的计算假定有所差异。目前,采用有限单元法建立流固耦合场主要是基于ANSYS 或ADINA 等大型通用有限元分析软件。需要说明的是,目前数值法多采用三维实体单元建立结构场与流场,模型节点自由度较多,计算量较大,计算时间较长,且由于流固耦合界面接触较为复杂,模型整体的收敛性差,对操作者技术水平及硬件条件要求较高。
2.4 改进计算方法
前述地震动水压力的计算方法存在不少限制条件或应用短板,基于此,研究学者提出了一些改进的地震动水压力计算方法。李悦等基于Morison 方程,提出了一种适用于深水大跨径斜拉桥动力时程分析的地震动水压力简便计算方法,拓宽了Morison 方程的适用范围,给Morison 方程向大跨径桥梁结构的应用提供了有利条件。针对辐射波浪理论表达式冗长,难以应用于实际工程的问题,杨万理等基于该理论忽略了自由表面波和附加阻尼的影响,给出了圆形、矩形空心桥墩内外水体动水压力的解析表达式。杨万理等提出了一种混合法,采用辐射波浪法推导圆形桥墩动水压力的简化表达式,乘以数值法计算出的正方形桥墩的形状系数,得到正方形桥墩外水域动水压力,结果表明基于混合法的动水压力表达式简洁,计算效率高,精度好。杨万理等基于Morison 方程、辐射波浪理论等的计算理论基础之上,采用APDL 语言在ANSYS 平台上开发附加质量模块,实现不同截面形式墩柱的附加质量自动计算与添加,通过与传统数值法对比验证了该新型开发模块的适用性。
3 地震动水压力计算方法的建议
Morison 方程由于表达式简单,得到了工程中的广泛应用。但需要注意的是,对于截面尺寸较大的墩柱,Morison方程可能会高估动水压力,且由于Morison 方程中惯性力系数与阻力系数依赖于实验和经验值,即限制了Morison 方程在不规则截面墩柱领域的适用性。因此,对于小尺寸常规截面形式的墩柱,推荐采用Morison方程。
辐射波浪理论由于其严谨的理论推导和清晰的力学概念,理论上适用于各种截面形式的墩柱。但其表达式较为复杂,对于复杂截面墩柱的地震动水压力难以求得解析解。因此,该方法适用于横向尺寸较大的规则墩柱。由于其能够考虑墩柱的尺寸效应,后续研究可以关注基于辐射波浪理论的常用大尺寸截面形式墩柱地震动水压力的简化计算方法。
数值法适用范围较广,对于墩柱截面形式复杂的工况尤为适用。但该方法目前存在计算效率与计算精度相互制约的问题。即模型的计算精度及计算效率受流场大小和网格精度的影响较大,且目前工程界和学术界没有一个统一的建议标准。此外,模型的建模方法较为复杂,流固耦合的接触方式会导致模型收敛困难。这均对操作者的技术水平及硬件水平提出了较高的要求,难以在工程中推广应用。为此,如何使数值法兼具计算精度与计算效率将成为以后的研究重点。
改进计算方法针对目前工程中计算地震动水压力的痛点进行了大量有益的探索,但目前工程中地震动水压力的计算依旧存在计算精度较低、适用范围不明确等一系列问题。因此,后续改进计算方法可重点关注计算精度以及适用范围等问题。
4 结语
①Morison方程表达式简单,方便工程领域推广应用,适用于小尺寸常规截面形式墩柱地震动水压力的计算。②辐射波浪理论力学概念清晰,能够考虑大尺寸墩柱对原有水体运动状态的影响。但因其表达式较为复杂,后续研究可以关注基于该理论的常用大尺寸截面形式墩柱地震动水压力的简化计算方法。③数值法适用范围较广,对于墩柱截面形式复杂的工况尤为适用。但该方法目前存在计算效率与计算精度相互制约的问题。为此,如何使数值法兼具计算精度与计算效率将成为以后的研究重点。

