近海废弃物收集系统压缩装置运动学与动力学分析*
青岛科技大学机电工程学院 青岛 266061
0 引言
近年来,海洋废弃物影响海洋景观,威胁航行安全,对海洋生态系统产生巨大影响。因此,为了更好地保护海洋环境,设计研究出能够回收海洋废弃物的相关装备具有重要意义。一些科研机构及公司着手研究水面漂浮垃圾收集装置[1-4];上海工程技术大学的研究人员提出一种针对水面垃圾清理船的动力推进装置,并对装置进行轨迹分析[5];吉林大学张玉新等设计水面垃圾清理船,对负责清理工作的执行机构进行仿真研究工作,利用ADAMS 确定装置关键参数,并验证结构的合理性[6];陈苏、王中坜等针对水面垃圾清理装置的智能化控制和自动化驾驶等方面进行研究[7,8];上海水产大学工程学院的陈金稳、张丽珍等针对船用明轮的结构进行设计,对明轮的参数做出优化,提高结构效率,提升整机的工作性能[9];Andrew J 设计多种方法相融合的收集装置[10];Choi Gi Eok 研究收集物的粉碎装置,通过机械式结构,实现收集物的高效粉碎[11]。
目前,国内外针对近海废弃物收集系统的装置研究有很多,不同的装置能实现不同的功能,但对收集系统中的压缩装置研究较少[12]。在收集过程中缺乏对废弃物的有效压缩会使收集后的废弃物存在大量水分,且废弃物较为蓬松,无法实现大量的收集,更无法实现收集系统集打捞、运输、脱水、压缩的一体化功能。为此,本文重点研究收集系统的压缩装置,使收集的废弃物能够完成脱水、压缩过程,进而有效增加系统的收集容量,提高收集效率,为后期的运输提供便利。
1 压缩装置的结构组成
如图1 所示,近海废弃物收集系统中压缩装置主要由液压缸、推板、滑轨、压缩舱体、进料斗等部件组成。
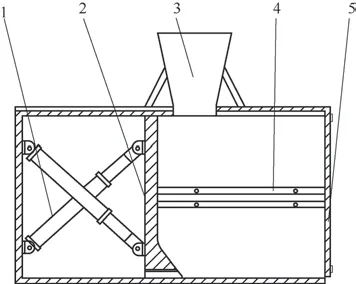
图1 压缩装置结构示意图
2 运动学分析与数值计算
2.1 运动学分析
对压缩装置的执行部分进行运动学分析,研究执行杆件在运动过程中角度的变化与推板位移、速度等参数之间的关系,压缩装置运动简图如图2 所示。
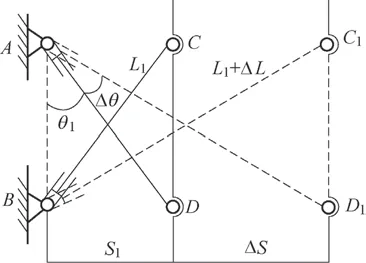
图2 压缩装置运动简图
在图2 中,AD1=BC1,压缩装置在初始工作位置时,液压缸与底座连线夹角为θ1,初始压杆长度为L1,推头与液压缸底座间距为S1。当压缩装置完成压缩后,最终压杆长度为L1+△L,压杆长度伸长量为△L,推头与液压缸底座间距增加△S。在△ABD1中可得

由三角形正弦定理可得
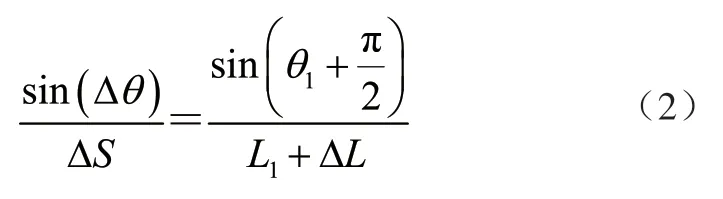
将式(1)、式(2)整合,得到推头的位移△S 与液压缸旋转角△θ 之间的关系为
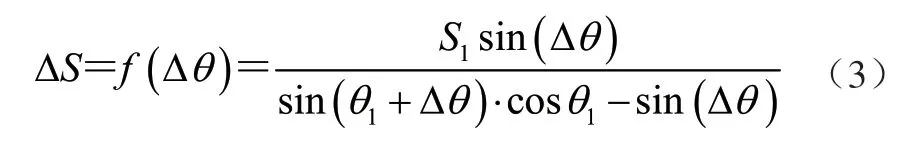
在式(3)中,如果θ1和S1为固定值,△S 与△θ成正比关系。随着液压缸旋转角度的增大,△S 不断增加,当△θ 达到最大值,液压缸的推杆伸长量达到最大,推头到达极限工作位置。
△ADD1三角函数公式对时间取一次导数,可得其推头的移动速度和液压缸的转动速度之间的表达式为
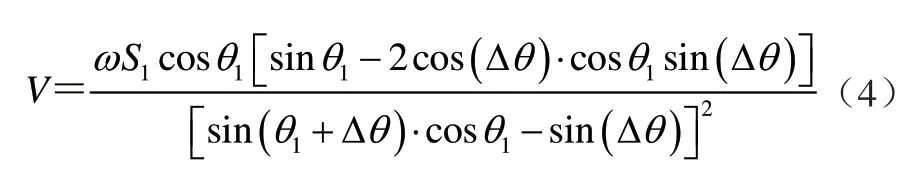
2.2 数值计算
根据压缩装置的运动学分析,使用Matlab 软件分别对推头的位移△S 与液压缸旋转角△θ 之间的函数关系和推头移动速度与液压缸速度之间的函数关系做数值计算。由于设计的压缩推头与液压缸底座间距S1为928 mm,推压液压缸与底座连线的初始夹角θ1为47°,将S1和θ1作为已知量带入关系式,得到推头位移与液压缸旋转角关系曲线如图3 所示;将液压缸速度的变化范围与时间变化范围代入关系式,得到推头移动速度和液压缸速度变化曲线如图4 所示。
由图3 可以看出,随着液压缸旋转角度△θ 的增大,推头的位移△S 也在逐渐变大,变化趋势与预期相符。当旋转角达到最大变化角度,对应的△S 数值为846 mm。由图4 可以看出,在0~3 s 内,液压缸的速度逐渐增大,推板的速度也逐渐增大;当t =3 s 时,推头的移动速度为102 mm/s。
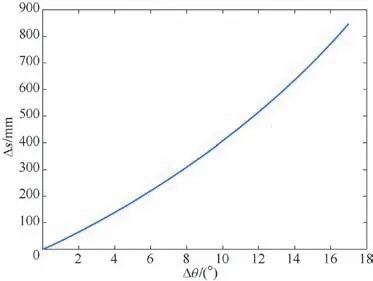
图3 推头位移与液压缸旋转角关系曲线
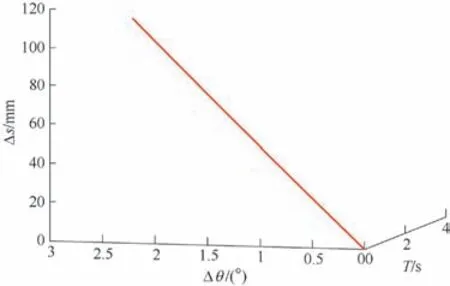
图4 推头移动速度和液压缸速度变化曲线
3 压缩装置的动力学仿真
压缩装置是整个废弃物收集装置的关键机构。在压缩过程中,需要通过推板滑轨实现压缩装置的往复运动,同时液压缸对压缩装置提供动力源。压缩机构设计的合理性关系到整个压缩装置的使用性能和工作效率,因此有必要研究压缩装置在工作过程中的平稳性,保证机构的设计合理可靠。本文对压缩装置做动力学仿真分析,动力学仿真分析流程如图5 所示。
3.1 仿真设置
在动力学仿真过程中,鉴于ADAMS 仿真软件在建模能力的局限性,选择Solidworks 三维软件完成对压缩装置的三维建模。考虑实际工况下的要求,对模型完成混合属性相关参数的设置,在重力设置中选择真实重力存在状态,使虚拟模型更加符合真实情况。在合理的添加约束和运动副、驱动与载荷的同时,简化操作过程,对模型完成动力学仿真分析。

图5 动力学仿真分析流程
1)添加约束和运动副
压缩装置的执行机构缸筒端安装在侧板,侧板与船体固定,无相对运动;执行机构的液压缸杆端安装在推板,与推板间有相对运动。其中,液压缸筒与侧板间所构成的运动副及液压缸杆与推板间构成的运动副定义为转动副。推板和底板间、液压杠杆与液压缸筒间构成的运动副定义为移动副,舱体周围各板定义为固定约束。
2)添加驱动与外部载荷
液压缸的驱动函数选择阶跃函数,压缩推板的外部载荷函数选择Step 函数。阶跃函数的表达式为

式中:x 为自变量,通常为时间的任一函数;x0为自变量的阶跃函数初始值;h0为阶跃函数的初始值;x1为自变量的阶跃函数结束值;h1为阶跃函数的结束值。
3.2 结果与分析
1)推板动力学仿真
推板在X 方向的位移曲线如图6 所示。由图6 可知,推板的初始位置为1 120 mm,第10 s 达到最大位移1 948 mm。在0~10 s 期间,推板从初始位移的1 120 mm 变化到最大位移1 948 mm,△S 数值为828 mm;在第10 s 处液压缸的推杆伸长量达到最大时,推头也到达极限工作位置;在10~13 s 期间,推板进入保压状态,位移保持不变,大小仍为1 948 mm;在13~20 s 期间,液压缸驱动推板返回初始位置。
压缩推板在Y、Z 方向的位移曲线如图7 所示。由图7 可知,推板在工作周期内,其Y、Z 方向位移始终保持不变,装置在Y、Z 方向未发生跑偏,保证了压缩质量。综合推板在X、Y、Z 方向的位移曲线可以看出推板在周期内做直线运动,运动方向沿X 方向,在Y、Z 方向没有大幅度的跳动,总体比较平稳。

图6 推板X 方向位移曲线
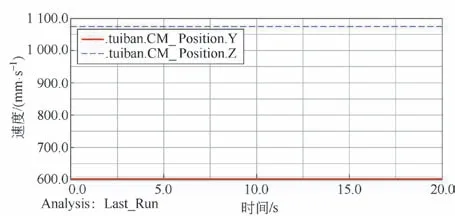
图7 推板Y、Z 方向位移曲线
推板在X 方向和Y 方向的速度曲线如图8 和9 所示。由图8 可知,推板在0~10 s 期间速度先增加后降低,在第4.7 s 达到正向最大速度123.19 mm/s;在10~13 s 期间装置处于保压阶段,速度大小保持不变;在13~20 s 期间速度先增加后降低,在16.8 s 达到最大反向速度176.21 mm/s。
由图9 可知,推板在Y 方向上的最大速度为1.94×10-10mm/s,其数值可以忽略。因此,在工作过程中,推板在纵向比较稳定,波动较小。
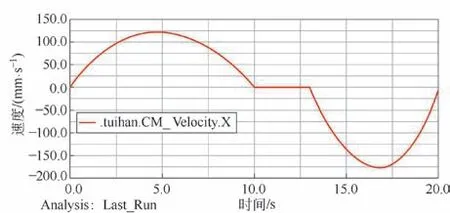
图8 推板X 方向速度曲线

图9 推板Y 方向速度曲线
由于推板在Y 方向速度变化数值很小,故无需分析推板在Y 方向的加速度曲线,推板在X 方向的加速度曲线如图10 所示。由图10 可知,推板的加速度处于缓慢波动,但在第10 s 和第13 s 处的加速度变化较大,对压缩装置会产生较大冲击,影响液压缸的工作寿命。
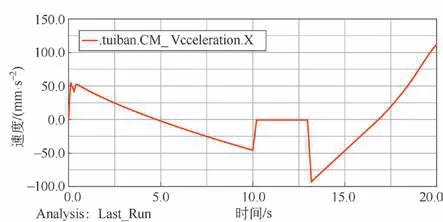
图10 推板在X 方向加速度曲线
2)液压缸动力学仿真
由于压缩装置中的液压缸均为对称分布,故在此仅对中部液压缸的运动参数进行分析,前后液压缸的运动参数与之对应。其中,关于液压缸的转动速度曲线如图11 所示。
由图11 可知,液压缸的速度在0~10 s 期间先增加后降低,在3 s 处达到最大速度,数值为2.78 deg/s;在10~13 s 期间系统处于保压阶段,速度为0;在13~20 s 期间装置处于回程阶段,此时液压缸的速度相对进程数值来说是增大的,在18.1 s 时达到3.94 deg/s,总体来看液压缸的速度变化相对平稳。
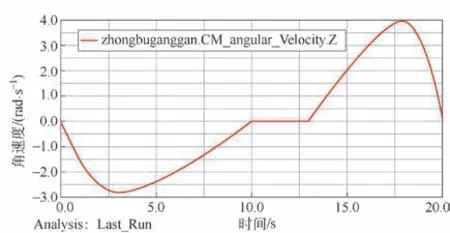
图11 液压缸转动速度曲线
由图11 可知,当3 s 时,在液压缸转动速度为2.78 deg/s ;由图4推头移动速度和液压缸速度变化曲线可知,在3 s 时推头移动速度为102 mm/s;由图8 推板在X 方向的移动速度曲线可知,其在3 s 时速度为108 mm/s,这一结果与Matlab 数值计算结果比较吻合,相对误差为5.9 %。液压缸的加速度曲线如图12 所示。
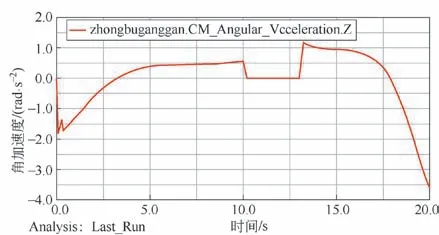
图12 液压缸加速度曲线
由图12 液压缸加速度曲线对比于图11 液压缸转动速度曲线可知,在0~3.2 s 期间,加速度方向与速度方向保持一致,对应速度逐渐增加,增加趋势变缓;在3.3~10 s 期间,加速度始终大于0,逐渐增加,对应速度逐渐降低;在13~17.8 s 期间,加速度平稳降低,对应速度逐渐增加;在17.9~20 s,加速度反向增加,速度逐渐降低。在压缩装置运动的启停点,其加速度发生较大变化,由此可判断在装置的启停和保压启停阶段,装置的稳定性较低。
从液压缸和铰接点的受力情况进行分析,取上部铰接点受力曲线如图13 所示,液压缸受力如图14 所示。
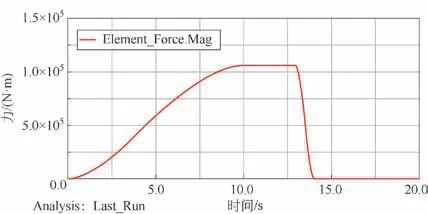
图13 液压缸上铰接点受力曲线
由图13 可知,铰接点处的受力曲线随压缩装置的工作过程先缓慢增加后保持不变,在10.2 s 处达到最大数值为106 460 N。保压完成后,在13 s 处装置开始回程,铰接点处受力急剧降低。
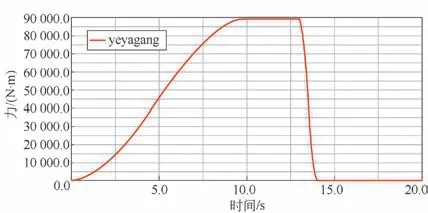
图14 液压缸受力曲线
由图14 可知,液压缸在初始阶段的受力逐渐增加,第10.2 s 处受力达到最大,数值为89 487 N;在10.2~13 s 期间装置处于保压阶段,受力保持不变;在13 s 处装置回程,受力逐渐降低,整体受力平稳,无剧烈增减情况,对装置整体冲击不大。综合图13 和14 可知,液压缸的受力曲线变化与铰接点处的受力曲线变化趋势相同,虽在行程和回程的交界点处存在冲击力,但总体对液压缸的影响不大,仿真数据与实际相符。
液压缸的角度变化曲线如图15 所示。由图15 可知,液压缸的初始角度θ1数值为47°;在行程中,角度逐渐增加,第10 s 达到最大角度63.8°;保压完成后,角度逐渐降低,最终在20 s 时刻点达到初始角度47°。由图15 还可以看出,在△θ 的变化区间内,推板从初始位移的1 120 mm 变化到最大位移1 948 mm,△S 数值为828 mm。这一结果与Matlab 数值计算结果846 mm 比较吻合,相对误差为2.2%。
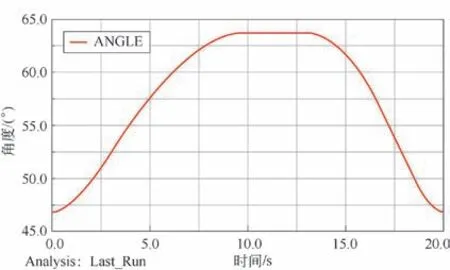
图15 液压缸角度变化曲线
4 结论
1)数值计算结果表明,推头位移随液压缸旋转角度的增大而逐渐增大,推板的移动速度随液压缸速度的增加而逐渐增加,基本保持线性相关。
2)仿真分析结果表明,推板沿X 方向做直线运动,在沿X 方向的运动过程中会对压缩装置产生冲击力,在Y、Z 方向上无大幅度跳动,比较平稳;整个压缩装置在启停、保压启停阶段的稳定性较低,但总体来说装置在启停阶段产生的冲击力对液压缸的影响不大。
3)动力学仿真分析结果与Matlab 数值计算结果比较吻合,推头移动速度的相对误差为5.9%。推头位移的相对误差为2.2%。

