基于LM-BP和SVR的倾倒变形体变形预测
徐卫亚,徐 伟 ,闫 龙 ,陈鸿杰,黄德凡
(1.河海大学岩土工程科学研究所,江苏 南京 210098;2.河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098;3.华能澜沧江水电股份有限公司,云南 昆明 650214;4.中国电建集团昆明勘测设计研究院有限公司,云南 昆明 650214)
边坡及滑坡安全监测资料分析是安全评价的十分重要的环节,得到了国内外学者和工程技术人员的广泛关注和深入研究。由于边坡及滑坡的稳定性与其影响因子之间呈现高度的非线性关系,所以运用人工智能方法挖掘变形监测数据中的时序变化规律,预测未来的变形演化及发展趋势,及时地捕捉各种异常迹象,避免或减少财产损失和人员伤亡具有重要意义[1]。
对边坡及滑坡的变形进行预测,首先需要对已有的监测数据进行处理,如缺失值清洗(插值处理)、非需求数据清洗(删除不需要的数据)、逻辑错误清洗(防止分析结果走偏)和数据归一化处理等,然后将处理后的数据集按照一定的比例划分为训练集、验证集和测试集,基于一定的算法建立预测模型,最后进行预测模型的优化(如使用数据集测试模型、采用优化算法提升训练速度、进行参数调试等)并进行预测,这是进行边坡及滑坡变形预测预报常用的方法[2]。目前水利或土木工程中变形预测预报研究涉及的模型较多,主要包括常规的统计预测模型如回归模型[3]、灰色理论预报模型[4]、生物生长模型[5]、布朗运动模型[6]、卡尔曼滤波法[7]等,以及非线性理论模型如突变理论模型[8]、协同预报模型[9]、支持向量回归模型(support vector regression,SVR)[10-11]、神经网络模型[12]、M5′-主成分模型树[13]等。关于支持向量回归和神经网络模型的研究,Liu等[14]将采用支持向量回归预测的趋势序列与采用长短期记忆神经网络预测敏感性状态相融合,建立了滑坡位移预测的非线性模型,对白水河滑坡进行位移预测研究;黄健等[15]将灰色模型、改进的自适应遗传算法和小波神经网络结合建立预测模型,对垮梁子滑坡进行位移预测研究;李麟玮等[16-17]建立Bootstrap-KELM-BPNN模型,结合灰狼优化算法、最大信息系数和支持向量回归建立预测模型,对滑坡进行变形预测研究;杨帆等[18]结合人工蜂群算法和支持向量回归建立预测模型,对滑坡进行变形预测研究;Yang等[19]提出了一种基于时间序列分析和长短期记忆神经网络的滑坡位移预测动态模型,对滑坡进行变形预测研究。Du等[20]基于时间序列和反向传播神经网络模型,对滑坡进行变形预测研究。但基于神经网络模型和支持向量回归模型进行倾倒变形体特别是库坝区倾倒松弛岩体边坡的变形建模与预测的文献尚不多见。
本文基于澜沧江黄登水电站1号倾倒变形体表面位移实际监测资料,以时间、库水位、降雨量、温度作为输入参数,以位移变形作为输出参数,构建LM-BP(levenberg marquardt back propagation,LM-BP)神经网络模型和SVR模型,对倾倒变形体进行变形预测。通过模型优化将预测结果与实际监测数据的比较,验证预测模型的可靠性和适用性。
1 LM-BP神经网络模型
BP神经网络算法主要思想是通过隐含层将输出误差依次反向传播给输入层,各层的节点分摊误差得到误差信号,各节点根据误差信号修正权值[21]。传统的BP神经网络算法存在学习新样本而遗忘旧样本的趋势、收敛慢、对初始权值的选取敏感、容易陷入某个局部极值点以及泛化能力弱等问题。针对这些问题,学者们提出了改进算法,如附加动量项、自适应学习率算法、Levenberg-Marquardt算法(LM算法)等。LM算法[22],由经典的Newton法发展而来,运用Guss-Newton法在最优值附近生成一个理想的搜索方向,可以保持较快的下降速度,在Guss-Newton法和最速下降法之间自行调整权值,使误差的搜索方向沿着恶化方向进行,提高网格的泛化能力和收敛速度。LM-BP算法的训练流程如图1所示,各个步骤主要完成内容:(a)初始化。随机产生权向量,确定所有样本误差平方和达到收敛标准;(b)求样本输出误差。主要计算隐层节点的输出、输出层节点的输出以及输出层节点的输出误差;(c)求Jacobian矩阵;(d)求权向量的调整量。
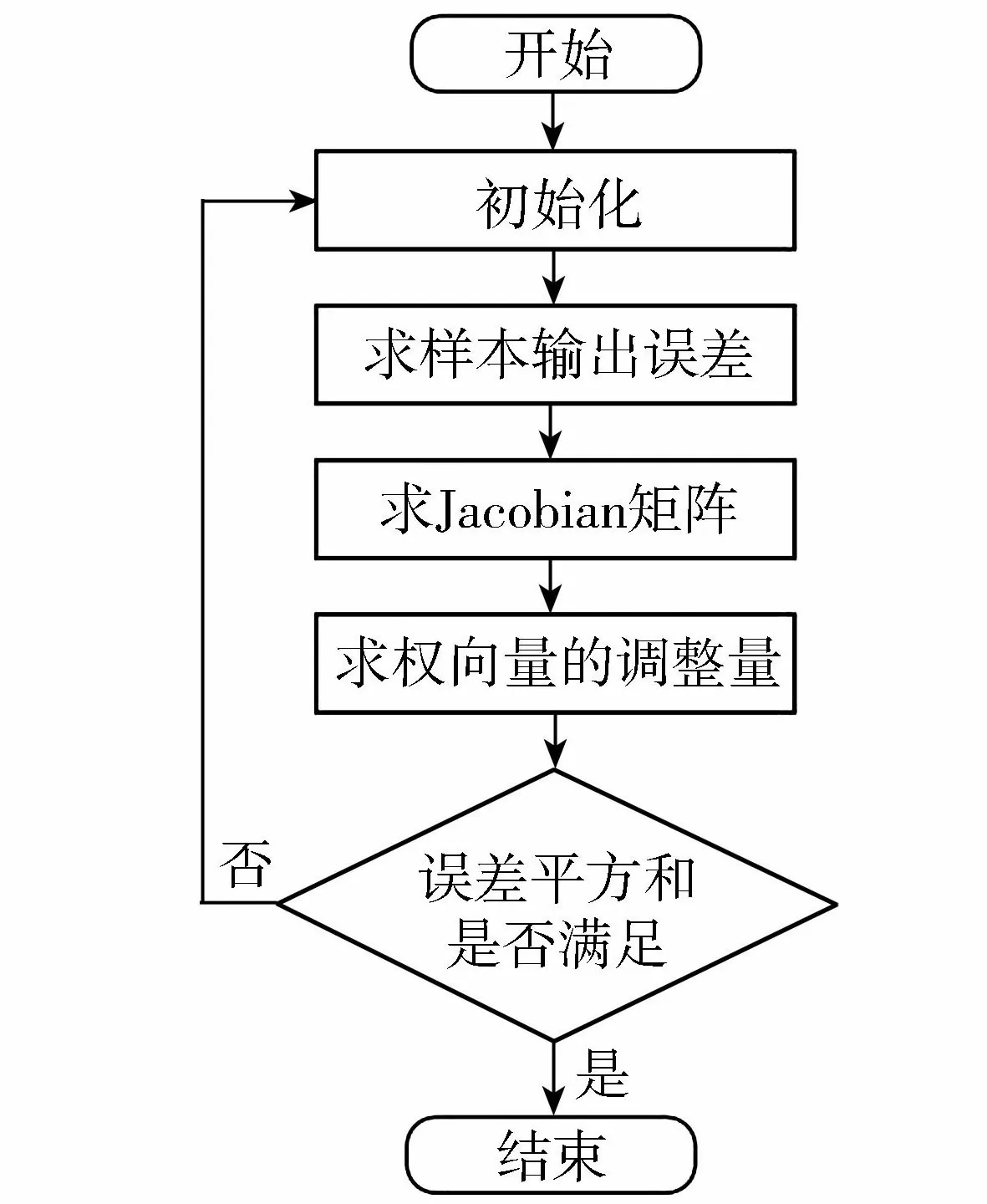
图1 LM-BP训练流程Fig.1 Flow chart of LM-BP training
2 SVR 模 型
SVR模型由Vapnik[23]提出,被广泛应用于求解非线性问题。SVR模型通常将样本数据分为训练样本和测试样本,然后将预先选择的训练样本映射到高维度特征空间对这部分数据进行计算,在最优决策函数模型的空间中获得最佳拟合效果,测试样本用于验证、分析模型效果。SVR训练流程如图2所示。
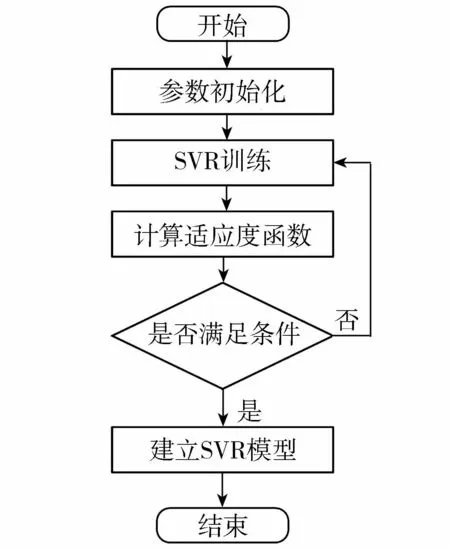
图2 SVR训练流程Fig.2 Flow chart of SVR training
SVR模型解决的是一个凸二次规划问题,得到的是全局最优解,克服了在BP神经网络中难以避免的局部极值问题;将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性决策函数实现原空间中的非线性决策函数,巧妙地解决了维数问题,并保证了较好的推广能力,而且算法复杂度与样本维数无关。该模型具有简单的结构,少量的样本数量即可实现模型学习,且表现优于传统BP神经网络。
3 黄登水电站1号倾倒体变形分析
3.1 1号倾倒变形体概况
1号倾倒体发育于澜沧江黄登水电站坝址区上游右岸1号沟侧近坝库岸约700 m处,主体垂向分布范围1 480~1 830 m高程(局部1 650~1 910 m),宽度约400~500 m,水平发育深度约28~200 m,厚度为30~104 m,总体积约700×104~800×104m3,岩体卸荷强烈,松动变形明显。该倾倒变形体在水库水位变化或降雨等水动力作用影响下,变形破坏机理及安全性评价需要进一步深入分析。1号倾倒松弛岩体发育范围内共布置有9个外观变形测点,其范围和监测点布置如图3所示。

图3 1号倾倒变形体及监测布置Fig.3 No.1 toppling deformed slope and monitoring arrangement
3.2 1号倾倒体变形特征及影响因素分析
图4为1号倾倒变形体的典型剖面。1号倾倒变形体分布区段河谷总体方向为NNE向,岸坡延伸方向与地层走向近于平行,岩层陡倾坡内,属典型的纵向谷逆向坡,具备岩体侧向倾倒变形的地形临空条件。在1号倾倒松弛岩体发育范围附近,斜坡岩体下部主要由似层状浅变质火山碎屑岩及片理化变质凝灰岩条带构成。地层及片理走向与坡面近于平行,倾向坡内、总体倾角约∠75°,上硬下软。1号倾倒松弛岩体的倾倒变形破裂现象较为复杂,其主要受顺向河谷地形、陡倾坡内的似层状及板片状岩体结构两方面因素控制。岩体内部的“倾倒蠕变”、岩体底界的“倾倒-滑移”变形和岩体后缘深部“倾倒-弯折”变形。倾倒变形体的弯曲倾倒破坏机制可归纳为重力引起弯曲折断与水动力作用触发失稳。
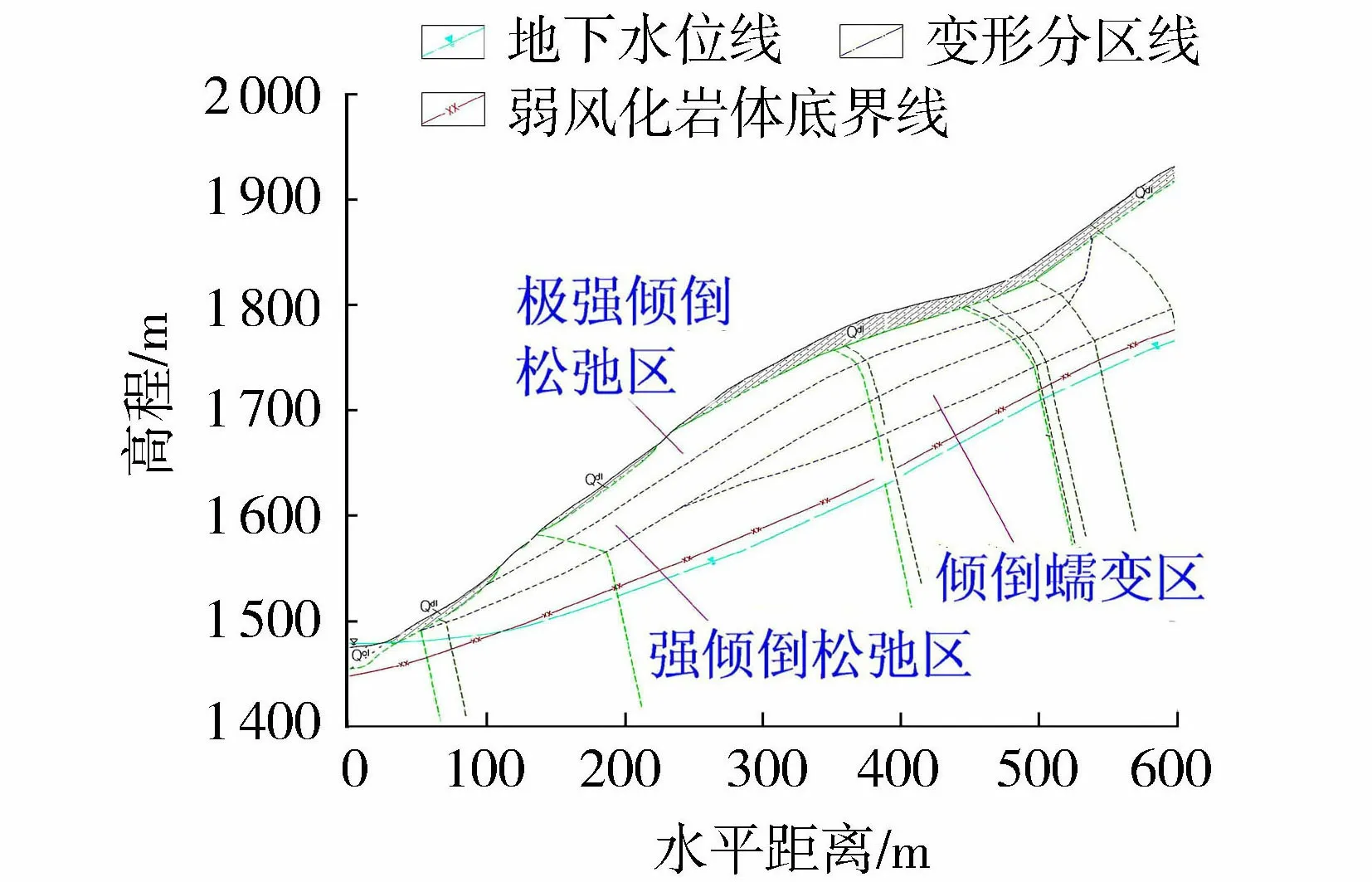
图4 1号倾倒变形体典型剖面Fig.4 Typical profile of No.1 toppling deformed slope
水动力作用是1号倾倒体在黄登水电站运行期变形破坏的主要控制因素。图5为1号倾倒体外观变形测点GTP06的累积位移、累积位移变化和降雨量、库水位、温度关系图。每年7—9月为当地的雨季,降雨时间集中且降雨量明显增大,相应的累积位移、累积位移变化速率增大,降雨对倾倒体变形的影响具有一定的滞后性。一方面,降雨形成地表径流冲刷1号倾倒体表面松散的岩土体;另一方面,随着降雨时间的增加,雨水沿着倾倒体的裂隙下渗,弱化滑带上的岩土体、增加倾倒体的重度,从而增大下滑力、减小抗滑力,不利于倾倒体的稳定。
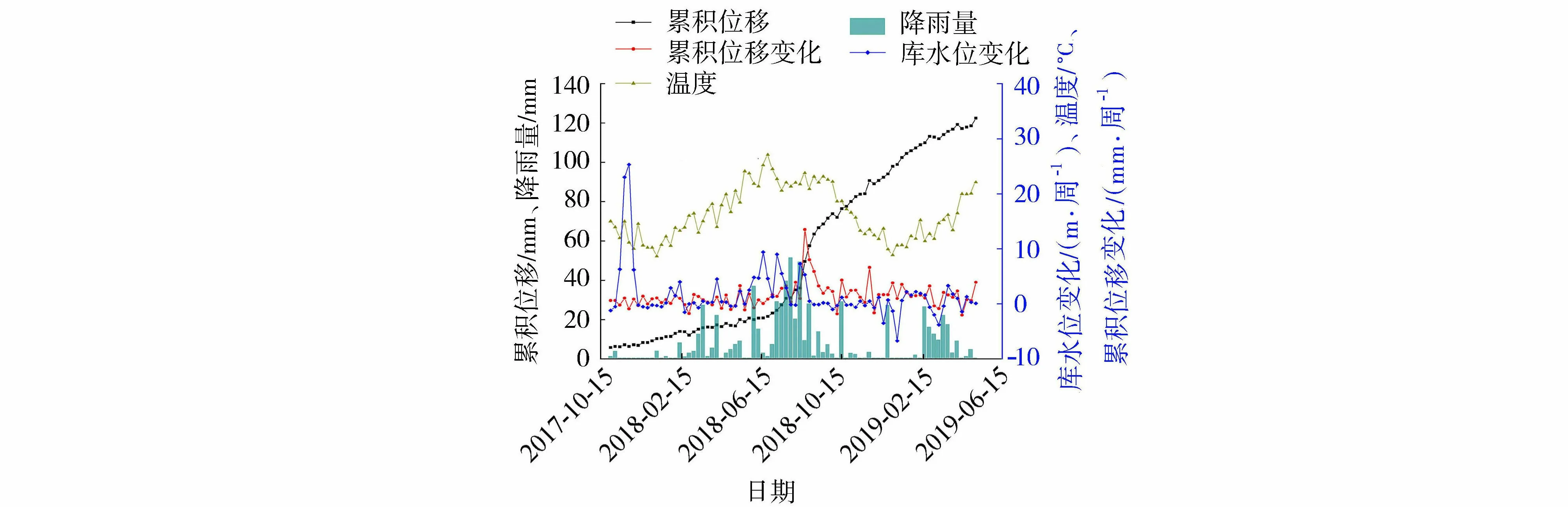
图5 1号倾倒变形体表面位移、位移变化和降雨量、库水位、温度关系Fig.5 Relationship between deformation (surface displacement and displacement change) and influencing factors (rainfall,water level and temperature) in No.1 toppling deformed slope
黄登水电站于2017年11月中下旬开始第一阶段蓄水,库水位上升,1号倾倒体的累积位移、累积位移变化速率持续增大。2018年5月下旬开始第二阶段蓄水,2018年8月下旬库水位升至正常蓄水水位,期间库水位变化持续增加,同时1号倾倒体的累积位移、累积位移变化速率迅速增大,库水位变化峰值滞后于1号倾倒体累积位移变化速率峰值,库水位变化对1号倾倒体变形的影响具有一定的延迟效应。2018年9月后,库水位下降影响倾倒体的变形。温度的变化会影响水的黏滞性,进而影响库水和降雨入渗,而库水位变化和降雨对坡体变形影响是显著的,因此温度间接影响着坡体变形。
考虑到1号倾倒变形体受到水动力作用的显著影响[24],结合以上分析本文以库水位、降水量、温度和时间作为输入参数,以1号倾倒变形体的变形作为输出参数,构建LM-BP神经网络模型和SVR模型对1号倾倒变形体的变形进行预测分析。
3.3 1号倾倒体变形预测分析
首先对已有的实际监测数据进行数据清洗等处理,然后将处理后的数据集建立LM-BP神经网络模型和SVR模型。LM-BP神经网络模型通过均方误差MSE(mean squared error)、拟合优度R2和误差的大小反映拟合效果以及对该边坡变形预测的可靠性。SVR模型通过惩罚系数C、核函数参数g、R2、MSE和误差的大小反映拟合效果以及对该边坡变形预测的可靠性,并运用2个模型预测监测点GTP06的累计变形。由图6可知,在正常工况下,1号倾倒体外观变形测点GTP06累积位移的实测值与LM-BP神经网络、SVR的预测值相差不大,累积位移的变化趋势基本一致且累积位移值将继续增长,预计从监测的第995 d至第1 359 d,LM-BP神经网络模型预测的累积位移从152.43 mm增长至173.93 mm,SVR模型预测的累积位移从150.32 mm增长至169.40 mm,期间位移2种预测方法的位移增长趋势大致相同

图6 监测点GTP06累积位移预测曲线Fig.6 Prediction curve of cumulative displacement for monitoring point GTP06
在正常水位调度、降雨情况下,LM-BP神经网络模型的R2=0.99、MSE=1.94、最大误差为2.53%、绝对误差最大值为3.79 mm,SVR模型的C=6.70、g=0.09、R2=0.97、MSE=2.67、最大误差为4.35%、绝对误差最大值为5.76 mm,可见LM-BP神经网络模型和SVR模型的精度都比较高,且LM-BP神经网络模型的精度比SVR模型的精度高。由图7~8可知,LM-BP神经网络、SVR方法预报分析的位移变化速率和位移变化的加速度曲线仍在变化,倾倒变形体的变形仍然在变化,应予以关注,并加强监测预警、水位调度管理,进一步加强水库水位调度方案与倾倒变形体安全保障之间的系统研究,深化监测预警系统研究。库水位变化、降雨等因素是影响1号倾倒变形体变形的重要因素,合理的水位调度可以一定程度上控制该倾倒变形体的变形。LM-BP神经网络和SVR模型考虑了水动力作用,2种方法的变形预测研究结果可为该倾倒变形体的预测预警提供一定的参考,若发生库水位的骤升、骤降以及暴雨,需要进一步研究。
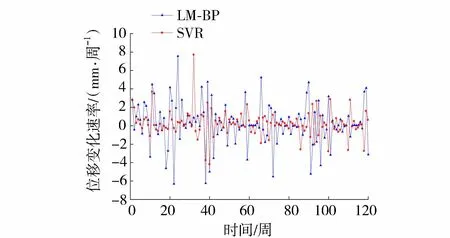
图7 监测点GTP06累积位移变化速率曲线Fig.7 Change rate curve of cumulative displacement for monitoring point GTP06
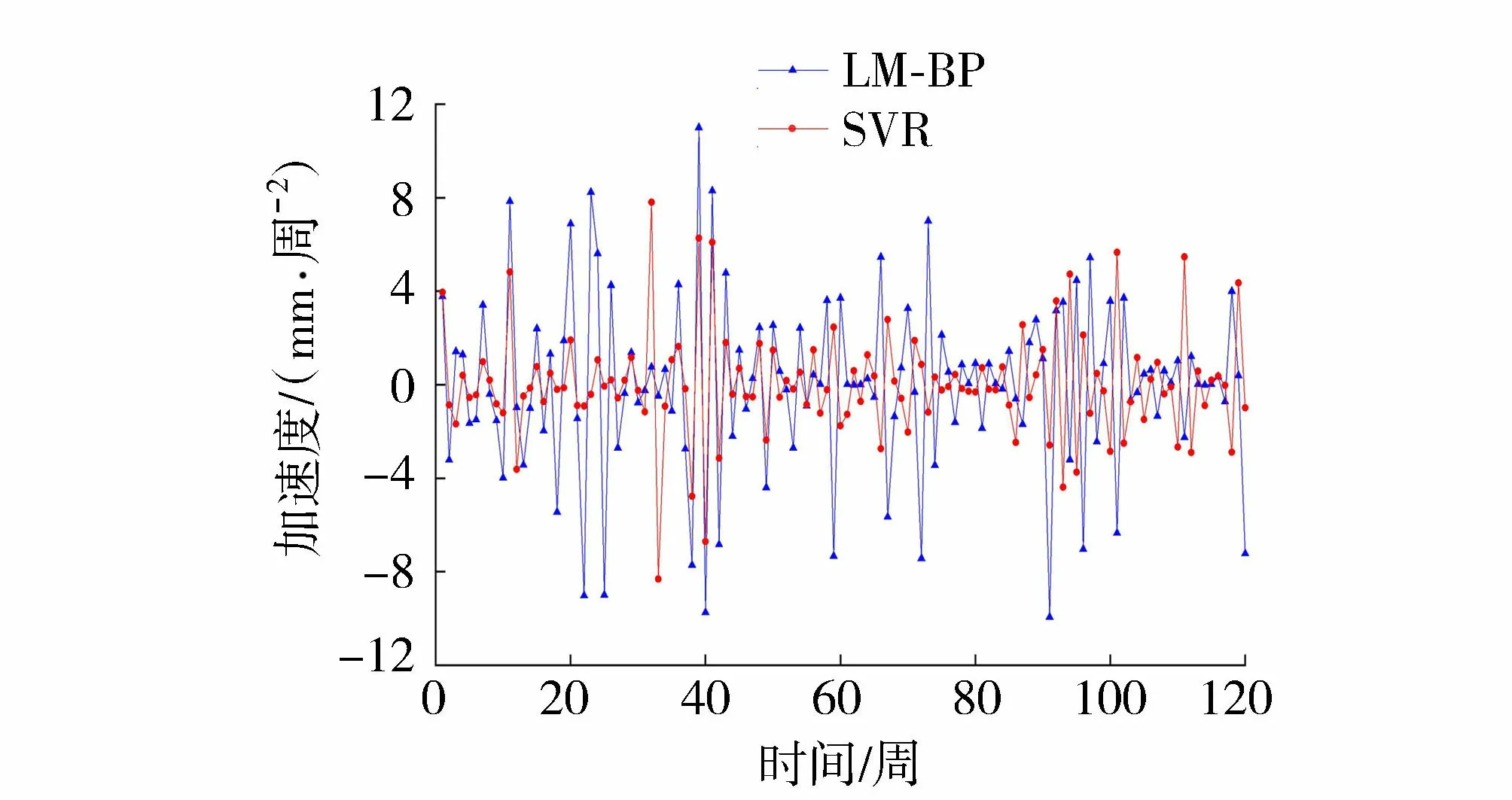
图8 监测点GTP06累积位移加速度曲线Fig.8 Acceleration curve of cumulative displacement for monitoring point GTP06
4 结 论
a.1号倾倒变形体的变形受水动力作用的控制,工程地质条件、降雨、库水位变化、温度和时间等因素均有影响。工程地质条件主要决定了倾倒变形体变形发育的总体趋势,降雨、库水位等诱发因素与其变形发育密切相关,降雨、库水位变化特别是水位骤降加速了1号倾倒变形体的变形破坏,变形与降雨、库水位变化的响应表现出一定的滞后性。
b.考虑到倾倒变形体受水动力作用的显著影响,应用LM-BP神经网络与SVR方法,以库水位变化、降雨量、温度、时间作为影响因素输入参数,以倾倒变形体的变形特征量作为输出参数,建立LM-BP神经网络模型和SVR预测模型。
c.基于LM-BP神经网络模型与SVR模型,对倾倒变形体的变形特征进行预测预报研究,结果表明,在黄登水电站正常运行调度工况下,LM-BP神经网络模型的最大误差为2.53%,SVR模型的最大误差为4.35%,2个模型精度都较高,LM-BP神经网络模型的精度比SVR预测模型更为精确,预测有效;目前黄登水电站近坝库岸1号倾倒变形体变形尚未收敛,需持续关注,加强监测预警、水位运行调度管理和风险分析。

