基于pOTM方法的超高速碰撞并行数值模拟研究
张天龙,马天宝,郝 莉
(1.北京理工大学 爆炸科学与技术国家重点实验室,北京 100081;2.北京建筑大学 理学院,北京 100044)
自20世纪60年代以来,随着航天事业的快速发展,太空碎片也随之增多。而这些大部分位于近地轨道的太空碎片相对于航天器的速度可达10 km/s以上,其极大的动能可以对在轨航天器造成非常严重的威胁。由于太空碎片体积小、数量大,大部分航天器采用加装Whipple[1-2]防护屏的方式来防护太空碎片。对于超高速碰撞问题,用理论分析方法建立一个普适的动力学理论模型需要涉及到多种领域,目前很难实现;现有的实验技术也很难达到所需要的环境;因此采用数值模拟方法研究超高速碰撞问题成为当下一种重要的方法。
对于超高速碰撞问题的数值模拟研究,无网格法因其自身的优势成为解决问题的主要方法。由Lucy等[3-4]提出的光滑粒子流体动力学方法,是目前最广泛使用的方法。然而SPH方法在超高速碰撞问题中,仍具有一定的缺点和局限性。其主要问题在于插值函数不满足Kronecker-delta属性,无法直接施加唯一边界条件,缺乏有效的数值积分方式,具有严重的零能模式以及拉力不稳定性问题等。
近十年来发展了一种新的数值方法,最早由M.Ortiz等[5-6]提出的一种显式增量更新拉格朗日无网格计算方法,最优输运无网格方法(Optimal Transportation Meshfree method,OTM)。相比于SPH方法[7],OTM方法集合了拉格朗日方法和无网格法的所有优点:质量守恒自动满足;边界处满足Kronecker-delta属性;插值和积分在不同的离散点上进行,避免了拉力不稳定性问题。本文采用pOTM方法模拟弹丸超高速正撞击单层靶板过程,通过与文献[8]结果进行对比,验证pOTM方法模拟超高速碰撞问题的适用性,同时分析了不同量级规模模型以及不同核心数对CPU并行计算耗费时间的影响。
1 OTM方法基本理论
几何模型Ω0∝R3所经历的一般力学过程由变形映射进行描述。假设变形梯度为
F=FeFp
(1)
式中:Fe表示弹性变形;Fp表示塑性变形。因此系统的内能密度可表示为
W=We,vol(J)+We,dev(FFp-1)+Wp(Fp)+Wh
(2)
式中:J=detF为变形梯度的Jacobian,We,vol与We,dev分别为弹性响应的体积部分和偏离项,Wp是塑性响应,Wh是热储量。从而可以推出以下变分结构:
(3)
式中:K是动能密度;B是单位质量体积力;T是施加于边界Γt上的牵引力。通过对等效势能Φ取变分可以获得线性动量守恒方程和能量守恒方程,即:
δΦ=0
(4)
1) 时间离散。从变分原理出发,对变分结构Φ取极值,再进行时间离散。对于给定的[tn,tn+1],若tn时刻的变量{φn}已知,则tn+1时刻的变量{φn+1}可以通过最小化增量近似获得,即:
(5)
采用后向差分格式进行近似,可以得到以下增量变分结构:
(6)
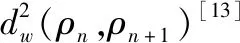
2) 空间离散。OTM方法采用两套粒子(物质点与节点)对几何模型进行空间离散。其离散方案如图1所示。
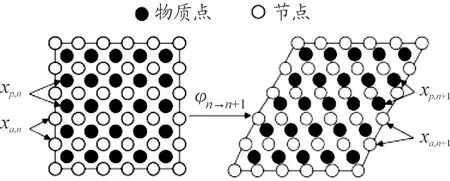
图1 物质点与节点空间离散方案示意图
在tn→tn+1过程中,物质点的更新通过邻域节点信息进行插值获得。则位移传输映射φn→n+1可以表示为
(7)
式中:N表示离散域内的总节点数;φa表示构形中节点的位置;Na(x)表示节点xa的插值函数[7]。同样地,物质点xp在tn+1时刻的位置xp,n+1及其变形梯度Fp,n+1可近似为
Fp,n+1=▽φn→n+1(xp,n)Fp,n
(8)
通过上述无网格离散方案,可得到全局系统的力平衡方程,即:
(9)

因此,节点xa在tn+1时刻坐标的更新形式为
(10)
式中:Ia,n为节点xa在tn时刻的线性动量,即:
(11)
通过求解每个节点的力平衡方程式(9),即可获得系统的整个位移变形场。
2 并行计算
在OTM方法求解过程中,其计算负荷主要集中在节点力的求解以及物质点邻域的更新及其相应的节点插值函数与导数的计算。由于其计算主要集中在物质点上进行,各个物质点之间没有相应的数据交换,所以此方法非常适合进行并行化计算。
pOTM是一种基于多核心并行化架构的大规模并行计算方法,利用Fortran语言通过MPI[9]编写了一套基于共享节点的划分方案,将求解模型进行分布式计算分解。
2.1 离散域分区
在pOTM方法中,首先将物质点划分成不同的子集分配到各个子核心中进行分布式计算,具体划分如图2所示。通过计算tn时刻PI子核心中各物质点的邻域,得到各个子核心所需要的邻域范围,把这个称为Range Box[10]。 Range Box中包含PI子核心中所有物质点的邻域范围内的节点。不同Range Box之间重叠部分被定义为Shadow Box,处于Shadow Box中的节点被定义为共享节点,其数据信息存储于共享数据交换表中。

图2 各核心物质点与节点划分示意图
2.2 数值迭代流程

(12)

根据更新后物质点邻域Np,k+1,更新各子核心PI其tn+1时刻的Range Box,然后判断时间步,若tn+1=tk,代表计算结束,得到t0→tk时间段内物质点和节点的动力学信息;若tn+1≠tk,则进行下一步迭代,直至tn+1=tk为止。
pOTM方法的主要求解过程可以描述为:
1) 将d维几何模型Ω0进行单元划分,将其离散为一组初始的节点集{xa,0,a=1,2,…,N}和一组初始的物质点集{xp,0,p=1,2,…,M};
2) 在初始时刻n=0时,初始化物质点坐标xp,n和节点坐标xa,n,将物质点集划分成不同的子集并分配到各个子核心中,初始化各子核心的Range Box以及相应的节点插值函数Na(xp,n)以及节点插值函数导数(Na(xp,n);

4) 根据节点坐标xn+1,此时节点产生位移,同时物质点将产生变形。利用局部最大熵插值函数计算物质点的局部增量变形梯度Fp,n→n+1=xa,n+1⊗▽Na(xp,n)和变形梯度Fp,n+1=Fp,n→n+1∘Fp,n来计算物质点的变形;
5) 根据第4步得到物质点从tn→tn+1时刻的运动和变形,更新物质点坐标xp,n+1、体积νp,n+1=det (Fp,n→n+1)νp,n以及密度ρp,n+1=mp/vp,n+1,其中mp为物质点质量;
6) 根据第4步和第5步得到的数据,通过本构关系获得物质点的应力σp,n+1,其中应力偏张量由Jaumann应力率模型给出,应力球张量由物质点的密度ρp,n+1通过状态方程给出;
7) 根据tn+1时刻下物质点xp,n+1的邻域以及节点坐标xa,n+1,更新各个子核心的Range Box,以及其相对应的节点插值函数Na(xp,n+1)及其导数(Na(xp,n+1);
8) 完成第7步后,即代表完成了物质点和节点在一个时间步内的动态分析,判断当前时间步n,如果已计算至最后一个时间步则结束计算,否则转入第3步。
3 弹丸超高速碰撞数值模拟
3.1 计算模型及材料模型参数
采用pOTM方法模拟球形弹丸超高速正撞击单层靶板的过程。模型结构中球形弹丸的直径为1 cm,撞击速度为6.18 km/s,单层靶板的尺寸为5 cm×5 cm×0.4 cm,球形弹丸和单层靶板的材料均为铝,其密度取为2.78 g/cm3。具体离散方案如图3所示。

左侧为局部放大图,空心为物质点,实心为节点
本构模型采用Johnson-Cook材料损伤模型[11],它可以描述在高温、高压、高应变率情况下金属材料的强度极限以及失效过程,即:
(13)
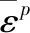
而Johnson-Cook材料损伤模型中的断裂由以下累积损伤定律导出:
(14)

对于状态方程,本文选用了较为常用的Mie-Grüneisen状态方程,其表达式为
p(ρ,e)=pH+Γρ0(e-eH)
(15)

其本构模型及状态方程的具体参数如表1和表2。数值工况参照Hiermaier[8]的实验数据。
3.2 网格收敛性验证
采用pOTM方法模拟球形弹丸超高速正撞击单层靶板的过程,分析不同网格密度模型规模下碎片云的形态。图4为20 μs时,不同网格密度模型规模模拟结果。

表1 Johnson-Cook损伤模型参数
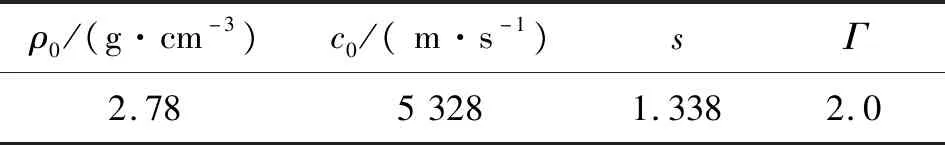
表2 Mie-Grüneisen状态方程参数

图4 不同网格密度模拟结果
从图4可以看出: 当模型规模偏少时,其碎片云形状比较不规则;随着模型规模的增大,碎片云形状开始变得更加圆润,且与实际效果吻合得更好。
假定布点密度为网格密度模型规模之比的三次方,且10万量级模型规模的布点密度为1,则可以得出相应的布点密度对碎片云具体参数的影响,如表3所示。
表3中,l为碎片云长度,w为碎片云宽度,Δ为相对误差。由表3可得,对于布点密度大的模型,碎片云的基本参数变化不大,误差在1.5%左右。因此可以认为在保证足够规模的网格密度下,计算结果随布点密度的增加趋于稳定。同时也可以在保证计算精度的前提下,适当减少布点密度来降低计算压力和加快计算速度。
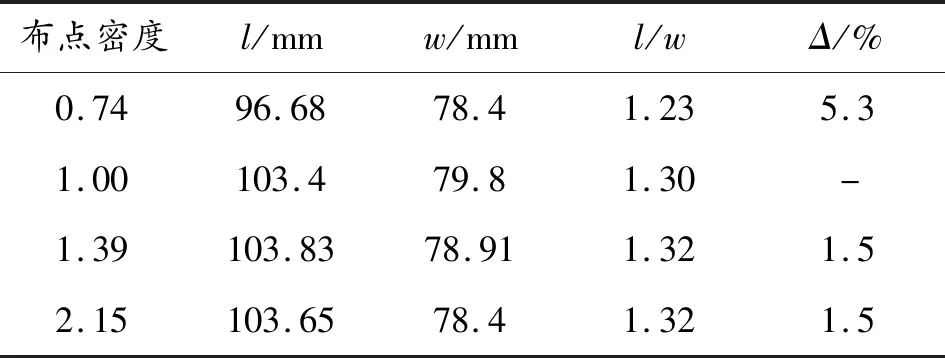
表3 碎片云的具体参数
3.3 结果及分析
通过高性能计算机集群进行并行模拟计算,采用24个核心数,计算模型被离散为45 634个物质点和58 916个节点,其数量级约为10万量级,其中弹丸包含5 704个物质点和7 366个节点,单层靶板包含39 930个物质点和51 550个节点,时间步长由CFL条件决定。图5是球形弹丸超高速正撞击单层靶板过程中,5 μs、10 μs、15 μs以及20 μs时刻碎片云的演化结果。图6是20 μs时刻碎片云的速度云图(撞击方向)和密度云图。
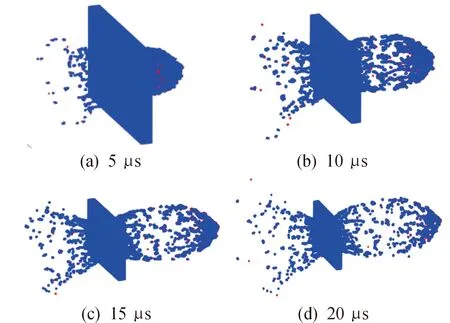
图5 pOTM方法模拟碎片云的演化过程

图6 20 μs时刻碎片云的速度云图和密度云图
取其20 μs时刻的演化结果与文献[8]结果进行对比(图7),本文所模拟得到的结果,靶板前端有明显的碎片飞溅,靶板后方的大部分碎片云质量集中在碎片云前端中轴线附近,得到的结果和文献[8]的结果吻合较好。
表4为采用pOTM方法模拟弹丸超高速正撞击单层靶板以及文献[8]结果的碎片云具体参数对比。
表4中,dc为靶板弹坑直径,Δ为l/w与实验结果的相对误差。综合表3、表4可以得出,pOTM方法模拟结果碎片云形态比较圆润,与文献[8]相比其相对误差比较小,且与实际结果吻合较好[12],比较适合对超高速碰撞问题进行深入研究。
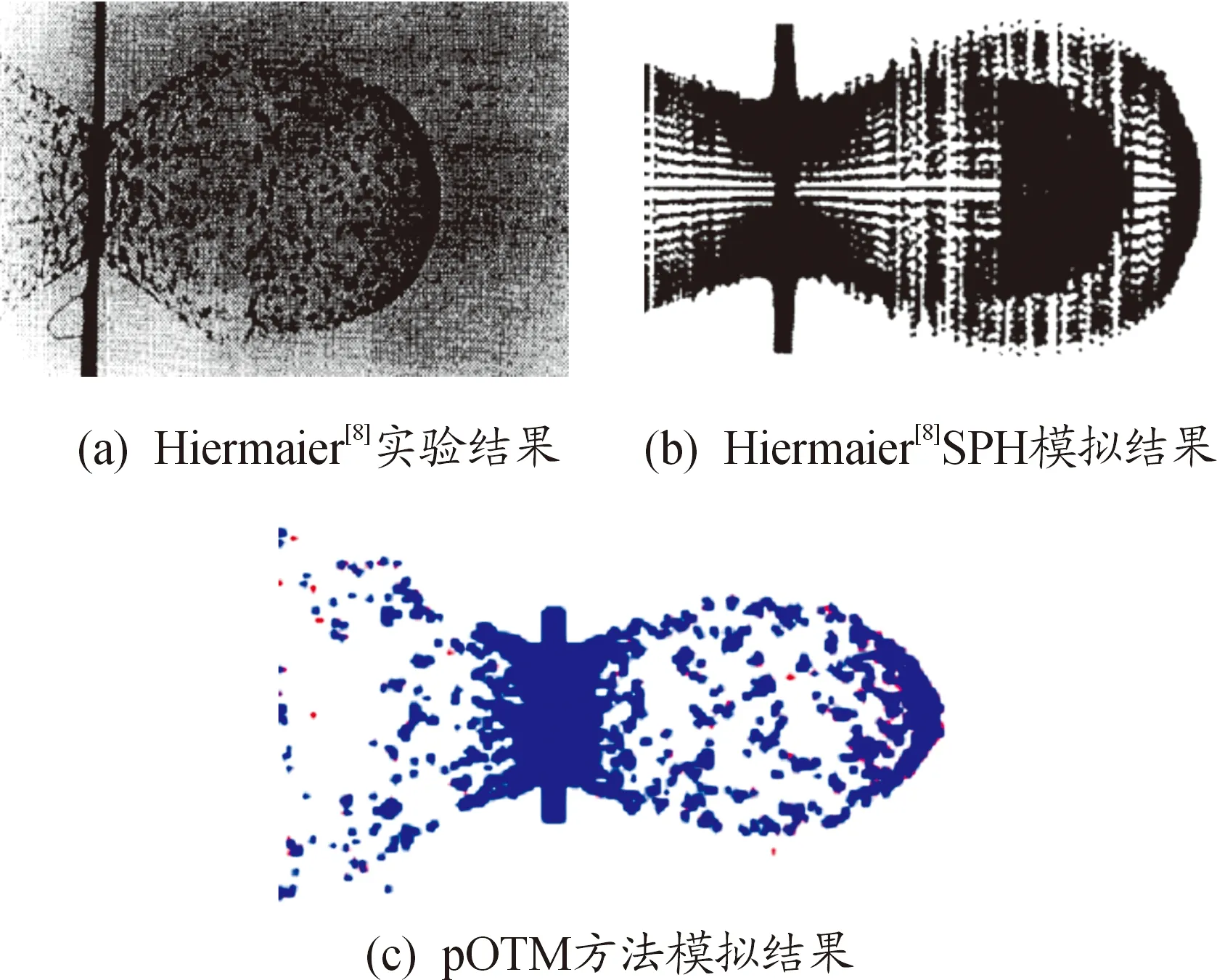
图7 不同数值方法模拟结果与实验结果对比

表4 碎片云的模拟结果
3.4 并行效率分析
采用pOTM方法在高性能计算机集群上对弹丸超高速正撞击单层靶板进行并行模拟研究,对比了不同核心数、不同物质点数和节点数下的多次并行计算结果,分析迭代 1 000 个循环所需要耗费的CPU时间,得到运行时间随核心数变化情况。图8为58 916个节点以及45 634个物质点迭代1 000个时间步耗费的时间随核心数的变化情况,其数量级约为十万量级。图9为638 196个节点以及50 3762个物质点,其数量级为约百万量级。
随着核心数的增加,计算所耗费的时间将逐渐减小,但是核心过多会导致MPI通信时间增加,从而导致整体计算时间增加。因此存在一个核心数使得并行计算耗费的时间最少。
对于十万量级的计算,其串行迭代1 000个时间步需要耗费7 975 s,使用24个核心进行并行计算,迭代1 000个时间步需要耗费624 s,其加速比[13]约为7 975/6 240=12.79,效率约为12.79/24=53.3%。

图8 十万量级计算时间随核心数变化图

图9 百万量级计算时间随核心数变化图
对于百万量级的计算,使用24个核心进行并行计算,迭代1 000个时间步需要耗费7 336 s,其加速比约为11.5,使而用28个核心需要耗费7 280 s,其加速比约为11.6。因此,虽然继续增加核心数,耗费的时间可以继续减少,但是减少的幅度变得很小,没有了实际意义。
因此对于十万量级的来说,采用24个核心数计算求解时,其加速比可以达到12.79,且随着核心数的增加,加速比不会产生明显的提升。对于百万量级,采用28个核心时,其加速比为11.6,其并行所耗费的时间可以降到最低。
从上述2个结果分析可以得出,如果模型规模在百万量级之下时,可以提供最多为13的加速比,即并行计算所耗费的时间为串行计算所耗费时间的1/13。因此本并行程序可以很大程度上节省CPU计算时间。
4 结论
1) 在弹丸超高速正撞击单层板把的数值模拟中,采用pOTM方法模拟所得到的结果与文献[8]中的实验和模拟结果吻合较好。结果显示碎片在单层靶板前端有明显的飞溅,靶板后方的大部分碎片云质量集中在碎片云前端中轴线附近,且靶板后方外围的碎片云质量分布比较均匀。弹丸超高速正撞击单层靶板所形成的弹坑直径以及碎片云的具体参数均与文献[8]中的结果相差无几,说明pOTM方法很适合来进行求解超高速碰撞相关的数值模拟问题;
2) 针对不同量级模型规模以及不同核心数对并行效率的影响,对十万量级以及百万量级的模型规模进行了分析,取其迭代1 000个时间步所耗费的CPU时间进行比较,结果显示,计算所耗费的时间会随着核心数的增加逐渐减小,但是核心过多也会导致通信时间的增加,因此存在最优核心数,对于百万量级28核心数为其最优核心数,其加速比可以达到12,可以很大程度上节省CPU计算时间。

