基于三点重合算法的飞机活动面转角测量研究

段曙凯,李徐辉,吴 熙,潘智昊

(上海飞机制造有限公司，上海 201324)

0 引言

飞机在空中飞行的姿态是通过飞机活动面转动来控制的，为了验证活动面的转动是否符合要求，需要对活动面的转动角度测量。飞机活动面的转动角度主要有这些方式：线位移测量方式[1]、角度尺测量方式[2]、MEMS陀螺仪测量方式[3]、拍摄测量方式和激光跟踪仪测量等方式。其中线位移测量方式需要确定测量点或传感器安装点的位置，该位置的测量误差会导致角度的误差。角度尺测量方式是在活动面上安装角度尺进行测量，这需要注意角度尺的转轴要与活动面的转轴平齐，这种方式由角度尺安装导致的误差较严重。MEMS陀螺仪测量方式是对转动加速度进行二次积分得到角度，借助重力进一步修正[4]，相当于倾角传感器来测量[5]。但对于方向舵这种转轴比较垂直的活动面[6]，修正效果不佳，使得测量精度不佳。

拍摄测量方式[7]和激光跟踪仪测量[8]方式都是在活动面上取样点，对样点的空间坐标进行处理得到转动角度。由于这两种测量方式在测量空间位置的精度都很高，其得到的角度精度也很高。本文主要探讨从样点数据中计算得到活动面的转动角度的方法，并提出一种计算角度精度较高的算法。

1 二面夹角问题

二面夹角问题是指活动面的转动角度，不一定是活动面上某个平面转动前后法线的夹角，其根本原因是刚体转动角度不能由该刚体内某平面的转动角度来表征。通过拍摄测量方式或激光跟踪仪方式来测量活动面的转动角度，首先必须获得一定数量的活动面的样点。通过这些点构建刚体，活动面的转动角度就是该刚体的转动角度。下面详细分析活动面刚体的转动角度与该刚体内某一平面的法线变化角度的区别。

通过拍摄测量或激光跟踪仪在活动面上采集一组样点，如图1左侧图所示。由于活动面是刚性的，可采用刚体内任意平面表征刚体的转动。

图1 平面表征刚体的运动

需要注意的是面A0B0C0转动到面A1B1C1的角度并非是面A0B0C0与面A1B1C1的夹角[9-10]，除非两个面的法矢与转动轴垂直。也就是说，二面夹角不一定是转动的角度。如图2所示，活动面绕某个轴转动，n0是平面A0B0C0的法矢，n1是平面A1B1C1的法矢。将平面A0B0C0随着中心的平移和n0的直接转动，到平面A1B1C1是在A0’,B0’和C0’的位置，并不和A1,B1和C1重合。这是因为选取的平面其法矢不与转动轴垂直所致。

图2 二面夹角不一定是转动角

活动面的转动可分解成法矢的转动和以法矢为轴的转动。由于活动面是曲面的，基本不可能选择到这样的平面，其法矢与活动面转轴垂直。在文献[2]中描述的方法是先确定平面与其转轴的夹角，通过前后平面夹角、平面与转轴夹角以及实际活动面转动夹角之间的关系计算实际平面的转动夹角。这种方法的应用需事先确定选取平面与转轴的夹角，对测量的操作要求较高。本文提出一种重合算法得到活动面的转角，适用于随机选取平面的测量方法，这种测量方法效率会有很大的提高，同时通过重合算法精度也得以保证。

2 三点分步重合

基于上述分析，不能直接用二面夹角来表征活动面的转角。因为两个平面的重合不一定是刚体的重合，但平面的三角面片的重合就可以决定两个刚体的重合。当然重合的时候需要注意方向，因为三角面片的重合会导致刚体两个方向的重合，即三角面片正反面的重合，但只有一个方向可使得刚体完全重合，后续会详细介绍。三角面片的重合无法一步到位，需将三角面片内三个顶点分步重合。三点重合算法就是三角面片的三个顶点分步重合，通过该算法计算得到三角面片转动角度，从而计算活动面刚体的转动角度。以图1的三个顶点为例，下面描述该分步重合的过程。

将A0B0C0和A1B1C1单独取出，先通过平移，将A0重合到A1上，同时B0平移到B0’上，C0平移到C0’上。这是第一个点的重合，该重合只是平移，没有旋转。如图3所示。

图3 第一点的重合

将B0’绕A1点转动到B1点上，此时C0’转动到C0’’上，如图4所示。这个转动是直线定点转动，旋转轴线是两条直线形成的平面的法线，转动角度是两条直线的夹角。

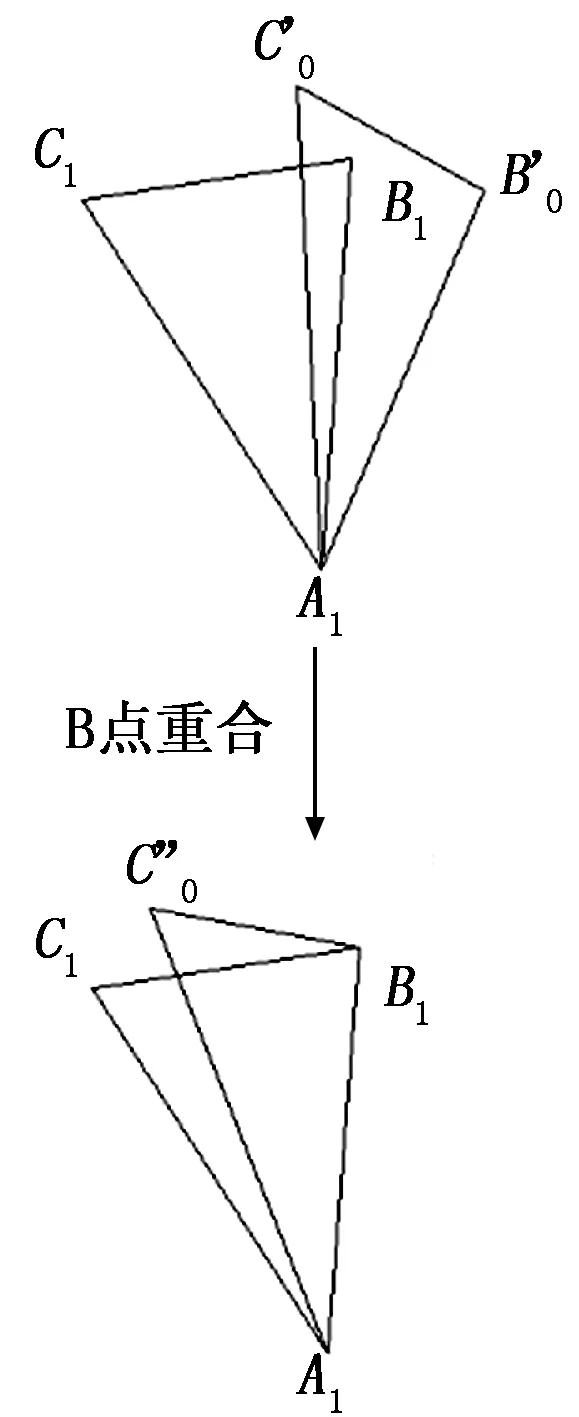
图4 第二点的重合

A点的重合过程和B点重合过程可以合在一起用式表示：

对照组：入院确诊后均给予常规饮食控制、运动疗法、口服降糖药或皮下注射胰岛素降低血糖，给予降血压、调脂、改善肾脏微循环等治疗，在此基础上，给予盐酸贝那普利片治疗，口服盐酸贝那普利片30 mg/次，1次/d。观察组：在对照组的治疗措施基础上给予补肾活血汤治疗，处方：黄芪60 g，党参、熟地黄、茯苓、炒山药、枸杞子、鬼箭羽、蒲公英各15 g，山茱萸、泽泻和补骨脂各 12 g，砂仁 10 g，甘草 6 g，水蛭粉（冲服）3 g，1剂/d，煎汁300 mL分成早晚两次饭后温服。两组患者均连续治疗3个月。

B1-A1=(B0-A0)·MB

式中,MB是B点重合过程的旋转矩阵，即矢量A1B1旋转到A0B0。旋转轴是直线A1B1与A1B0’形成的平面的法线。由于A1B0’是A1B1平移所得，其两条直线的矢量是相同的，所以旋转轴矢量nB为:

转动角θB为直线A1B1与A1B0’的夹角，也就是A1B1与A0B0的夹角的余弦值为:

根据罗德里格斯公式可得旋转矩阵MB:

C0’’-A1=(C0-A0)·MB

最后一步就是C的重合，也就是C1与C0’’重合，这个过程需要将A1B1C0’’绕A1B1轴旋转到A1B1C1，如图5所示。

图5 第三点的重合

旋转角度为A1B1C0’’与A1B1C1的夹角，即两个面的法线夹角。A1B1C1法线n为:

n=A1C1×A1B1

A1B1C0’’的法线n’为:

n’=A1C0’’×A1B1

需要注意，参与计算n与n’的A1C1与A1C0’’方向必须是同时是A到C，或者同时是C到A。转动角度的余弦值为：

A1B1C0’’旋转到A1B1C1的旋转轴矢量为：

需要注意的是旋转轴矢量的方向，也就是式中的正负号。三角面片的重合会使得刚体由两个方向的重合，正面和反面重合，也就体现在n的正负号上。在直线AB上任取一点D，连接出两条径向矢量DC1与矢量DC0’’，如图6所示。矢量DC0’’转动到矢量DC1的旋转轴矢量为nD=DC0’’×DC1。

图6 第三点的重合

无论D在直线AB哪个位置，C点重合所绕的旋转轴矢量nC与nD的夹角是锐角，才能保证右手旋转方向规则。将D选在A这个位置也满足要求，因此也必须要求旋转轴矢量nC与A1C0’’×A1C1成锐角。即：

根据罗德里格斯公式可得旋转矩阵MC:

使B点重合的矩阵为MB，使C点重合的矩阵为MC。两个矩阵的合成为M，该M即为活动面刚体的旋转矩阵。

M=MBMC

所以旋转角度为:

式中,θ是三点分步重合的角度，也是活动面转动的角度，tr(R)是矩阵R的迹。

三点分步旋转重合是三角面片的重合过程，通过该过程得到三角面片的重合角度，也就得到活动面的角度旋转角度。三点分步的第一步是先平移是某个点在运动前后位置重合。再绕已经重合的点将另一点旋转重合，这样面片的一条线段也重合。最后，以该线段为旋转轴，将另一点旋转重合。两次旋转重合对应的旋转矩阵相乘即得到最终的旋转矩阵，通过该旋转矩阵得到最终的转动角，也就是活动面的转动角。这就是三点重合算法的大概过程。

3 误差与三点选取

三点分步重合算法的精度依赖于选取的三个点，由于点位测量会有一定的误差，如果选取的点能将这些点位误差对角度的影响降到最低，那么三点分步重合算法的精度就最高。在径向上选取两点A和B，运动前A和B分别在A0和B0的位置上，运动后A和B分别在A1和B1的位置上。将这些点向垂直于转动轴的平面投影，并将B0和B1重合，如图7所示。

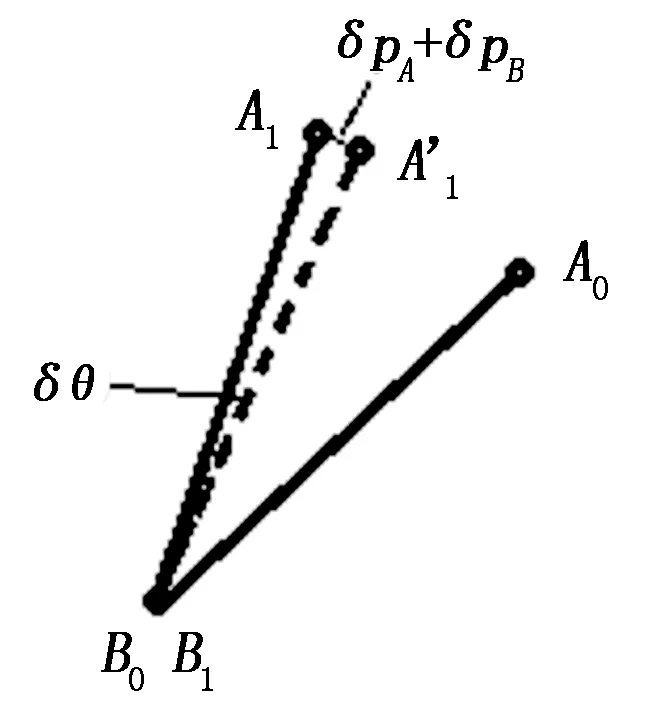
图7 误差分析示意图

A’1是A运动后的实际位置，A1是测量的位置。A1与A’1之间的误差既有A点测量的误差，又有B点测量的误差，即为δpA+δpB。该误差所导致角度的误差与该误差的关系为:

式中,d为A和B的距离。可知在径向上，如果选取两点的径向距离越大，其位置误差引起的角度误差越小。众所周知，若一个点离转动轴越远，同一个角度下，其运动的距离也就越大。若一个点离转动轴越近，同一个角度下，其运动的距离也就越小。因此径向方向上两点的选取可以通过运动位移作为选择最佳两点的标准。通过该标准，选取位移最大的和位移最小的两个点。

基于以上分析，设计如图8的寻找最优两点的程序。程序流程图中的i是点的编号，pi是点i运动前的坐标，qi是运动后的坐标。di是编号i的点运动前后的距离。dmax是用于存储当前所遍历到第i个点时发现的最大运动距离的变量，dmin为存储发现的最小距离的变量。该程序最后输出的是运动最大距离的点的编号和运动最小距离的点的编号。

图8 最优两点的搜寻流程图

可在轴向上选取一点，根据同样的原理，如果C点离A和B的距离最远，如图9所示，那么C点测量的位置误差对角度误差影响最小。也就是说如果点A、点B和点C形成的三角面片的面积最大，那么位置误差对角度误差的影响最小。

图9 最优第三点的位置

三角形ABC的面积计算如下:

S=|AB×AC|

使S最大点就是选取的第三点C。

4 试验结果与分析

为验证三点分步重合算法的精度，进行精度验证试验。采用转台作为实际的转动角度基准。在转台上设置两个面，一个是曲面，一个是平面。平面的法线与转台转动轴线垂直，曲面可以形成与转台轴线不垂直的面。转台在-25到25度之间运动，每5度测量三次。为了样点测量方便，采用拍照测量方式。即在平面和曲面上事先贴上标记点，再通过这些标记点计算平面和曲面的转动角度，再与实际转台的角度进行对比，形成如下实验数据。

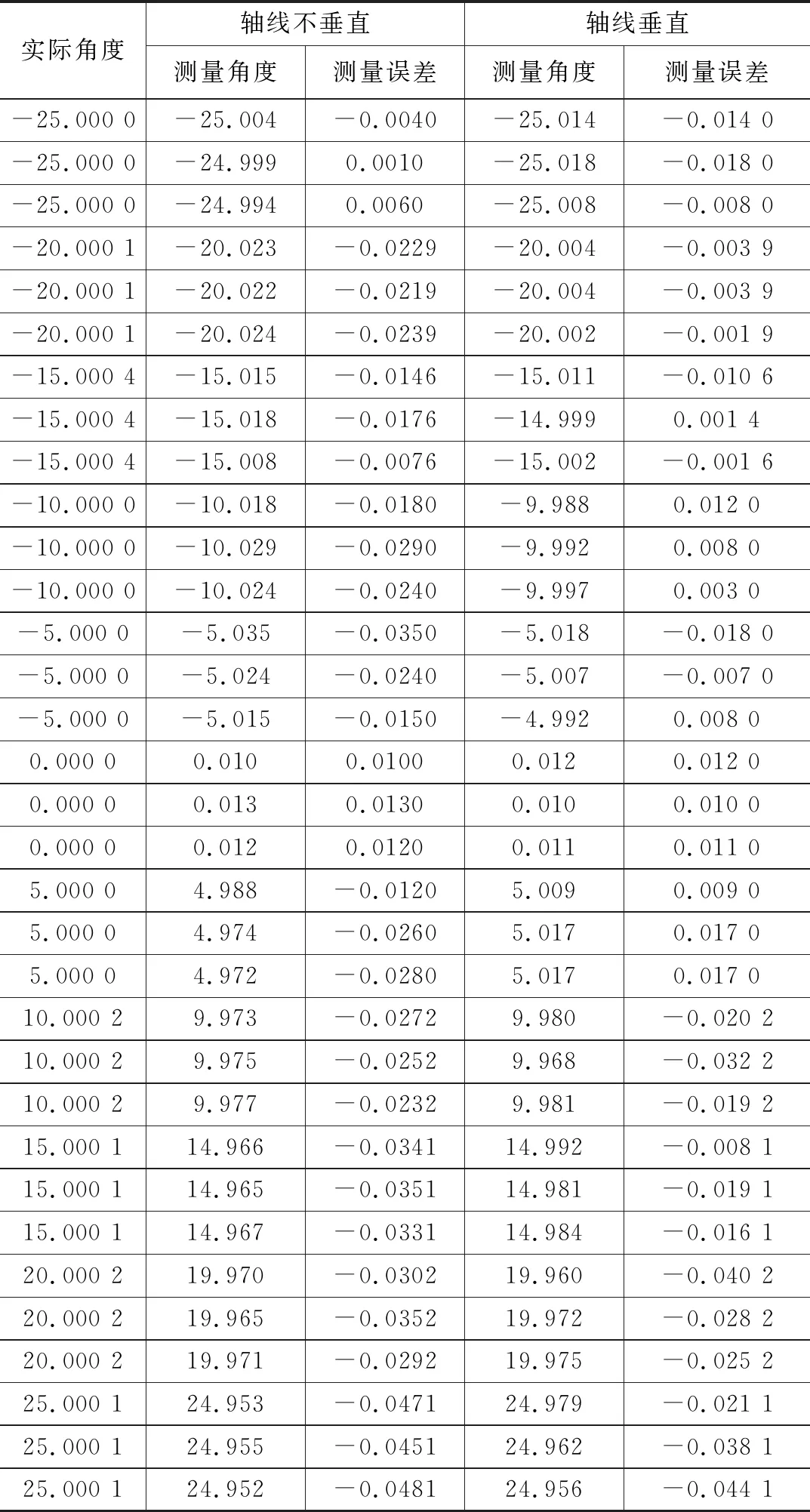
表1 精度验证实验数据 单位：度

从表1中可知，曲面样点计算的误差绝对值的平均值为0.023度，误差最大为-0.048 1，这是该算法用于轴线不垂直的情况；平面样点计算的误差绝对值平均值为0.015 3度，误差最大值为-0.044 1，这是该算法用于轴线垂直的情况。将每个角度的三个测量数据误差平均并取绝对值，可作图10的误差变化曲线。

图10 误差变化曲线

图10中，虚线为曲面样点计算(即轴线不垂直)的误差曲线，实线为平面样点计算轴线(即垂直)的误差曲线。从图10中可以看出，在轴线不垂直时的误差相对与轴线垂直的误差较大，随着角度增大误差也增大。前者的主要原因是轴线垂直重合过程两步即可完成，一步是平移，另一步是旋转；而轴线垂直不垂直时重合过程有三步，一步平移和两步旋转。随着角度增大误差也增大的主要原因是角度每一次增加会有一定的误差累积，该情况在很多算法中也会存在，是一个通病，可不作为衡量算法好坏的标准。通过本精度验证实验可知，本试验的三点重合算法的误差在0.05度范围内，该误差满足实际生产中飞机活动面的转角测量要求。

5 结束语

本文提出了一种三点重合的算法用于拍摄测量活动面角度或激光跟踪仪测量活动面角度，重合的过程是先平移是某个点在运动前后位置重合。再绕已经重合的点将另一点旋转重合，这样面片的一条线段也重合。最后，以该线段为旋转轴，将另一点旋转重合。两次旋转重合对应的旋转矩阵相乘即得到最终的旋转矩阵，通过该旋转矩阵得到最终的转动角，也就是活动面的转动角。

然后从原理上对误差进行分析，提出一种最佳选取三点的方法，即选取前后运动位移最小的点和最大点，再选取一点离之前两点连成的直线最远的点，这样可形成面积最大的三角面片，从而减少位移测量产生的误差对旋转角度计算上的误差。设计一种实验，该实验采用拍摄测量的方式，以快速取得多个样点。设置一转台，转台上设置一曲面与一平面，通过比较曲面样点计算的角度、平面样点计算得到的角度与转台实际转动的角度进行对比。该实验结果表明，本文所提出的三点重合的算法误差在0.05度范围内，满足飞机活动面的转角测量要求。