钢桥塔与塔吊联合体系抖振响应试验研究
马如进 李方宽 胡晓红 丁磊

摘 要:研究了自立状态钢桥塔与塔吊组成的联合体系的抖振性能及塔吊对钢桥塔抖振响应的影响. 通过钢桥塔与塔吊共同作用的联合气弹模型风洞试验与自立状态桥塔气弹模型风洞试验,识别出了两种体系的模态参数并获得了不同风速及不同风偏角下两种体系的抖振响应,对风速与风偏角的影响规律进行了总结与比较,对比研究了联合体系中塔吊与桥塔在顺桥向、横桥向的振动响应差异. 结果表明,钢桥塔与塔吊的风致抖振位移响应均值可以近似表示为风速的二次函数,位移响应均方差则表现出一定的波动性,塔吊会显著减小钢桥塔抖振位移响应的均值与均方差,钢桥塔与塔吊风致抖振响应存在明显的风偏角效应,塔吊的局部振动效应使得顺桥向塔吊位移相对桥塔位移存在明显的放大效应,而横桥向存在一定的缩小效应.
关键词:钢桥塔;塔吊;自立状态;抖振;风偏角;风洞
中图分类号:U448.36 文献标志码:A
文章编号:1674—2974(2021)01—0092—08
Abstract:In order to clarify the buffeting performance of the joint system composed of free-standing steel pylon and tower crane as well as the effect of tower crane on the buffeting response of steel pylon, wind tunnel tests of aeroelastic model of the joint system and free-standing pylon are designed and carried out. Modal parameters and buffeting performance under different wind speeds and wind yaw angles of the two systems are obtained. The effects of wind speed and wind yaw angle on the two systems are summaried and compared, and the vibration responses of the joint system between tower crane and steel pylon in both longitudinal direction and lateral direction are compared in the end. The results show that the mean value of wind-induced buffeting displacement of steel pylon and tower crane can be approximately treated as a quadratic function of wind speed, while the standard deviation of displacement oscillates back and forth with the increase of wind speeds, and the existence of tower crane can decrease the mean value and standard deviation of wind-induced buffeting displacement of steel pylon significantly. Wind yaw angle has obvious effects on the wind-induced response of steel pylon and tower crane. The vibration response of the tower crane is much larger than that of pylon in longitudinal direction of bridge, but it is a little smaller in lateral direction due to the local vibration of tower crane.
Key words:steel pylon;tower cranes;free-standing state;buffeting;wind yaw angle;wind tunnels
大跨度斜拉桥桥塔自立状态下缺少拉索的支撑作用,是施工过程中最不利状态之一. 已有文献表明,此时钢桥塔阻尼比一般为0.05%~0.35%[1-2],这种低刚度、低阻尼的特性使得钢桥塔施工期间的风致振动现象更加突出,通过改善气动选型和增设气动措施,桥塔在自立状态下的涡激共振和驰振问题已经可以得到解决,但是随机抖振现象是无法避免的[3]. 抖振是桥梁结构常见的风致限幅振动之一,可发生于桥塔[3]、吊杆[4]等主要构件,国内外学者对此开展了广泛的研究. 抖振一般不会引起桥塔结构的失稳或破坏,但过大的抖振响应会影响施工机械和工人的安全,还会引起桥塔结构的疲劳问题[5-6].
国内外相关学者针对桥塔自立状态下的抖振响应特性,采用数值模拟和风洞试验两种方法开展了一系列研究. 王统宁等[7]采用抖振时域分析方法计算了鄂东长江公路大桥桥塔的抖振响应. 周奇等[8]通过气弹模型试验对比研究了几种典型桥塔抖振响应与风偏角、横桥向结构形式、來流风速等因素的关系. 胡庆安等[9]进行了考虑塔吊共同作用的桥塔联合气弹模型风洞试验,并结合抖振时域分析方法研究了风速与风偏角对施工阶段桥塔抖振性能的影响. 车鑫等[10]通过风洞试验方法研究了港珠澳江海直达航道桥桥塔自立状态下的抖振响应随风速、风偏角的变化规律. 胡航[11]通过风洞试验验证了苏通大桥施工阶段主塔、塔吊联合体系抗风性能的安全性. Hernández等[12]对西班牙一座倾斜塔柱独塔斜拉桥进行了风洞试验,研究了塔柱施工时带有模板和塔吊的自立状态下的风致振动响应. Luo等[13]通过风洞试验研究了马来西亚槟城二桥桥塔自立状态下的各类风致振动响应,验证了施工期桥塔的安全性. Ma等[14]通过风洞试验研究了不同来流下周边建筑物对桥塔抖振响应的影响规律.
以上研究大部分是针对自立状态下的桥塔开展的,而没有考虑施工过程中塔吊对于桥塔周边风场的影响,虽然胡庆安等[9]、胡航[11]研究了桥塔与塔吊联合体系在斜风作用下的抖振性能,但没有针对塔吊关键位移进行相关的分析研究. 基于此,本文針对某独柱型全钢桥塔结构开展了考虑塔吊共同作用的桥塔联合气弹模型风洞试验,对紊流场中风速、风偏角对于自立状态下桥塔与塔吊联合体系以及自立状态桥塔风致抖振响应的影响规律进行了系统研究,比较得出了塔吊对于桥塔抖振位移响应的影响,研究方法和成果可为国内外相似结构形式的钢桥塔施工提供参考和借鉴.
1 工程背景
本文研究对象为南京浦仪长江公路大桥,该桥采用独柱型全钢桥塔,塔高166 m,其中桥面以上塔高130.7 m,施工时采用MD3600型塔吊,两道附墙将塔吊与桥塔相连,附墙高度分别为67.25 m和119.25 m,相应的塔吊、附墙与桥塔的关系如图1(a)所示. 上塔柱为6.5 m × 6 m带切角的矩形断面,下塔柱截面渐变至16 m × 9.5 m;塔吊吊臂长42.24 m,平衡臂长28 m,塔肢为直径0.18 m的圆形截面,四塔肢中心距5.5 m. 相应的平面布置图如图1(b)所示.
2 模型风洞试验
2.1 动力特性分析
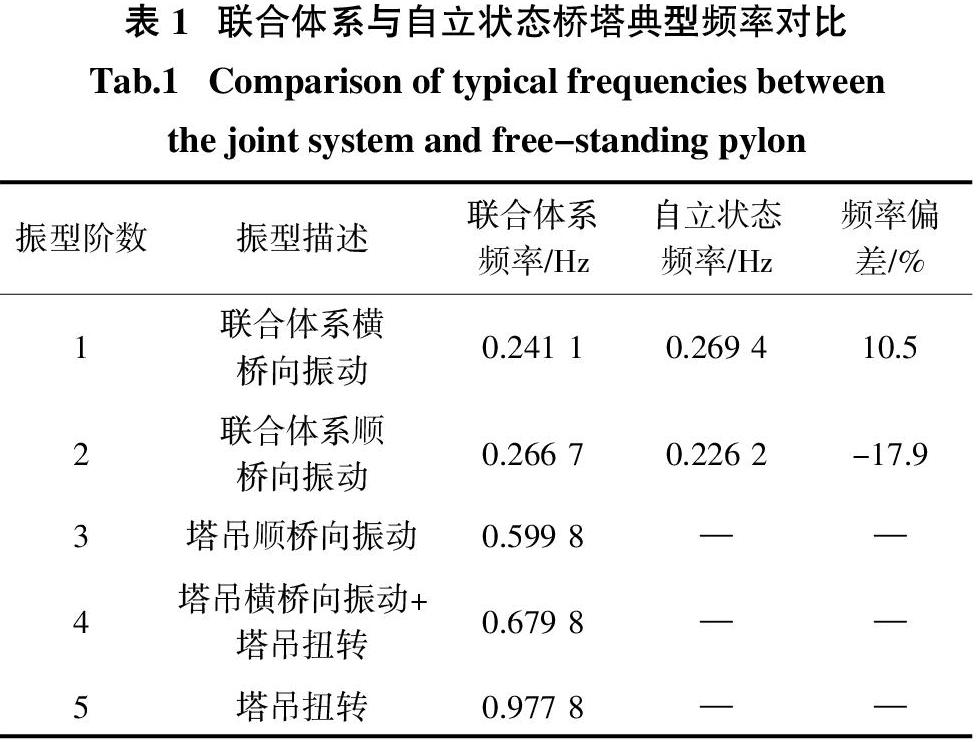
结构动力特性分析采用有限元方法进行,建立了联合体系及自立状态桥塔的有限元模型,桥塔及塔吊在承台处固结,其中桥塔、塔吊和附墙均采用梁单元模拟. 通过动力特性分析可以得到联合体系及自立状态桥塔典型频率如表1所示. 结果表明,联合体系以桥塔振动为主的1阶顺桥向弯曲(联合体系2阶振型)频率为0.266 7 Hz,1阶横桥向弯曲(联合体系1阶振型)频率为0.241 1 Hz;以塔吊振动为主的1阶顺桥向振动(联合体系3阶振型)频率为0.599 8 Hz,1阶横桥向振动(联合体系4阶振型)频率为0.679 8 Hz. 与之相比,自立状态桥塔1阶顺桥向弯曲频率减小17.9%,为0.226 2 Hz;1阶横桥向弯曲频率增大10.5%,为0.269 4 Hz.
与自立状态桥塔相比,塔吊会增大联合体系的刚度与质量,上述频率变化说明,在横桥向塔吊对联合体系质量的贡献作用大于对刚度的贡献,在纵桥向则相反. 另外,通过以上分析可以发现,塔吊的存在会对桥塔振动频率产生明显影响,因此,在桥塔自立状态下的风致振动响应分析中,塔吊的影响不能忽略,采用联合体系模型能更好地反映施工过程中结构体系的受力状态.
2.2 气弹模型设计及动力特性调试
试验在同济大学TJ-2边界层风洞中进行,按照试验相似关系并考虑到风洞试验段高度,设计气弹模型缩尺比为1 ∶ 100,自立状态桥塔模型高度1.66 m,塔吊模型高度1.94 m. 桥塔模型由铝芯、塑料外衣和配重构成,塔吊模型按照气动力相似与刚度相似原则,采用空心铜棒制作. 图2为置于风洞中的联合体系气动弹性模型,模型拼装完成后,对整体结构体系动力特性进行了检验,相应的模型频率和阻尼比测试结果见表2. 可见,联合体系模型前5阶频率误差均小于5%,相应阻尼比约为0.3%,自立状态桥塔模型前两阶频率误差均小于5%,相应阻尼比约为0.1%,均可以满足风洞试验要求.
2.3 试验布置及工况设计
试验采用尖塔和粗糙元模拟缩尺比为1 ∶ 100的桥位B类风场,紊流风场特性如图3所示,可以看出模拟风场满足规范要求,并在模拟风场中开展抖振响应测试. 考虑到塔吊与桥塔的振型特点,在桥塔塔顶与65%高度处各布置两个水平方向的位移传感器,塔吊悬臂端与塔吊顶部各布置两个位移传感器.相应传感器位置布置如图4所示.
定义来流方向为顺桥向且桥塔在上游时的风偏角为0°,由于塔吊布置在桥塔的一侧且考虑来流风向的影响,联合体系模型试验以15°为增量考虑了0° ~180°风偏角,共计13个试验工况. 由于对称性,自立状态桥塔模型试验考虑了0° ~ 90°风偏角,共计9个试验工况. 相应的风偏角与桥塔、塔吊联合气弹模型关系如图5所示.
3 试验结果分析
3.1 抖振响应随风速变化规律
针对不同风偏角下的试验结果进行分析,可以得到不同来流方向风速影响下的结构抖振响应特征. 本节以联合体系模型及自立状态桥塔模型在风偏角为0°和90°时的试验结果为例进行讨论分析.
图6给出了风偏角为0°时联合体系位移响应均值、均方差随风速的变化规律. 由于此时风向为顺桥向,所以重点考查联合体系顺桥向位移响应均值. 从图6(a)可以看出,桥塔顶部、塔吊顶部与塔吊悬臂端顺桥向位移响应均值均随风速的增大而逐渐增大,且变化趋势接近二次曲线规律;从图6(b)中可以看出,桥塔顶部、塔吊顶部与塔吊悬臂端顺桥向位移响应均方差在总体上均呈现出随风速增大而增大的趋势,并均表现出一定的波动性,且横桥向及塔吊悬臂端竖向的波动性更为突出.
图7给出了风偏角为90°时联合体系位移响应均值、均方差随风速的变化规律. 由于此时风向为横桥向,所以重点考查联合体系横桥向位移响应均值.
从图7(a)中可以看出,随着风速增大,桥塔与塔吊位移响应均值均呈现出先减小后增大的趋势,风速大于10 m/s时,桥塔顶部、塔吊顶部横桥向与塔吊悬臂端竖向位移响应均值随着风速增大而逐渐增大,且变化趋势接近二次曲线规律;从图7(b)可以看出,与风偏角为0°时相比,由于塔吊对桥塔周围流场的扰动性更强,桥塔顶部、塔吊顶部与塔吊悬臂端位移响应均方差总体上仍随风速增大而增大,但在变化过程中呈现出更为明显的波动特征.
作为对比,图8给出了风偏角分别为0°、90°时自立桥塔位移响应均值、均方差随风速的变化规律. 从图8(a)可以看出,桥塔顶部顺风向位移响应均值随风速的增大而逐渐增大,且变化趋势接近二次曲线规律,这与联合体系相似,但是在同一风速时自立状态下桥塔顶部位移远大于联合体系,以设计基准风速为例,自立状态桥塔顶部位移均值在0°风偏角工况下是联合体系的5.2倍,90°风偏角下是联合体系的3.7倍,这说明塔吊的存在会显著减小桥塔的位移响应.
从图8(b)中可以看出,桥塔自立状态下,桥塔顶部位移响应均方差随风速的变化规律与联合体系相似,总体上随着风速的增大而增大且表现出一定的波动性,同时可以看出桥塔自立状态下在同一风速时桥塔顶部位移均方差远大于联合体系,以设计基准风速为例,自立状态桥塔顶部顺桥向、横桥向位移响应均方差在0°风偏角工况下分别是联合体系的3.8倍、2.8倍,90°风偏角下则分别是联合体系的6.8倍、1.7倍,说明塔吊对流场的扰动作用会显著减小桥塔顶部位移响应均方差,这一效应在顺桥向尤其明显.
3.2 抖振响应随风偏角变化规律
根据《公路桥梁抗风设计规范》[15]得到施工阶段桥塔基准高度处设计基准风速为36.5 m/s. 本节探讨了设计基准风速下,联合体系抖振位移响应均值和均方差随风偏角的变化规律,主要试验结果如下:
图9给出了位移响应均值、均方差随风偏角的变化曲线. 从图9(a)可以看出,桥塔顶部顺桥向位移响应均值在风偏角为150°时最大,在风偏角为90°时最小;桥塔顶部横桥向位移响应均值在风偏角为75°时最大,在风偏角为180°时最小;整体而言,由于桥塔顺桥向刚度小于横桥向刚度,桥塔顶部顺桥向位移响应均值的最大值大于横桥向位移响应均值的最大值.
塔吊悬臂端顺桥向位移响应均值在风偏角为150°时最大,在风偏角为75°时最小;塔吊悬臂端横桥向位移响应均值在75°时最大,在风偏角为180°时最小. 整体上塔吊悬臂端呈现出与桥塔顶部相似的变化规律,但塔吊悬臂端顺桥向位移与横桥向位移最大值之间的差值比桥塔更为突出,这是由于塔吊悬臂端顺桥向位移由塔吊整体顺桥向位移与其悬臂端绕塔身扭转产生的顺桥向位移两部分组成,因此表现出比桥塔顶部顺桥向与横桥向之间更大的刚度差异.
从图9(b)可以看出,桥塔顶部顺桥向位移响应均方差在风偏角为105°时最大,在风偏角为45°时最小;桥塔顶部横桥向位移响应均方差在风偏角为30°时最大,在风偏角为150°时最小. 总体上风偏角相同时桥塔顶部顺桥向位移响应均方差小于横桥向位移响应均方差,表明桥塔顶部横桥向位移响应对于风的脉动成分更为敏感.
塔吊悬臂端顺桥向位移响应均方差在风偏角为15°时最大,在风偏角为135°时最小;塔吊悬臂端横桥向位移响应均方差在30°时最大,在风偏角为150°时最小. 整体上塔吊悬臂端位移响应均方差呈现出与桥塔顶部相似的变化规律,但是风偏角相同时塔吊悬臂端顺桥向位移响应均方差大于横桥向位移响应均方差,表明塔吊悬臂端顺桥向位移响应对于风的脉动更为敏感.
整体而言,尽管桥塔顶部、塔吊悬臂端在横桥向与顺桥向对于风的脉动成分敏感程度不同,但这种差异相对较小.
3.3 塔吊振动响应比例系数研究
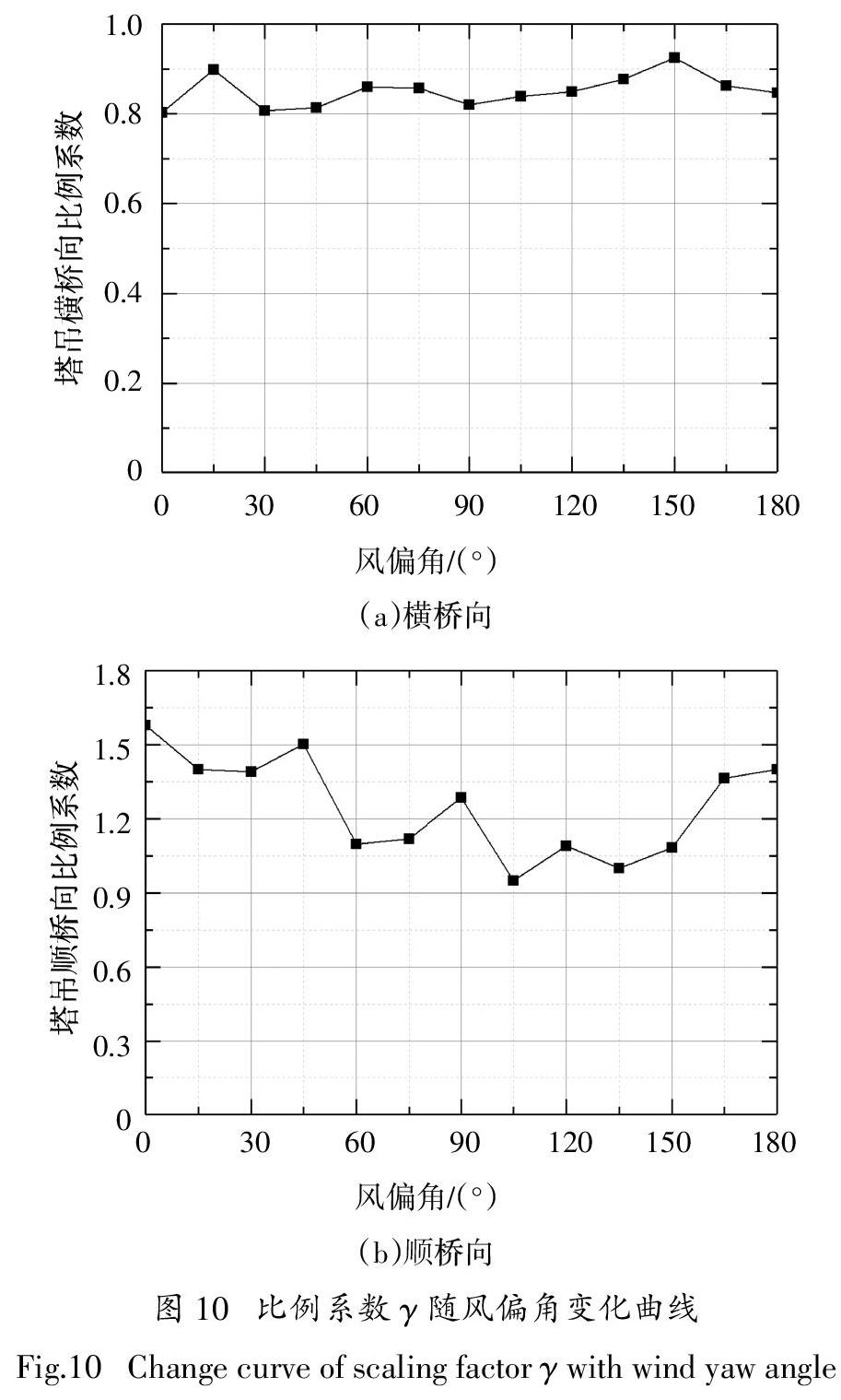
塔吊与桥塔形成联合作用体系,在风荷载作用下其振动响应存在一定的耦合特征. 为了比较塔吊与桥塔振动响应的相互关系,本节定义塔吊振动响应比例系数为γ = σ2 /σ1 ,用来表征不同来流方向风作用下塔吊与桥塔位移响应的差异,其中σ1为桥塔顶部位移响应均方差,σ2为塔吊位移响应均方差.
图10给出了比例系数γ随风偏角的变化规律.从图10(a)可以看出,横桥向比例系数γ (此时σ2对应塔吊顶部)主要在0.8~0.95范围内波动,在风偏角为150°时取得最大值0.93,在风偏角为0°时取得最小值0.80. 从图10(b)可以看出,顺桥向比例系数γ(此时σ2对应塔吊悬臂端)主要在1.0~1.6范围内波动,在风偏角为0°时取得最大值1.58,在风偏角为105°时取得最小值0.95.
不难看出,顺桥向塔吊振动响应比例系数相比横桥向存在明显的振动放大效应. 通过结构模态分析可以发现,对于顺桥向振动,联合体系一阶模态中塔吊与桥塔的幅值比为1.09,高阶模态中塔吊与桥塔的幅值比可以高达6.86,而横桥向模态分析结果没有发现幅值放大现象. 这也说明了,对于本桥的桥塔-塔吊联合体系平面布置方案而言,虽然顺桥向的第一阶频率与自立状态桥塔相比略有提升,但是由于高阶振型的放大作用,顺桥向塔吊悬臂端位移响应明显高于桥塔顶部位移响应,在施工过程中应该给以重点关注.
4 結 论
本文以南京浦仪长江公路大桥为工程背景,通过气弹模型试验研究了自立状态下钢桥塔全钢独柱桥塔-塔吊联合体系以及自立状态桥塔体系的抖振响应,主要研究结论如下:
1)桥塔顶部、塔吊顶部与塔吊悬臂端位移响应均值可近似表示为风速的二次函数;而位移响应均方差则随风速的变大呈现出波动性增加的规律.
2)对比联合体系模型试验与自立状态桥塔体系试验结果可以发现,塔吊对风场的扰动作用会显著减小桥塔顶部顺风向位移响应均值与桥塔顶部位移响应均方差.
3)联合体系模型试验结果表明,设计基准风速下,桥塔顶部与塔吊悬臂端位移响应均值随风偏角的变化呈现出相似的规律,且其极值多在斜风下得到.
4)联合体系模型试验结果表明,设计基准风速下,桥塔顶部与塔吊悬臂端位移响应均方差随风偏角的变化也呈现出相似的规律,极值多在斜风下得到.
5)比较塔吊与桥塔的抖振响应均方差表明,横桥向塔吊响应小于钢桥塔,而顺桥向塔吊响应则由于高阶振型的局部振动贡献存在明显的振动放大现象.
参考文献
[1] 朱梦雅,陆崟栋. 泰州大桥钢塔阻尼测试和分析[J]. 公路交通科技(应用技术版),2014,10(12):222—226.
ZHU M Y,LU Y D. Damping ratio test and analysis of steel pylon of Taizhou Bridge[J]. Journal of Highway and Transportation Research and Development(Application Technology Edition),2014,10(12):222—226. (In Chinese)
[2] 王中文,朱宏平,廖海黎,等. 钢桥塔裸塔状态涡激振动的TLD减振方法研究[J]. 华中科技大学学报(城市科学版),2009,26(2):9—11.
WANG Z W,ZHU H P,LIAO H L,et al. Vortex-induced vibration reduction of steel free-stangding tower using tuned liquid damper [J]. Journal of Huazhong University of Science and Technology (Urban Science Edition),2009,26(2):9—11. (In Chinese)
[3] 马婷婷,葛耀君,赵林. 大跨度斜拉桥施工阶段抗风性能变化规律[J]. 振动与冲击,2013,32(12):100—104.
MA T T,GE Y J,ZHAO L. Wind-resistant behavior of a long span cable-stayed bridge during construction[J]. Journal of Vibration and Shock,2013,32(12):100—104. (In Chinese)
[4] 张志田,吴肖波,葛耀君,等. 悬索桥吊杆风致内共振及减振措施初探[J]. 湖南大学学报(自然科学版),2016,43(1):11—19.
ZHANG Z T,WU X B,GE Y J,et al. Wind induced internal resonance and the control method of suspension bridge hangers[J]. Journal of Hunan University(Natural Sciences),2016,43(1):11—19. (In Chinese)
[5] 陶天友,王春峰,王浩,等. 超大跨度斜拉橋裸塔风致抖振MTMD控制研究[J]. 空气动力学学报,2015,33(5):678—685.
TAO T Y,WANG C F,WANG H,et al,Buffeting control of the free-standing tower of a super-long-span cable-stayed bridge using MTMD[J]. Acta Aerodynamica Sinica,2015,33(5):678—685. (In Chinese)
[6] 孙长亮. 山区大跨斜拉桥桥塔抖振响应研究[D]. 成都:西南交通大学,2013:1—8.
SUN C L . Buffeting analysis for long-span cable-stayed bridge tower in mountain area [D]. Chengdu:Southwest Jiaotong University,2013:1—8. (In Chinese)
[7] 王统宁,马麟,刘健新,等. 基于混合编程的大跨桥梁桥塔抖振时域分析[J]. 长安大学学报(自然科学版),2009,29(3):68—72.
WANG T N,MA L,LIU J X,et al. Time-domain buffeting analysis of the tower of long-span bridges on the basis of mixed programming[J]. Journal of Changan University (Natural Science Edition),2009,29(3):68—72. (In Chinese)
[8] 周奇,朱乐东,郭震山. 斜风下典型桥塔抖振性能的比较[J]. 东南大学学报(自然科学版),2009,39(S2):126—132.
ZHOU Q,ZHU L D,GUO Z S. Comparison on buffeting performance of typical pylons under skew wind[J]. Journal of Southeast University (Natural Science Edition),2009,39(S2):126—132. (In Chinese)
[9] 胡庆安,乔云强,刘健新,等. 斜风作用下桥塔施工阶段抖振性能[J]. 交通运输工程学报,2008,8(2):40—43.
HU Q A,QIAO Y Q,LIU J X,et al. Buffeting performance of bridge tower under yawed wind during construction [J]. Journal of Traffic and Transportation Engineering,2008,8(2):40—43. (In Chinese)
[10] 车鑫,李加武,高斐,等. 斜风作用下桥塔自立状态下风洞试验及抖振性能分析[J]. 公路交通科技,2012,29(10):84—87.
CHE X,LI J W,GAO F,et al. Wind tunnel test and analysis of buffeting performance of free-standing pylon of cable-stayed bridge under skew wind [J]. Journal of Highway and Transportation Research and Development,2012,29(10):84—87. (In Chinese)
[11] 胡航. 大跨度斜拉桥施工阶段抗风及控制措施研究[D]. 成都:西南交通大学,2014:8—28.
HU H. Mitigation for wind-induced vibration on long-span cable-stayed bridges in construction stage [D]. Chengdu:Southwest Jiaotong University,2014:8—28. (In Chinese)
[12] HERNNDEZ S,NIETO F,JURADO J . Aeroelastic studies of a cable stayed bridge in Talavera de la Reina,Spain[C]//Fluid Structure Interaction VII. Southampton:WIT Press,2013:39—50.
[13] LUO N,LIANG A X,LIAO H L,et al. Wind tunnel investigations for the Free Standing Tower of the Penang Second Bridge[J]. Applied Mechanics & Materials,2013,256/259:1577—1581.
[14] MA R J,HU X H. Aeroelastic model test study on a bridge pylon considering the interference effects of surrounding structures[J]. International Journal of Structural Stability and Dynamics,2013,13(5):1350011.
[15] 公路橋梁抗风设计规范:JTG/T 3360-01—2018 [S]. 北京:人民交通出版社股份有限公司,2018:15—24.
Wind-resistant design specification for highway bridges:JTG/T 3360-01—2018 [S]. Beijing:China Communications Press Co,Ltd,2018:15—24. (In Chinese)

