某型冰箱冷凝器的振动断裂分析

占双剑 王松青 陈滢 陈新涛 黄晓明

摘要：  针对某型冰箱冷凝器振动测试后冷凝管出现多处断裂破坏的问题，根据冷凝器所属的换热器类型提取设备及配套连接件的组合结构特征，建立可靠有效的有限元分析模型;利用有限元计算分析软件对部件进行结构模态分析，模拟扫频振动试验过程;根据有限元分析验证结构振动断裂结果，结合实际断裂部位特征与相连接冷却杆的结构变形，分析断裂发生的可能性;最后给出有效避免断裂的方法，用于优化振动测试方案。

关键词：  断裂; 扫频振动; 冷凝器; 模态分析; 有限元

中图分类号：  TB24;TB651文献标志码：  B

Analysis of vibration fracture on condenser of refrigerator

ZHAN Shuangjian1， WANG Songqing1， CHEN Ying1，

CHEN Xintao2， HUANG Xiaoming3

（1. Suzhou Advanced Integrated Mechanical Solutions Co.， Ltd.， Suzhou 215123， Jiangsu， China;

2. Zhangjiagang Core Electric Co.， Ltd.， Suzhou 215123， Jiangsu， China;

3. School of Energy and Power Engineering， Huazhong University of Science and Technology， Wuhan 430074， China）

Abstract： Aiming at the problems of multiple fracture of condenser tube of a refrigerator after vibration test， a reliable and effective finite element analysis model is established according to the characteristics of the combined structure of equipment and matching connectors of the condenser the type of heat exchanger extraction. Finite element analysis software is used to analyze the structural modal of the components and simulate the sweep vibration test process. The results of structural vibration fracture are verified by finite element analysis， and the possibility of fracture is analyzed based on the characteristics of the actual fracture position and the structural deformation of the connected cooling rod. Finally， an effective method to avoid fracture is given to optimize the vibration testing scheme.

Key words： fracture; sweep vibration; condenser; modal analysis; finite element

收稿日期： 2021-06-17修回日期： 2021-11-11

基金項目： 国家自然科学基金（51576077）

作者简介： 占双剑（1995—），男，江西上饶人，硕士，研究方向为力学，（E-mail）shuangjian_zhan1@163.com0引言随着人们生活水平的迅速提高，各种制冷设备在移动平台上得到越来越广泛的应用，如小型冰箱和车载空调。汽车在行驶过程中受到路面的激励作用，会发生持续不断的振动，这种振动会显著降低设备的使用寿命，故需要具有更好的抗振防抖性能以保证结构强度。在实际的工程生产中，一般常用试验测试校验产品的结构强度，但单次的试验测试无法准确判断试验过程中的结构损伤或破坏成因，需要重复多次试验。针对此类情形，利用有限元分析（finite element analysis，FEA）复现和验证样机试验特性，协助确定损伤或破坏成因，具备可行性与工程价值。近年来，振动领域内的科研和工程人员广泛应用FEA方法：朱兴高等[1]利用构建的有限元模型，校验多载荷情况下空间驱动机构的结构强度;仲崇明等[2]对冰箱往复式压缩机的振动进行有限元数值模拟，验证仿真手段用于振动响应分析的可行性;KUMAR等[3]利用有限元方法对变速器壳体进行振动分析，确认传动壳体的断裂原因;胡广文等[4]通过有限元建模分析，验证某型电机的性能指标。这些研究表明，FEA方法在振动分析领域具备较好的可实施性。其中，模态分析[5]在振动领域的工程应用中意义重要：可以评估现有结构的动态特性，获取设备的共振频率与相应振型以及对特定频率的激振响应;协助设计人员避开这些频率或弱化其带来的激励作用，避免过度振动，保证设备合理的使用寿命。孔祥强等[6]采用有限元法对冰箱局部制冷剂管道进行模态研究，确定最佳安装位置。

1预紧力作用下的模态方程一个完整的振动系统必须包含质量矩阵、刚度矩阵和阻尼矩阵[7]。其中，质量矩阵储存系统的动能，刚度矩阵储存系统的势能，阻尼矩阵则代表能量在不同系统之间的转换。系统振动后的形态就是模态，这是一个基于物理涵义的描述，对应到数学上就是非齐次微分方程的特征值问题。结构振动的基本动力学方程为[8]：Mx··+Cx·+Kx=F    （1）式中：M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;F为激振力列向量;x··为加速度响应;x·为速度响应;x为位移响应。假定系统为自由振动并忽略阻尼，则Mx··+Kx=0    （2）假定系统为简谐振动，即x=Xsin（ωt），则（K-ω2M）x=0    （3）上述方程的特征值ωi（i的范围是从1到自由度的数目）也是对应情况下结构的自然振动圆频率（rad/s）。有限元计算中，输出基本为自然频率fi（也称固有频率）。特征向量xi表示振型，即假定系统以频率fi振动时的形状，fi=ωi/（2π）    （4）在螺栓预紧过程中，连接结构内部会产生一定的预应力，导致结构整体刚度K产生一定的刚度扰动ΔK，因此预紧力作用下的螺栓连接结构模态方程[9]为Mx··+（K+ΔK）x=0    （5）此时，ΔK引起固有频率产生一定扰动，螺栓预紧力引起相同振型的固有频率平方的偏移[10-11]，其相对偏离大小与结构刚度K，预紧力引起的刚度矩阵改变量ΔK及质量矩阵有关。

2冷凝器的结构很多工程振动问题较为复杂，系统的模态求解主要采用FEA软件和工程建模相结合的方式，本文使用HyperMesh与Abaqus，对目标冷凝器的振动模态进行联合仿真研究。针对某型冷凝器在扫频振动试验测试过程中出现的冷凝管开裂和断裂现象，建立相应的有限元计算模型，编译计算子程序，展开模态分析，确定现有结构的共振频率，模拟冷凝器在振动台架扫频试验条件下的全程反应，结合疲劳寿命分析手段，查找導致局部冷凝管管壁破坏的原因。本文研究的目标型冷凝器为传统的丝管式冷凝器[12]，其具备体积小、质量轻、散热效果好、易批量生产等优点，在小型制冷领域的应用极为广泛。丝管式冷凝器的结构主要是将邦迪管弯成多个S形，与多根钢丝点焊在一起。当冷凝管内部的高温制冷剂流过时，通过与钢丝的热传导和外部的冷却风进行散热，制冷剂由过热态转为过冷态或饱和液态[13]。该型冷凝器的冷凝管与钢丝根据GB/T 23134—2008[14]的标准要求进行焊接。需要注意，该标准对于焊接融合深度没有明确要求。为保证后续仿真的真实性，剖开原件进行观察，测得钢丝焊接处管路内壁的突起高度约为0.25 mm，确认管壁基本未变薄，见图1。

冷凝器所有部件的材料皆为钢材，其中：冷凝管的材料为182MT50镀铜钢管（邦迪管），平均密度6.8 g/cm3，屈服强度约278 MPa;钢丝的材料标号为195F，平均密度7.85 g/cm3，屈服强度约195 MPa。

3FEA计算

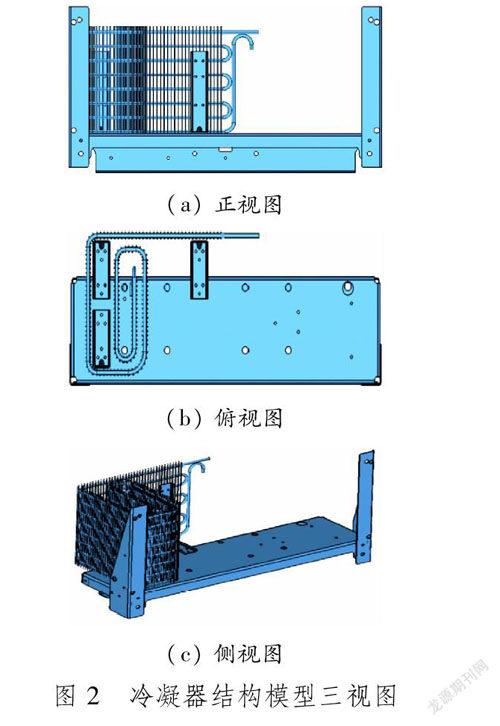
3.1有限元模型的建立该型冷凝器的结构模型见图2，其本体基本上由重复的杆管结构组成，依靠悬臂梁与底板连接。

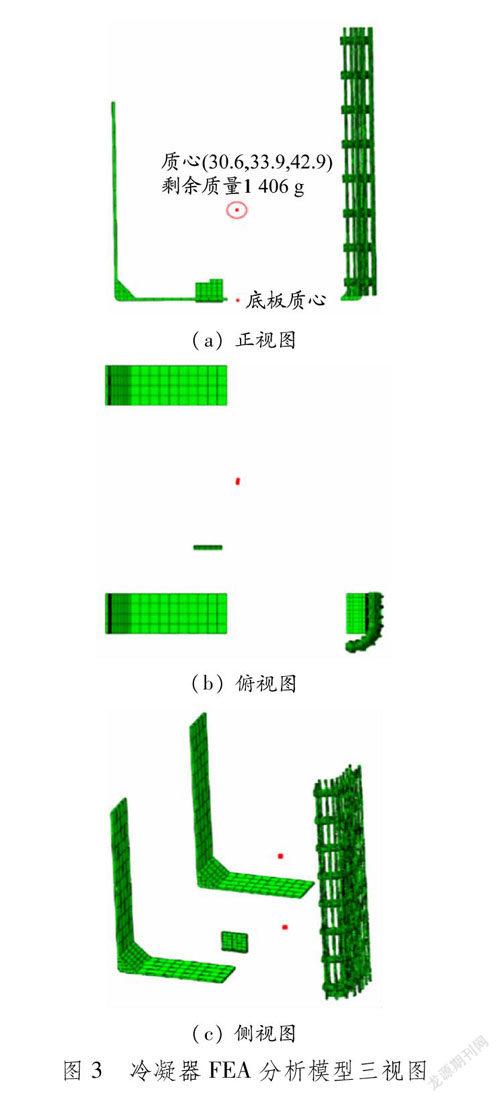
鉴于该冷凝器的破坏部位均是冷凝管和钢丝的焊接部位，且都位于冷凝器的一个侧面，位置比较集中，如果直接进行全尺寸结构化网格建模，会出现非常大的有限元模型，计算压力较大。为提高分析效率，在保证整体结构质量正确分布和支持部位结构合理的前提下，建立优化的FEA模型（见图3），可以准确追踪结构破坏出现的支持面的应力应变状况。剩余部分（包括管道、散热棒和散热风扇的3种结构）以质点载荷的形式给出，共计1 406 g。整个FEA模型网格全部采用结构化六面体单元，单元质量完全满足工程分析精度需求，FEA模型整体的自由度超过300万。

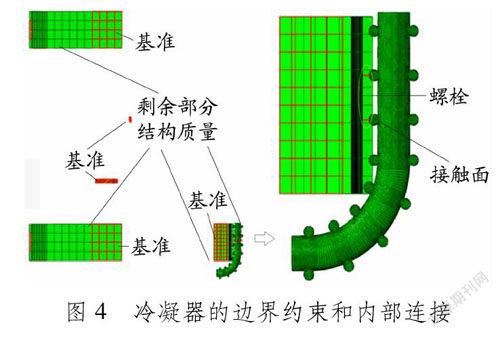
3.2载荷与约束的施加本文采用的边界约束条件和内部组装关系见图4。先通过3个支撑架以及分析段的界面，保持对冷凝管和钢丝质量点的支撑与连接关系，再通过4个支撑架与底板的连接构成整体模型。

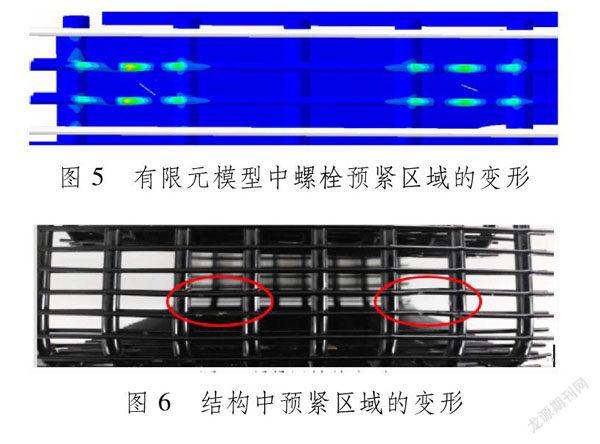
在静应力分析中，完全约束底板的位移自由度，再对全局施加沿z方向的重力载荷。同时，在分析段模拟螺栓连接及其预紧力，螺栓的预紧力可根据其公称直径以及强度，对照螺栓预紧力参照表查询得到。本文结构采用M4螺栓且强度为8.8级，螺栓的预紧力取3 825 N。此外，以单向弹簧模拟支撑架和散热棒外壁的接触关系。在后续模拟扫频振动的受迫简谐振动分析中，逐步按照振动条件放开底板在振动方向上的自由度约束，并根据实际试验的载荷条件加载频率和振幅/加速度。确认加载和边界条件的定义后，在重力和底座组装状态下模拟螺栓预紧力所导致的材料变形程度[15]（见图5和6），发现螺栓预紧部位发生一定程度的塑性应变，与实际结构相符。同时，也可以判断重力载荷对结构几乎不产生影响。

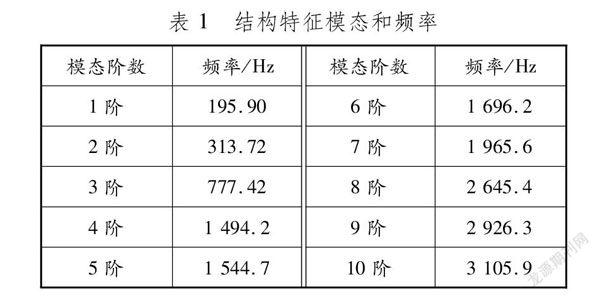
3.3预紧力作用下的模态分析模拟系统在简谐激励下的运动状态，并按照线性扰动分析方法进行谐振计算，获取系统的模态特征。在预紧状态下系统前10阶模态对应频率计算结果见表1。

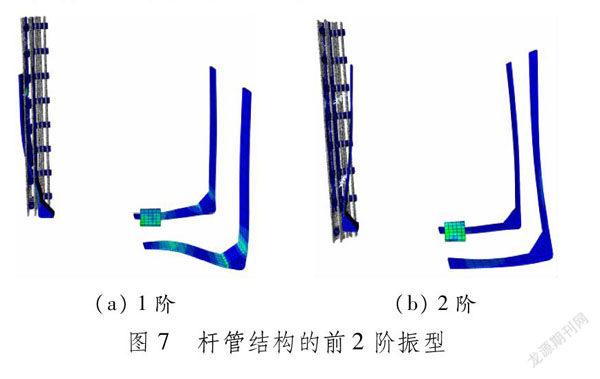
此外，分析结构的前2阶振型（见图7），因钢板在x轴往复摆动，不断冲击着冷凝管，表现为螺栓连接区域容易失效变形甚至断裂。

在该冷凝器的设备振动测试试验中，x、y、z这3个方向上分别进行8 h的振动，并以扫频形式进行测试。z轴方向的振动参数[16]为：当振动频率为10～25 Hz时，振幅为1.2 mm;当振动频率为25～500 Hz时，加速度为30 m/s2。在x和y方向测试时，振幅和加速度均减半。对比实测结果与模态分析结论可知：当前试验设置的扫频范围完全包括前2阶的模态频率，满足结构振动测试的要求;确认扫频振动试验合理，排除试验条件设置不当导致结构振动断裂的可能性。

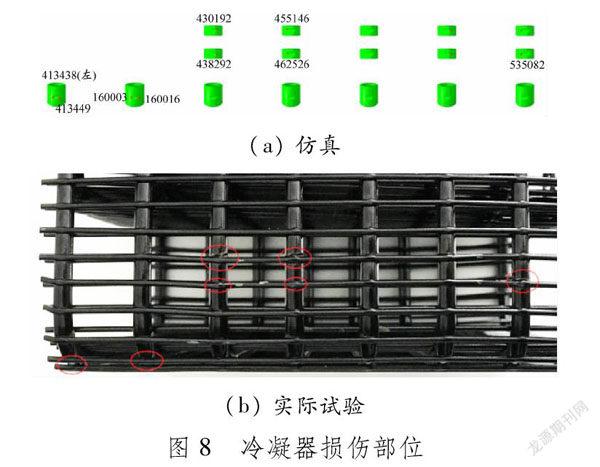
3.4模拟扫频振动试验模拟扫频振动试验，分析断裂破坏的可能原因，其目的是计算出结构在激振力频率下的响应，并得到系统的动力响应与系统振动频率的关系曲线，也称幅频曲线[17-18]。在有限元定义时，放开底板在振动方向上的自由度约束，并在3个方向对系统进行简谐激励加载，模拟振动源，具体幅值参照振动试验条件的定义。根据结构组合关系和单元特征，设置全局阻尼系数。在10～500 Hz区间全程计算系统反应。通过比对实际试验断裂部位与模型计算结果（见图8），确定有限元模型对应断裂部位的节点（结构主要失效部位位于螺栓连接区域），并提取节点位置处的振动幅值。

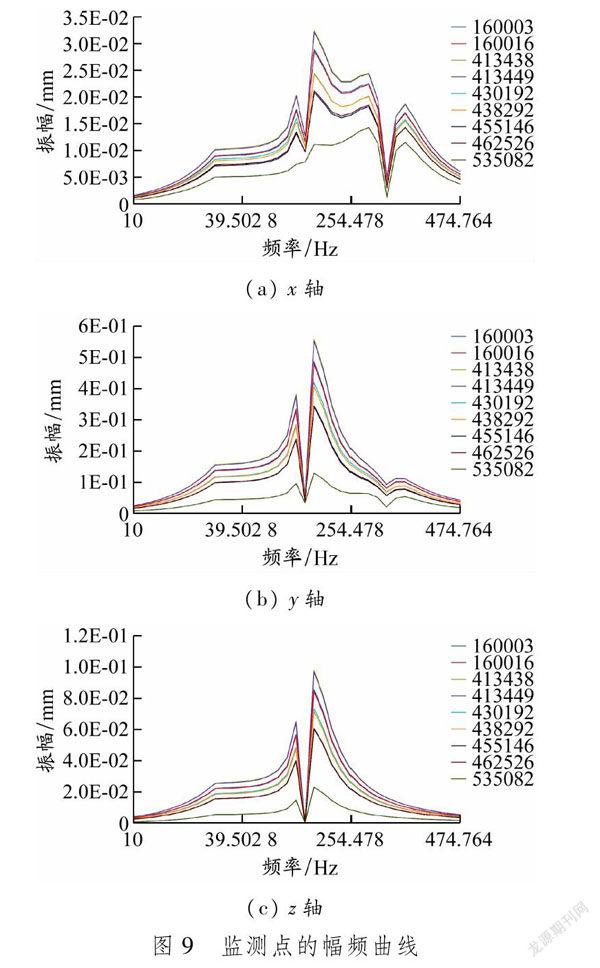
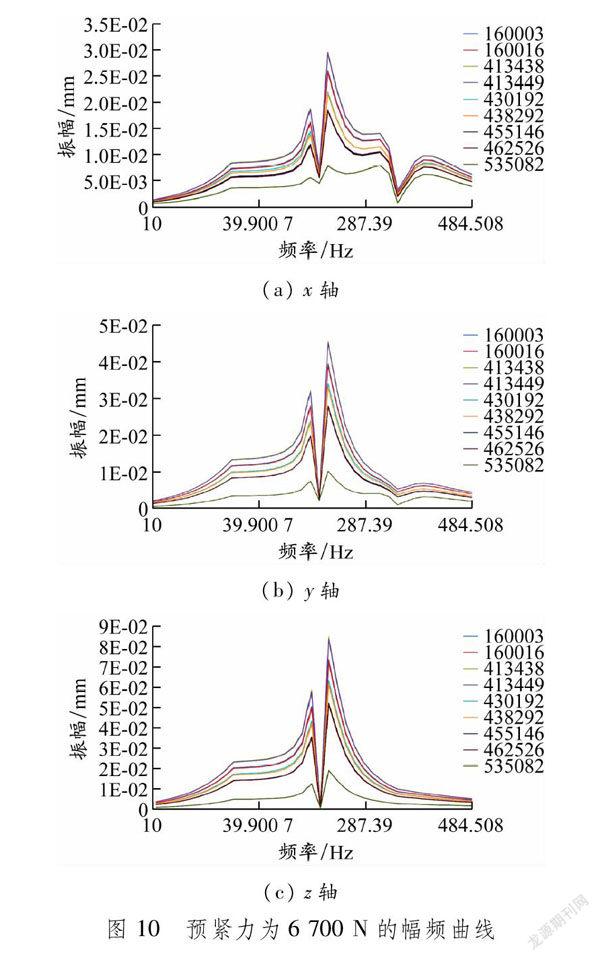
在x、y、z这3个方向上，振幅随激发载荷频率的变化关系见图9，图中的代号值为其网格模型上对应的节点数。综合上述信息可知，在10～500 Hz的激振频率区间内，监测点的响应值达到控制点的2倍以上，出现较大的突变振幅，可判断该响应值对应的频率为共振点，即产生共振。距离激振点越近的节点，产生共振的可能性越大。为进一步探讨结构的振动响应问题，对螺栓强度进行加强，即增加预紧力，观察其对振动测试是否有影响。图10是预紧力为6 700 N的幅频曲线。

对比图9和10可知，结构监测点的响应值整体向右偏移，可见预紧力的增加可以提高结构的固有频率。这表明：在扫频范围内的振动激励条件下，提高预紧力可以在一定程度上有效避免出现共振点。

4结论（1） 通过有限元仿真方法进行部件的振动模态分析，同时模拟扫频振动试验，发现该部件在振动试验环境下会发生共振现象，结构内部会产生较大的振动应力，在长时间激励载荷冲击下容易发生疲劳

断裂。仿真结果表明，增大螺栓预紧力可有效提高结构刚度，避免发生振动断裂。

（2） 从工艺加工角度看，另一个导致冷凝管断裂的原因是冷凝管与冷却杆焊接后，未对部件上留有的残余应力进行处理[19-20]（绝大多数部件测试时会忽略）。局部残余应力在振动条件下形成的应力集中，有很大的可能性会导致破坏现象的发生。参考文献：

[1]朱兴高， 栾家辉， 代永德. 基于有限元的太阳翼驱动机构结构强度分析验证[J]. 计算机辅助工程， 2019， 28（2）： 11-14. DOI： 10.13340/j.cae.2019.02.003.

[2]仲崇明， 万泉， 蒋伟康. 往复式压缩机振动的有限元数值分析与实验研究[J]. 振动与冲击， 2011， 30（5）： 156-160. DOI： 10.3969/j.issn.1000-3835.2011.05.032.

[3]KUMAR A， JAISWAL H， PANDEY A， et al. Free vibration analysis of truck transmission housing based on FEA [J]. Procedia Materials Science， 2014， 6： 1588-1592. DOI： 10.1016/j.mspro.2014.07.141.

[4]胡文广， 韩业鹏， 邸建忠， 等. 基于有限元的交流伺服电机仿真分析[J]. 计算机辅助工程， 2020， 29（1）： 71-74. DOI： 10.13340/j.cae.2020.01.014.

[5]李星占， 岳晓斌， 黄文， 等. 振动响应传递率及其工作模态分析方法综述[J]. 振动与冲击， 2019， 38（18）： 24-34. DOI： 10.13465/j.cnki.jvs.2019.18.004.

[6]孔祥强， 陈丽娟， 李瑛. 制冷剂管道参数对冰箱振动影响特性[J]. 振动与冲击， 2015， 34（20）： 209-213. DOI： 10.13465/j.cnki.jvs.2015.20.035.

[7]商霖. 基于Ansys有限元分析的模态质量计算方法[J]. 导弹与航天运载技术， 2011（3）： 55-57. DOI： 10.3969/j.issn.1004-7182.2011.03.012.

[8]R·克拉夫， J·彭津. 结构动力学[M]. 王光远， 等. 译. 2版. 北京： 高等教育出版社， 2019.

[9]CRAVEUR J. Modélisation par éléments finis[M]. 3rd ed. Paris： Dunod， 2008.

[10]邵俊， 伍济钢， 周根， 等. 预紧力对螺栓联接机匣模态频率的影响研究[J]. 噪声与振动控制， 2019， 39（6）： 61-65. DOI： 10.3969/j.issn.1006-1355.2019.06.011.

[11]傅志方， 华宏星. 模态分析理论与应用[M]. 上海： 上海交通大学出版社， 2000.

[12]成耀龙， 徐明仿， 吴业正. 丝管式冷凝器周围空气温度分布的实验研究及仿真[J]. 制冷学报， 2006， 27（2）： 6-9. DOI： 10.3969/j.issn.0253-4339.2006.02.002.

[13]TANDA G， TAGLIAFICO L. Free convection heat transfer from wire-and-tube heat exchangers[J]. Journal of Heat Transfer， 1997， 119（2）： 370-370. DOI：10.1115/1.2824235.

[14]家用电冰箱冷凝器： GB/T 23134—2008[S].

[15]闫琳， 任娜， 康建伟， 等. 浅析预紧力对螺栓强度的影响[J]. 汽車实用技术， 2018（17）： 98-99. DOI： 10.16638/j.cnki.1671-7988.2018.17.031.

[16]车载冰箱： T/GDBX 005—2018[S].

[17]叶鲁浩， 王志， 张进生， 等. 基于Ansys圆锯片模态分析及谐响应分析[J]. 金刚石与磨料磨具工程， 2015， 35（4）： 41-46. DOI： 10.13394/j.cnki.jgszz.2015.4.0009.

[18]CRAVEUR J， JETTEUR P. Introduction à la mécanique non linéaire[M]. Paris： Dunod， 2010.

[19]夏承钰， 朱广宇， 赵建祖， 等. 焊接冷凝管在役断裂原因分析[J]. 热力发电， 2006（12）： 67-69. DOI： 10.19666/j.rlfd.2006.12.022.

[20]HAN X M， TAN J Z， WANG R Q， et al. A study on welding residual stress in elliptical tube to tube sheet joint of a phthalic anhydride switch condenser[J]. Procedia Engineering， 2015， 130： 544-551. DOI： 10.1016/j.proeng.2015.12.262.（编辑陈锋杰）