钝体稳定火焰尾流特性的数值模拟研究*
李钰航,李文龙,吴宝元
(1.液体火箭发动机技术重点实验室,西安航天动力研究所,西安 710100;2.航天推进技术研究院,西安 710100)
0 引言
冲压发动机一般工作在飞行马赫数大于2的条件下,来流空气经过进气道压缩之后,速度仍然很高,远大于燃料的火焰传播速度。因此,冲压发动机燃烧室需要采用特殊的火焰稳定结构,保证燃料在燃烧室内有足够的停留时间,使得雾化、掺混、燃烧等复杂过程得以稳定地进行[1-2]。
钝体稳焰器具有结构简单、工作可靠等优势,在工程中得到了广泛应用[3]。其原理是利用钝体后方的气流低速区驻定火焰,并以此作为点火源点燃剩余燃料,从而在高速气流中实现稳定燃烧。然而,在实际工程研制过程中,由于设计的不合理,常会出现火焰吹脱、稳焰器烧蚀以及燃烧不稳定等问题。为了解决这些问题,有必要对稳焰器尾流的流动与燃烧过程进行深入研究[4]。钝体稳焰器尾流的流动结构较复杂,其中低速回流区与高速主流之间存在剪切层,具有流动本质不稳定特性[5-6]。早期的实验研究观察到振荡燃烧时,稳焰器尾流涡结构与稳定燃烧时存在明显区别,并提出了将非定常涡脱落作为燃烧不稳定的重要诱因[7-8]。随后,针对钝体预混燃烧的一些研究,又对比了冷态与热态[9-10]、不同钝体形状[11]等条件下流动的差异,指出化学反应放热能够改变尾流涡结构。近期对于钝体尾缘喷注燃料的非预混火焰的研究[12-13]又表明,反应区与剪切层的相对位置对于尾流结构具有显著影响,燃料和反应放热区的分布是火焰动力学的决定因素。
由于实验研究周期长、费用高且获得的数据有限,计算流体力学方法已成为钝体稳焰器研究的重要手段。已有的研究表明,传统的雷诺平均湍流模拟(RANS)方法在流动分离区域严重高估了涡粘性;大涡模拟方法(LES)则对壁面附近网格尺寸的要求很高[14];分离涡方法(DES)能够在对近壁区流动模化的同时,准确处理流动分离区的涡粘性,适合于对钝体稳焰器的数值模拟[15]。湍流燃烧方面,基于火焰面概念的燃烧模型能够在考虑详细化学反应机理的同时,通过预先建表过程减小计算量,适用于预混燃烧、非预混燃烧及部分预混燃烧的模拟。
本文以Volvo钝体稳定火焰的试验构型为对象进行数值模拟,采用改进延迟分离涡模型(IDDES)与火焰面生成流形方法(FGM)处理湍流流动与化学反应,研究钝体稳焰器的冷态与热态流动特性,分析燃烧放热对时均流场及钝体尾流中非定常涡结构的影响。
1 数学物理模型
1.1 流动控制方程
针对湍流预混燃烧问题,本文采用的控制方程包含连续性方程、动量方程、混合分数以及进度变量输运方程:
(1)
(2)
(3)
(4)
上式均经过滤波操作。其中,DZ与DC分别为混合分数及进度变量的扩散系数;Dt为相应的湍流扩散系数;ωC为进度变量源项;τij为亚格子应力项,其表达式为
(5)
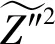
(6)
式中Δ为滤波尺度;CZ为常量系数,CZ=0.07。
1.2 湍流模型
为了对钝体后方的大范围分离流动进行准确的建模,同时兼顾计算量,本文选取基于k-ωSST的改进延迟分离涡湍流模型:
(7)
-ρβω2-ρ(F1-1)CDkω+Sω
(8)
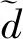
(9)
其余参数可参考文献[16]。
1.3 燃烧模型
本文研究钝体稳焰器的预混火焰,为了考虑详细化学反应机理,采用火焰面生成流形方法(FGM)处理湍流预混燃烧。该方法在进度变量空间上求解一维预混层流火焰面方程:
(10)
(11)
其中,χC为进度变量C的标量耗散率,定义为
(12)
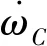
(13)
式中A为反应速率常数;ρu为未燃混合气密度;St为湍流火焰速度,定义可参考文献[17]。
湍流化学交互作用(TCI)通过概率密度函数方法处理。
1.4 计算域及网格划分
针对Volvo钝体冷流与燃烧试验[18]进行数值模拟研究,计算域及其边界条件设置如图1所示。丙烷燃料在钝体上游喷入并与空气充分混合,保证气流经过钝体时为完全预混状态。从钝体上游0.32 m开始选取1.0 m长度的长方体计算域,其横截面为0.12 m ×0.10 m的矩形。钝体为宽度0.04 m的实心正三棱锥。流场域上下实体面为绝热无滑移壁面,左右两侧采用周期性边界条件以模拟展向无限长的结构。入口条件给定流量,出口采用压力出口边界。采用SIMPLE算法进行非定常计算,时间步内迭代至残差小于10-4时,认为当前时间步收敛,计算时间步长为2×10-6s,时均统计时间为1 s。
设置三种计算工况,分别对应于冷态流动以及两种不同当量比的预混火焰,具体如表1所示。
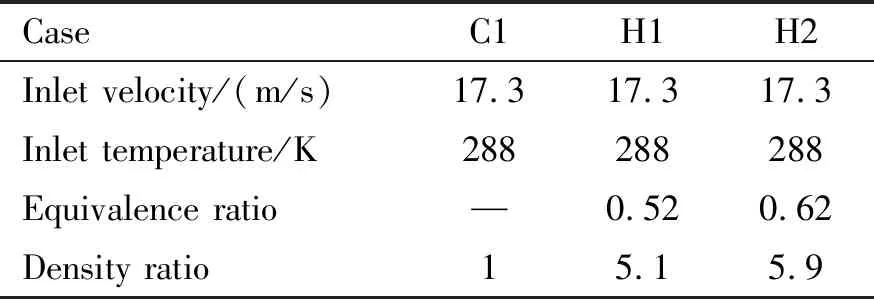
表1 算例工况设置
对计算域的网格划分采用全局六面体网格,具体如图2所示,网格总量约为1 600 000。为保证计算的准确性,对壁面附近以及钝体尾缘剪切层位置进行网格加密,所有壁面法向第一层网格特征尺寸y+<10。
2 计算结果及分析
2.1 数值模拟结果与实验数据的校验
为了验证本文计算结果的正确性,将冷态与热态流动模拟结果中多个位置的轴向速度及温度分布与实验测量数据进行了对比。
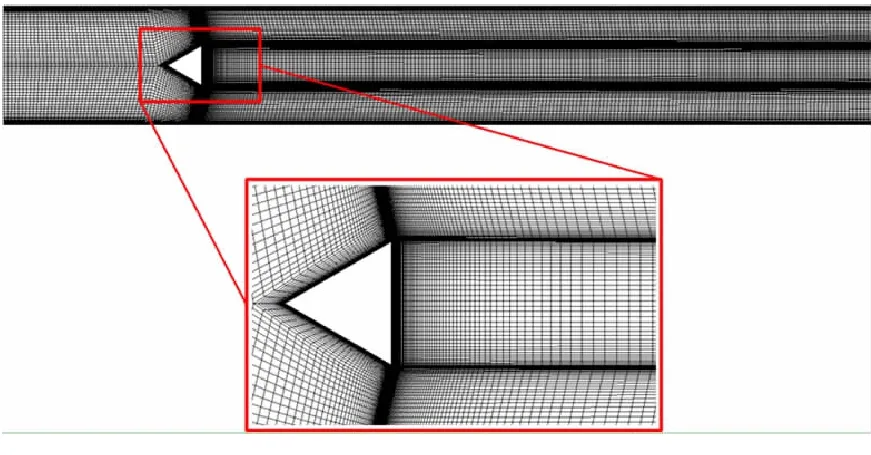
图2 Volvo算例的网格划分
图3展示了冷态流场中心轴线上轴向时均速度与实验的对比结果,数值计算分别采用了IDDES方法与k-ωSST模型的非定常雷诺平均(URANS)方法。结果显示,IDDES与实验吻合良好,能够准确预测流动分离区的速度分布。URANS则大幅高估了分离区的回流速度以及分离区下游的主流速度。其主要原因是钝体尾流剪切层中大尺度脉动的各向异性特征较强,而URANS方法基于线性涡粘假设,无法解析大尺度涡向小尺度涡的能量级串过程。IDDES方法在自由流动区直接求解大尺度涡,在壁面附近对边界层进行模化,模拟此类存在局部分离的流动时具有很好的效果。

图3 流向平均速度分布与实验结果对比
图4给出了冷态工况C1与燃烧工况H2中三个不同轴向位置处的速度分布与实验测量值的对比结果,两工况计算结果均与实验结果吻合较好。由于工况H2存在燃烧放热,气体升温膨胀增加了主流速度,热物性变化使得剪切层位置的速度梯度更大。
图5给出了燃烧工况H2流场中两个轴向位置处温度分布与实验结果对比。对于x/D=0.95位置,计算结果对中心回流区温度计算准确,而对钝体尾缘后方温度梯度的预示过大。主要原因是钝体近场位置的火焰锋面由剪切层主导,湍流与燃烧的交互作用较强,概率密度函数方法对剪切层位置高温区域的横向扩散存在低估。随着流动向下游发展,剪切层不断增厚,温度径向变化趋势更加平缓。因此,x/D=9.4位置的计算结果更准确。
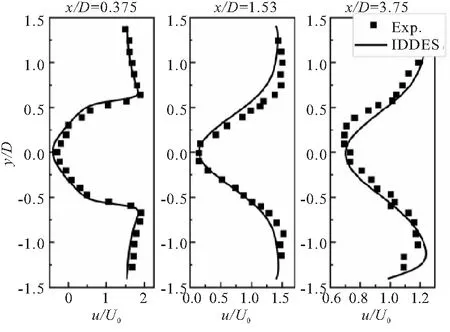
(a)Case C1
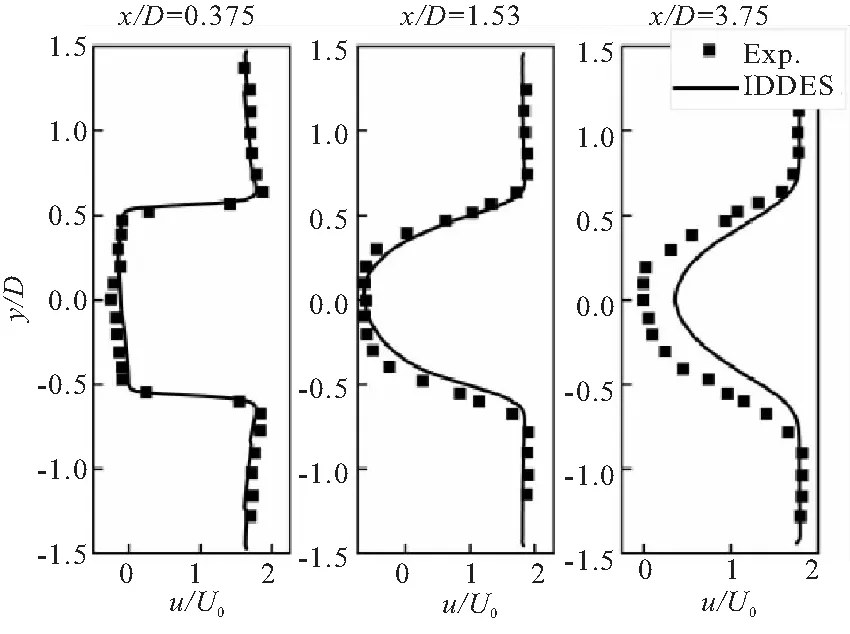
(b)Case H2

图5 不同位置的径向平均温度分布与实验结果对比
2.2 时均流场分析
图6给出了三种工况的时均轴向速度场。对于冷态工况,两侧的高速气流经过钝体之后,速度衰减较明显,速度在横向的分布很快趋于均匀,钝体后方所形成的回流区较短。对于燃烧工况,释热膨胀对气流的加速作用使得流道出口的速度更高,同时钝体两侧气流也不再减速。此外,燃烧工况中存在的气流膨胀并未使得回流区缩短,反而使其加长,这与火焰锋面两侧物性的剧烈变化及其对于剪切层所产生的影响相关。
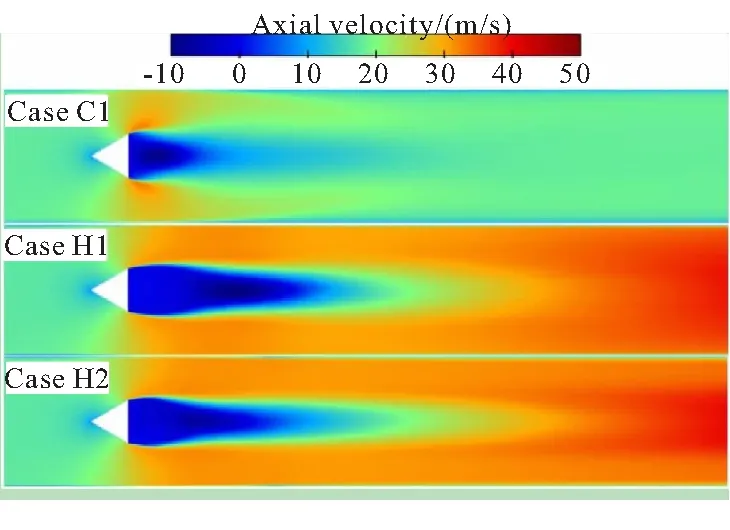
图6 三种工况的时均轴向速度场
图7给出了两个当量比不同的燃烧工况的平均温度分布。可见 ,对于低当量比工况H1,火焰最高温度约1530 K,高温产物集中于钝体后方的回流区内,在下游位置燃烧产物与两侧低温来流相互掺混,使得流场的平均温度降低至1200 K左右。对于当量比更高的工况H2,火焰最高温度约1700 K。由于高当量比可燃气的燃烧放热更为充分,高温区域一直延伸至下游。此外,H2工况时均温度场的剪切层厚度较薄,且几乎平行于来流方向。相比之下,H1工况时均温度场的剪切层更厚且呈现较大扩张角,这是由于火焰锋面在横向出现大幅度脉动导致的,与剪切层内的涡动力学特性相关,将在下文进一步讨论。
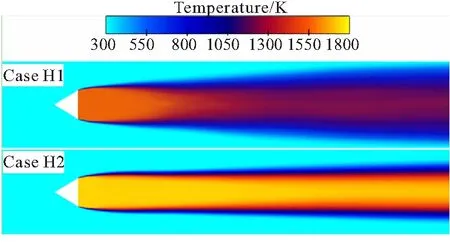
图7 燃烧工况的时均温度场
2.3 瞬态流场分析
2.3.1 流场涡结构分析
钝体尾流存在着复杂的涡结构,采用速度梯度张量第二不变量(Q-criterion)的等值面,可识别这些特征结构,进而分析钝体尾流的流动特性以及燃烧放热所产生的影响。
首先,对冷态流动进行分析。图8中的C1工况展现了两种典型的流动不稳定结构。其一是钝体两侧尾缘剪切层中的Kelvin-Helmholtz(K-H)不稳定性,这种不稳定的特征表现为高速主流与回流区交界面之间的二维小尺度涡。此小尺度涡作为界面上的初始扰动,在向下游发展的过程中不断放大,导致了交界面的翻转并产生了包含展向的三维结构。其二是钝体远场的Benard-Von Karman(BVK)不稳定性,这种不稳定的特征表现为尾迹区存在反对称分布的大尺度涡结构。值得一提的是,BVK不稳定是一种二次不稳定性,由一次不稳定发展而来[4]。剪切层中的涡结构在发展过程中放大,上下两侧的涡团在回流区截止位置发生融合,最终形成了BVK不稳定的涡结构。
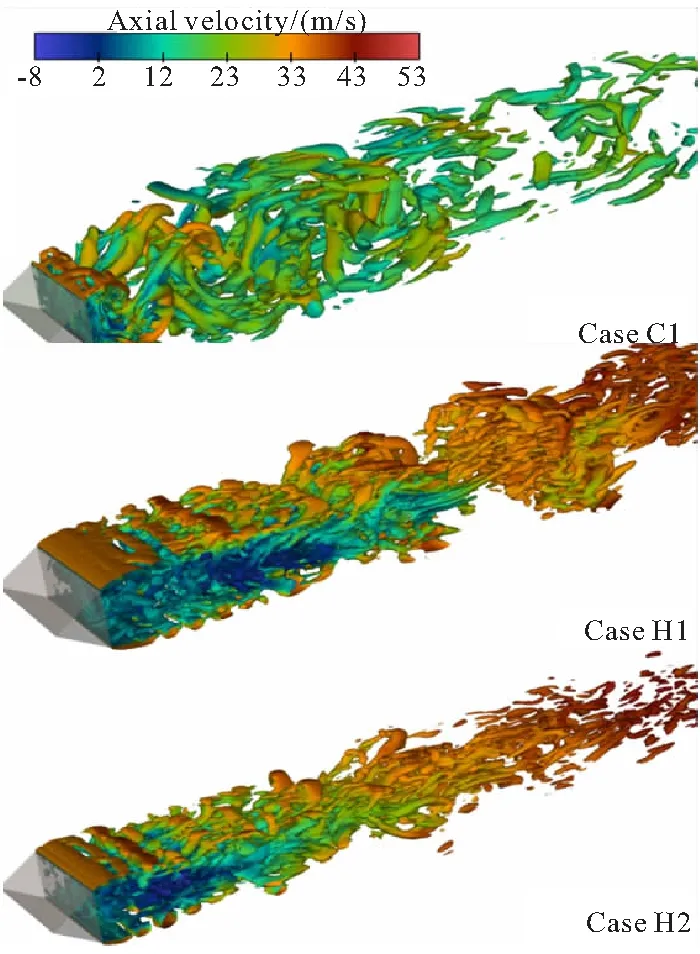
图8 速度梯度张量第二不变量等值面识别的涡结构
对于热态工况,火焰锋面位于钝体尾缘剪切层中,燃烧放热导致的气体膨胀和物性变化改变了剪切层的动力学特征。从宏观角度看,热态流场中最明显的变化是尾流中反对称结构的消失。由图8的H1工况可见,上下两侧剪切层中卷起两排并列的小尺度涡。这些涡结构的发展较为缓慢,不会迅速增长并形成反对称的BVK涡结构,而是以近似对称的形式间歇性地向下游对流。对于H2工况,由于当量比的增加,火焰温度上升,且气体膨胀比增加,涡量的间歇特征减弱。总体上看,燃烧放热抑制了BVK不稳定性,且当量比越大,抑制作用越强。
为了更深入解释火焰放热对剪切层的影响机理,借助如下的涡量输运方程[4,20]来进行分析:
(14)
上式右端各项表示不同作用对涡量的影响。第一项表示由涡结构的拉伸或收缩引起的涡量空间输运;第二项表示气体膨胀产生的影响;第三项为斜压作用生成项,由压力梯度与密度梯度不共线而引起;第四项为粘性引起的涡量生成。其中,斜压及气体膨胀项与粘性项符号相反,互成竞争作用。图9给出了x/D=1位置各涡量源项沿横向的分布。可见在剪切层位置,与冷流工况相比,热态工况中火焰锋面的释热作用引起了负的斜压涡量-(p×ρ)/ρ2和膨胀涡量-ω·u,其作用与粘性涡量生成项×[1/(ρ·τ)]相反,所以导致了钝体剪切流动涡量被抵消或削弱。这便解释了上述热态流场中剪切层涡卷起受到抑制以及BVK不稳定消失现象的成因。此外,高当量比工况H2的燃烧释热更剧烈。因此,其膨胀涡量相比H1工况更为明显,导致了前文所述对BVK不稳定性更强的抑制作用。

图9 涡量源项的横向分布
2.3.2 流动不稳定性的功率谱分析
对于上述的两种流动不稳定性,已有的一些研究给出了其相应频率的计算方法。其中,BVK不稳定性的特征频率为
(15)
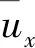
根据本文算例进行估算,相应频率约在 110~153 Hz范围内。对于K-H不稳定性,特征频率计算公式为
(16)
式中Srδ为采用当地边界层厚度定义的斯特劳哈尔数,其值对于湍流边界层约为0.044,边界层厚度δ的计算方法可参考文献[20]。根据本文算例设置进行估算,相应频率约在971.3 Hz附近。
为了分析钝体尾流中的流动不稳定性,在钝体尾缘(y=0.02 m)后方,设置多个测点,以监测局部位置的瞬时速度。图10给出了三种工况中钝体近场(x/D=1)及远场(x/D=4)位置的横向无量纲脉动速度v/U0的频谱分布。
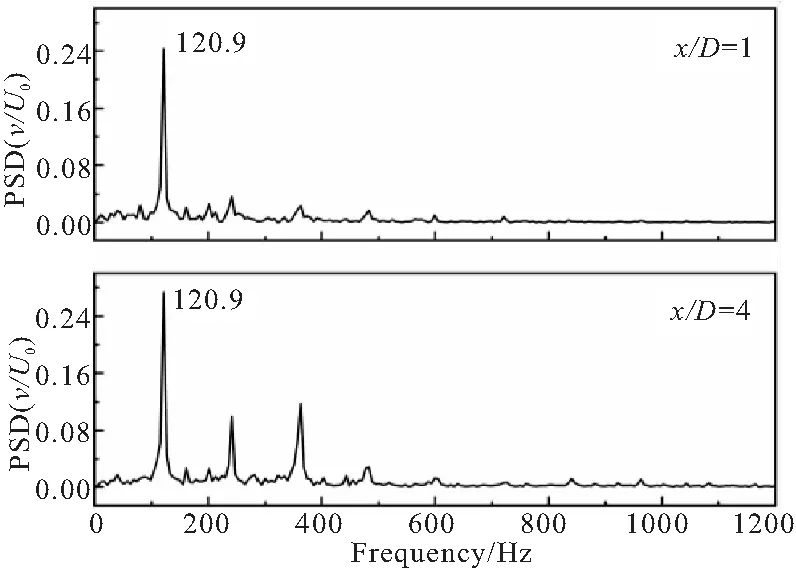
(a)Case C1
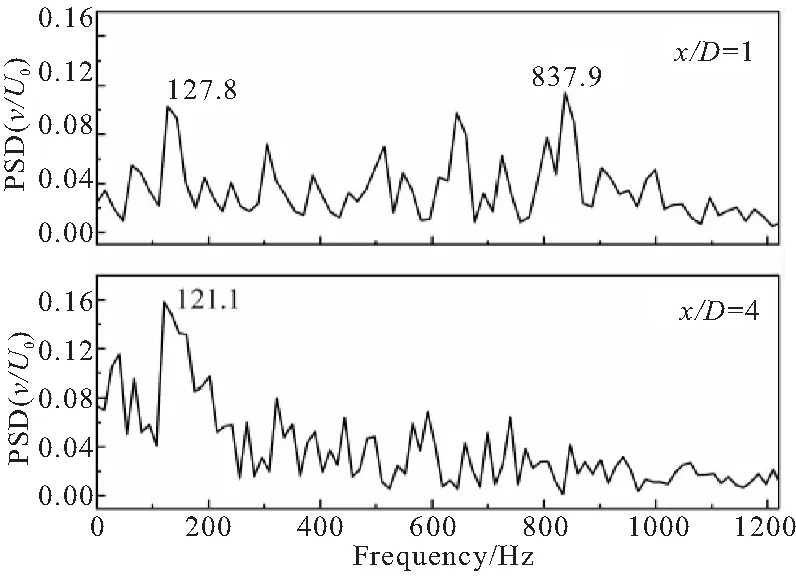
(b)Case H1

(c)Case H2
在冷态流动工况C1中,两个测点处的主导频率均为f=120.9 Hz,该频率对应于BVK不稳定。对于低当量比燃烧工况H1,近场测点主频837.9 Hz对应于K-H不稳定,但同时也存在127.8Hz的低频突峰;远场测点则仅剩下121.1 Hz的低频突峰。这说明H1工况中BVK不稳定虽受到一定程度的削弱,但并未完全消失,而是在更靠下游的位置起主导作用。对于高当量比燃烧工况H2,近场测点主频为952.7 Hz,与上文估算的K-H不稳定频率十分接近;远场测点主频降低为640.5 Hz。两测点均未见BVK不稳定对应的低频特征频率,表明其已被完全抑制。
3 结论
(1)采用IDDES湍流模型并结合FGM燃烧模型,能较准确地捕捉钝体稳焰器尾流的流动特征。
(2)钝体冷态尾流中存在BVK与K-H两种流动不稳定性。其中,BVK不稳定是由钝体两侧尾缘剪切层相互融合而发展成的二次不稳定。
(3)燃烧释热产生的体积膨胀与斜压效应能够抵消钝体尾缘剪切流动引起的涡量生成,从而抑制尾流中的BVK不稳定结构;来流中燃料当量比越高,抑制作用越明显。
(4)可以通过改变稳焰器几何结构或者燃料局部当量比来调节稳焰器后方尾流的涡动力学特性,进而消除由非定常涡脱落诱发的相应频率范围内的燃烧不稳定,改进燃烧室性能。

