基于移动平均及LSTM组合模型的火电厂日发电量预测研究
程鹏远,茅大钧,胡 涛
(上海电力大学 自动化工程学院,上海 200082)
0 引言
根据《中华人民共和国2020年国民经济和社会发展统计公报》所统计的信息,截止至2020年末,全国发电装机容量220 058万千瓦,其中火电装机容量124 517万千瓦,占比达56.58 %;全国发电量77 790.6亿千瓦时,其中火电53 302.5亿千瓦时,占比达68.52 %。火电目前以及在未来较长的时间里,依旧是我国电力的最主要来源。
当前火电厂主要是通过对比往年的发电量来对未来一定时间的发电量进行预测,没有建立相应科学模型〔1,2〕,预测结果存在一定误差,不利于发电及燃料采购计划的制定。目前相关预测研究多集中在电力需求侧用电总量和输配电侧的短期、超短期电力负荷精准预测,聚焦电力交易和电网基础安全〔3〕。但是,中长期发电量预测对电厂生产管理同样有重要意义,持续稳定且准确的发电量预测是发电企业现金流和利润率预测的关键〔4〕。
1 数据分析
火电发电计划由电网公司下达,发电计划制定受到经济增长、天气以及节假日等因素的影响〔5〕,本文结合上海市某火力发电企业2018年~2020年发电量历史数据,分析发电量变化的特性规律,建立相关的预测模型。
如图1所示,本文选取了2018年~2020年的日发电量数据,通过对历史发电量变化趋势的分析研究,不同年份日发电量变化趋势总体相对稳定,但在传统节日、异常天气及特殊时期发电量会产生明显变化,例如,2020年第一季度由于疫情因素,发电量出现了一个明显的持续时间较长的低谷。
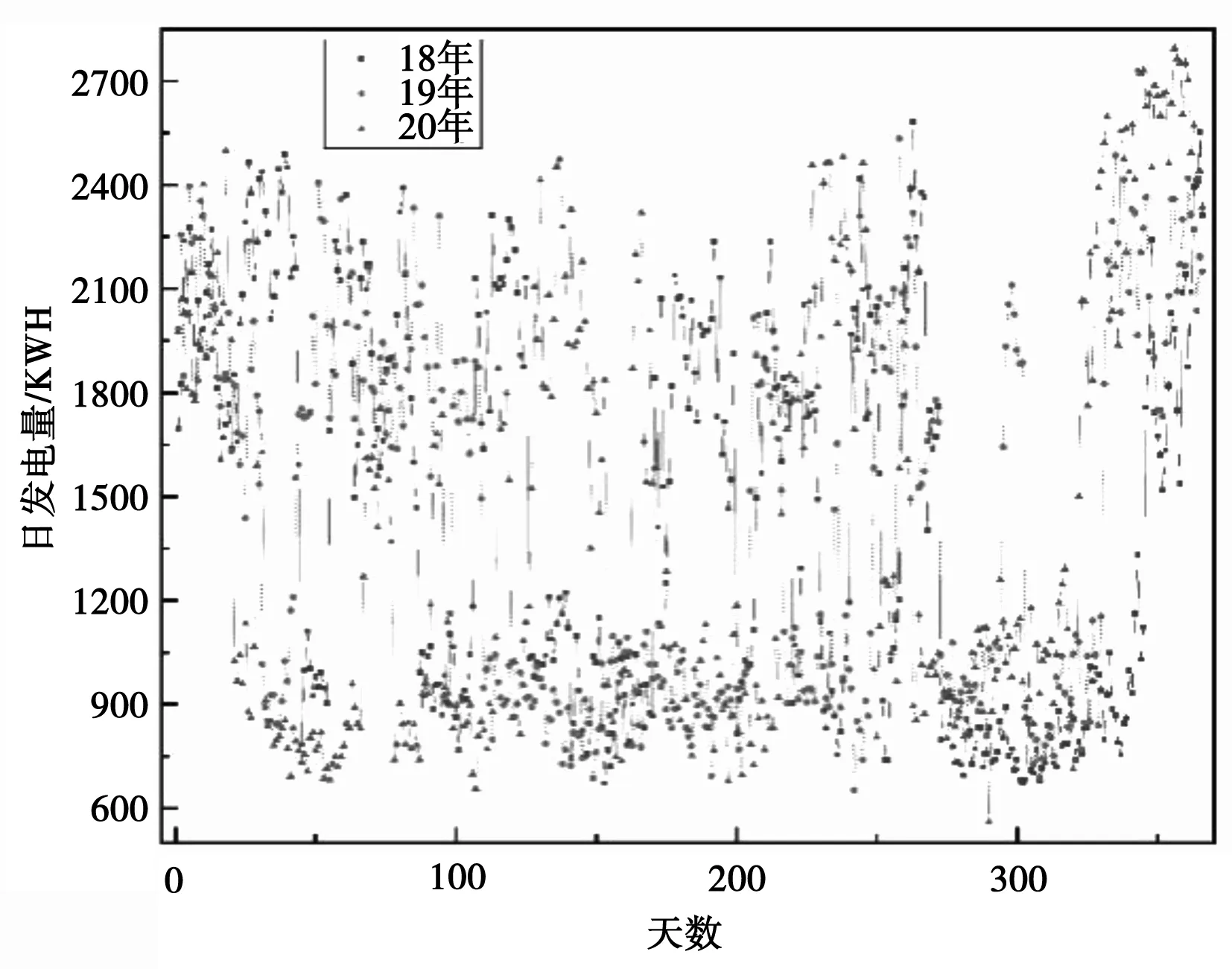
图1 发电量历史数据
在建模过程中若只考虑周期性,节假日和变化趋势,建模忽视大量历史数据中隐藏的非线性非周期性的特征,实际预测精度并不会提高。本文利用趋势移动平均法在预测时间序列数据中的优势,结合LSTM神经网络学习大量时序性历史数据中的隐藏关系的能力,组成新的火电企业日发电量预测模型。
2 移动平均法
移动平均法是在时间序列持续演变的过程中,按照顺序对含括若干数量的时序平均数进行运算,来对长期的变化趋势做出预测。在实际的时间序列数据中,经常会发生无规律波动,会对预测结果产生较大影响。移动平均法的运用可以减小和避免无规律波动的影响,从而保证对时间序列的长期变化趋势所做的预测具有准确性。移动平均法的种类有简单移动平均法,加权移动平均法和趋势移动平均法等。
2.1 简单移动平均法
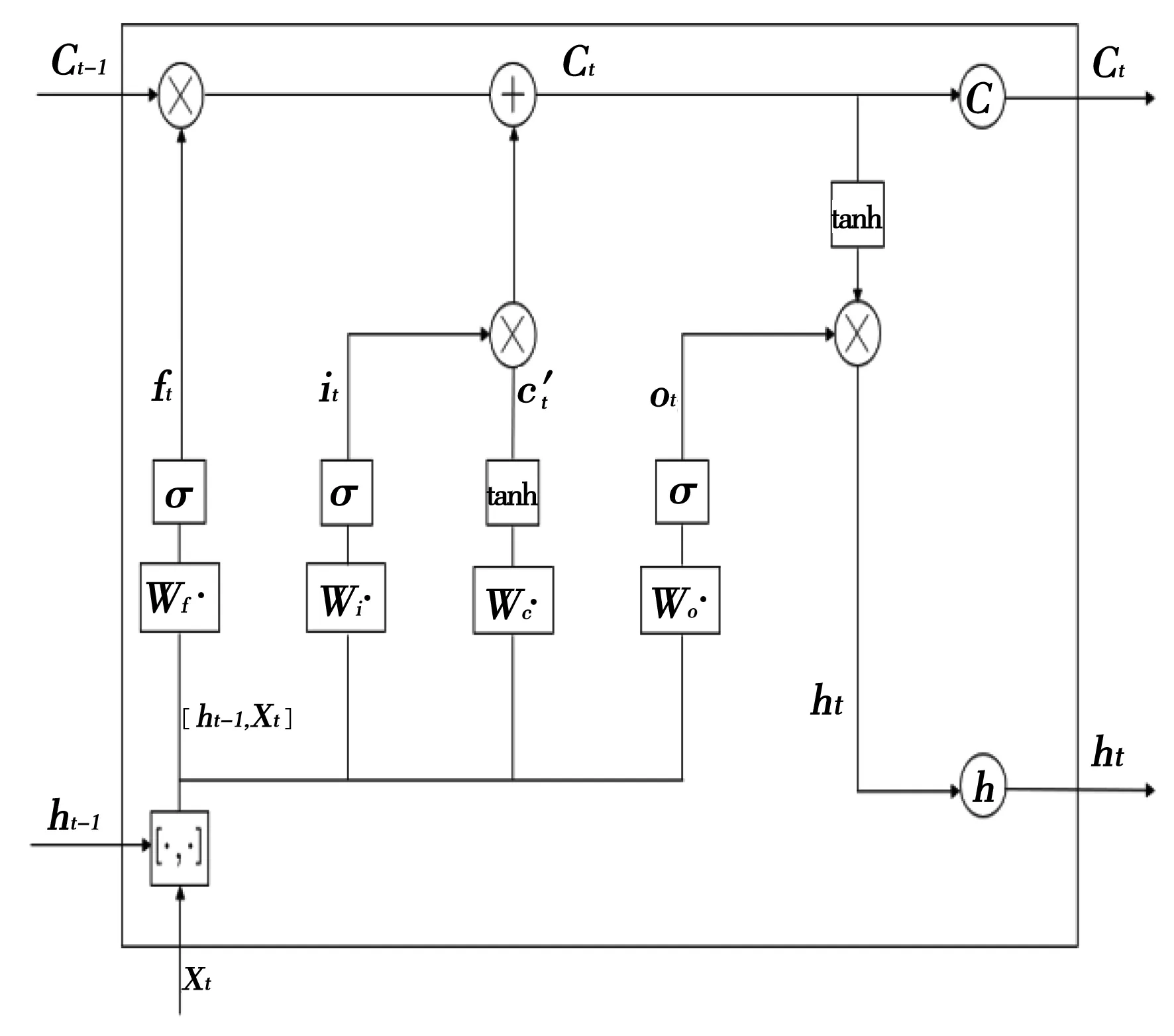
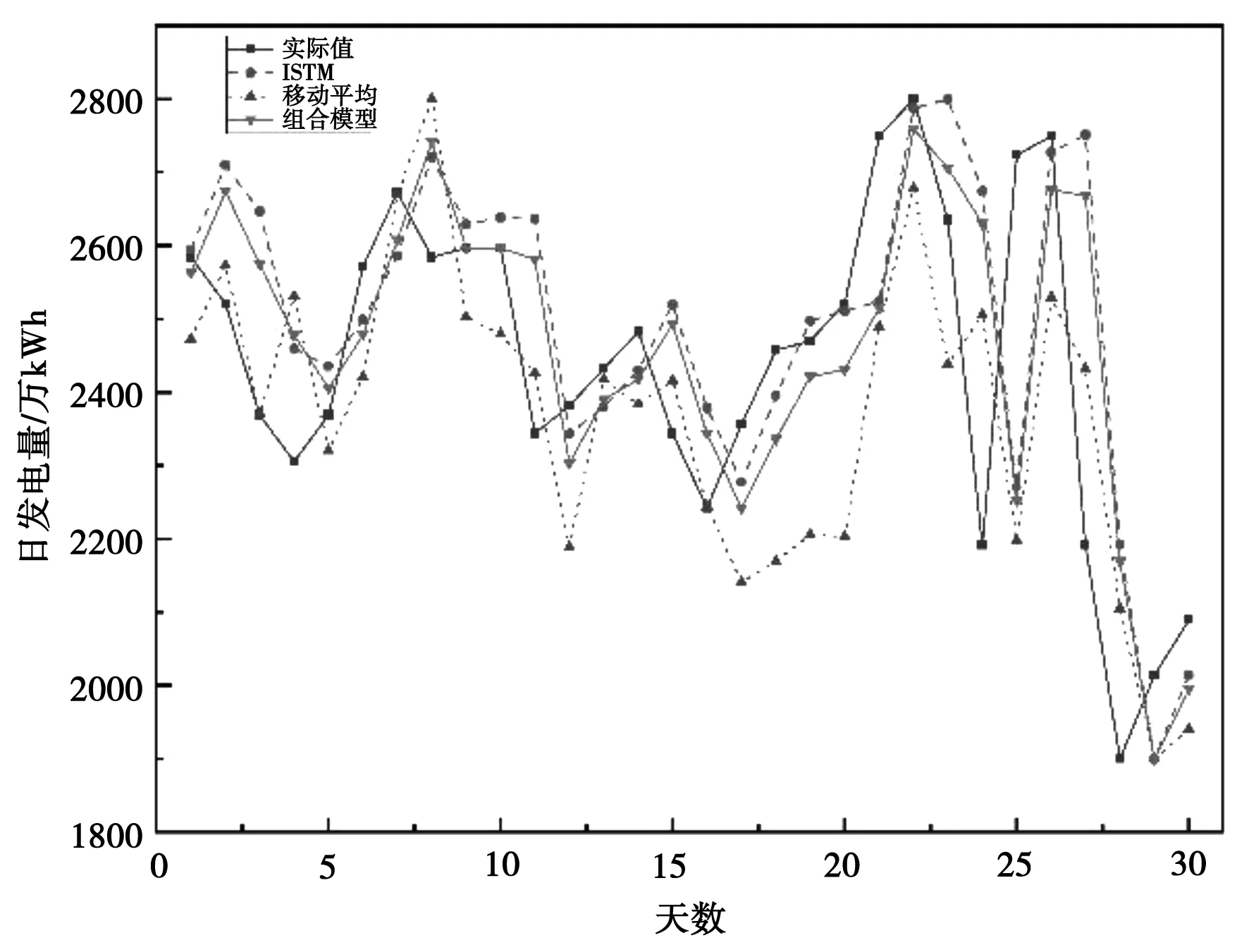
将观测序列设为y1,…,yT,取移动平均的项数N (1) t=N,N+1,… (2) (3) 将前N阶段序列值的平均数作为接下来各阶段的预测值。N的取值区间通常为:200≥N≥5。当往期序列的宏观趋势波动较小,同时序列中无规律振荡发生较多时,N的取值通常取较大值。反之N的取值将取较小值。对于有固定变动周期的序列,通常将周期长度作为移动平均的项数。一般通过比较不同模型之间的预测误差寻找最优N值,最终取预测标准误差较小的模型。 简单移动平均法一般用于短期且目标变化趋势较小的预测,当时间序列产生较大波动时,继续使用该方法所预测的结果将存在较大滞后与误差。 当时间序列的变化趋势波动不大时,通常使用简单移动平均法和加权移动平均法来映射真实趋势。但在时间序列发生不稳定波动时,简单移动平均法及加权移动平均法的局限性会显露出来,预测结果将发生偏差与滞后。为解决该问题,可以使用二次移动平均处理,通过研究分析移动平均法滞后偏差的规律建立预测模型。该方法称为趋势移动平均法。一次移动的平均数的计算公式为: (4) 二次移动平均是连续进行两次移动平均,其计算公式为: (5) 设自某时刻起时间序列的变化趋势为直线趋势,同时在之后的周期里保持该直线趋势进行变化,便将该预测模型设为: (6) 式中:t为目前时期数;T为自t至预测期的时期数;at为截距;bt为斜率。平滑系数由二者组成。 平滑系数受移动平均值数值的影响。通过(6)可得: at=yt yt-1=yt-bt yt-2=yt-2bt … yt-N+1=yt-(N-1)bt 所以 (7) 由式(6),类似式(7)推导,可得 (8) 所以 (9) 推导可得 (10) 于是由式(7)和式(10)可得 (11) 循环神经网络(RNN)是神经网络的一种,一般专门用于时间序列数据的处理,其中长短期记忆网络(LSTM)是循环神经网络(RNN)的一种变种〔6〕。相同统计指标的数据依照发生的先后顺序组合排列形成的数列即为时间序列,时间序列数据通常用来反映某一特定项目在一定时期内的变化趋势。传统的神经网络建立的权连接只涉及不同层之间,RNN相比于传统神经网络的优势在于将权连接建立在了不同层间的神经元之间。对于时间序列的相关问题运用RNN时会取得更好的效果,但是其也存在着一些不足,其中梯度消失的问题最为普遍。针对梯度消失的问题,在增加门限后,LSTM不仅解决了该问题,长期历史数据的记忆能力也有了相应提升,所以LSTM对较长时间跨度的数据信息进行处理有着较好的效果。 图2 LSTM神经网络结构图 循环神经网络LSTM通过遗忘门、输入门、输出门的设置克服了梯度消失的问题。LSTM神经网络的输入门由前一单元的输出ht-1,ct-1和本单元的输入Xt共同构成。将t时刻的输入Xt与前一隐藏层的数据ht-1结合,再通过Wf将其变为与t时刻隐藏层相同的维度,并加入偏置bf后经sigmoid函数进行[0,1]区间内的分类。tanh的作用是保证输入函数的数值维持在[-1,1]的区间内来适配网络,确保它的收敛速度快于sigmoid函数。在LSTM的输出门中,Ct直接作为“记忆”输出至下一单元。经过tanh函数进行运算之后,ht接着与前一时刻的隐藏层与该时刻输入的数据进行乘积运算。LSTM神经网络的计算公式如下所示。 ft=σ(Wf·[ht-1,Xt]+bf) (12) it=σ(Wi·[ht-1,Xt]+bi) (13) (14) (15) ot=σ(Wo·[ht-1,Xt]+bo) (16) (17) 本文所提出的移动平均-LSTM组合预测模型先分别由移动平均及LSTM模型对火电企业发电量进行预测,再赋予不同的权重,最终的预测结果通过二者相加得出〔7〕。权重的值由最小二乘法得出,分别为α1、α2。其中: α1+α2=1 (18) 组合模型的流程图如下图所示。 图3 组合模型流程图 本文以上海市某火力发电企业2018年1月至2020年11月的日发电量数据为训练集,对2020年12月的日发电量进行预测。通过与单一移动平均和LSTM模型的对比得出本文所提出的组合模型具有更高的精确性。 本文选取平均百分比误差作为评价标准,评价标准公式如下: (19) 式中:xi、xi′分别为发电量的预测值及实际值。 在对上述模型进行训练处理后,得出2020年12月1日至12月31日的发电量预测值,并与单一的移动平均模型及LSTM模型的预测值实行比较。结果如图4所示。 图4 预测结果图 本文采用平均百分比误差作为评价标准,来反映不同模型的精确度,结果见表1所示。 表1 预测效果对比 从表1及图4可知,移动平均LSTM组合模型的精度较于单一算法的模型精度有所提高,更加接近实际曲线。 移动平均作为研究时间序列数据的常用工具,本文将其与LSTM神经网络结合,通过对上海市某火力发电企业的历史数据进行分析研究,得出了以下结论: (1)使用趋势移动平均法对历史数据进行处理分析后得出未来一定时间内的预测结果,实验结果证明其具有一定的准确性。 (2)LSTM适合在时间序列建模中使用,其有长时记忆的特点,使用简单,解决了传统长期历史数据序列训练中梯度消失与爆炸的问题。 (3)在接下来的研究中,引入天气、经济增长率等参数,将其作为输入变量,提升模型精确度。 (4)本模型在不同地区的预测精确度还需进一步验证,同时模型对突发事件如疫情的适应性也需进一步的研究。2.2 趋势移动平均法
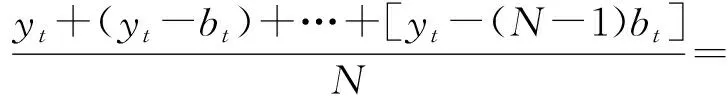
3 LSTM神经网络
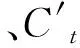
4 移动平均-LSTM组合预测模型

5 实例分析
5.1 实验精度评价
5.2 实验结果

6 结语

