基于分频段前馈补偿的并网变流器输出阻抗校正*

曹建伟 张磊 钱强 张犁 丁勇

基于分频段前馈补偿的并网变流器输出阻抗校正*

曹建伟1张磊1钱强2张犁2丁勇3

(1. 国网湖州供电公司 湖州 313000；2. 河海大学能源与电气学院 南京 211106；3. 南京南瑞继保工程技术有限公司 南京 211102)

并网变流器是分布式发电系统中交直流接口关键设备，为解决弱电网下电网阻抗同并网变流器的交互作用所引起的宽频率范围谐波谐振及系统失稳问题，基于级联系统阻抗模型研究了传统的电网电压单位比例前馈对并网变流器输出阻抗幅相特性的影响，提出基于数字滤波器的电网电压分频段前馈补偿策略，包括减小电网电压前馈低频分量的增益和延迟，增加电网电压前馈高频分量的延迟，并给出前馈补偿回路参数的设计方法，重塑并网变流器输出阻抗为无源特性，提升了并网变流器对电网阻抗宽范围变化的适应能力，实现弱电网下并网系统宽频范围谐波谐振的抑制。仿真和试验验证了理论分析的正确性和所提电网电压分频段前馈补偿策略的有效性。

并网变流器；谐波谐振；弱电网；电网电压前馈

1 引言

并网变流器作为分布式能源同电网间的关键接口，受公共耦合点(Point of common coupling，PCC)电压谐波和时变的电网阻抗影响，并网变流器与弱电网所构成的级联系统面临宽频率范围谐波振荡甚至系统失稳的风险[1-3]，因此提升并网接口变流器输出电流质量及系统稳定性具有重要意义[4]。

电网电压谐波扰动会通过并网变流器输出滤波器产生相应的谐波电流响应，恶化进网电流质量，已有文献主要通过提升电流控制器的幅值增益[5-8]或引入电网电压前馈补偿[9-15]获得较高幅值的并网变流器输出阻抗o，以增强并网系统抗电网电压谐波扰动能力。然而，相关改进控制方法会恶化输出阻抗的相频特性，使得o落于(−90°，+90°)之外，即o呈现负阻、有源特性[16]，不利于提升并网变流器对电网阻抗的适应能力。

从电流控制器优化设计出发，文献[5]提出采用多谐波准谐振控制器以减小进网电流低次谐波分量，但易于使得并网变流器输出阻抗o在谐波频率处表现为负阻特性[6]。附加相角补偿的谐波准谐振控制通过在各次谐波频率处设置零点使得o的相频曲线落于(−90°，+90°)，避免了感性电网阻抗下并网系统失稳风险[7-8]。虽然相关谐振控制器可以有效改善并网系统闭环跟踪的稳态精度，但是相关控制算法对电网电压频率变化较为敏感，数字离散化实现较为繁琐。

基于前馈补偿原理，引入PCC电压前馈通路可以抵消电压谐波扰动的不利影响，加快系统动态响应速度。文献[9]指出PCC电压全前馈虽然显著提升了输出阻抗o的幅值，但前馈通路中微分项的存在易于引入更多的中高频谐波，在此基础上，传统的PCC电压单位比例前馈较好地保留了全前馈对o的低频段幅频特性的贡献，得到了广泛应用[10]。然而，较高的前馈通路增益会恶化o的相频特性，文献[11]进一步提出了PCC电压加权比例前馈，通过选取合适的前馈增益实现o幅频和相频特性的折衷，提升了并网变流器对电网感抗的适应能力。文献[12-14]采用谐波准谐振控制器提取PCC电压中的低次谐波分量，并分别采用有限的谐振控制器个数、前馈环路参数优化设计、自适应前馈方法改善弱电网下并网系统的稳定性。文献[15]提出了基于桥臂电压多重采样的电网电压前馈补偿方案，移除了PCC电压前馈中的电网阻抗压降，有效消除了前馈通路的正反馈作用，但仅适用于单L滤波的并网变流器控制。值得指出的是，现有PCC电压前馈方案较多侧重于o在低频段幅相特性的改善，其对并网变流器高阶滤波器谐振峰的阻尼影响仍有待进一步分析[17-18]。

针对弱电网下并网系统宽频谐振及稳定性问题，现有文献中电网电压前馈补偿方案在实现对电网阻抗适应能力和抗谐波干扰能力时仍较为复杂。本文基于级联系统阻抗模型提出了一种新型电网电压分频段前馈补偿策略，包括减小电网电压前馈低频分量的增益和延迟，增加电网电压前馈高频分量的延迟，并给出了前馈通路数字滤波器参数的详细设计方法，其在实现并网变流器全频段输出阻抗模值提升的同时，保证并网变流器输出阻抗相频落于(−90°，+90°)，较好地兼顾了并网变流器抗电网电压谐波扰动能力和对电网阻抗的适应能力，实现了并网变流器同弱电网端口阻抗的匹配。基于Matlab/Simulink的仿真和试验结果验证了本文所提前馈补偿策略的有效性。

2 电网电压单位比例前馈的负面影响

图1给出了并网变流器的典型电路结构及控制框图，相关参数见表1。其中，i1、Cf、i2组成LCL滤波器，g和g构成电网阻抗g，直流母线电压dc经过正弦脉宽调制(Pulse width modulation, PWM)得到桥臂电压inv，经LCL滤波器得到进网电流g注入阻抗为g的弱电网，ref为电流基准，pcc为并网点电压，c为电容电流有源阻尼系数，f为电网电压前馈通路传递函数，c为电流比例积分调节器(p+i/)，其参数设计依据文献[19]，如式(1)所示。d为数字控制延迟，包含半拍采样延迟和半拍PWM装载延迟[20]，如式(2)所示

式中，p为比例增益，i为积分系数，为数字控制延迟拍数，s为控制周期。

图1 并网变流器基本电路及控制框图

表1 并网变流器参数

根据图1b可知并网变流器输出阻抗o为

图2a给出了表1所示并网变流器在一拍控制延迟下(=1)电网电压前馈系数f变化时输出阻抗的伯德图。当采用传统电网电压单位比例前馈时(f=1)，o1的幅频曲线在低频段(<1 kHz)模值较高，具有较强的抗电网电压基波及低次谐波干扰能力，有助于基波电流跟踪的稳态精度提升，但o1的相频曲线在低频段位于(−90°，+90°)之外，即o1实部为负，呈现有源特性[16]。当电网感抗较大时，如g1(g=3 mH，对应短路比为10)条件下，根据级联系统阻抗稳定性判据可知并网系统易于在幅频曲线交截频率1(720 Hz)处产生谐波振荡[21-22]。

当不采用单位比例前馈时(f=0)，o3的幅频特性在低频段模值有所下降，抗电网电压谐波干扰能力差，但o3相频特性相较于o1有较大改善，全部落于(−90°，+90°)内，表明o3实部在全频段内为正，对复杂电网阻抗适应性强。若改变前馈系数，如f=0.5，可实现输出阻抗幅相特性的折衷，但o2在LCL滤波器谐振频率附近阻抗模值较低，且相位大于90°，即表现为负阻特性，不利于高次谐波 (如2附近)的抑制及容性电网阻抗的接入(如图2a中g2)。

图2b给出了电网电压前馈通路延迟变化时输出阻抗的伯德图，随着延迟逐渐增大，输出阻抗在低频段幅值和相位都略有下降，表明减小低频分量前馈延迟有助于系统抗谐波干扰能力和稳定性的提升。而输出阻抗中高频段幅相特性随着控制延迟变化较为复杂，当增加至2时，幅相特性较为理想，输出阻抗相频曲线落于(−90°，+90°)内，呈现无源特性，但当增加至2.5时，输出阻抗幅相变化较为剧烈，不利于中高频谐振分量的抑制。

图2 Gf和前馈通路延迟变化时并网变流器输出阻抗

3 电网电压前馈分频段补偿策略

3.1 前馈补偿策略的提出

根据第2节分析可知，相较于传统电网电压单位比例前馈(f=1)而言，略微降低前馈通路增益可兼顾并网变流器的输出阻抗模值大小和对电网阻抗的适应能力，降低电网电压前馈低频分量的延迟有助于提升输出阻抗低频段的幅值和相角，合理增加电网电压前馈中高频分量的延迟有助于改善并网变流器输出阻抗在LCL滤波器固有谐振频率r附近的幅相特性。

基于此，本文提出对电网电压前馈补偿环节进行改进，构建了如图3所示基于数字滤波器的分频段前馈补偿策略，其采用式(4)所示的一阶惯性环节f1提取电网电压低频分量，并相应减小低频分量的控制延迟，采用式(5)所示的二阶高通滤波器f2提取电网电压中高频分量，并相应增加中高频分量前馈通路的控制延迟。

式中，1、2分别决定并网耦合点电压pcc的低频和中高频分量前馈通路的增益，l、h分别为低通、高通滤波器转折角频率，1、2分别为低频和中高频分量前馈通路的数字控制延迟拍数。

图3 优化电网电压前馈补偿策略

3.2 前馈补偿参数设计方法

3.2.1 低频前馈通路f1参数设计

电网电压低频分量前馈通路f1用以抵消pcc中低次谐波电压的不利影响，涉及增益1、转折角频率l、控制延迟拍数1的设计。

如图4所示，在数字信号处理器中，电参量的采样和调制波的装载一般发生在三角载波car的波峰或波谷时刻。其中，电参量采样后经过闭环计算生成离散调制波需要一定的延迟时间sd，该采样延迟拍数一般为0.5的整数倍，其同离散调制波等效的零阶保持器半拍延迟共同构成数字控制延迟，因此，前馈通路延迟1最小为1。由于降低低频分量前馈通路延迟有助于提升输出阻抗o模值，故选取1为1。

图4 数字控制延迟说明

对于l而言，一方面，pcc主要含有6±1次谐波(为正整数)，频率越高，谐波电压含量较低，若对19次以内的低频谐波进行前馈，则转折角频率l应大于2π∙950 rad/s；另一方面，转折角频率还应尽可能小于LCL滤波器固有谐振角频率r。为避免电网电压电压前馈通路f1和f2的交互影响，应选取较低的l，本文取为2π∙1 000 rad/s。

根据图2a可知，增益1的选择需要折衷考虑输出阻抗在低频段的幅值和相角，以兼顾抗电压谐波干扰能力和对电网阻抗的适应能力。由于并网变流器需要适应SCR为10的弱电网[23]，即需要考虑适应g约为3 mH的感性电网，根据级联系统阻抗稳定性判据可知，输出阻抗o与电网阻抗g的幅频曲线交截频率c处o的相位应大于−90°，若取45°相角裕度，1的选取应满足式(6)

式中，∆Mag定义为o与g在幅频曲线交截频率c处的幅值差，∆Phase定义为o与g的相角差，且考虑相角裕度为45°。

图5中实线和虚线分别给出了电网电压低频分量前馈通路增益1由0.2增加至0.8时，∆Mag和∆Phase随频率变化的数学关系，可以发现幅频曲线的交截频率c随低频分量前馈增益1增大而增大，且1≤0.6时，∆Phase在c处的相角大于0°，即表明此时并网变流器弱电网级联系统具有大于45°的相角裕度，考虑到为保证良好的抗低次电压谐波能力，1应尽可能取较大值，本文选取1为0.6。

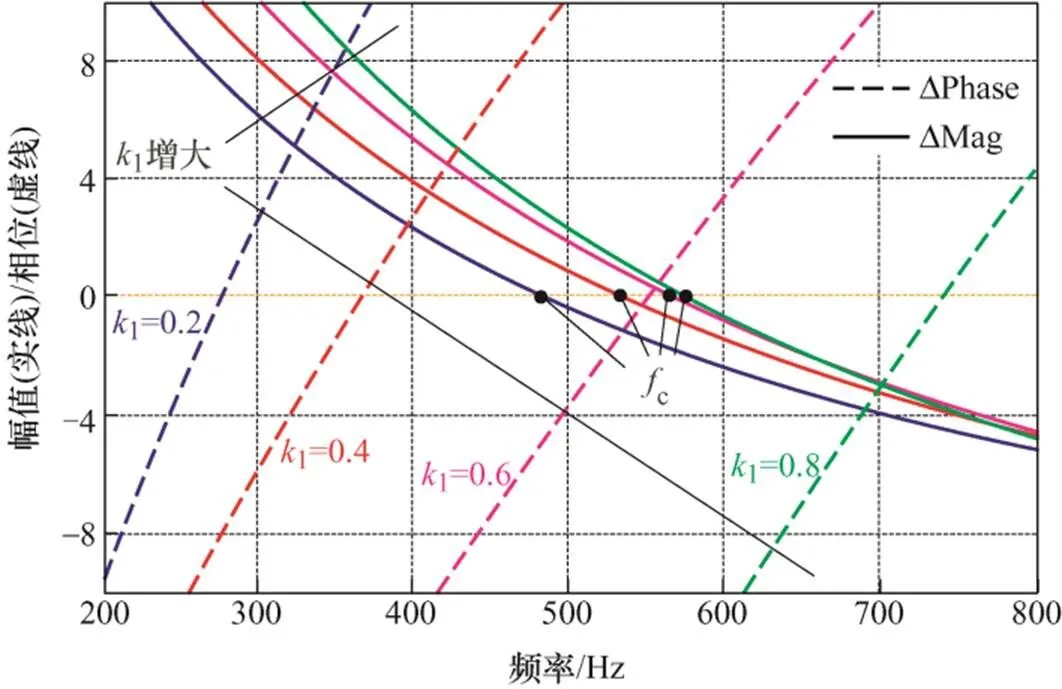
图5 低频前馈通路增益k1变化时对∆Mag、∆Phase的影响

3.2.2 中高频前馈通路f2参数设计

电网电压中高频分量前馈通路f2用以改善o在r附近的幅频特性，即提升o在r处的模值，重塑o在r附近为无源特性，即保证o的相位落于(−90°，+90°)区间内。

转折角频率2一方面应大于1，以减小对前馈通路f1的影响，另一方面应小于r，避免对r附近pcc分量的衰减，即1≤2≤r，本文取2为0.5(r+1)=2π∙2 215 rad/s。

为实现LCL固有谐振频率r附近谐振分量的抑制，pcc前馈中的中高频分量的相位需要在−180°附近，才可形成闭环负反馈，因此高通滤波器f2在r附近的相移需要设计为滞后180°。

图6给出了f2中控制延迟2变化时f2的伯德图，可以看出随着2增大，f2在中高频段相位滞后逐渐增大，当2为2.5时，f2在r附近相位接近−180°，即可实现中高频分量的闭环负反馈。

图6 前馈通路延迟λ2变化时Gf2的伯德图

图7展示了电网电压中高频分量前馈通路增益2变化时并网变流器输出阻抗o实部Re[o]的频率特性，随着2增大，LCL谐振频率附近逐渐呈现负阻特性，即不利于高频谐振分量的抑制，当2≤0.7时，Re[o]在全频段内为正，即并网变流器具有无源特性[18]。综合考虑2～4 kHz频段o的阻尼特性，本文取2为0.6。

图7 前馈通路增益k2变化时输出阻抗Zo实部

图8展示了采用所提优化电网电压前馈补偿策略的变流器输出阻抗op的伯德图，可以看出op的相频曲线落于(-90°，90°)区间内，呈现无源特性，在感性电网阻抗g1(SCR为10)条件下，阻抗幅频曲线交截频率1(540 Hz)处相角裕度为45°，在容性电网阻抗g2(传统单位比例前馈存在高频谐振风险) 条件下，阻抗幅频曲线交接频率2(4.7 kHz)处系统相角裕度为20°。因此，两种电网阻抗下并网系统均具有一定的相角裕度，不易于激起谐波谐振，基于所提前馈补偿策略的并网变流器可适应更复杂的电网阻抗。

图8 采用优化电网电压前馈补偿策略的输出阻抗

4 仿真与试验

为验证所提电网电压分频段前馈补偿策略用于抑制并网变流器同弱电网谐波交互作用的有效性，基于一台5 kW单相T型并网变流器进行仿真和试验验证，相关硬件和控制参数如第2节中表1所示。

首先，为验证所提分频段前馈补偿策略的有效性，在Matlab/Simulink中搭建了仿真模型，并采用频谱网络分析仪Venable 3120，对并网变流器输出阻抗在100 Hz～10 kHz频段内分别进行了仿真和试验测试，阻抗测量的基本结构如图9所示。

图9 输出阻抗仿真和试验测量结构框图

图10给出了输出阻抗理论曲线op(实线)和阻抗扫频测试结果op-m(各扫频点记为“o”)，图11给出了输出阻抗试验扫频测量和理论曲线对比。根据图10和图11可知，理论、仿真和试验曲线在全频段内都较好地匹配，且输出阻抗相频曲线在全频段内位于(-90°，90°)区间内，即表明所提前馈补偿策略可实现变流器输出阻抗无源特性的重塑，根据级联系统阻抗稳定性判据可知并网变流器对复杂电网阻抗适应能力得以提升。

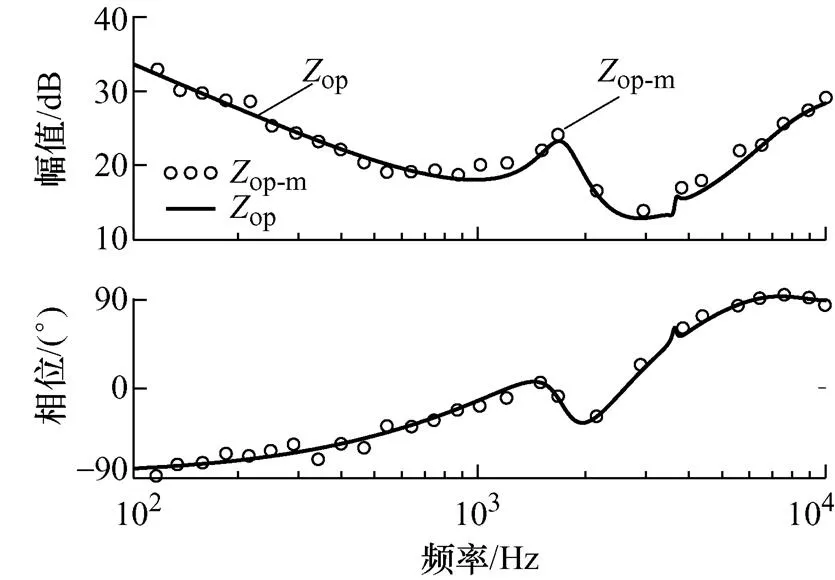
图10 采用优化前馈补偿策略的输出阻抗仿真测量

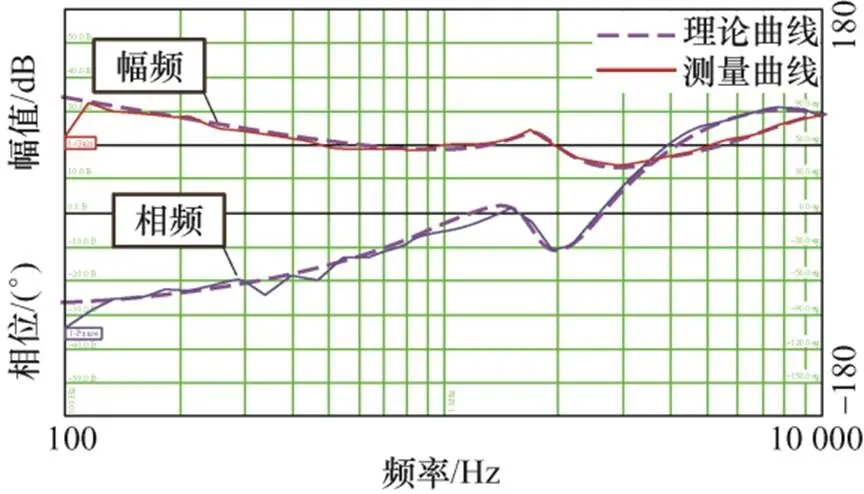
图11 采用优化前馈补偿策略的输出阻抗试验测量

然后，与理论分析工况保持一致，分别在感性电网阻抗(g1，3 mH)、容性电网阻抗(g2，0.45 mH//7 μF)下对基于不同电网电压前馈补偿策略的并网变流器进行试验测试。

图12a和12b分别给出了感性、容性阻抗下基于传统电网电压单位比例前馈的并网变流器试验波形。其中，图12a感性电网阻抗g1下，进网电流g傅里叶分解表明含有大量700 Hz的谐波成分，与图2a中o1和g1幅频曲线交截频率1相吻合。图12b容性电网阻抗g2下，g含有较多高频谐波4.7 kHz成分，同图2a中o1和g2幅频曲线交截频率2相接近。图12表明采用传统比例前馈的并网变流器在不同电网阻抗下存在谐波谐振问题。

图12 Gf和前馈通路延迟变化时并网变流器输出阻抗

图13a和13b给出了感性、容性电网阻抗下采用所提电网电压分频段前馈补偿策略的并网变流系统试验波形。可见，当电网阻抗特性变化时，进网电流g正弦度较好，g的频谱分析表明图8中阻抗幅频曲线交截频率1、2处的谐波含量较低，即所提前馈策略能够抑制并网变流器同电网的谐波交互作用，改善复杂电网条件下并网变流器稳定性。

图13 不同电网阻抗下采用优化前馈补偿试验波形

5 结论

降低电网电压前馈低频分量的延迟有助于提升输出阻抗低频段的幅值和相角，合理增加电网电压前馈分量中高频分量延迟可改善LCL滤波器谐振频率附近的幅相特性。基于一阶低通滤波器和二阶高通滤波器的电网电压分频段前馈补偿策略可有效重塑输出阻抗为无源特性，解决电网阻抗同并网接口变流器交互作用引起的宽频率谐波谐振问题。

[1] 樊陈，姚建国，张琦兵，等．英国“8∙9”大停电事故振荡事件分析及思考[J]．电力工程技术，2020，39(4)：34-41．

FAN Chen，YAO Jianguo，ZHANG Qibing，et al. Reflection and analysis for oscillation of the blackout event of 9 August 2019 in UK[J]. Electric Power Engineering Technology，2020，39(4)：34-41.

[2] WANG K，YUAN Y B，GENG Y W，et al．A practical structure and control for reactive power sharing in microgrid[J]. IEEE Transactions on Smart Grid，2019，10(2)：1880-1888．

[3] 阮正鑫，张逸，张嫣，等. 高比例光伏与配电网超高次谐波交互影响研究[J]．电力工程技术，2021，40(2)：18-25．

RUAN Zhengxin，ZHANG Yi，ZHANG Yan，et al. Interaction of high proportion photovoltaic and supraharmonic in distribution network[J]. Electric Power Engineering Technology，2021，40(2)：18-25.

[4] 钱强，谢少军，季林，等. 一种提升逆变器对电网适应能力的电流控制策略[J]. 中国电机工程学报，2016，36(22)：6193-6201.

Qian Qiang，XIE Shaojun，JI Lin，et al. A current control strategy to improve the adaptability to utility for inverters[J]. Proceedings of the CSEE，2016，36(22)：6193-6201.

[5] 黄鹏，戴威，张莹，等. 兼具有源电力滤波器功能的多功能并网逆变器控制[J]．电力工程技术，2021，40(1)：107-114．

HUANG Peng，DAI Wei，ZHANG Ying，et al. Multi-function grid-connected inverter control with APF function[J]. Electric Power Engineering Technology，2021，40(1)：107-114.

[6] XIE C，LI K，ZOU J X，et al. Passivity-based stabilization of LCL-type grid-connected inverters via a general admittance model[J]. IEEE Transactions on Power Electronics，2020，35(6)：6636-6648．

[7] ALI A, HARMID R, JUAN C，et al. Passivity-based design of plug-and-play current-controlled grid-connected inverters[J]. IEEE Transactions on Power Electronics，2020，35(2)：2135-2150.

[8] BAO X，KE G，MAO M X，et al. Analysis and improved design of phase compensated proportional resonant controllers for grid-connected inverters in weak grid[J]. IEEE Transactions on Energy Conversion，2020，35(3)：1453-1464.

[9] WANG X，RUAN X，LIU S，et al. Full feedforward of grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics[J]. IEEE Transactions on Power Electronics，2010，25(12)：3119-3128.

[10] LIU B Y，WEI Q K，ZOU C Y，et al. Stability analysis of LCL-type grid-connected inverter under single-loop inverter-side current control with capacitor voltage feedforward[J]. IEEE Transactions on Industrial Informatics, 2018，14(2)：691-702．

[11] QIAN Q，XIE S J，XU J M，et al. Passivity-based output admittance shaping of the converter-side current- controlled grid-tied inverter to improve the robustness to the grid impedance[J]. IET Power Electronics，2020，13(10)：1956-1965.

[12] 徐飞，汤雨，谷伟. 弱电网条件下LCL型并网逆变器谐振前馈控制策略研究[J]．中国电机工程学报，2016，36(18)：4970-4981．

XU Fei，TANG Yu，GU Wei. Resonant feedforward control strategy for LCL-type grid-connected inverters in weak grid condition[J]. Proceedings of the CSEE，2016，36(18)：4970-4981.

[13] 王翰文，曾成碧，苗虹. 基于多谐振电网电压前馈的并网逆变器相位补偿算法研究[J]. 电力系统保护与控制，2021，49(18)：81-89.

WANG Hanwen，ZENG Chengbi，MIAO Hong. A phase compersation algorithm of a grid-connected inverter based on a feedforward multi-resonant grid voltage[J]. Power System Protection and Control，2021，49(18)：81-89.

[14] LIN Z H，RUAN X B，WU L G，et al. Multi-resonant component-based grid-voltage-weighted feedforward scheme for grid-connected inverter to suppress the injected grid current harmonics under weak grid[J]. IEEE Transactions on Power Electronics，2020，35(9)：9784-9793．

[15] XU J M，XIE S J，QIAN Q，et al．Adaptive feedforward algorithm without grid impedance estimation for inverters to suppress grid current instabilities and harmonics due to grid impedance and grid voltage distortion[J]. IEEE Transactions on Industrial Electronics，2017，64(9)：7574-7586．

[16] LENNART H，WANG X F，ALEJANDRO G Y，et al. Passivity-based stability assessment of grid-connected VSCs：An overview[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics，2016，4(1)：116-125.

[17] WANG X H，QIN K，RUAN X，et al. A robust grid-voltage feedforward scheme to improve adaptability of grid-connected inverter to weak grid condition[J]. IEEE Transactions on Power Electronics，2021，36(2)：2384-2395.

[18] HE Y Y，WANG X H，RUAN X B，et al. Hybrid active damping combining capacitor current feedback and point of common coupling voltage feedforward for LCL-type grid-connected inverter[J]. IEEE Transactions on Power Electronics，2021，36(2)：2373-2383.

[19] XU J M，XIE S J，TANG T. Evaluations of current control in weak grid case for grid-connected LCL-filtered inverter[J]. IET Power Electronics，2013，6(2)：227-234.

[20] LI X Q，FANG J Y，TANG Y，et al. Capacitor-voltage feedforward with full delay compensation to improve weak grids adaptability of LCL-filtered grid-connected converters for distributed generation systems[J]. IEEE Transactions on Power Electronics，2018，33(1)：749-764.

[21] SUN J. Impedance-based stability criterion for grid-connected inverters[J]. IEEE Transactions on Power Electronics，2011，26(11)：3075-3078.

[22] 王利超，于永军，张明远，等. 直驱风电机组阻抗建模及次同步振荡影响因素分析[J]．电力工程技术，2020，39(1)：170-177．

WANG Lichao，YU Yongjun，ZHANG Mingyuan，et al. Impedance model and analysis of subsynchronous oscillation influence factors for grid-connected full-converter wind turbines[J]. Electric Power Engineering Technology，2020，39(1)：170-177.

[23] 吴恒，阮新波，杨东升，等. 弱电网条件下锁相环对LCL型并网逆变器稳定性的影响研究及锁相环参数设计[J]. 中国电机工程学报，2014，34(30)：5259-5268．

WU Heng，RUAN Xinbo，YANG Dongsheng，et al. Research on the stability caused by phase-locked loop for LCL-type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE，2014，34(30)：5259-5268.

Frequency-dependent Feedforward Compensation for Reshaping the Output Impedance of Grid-connected Converter

CAO Jianwei1ZHANG Lei1QIAN Qiang2ZHANG Li2DING Yong3

(1. State Grid Huzhou Power Supply Company, Huzhou 313000;2. College of Energy and Electrical Engineering, Hohai University, Nanjing 211106;3. NARI Electric Co., Ltd., Nanjing 211102)

Grid-connected converter is acting as the critical AC/DC interface in distributed power generation system. Aiming at solving the harmonic resonance over the wide-frequency band and the system instability problem caused by interactions between the grid impedance and the grid-connected converter, the influence of the traditional unit grid voltage feedforward (GVF) compensation on the magnitude-phase characteristic through the cascaded impedance model is revealed. The frequency-dependent feedforward compensation strategy based on the digital filter is further proposed, which includes the reduction of the gain and the delay of the low-frequency component of the grid voltage, and the increase of the delay of the high-frequency component of the grid voltage. The design guideline of the feedforward parameters is further elaborated, which reshapes the inverter output impedance to be passive. The adaptability to the variation of the grid impedance is enhanced, and the wide-frequency band harmonics under the weak grid are also suppressed. Simulation and experimental results finally verify the correctness of the theoretical analysis and the effectiveness of the proposed frequency-dependent GVF compensation strategy.

Grid-connected converter；harmonic resonance；weak grid；grid voltage feedforward

10.11985/2021.04.017

TM46

* 国网浙江省电力公司科技(2019-HUZJTKJ-14)、江苏省自然科学基金青年基金(BK20200510)和中央高校基本科研业务费专项资金(B200201022)资助项目。

20210607收到初稿，20210717收到修改稿

曹建伟，男，1978年生，工程师。主要研究方向为新能源并网运行与控制。E-mail：cjianwei1978@126.com

钱强(通信作者)，男，1992年生，博士，讲师。主要研究方向为并网变流器控制。E-mail：qianqiang@hhu.edu.cn

张犁，男，1985年生，博士，教授。主要研究方向为新能源电力变换装备及运行控制。E-mail：zhanglinuaa@hhu.edu.cn