基于多目标均衡优化的设计洪水推求方法

黄成剑， 解阳阳， 刘赛艳， 沈 腾

(扬州大学 水利科学与工程学院， 江苏 扬州 225009)

1 研究背景

设计洪水是指符合特定防洪标准的洪水过程，是防洪规划设计的重要依据[1]。在实际的防洪风险评估中，大型水库的防洪标准往往很高，可达到1 000年一遇或10 000年一遇等。然而，目前水文频率分析法的精度不高，难以满足水库入库洪水设计的需求[2]。因此，有必要采用合理的方法推求水库的入库设计洪水。

由于洪水的发生时间及过程存在随机性，很难根据洪水的统计规律推求出一定频率的洪水过程线。我国多采用放大典型洪水过程线的方法(即典型洪水放大法)推求设计洪水[3]。对于洪水峰、量同时影响防洪效果的水利工程，常采用同频率法推求设计洪水。当峰、量关系较差时，采用同频率法会因各时段放大倍比差异，导致洪水过程线在时段衔接处出现突变。传统的手动修匀方式在很大程度上增加了设计洪水推求过程的复杂性[4]，针对同频率法的修匀问题，许多学者提出了改进策略，如张彦洪[5]提出同频率直接放大法，可直接放大典型洪水过程线，减少了复杂的修匀步骤。还有些学者将优化算法引入设计洪水计算，如董四方等[6]采用混沌粒子群算法(chaos-particle swarm optimization, COSPSO)求解设计洪水放缩模型；段春青等[7]采用改进粒子群算法建立设计洪水放缩模型。以往的改进方法虽然取得了较好的成效，但也存在一定的局限性。具体而言，同频率直接放大法相比修匀计算的同频率法，计算结果偏差较大；基于优化算法的设计洪水放缩模型也常因惩罚因子的选取而呈现较大的不确定性。因此，如何有效简化计算过程，减小方法中不确定性因素的影响，是改进现有设计洪水推求方法的一个重要方向。

系统的均衡和优化是系统科学和系统工程研究的重要问题[8]。系统均衡和优化思想在水资源系统中发挥着日益重要的作用[9-10]。为了克服现有设计洪水推求方法修匀繁琐、随机性强等缺点，本研究将系统均衡和优化思想用于解决设计洪水的推求问题，提出一种新的设计洪水推求方法，即多目标均衡优化法。具体而言，该方法基于不同设计洪水要素构建洪水设计误差指标向量(简称“误差向量”)，根据该误差向量进一步建立多目标均衡优化模型，并采用优化算法对该模型进行求解，直接得到满足一定设计标准的洪水过程线。总体而言，该方法能使设计洪水较好地保持典型洪水过程线的形状，无需手动修匀计算或反复调整算法参数，大大减少了计算的复杂性和不确定性，可为设计洪水的推求提供有价值的参考。

2 数据来源与研究方法

2.1 研究区概况

黄河兰州上游流域是整个黄河流域的主要产水区，其多年平均径流量达316×108m3，占整个黄河流域多年平均径流量的56.4%。近年来，黄河上游流域极端气候事件频发，洪水风险呈现一定的增加趋势[11-12]。

本研究以黄河兰州上游流域的刘家峡水库为研究对象。该水库是一座以防洪为主，同时兼顾发电、灌溉、防凌等综合效益的年调节水库。刘家峡水库的防洪调度直接关系到其下游兰州市及水电站的防洪安全。在黄河上游洪水风险增加的背景下，准确地推求刘家峡水库的入库设计洪水，为该水库的防洪调度提供科学依据，具有重要的现实意义[13]。

2.2 数据来源

1964和1967年的洪水是黄河兰州上游自有可靠观测数据以来的两场特大洪水，它们的重现期都接近100年一遇，具有洪量大、历时长等特点[14]。此外，这两场典型的实测洪水还是黄河上游大型水库防洪安全设计的重要依据[12,15]。因此，本研究采用这两场洪水的流量数据来推求刘家峡水库的设计洪水。

这两场洪水的流量数据分别来自1964和1967年的《中华人民共和国水文年鉴：(第4卷 黄河流域水文资料)》，数据的可靠性能够得到保障。

2.3 研究方法

2.3.1 同频率直接放大法 同频率直接放大法是一种能够直接推求设计洪水过程线的方法，它的基本原理是根据设计标准下的洪峰流量和时段洪量，分段推求设计洪水过程线[5]。为了避免繁琐的修匀计算而直接得出计算结果，该方法在时段衔接点处取短时段放大倍比进行计算。例如，在最大1 d和最大3 d洪量分界点处，采用最大7 d的放大倍比计算。以历时7 d的洪水为例，其计算步骤如下：

首先，根据洪水峰、量关系确定洪峰或最大1 d洪量的放大倍比，分别如公式(1)、(2)所示。

(1)

(2)

式中：KQm和K1分别为洪峰和最大1 d洪量的放大倍比；Qmp和Qmax分别为特定频率设计洪水和待推求设计洪水的洪峰流量，m3/s；W1p和W1分别为特定频率设计洪水和待推求设计洪水的最大1 d洪量，m3。

其次，根据时段洪量差推导最大3 d的洪量放大倍比K3，同理可得最大7 d的洪量放大倍比K7(见公式(3)、(4))。因篇幅所限，放大倍比的推导步骤和部分洪量的计算公式可参考文献[5]，本研究不再赘述。

最后，根据放大倍比按先短时段后长时段放大的顺序推求设计洪水。

以3时段洪水为例，设典型洪水过程线上最大7 d洪量对应的流量变化过程为Q7，1，Q7，2，…，Q7，i，Q3，1，Q3，2，…,Q3，j，Q1，1，Q1，2，…,Q1，m，Q3，j+1，Q3，j+2，…,Q3，j+n，Q7，i+1，Q7，i+2，…,Q7，i+r，见图1。

(3)

(4)

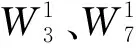
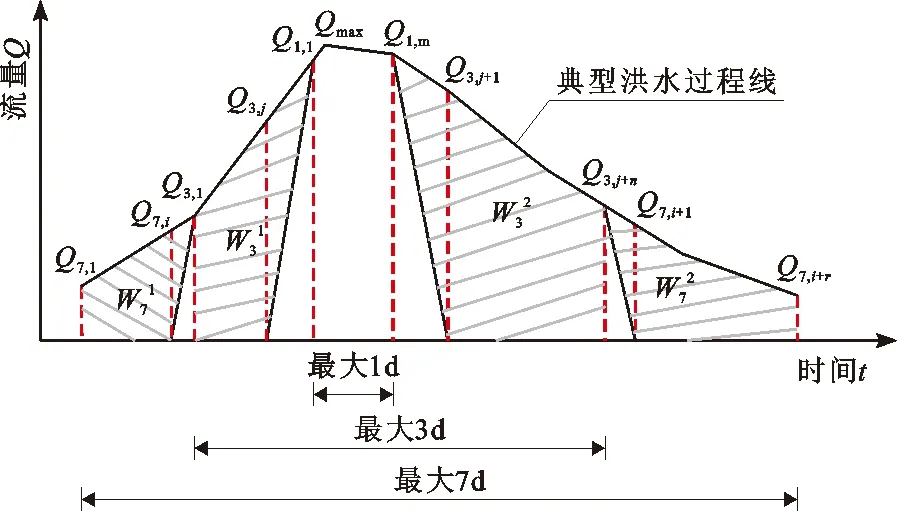
图1 典型洪水的部分过程线及洪量示意图[5]

2.3.2 罚函数法 罚函数法是将洪水放大过程归纳为一个带约束的极值优化问题，在保证峰、量的前提下，尽量使放大后的洪水保持典型洪水的过程线形状。在构建设计洪水放缩模型时，以设计洪水与典型洪水斜率离差之和最小化为目标，以待推求设计洪水峰、量等于设计值为约束条件。为了便于求解该模型，通常将约束条件转换成罚函数的形式[16]，目标函数如公式(5)所示。在求解基于罚函数法建立的设计洪水放缩模型时，需要根据经验选取惩罚因子，然而在实际计算中惩罚因子的选取很难把握[17]。若惩罚因子过小，则难以起到约束作用；若惩罚因子过大，则会导致结果出现较大的偏差，需要反复调整参数进行计算。

w1|Qmax-Qmp|+w2|W1d-W1p|+w3|W3d-W3p|+w4|W7d-W7p|

(5)

式中：m为离散点数量；Qp(i)和Q(i)分别为待推求设计洪水和典型洪水第i时段的流量，m3/s；Qmax为待推求设计洪水的洪峰流量，m3/s；Qmp为设计标准对应的洪峰流量，m3/s；W1d、W3d、W7d分别为1、3、7 d洪量，m3；W1p、W3p、W7p分别为设计标准对应的1、3、7 d洪量，m3；w1、w2、w3、w4为惩罚因子。

2.3.3 多目标均衡优化法 均衡和优化分别代表着系统的两种发展状态，均衡表示系统内的各项要素能够稳定、平衡地发展，而优化代表系统内的各项要素能够朝着有利的方向发展。将均衡与优化两者结合起来旨在使系统能够在均衡条件下，通过优化实现整体朝着有利的方向发展[18-19]。多目标均衡优化法正是基于这一理论所提出的。

采用优化方法推求设计洪水在本质上是一个多目标优化问题，待推求设计洪水既要保证洪峰和时段洪量满足设计标准，又要尽量保持典型洪水过程线形状，但洪水峰、量、形之间又存在着一定的矛盾。在求解此类问题时，一般的罚函数法会侧重于某项指标的优化而忽略了整体的均衡。多目标均衡优化法在误差向量的基础上建立相应的均衡优化模型，通过优化算法求解该模型，实现设计洪水朝着有利方向整体优化、均衡优化。其中，误差向量由洪峰误差、洪量误差和形状误差等3项指标共同构成，误差向量表示如下：

A=[f1,f2,f3,f4,f5]

(6)

(7)

式中：f1表示洪峰误差，f1越小则推求设计洪水洪峰越接近设计值；f2、f3、f4表示各时段洪量误差，f2、f3、f4越小则推求设计洪水洪量越接近设计值；f5表示形状误差，f5越小则推求设计洪水形状越接近典型洪水形状；r为待推求设计洪水与典型洪水的Pearson相关系数；其余变量含义同前文。

根据误差向量建立均衡优化目标函数如公式(8)所示。该目标函数由两部分组成，前半部分用于控制误差向量的平均值最小，后半部分用于控制误差向量的标准差最小。

minf=mean(A)+σ(A)

(8)

式中：mean()为向量各元素的平均值；σ()为向量各元素的标准差。

在公式(8)中，平均值最小化有利于保证误差向量中各项指标尽可能地小，标准差最小化有利于保证误差向量中各项指标的均衡变化，这样既减少了设计洪水峰、量、形的误差，又兼顾了不同类误差的协调性，可以实现设计洪水的均衡优化。此外，该目标函数将约束条件引入误差向量，从而避免了惩罚因子的选取，可有效减弱计算过程的不确定性。

我国医生由于医疗资源紧缺，工作负荷大，加之职业环境紧张，职业倦怠情况严重[4-6]。本文旨在通过了解美国医生职业倦怠的状况，分析美国医生职业倦怠管理的问题，为中国医生职业倦怠管理提供参考依据。

多目标均衡优化法的具体计算步骤如下，计算流程如图2所示。

(1)选取典型洪水过程线。

(2)根据特定频率下的洪水峰、量特征值Qmp、W1p、W3p、W7p及典型洪水的峰、量特征值Qmax、W1d、W3d、W7d计算放大倍比k1、k2、k3、k4。

(3)以放大倍比k为优化变量，将放大倍比的范围初定为[min(ki), max(ki)]，并在此基础上添加拓展系数β1和β2扩大种群个体的搜索范围，在[β1min(ki),β2max(ki)]区间内随机生成初始解。在本研究中，β1=0.9，β2=1.1。

(4)根据典型洪水过程流量Qp和随机生成的k的初始解，计算设计洪水流量Q，并按公式(6)和(7)构建误差向量。

(5)以公式(8)作为优化目标，采用优化算法求解，在满足算法终止条件后得到各时段的放大倍比kbest。

(6) 根据kbest放大典型洪水过程，推求设计洪水过程线。

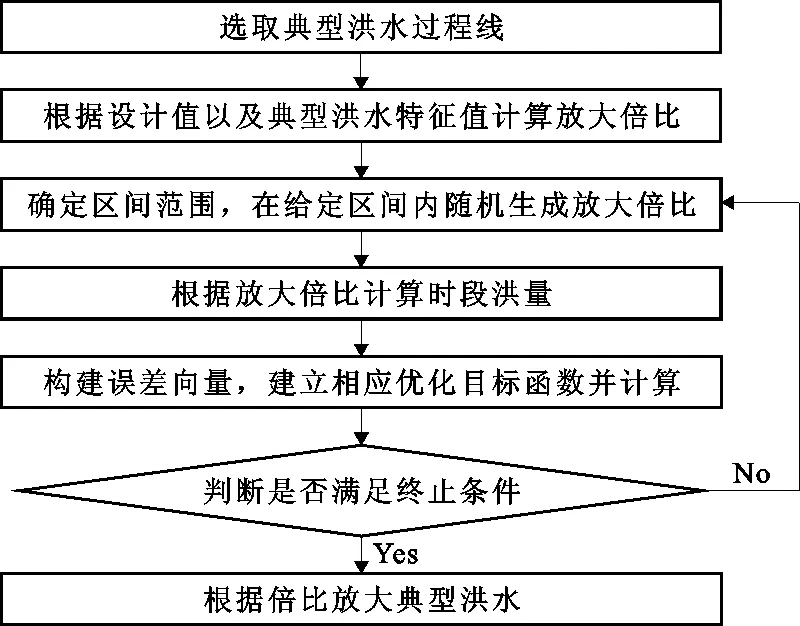
图2 多目标均衡优化法计算流程图

2.4 设计洪水推求方法的评价

在推求设计洪水时，通常选取典型年份的洪水过程，并根据相应设计标准放大典型洪水过程线。因此，可根据上述步骤，构建如图3所示的指标体系。评价指标为2.3.3节所提出的洪峰误差、洪量误差和形状误差，具体见公式(7)。

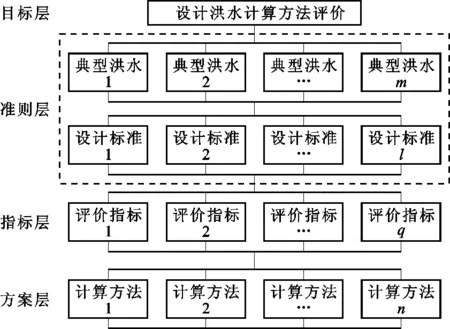
图3 设计洪水推求方法的综合评价指标体系框架

在本研究中，下层要素相对上层要素的重要性以及各层要素间的重要性均相同，其具体计算步骤如下：

(1)将各方法所得计算结果转换为具体评价指标。由于各评价指标均是以相对误差的形式表达，故无需进行归一化处理，指标值越小表示方案越优。

(2)由图3准则层与指标层之间的关系可知，每种方法有m个典型年，每个典型年有l种设计标准，各设计标准下又有q项评价指标，故每种方法共计m×l×q项评价指标。考虑到各层各指标间具有相同重要性，可直接采用公式(9)计算各方法的综合评价指标e。

(9)

式中：e为综合评价指标；i为典型年的个数；j为设计频率的个数；k为评价指标的个数；f为具体评价指标值。

(3) 根据综合评价指标e，选取最优方案，e值越小则表示方案越优。

3 结果与分析

选取黄河兰州上游1964和1967年典型洪水过程，依据前文介绍的研究方法分别在4种设计频率下推求刘家峡水库的入库设计洪水。典型洪水的历时为45 d，计算时段为1 d，典型洪水特征值和特定频率设计值[21]如表1所示。

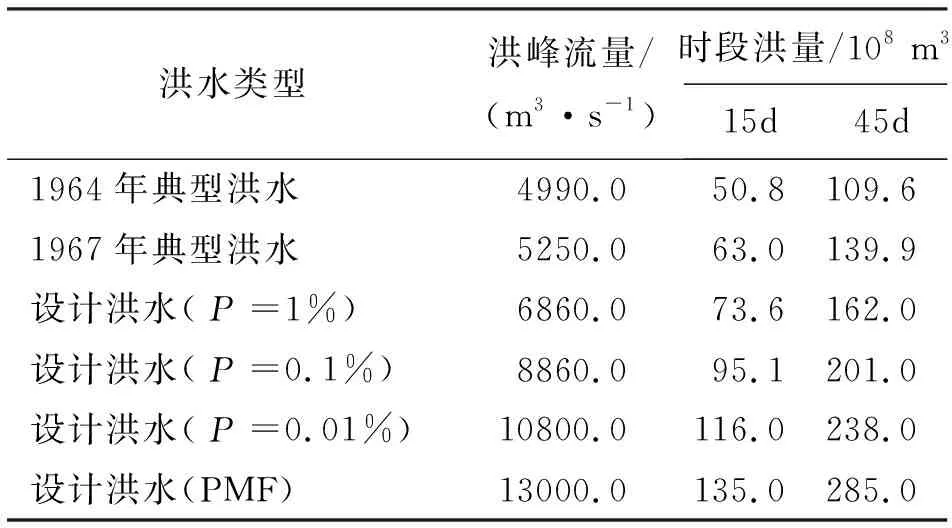
表1 刘家峡水库典型洪水和设计洪水特征值

布谷鸟算法(cuckoo search, CS)是通过模拟布谷鸟的Lévy飞行特征来搜索最优解的优化算法[22]。该算法具有搜索机制简单、调整参数较少、寻优能力较强等优点。改进布谷鸟算法(improved cuckoo search, ICS)在CS算法的基础上引入了动态发现概率以及变异机制，具有更高的搜索效率和更稳定的寻优结果[23]。本研究统一采用ICS算法求解罚函数法模型和多目标均衡优化法模型，以获取相应的设计洪水。在求解多目标均衡优化法模型和罚函数法模型时，ICS算法的适应度函数分别为公式(8)和(5)。ICS算法参数设置为：最大迭代次数Tmax=2 000，种群规模Npop=50，其中罚函数法的惩罚因子经多次试算取w1=10、w2=w3=600。基于1964和1967年两场典型洪水和3种典型洪水放大方法(同频率直接放大法、罚函数法和多目标均衡优化法)的洪水推求误差如表2和3所示，相应的设计洪水过程线如图4和5所示。

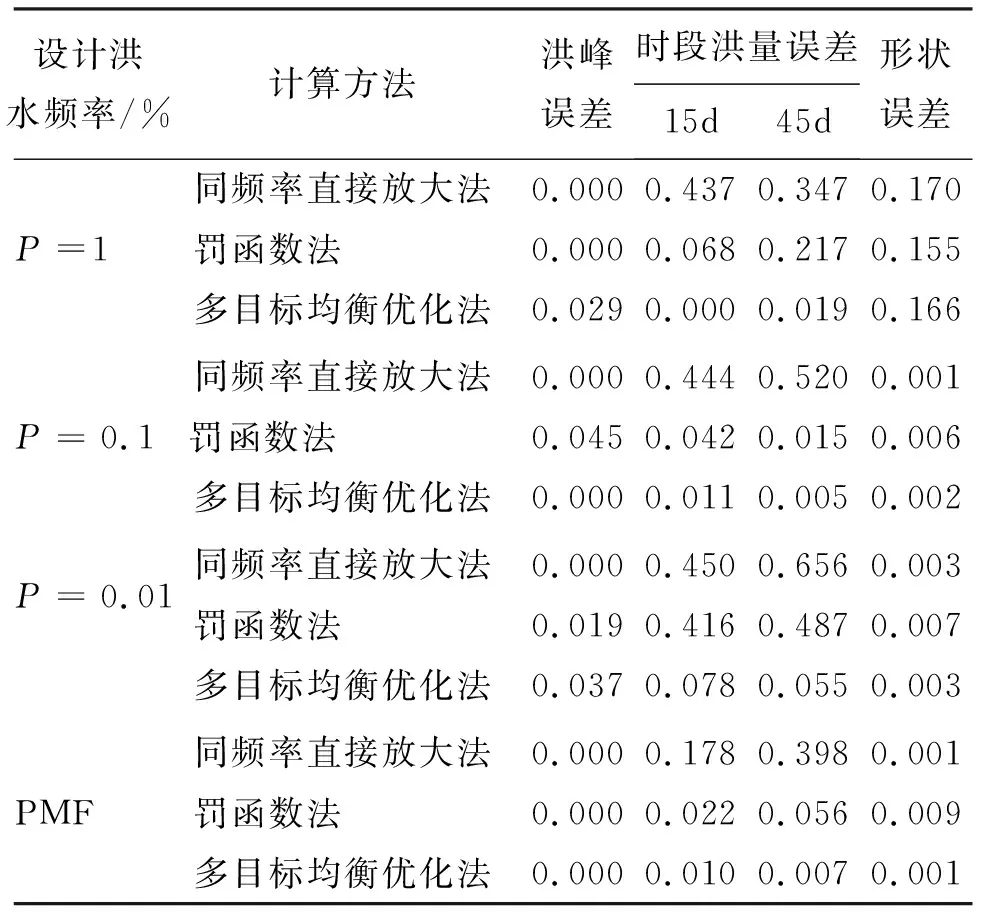
表2 刘家峡水库1964年各频率设计洪水不同计算方法推求误差 %

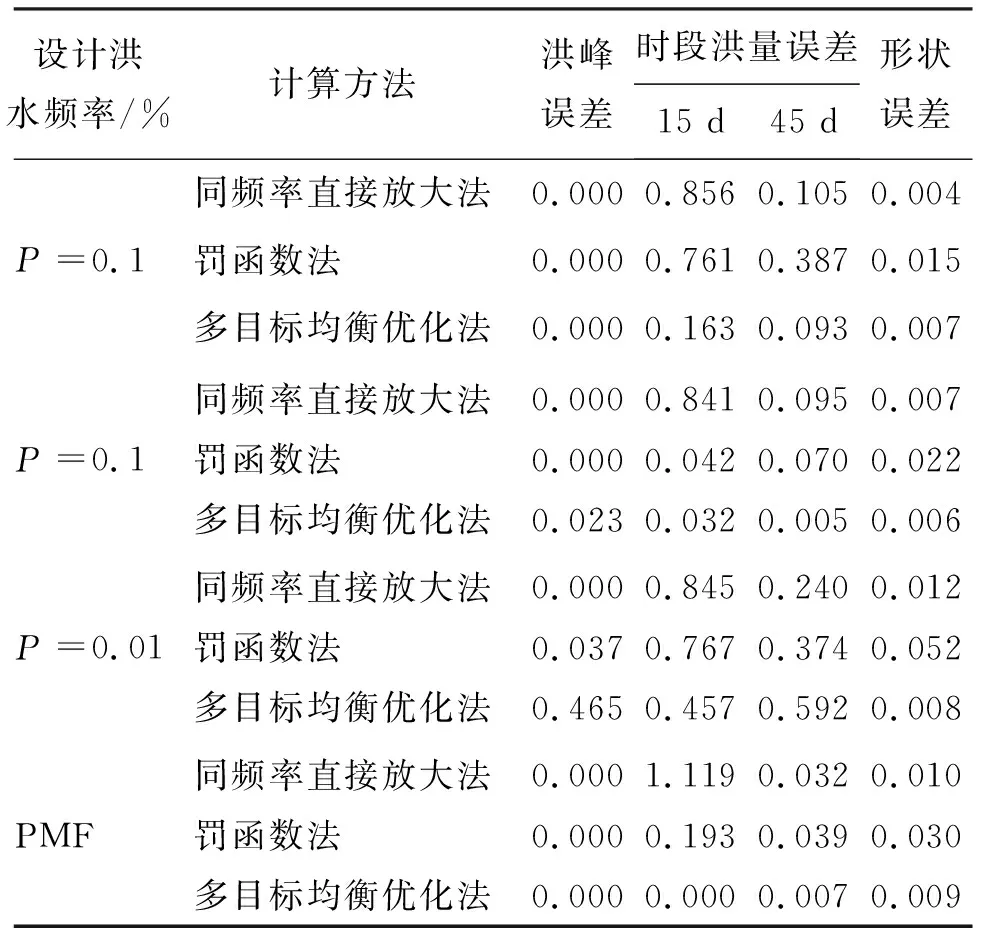
表3 刘家峡水库1967年各频率设计洪水不同计算方法推求误差 %

由表2和图4可知，在推求1964年设计洪水时，3种方法均有较优的表现，计算结果基本接近各频率下的设计值(洪水峰、量误差均小于1%)。但是，罚函数法所得设计洪水过程线与另外两种方法的结果差异明显，集中体现在形状误差上。在P=0.1%、0.01%及PMF(probable maximum flood)设计标准下，罚函数法所得的洪水过程线的形状误差均大于另外两种方法所得的形状误差。由表3和图5可知，在推求1967年设计洪水时，3种方法推求的洪水设计误差也基本相近。但是，基于罚函数法推求的设计洪水过程线变形较为严重，尤其是在设计频率P=0.01%下的形状误差最大。

采用2.4节构建的设计洪水推求方法的综合评价模型，对同频率直接放大法、罚函数法和多目标均衡优化法进行评价，评价结果如表4所示。由表4可知，设计洪水推求方法的优劣排序依次为：多目标均衡优化法>罚函数法>同频率直接放大法。结合表2和3可知，多目标均衡优化方法推求的设计洪水在峰、量、形方面均有较优的表现，而另两种方法往往只侧重于洪水设计误差的一两个方面，在综合评价中并不理想。因此，相比同频率直接放大法和罚函数法，多目标均衡优化法能够更好地满足设计洪水推求对洪水峰、量、形的要求。除此之外，多目标均衡优化法还可以根据实际需要对典型洪水自动放大，大大减小了计算过程的复杂程度。

表4 设计洪水3种推求方法的综合评价结果

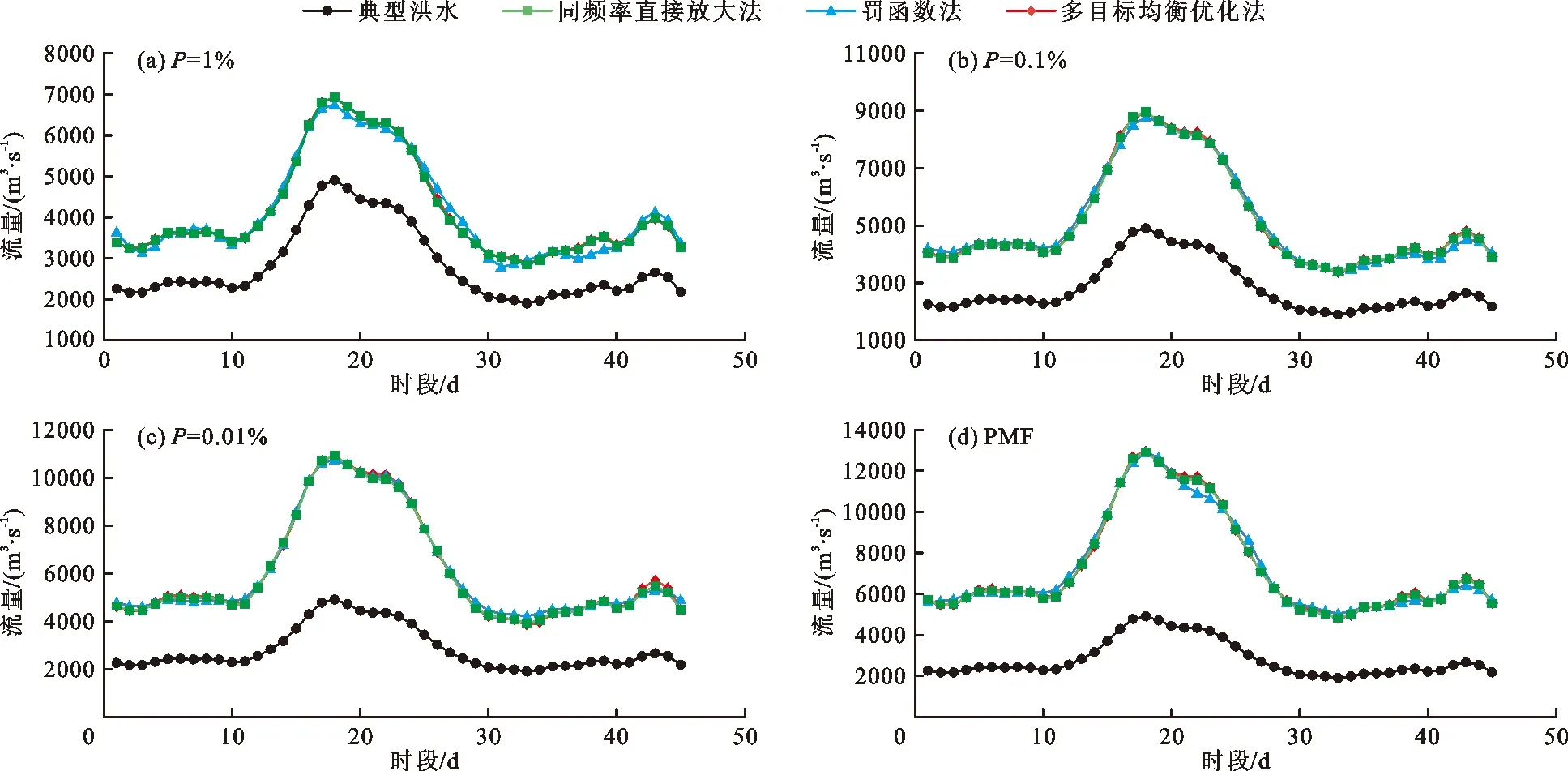
图4 刘家峡水库1964年典型洪水及各计算方法推求的不同频率设计洪水过程线

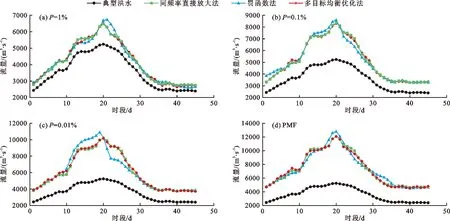
图5 刘家峡水库1967年典型洪水及各计算方法推求的不同频率设计洪水过程线

4 讨 论

洪水过程属于多特征量事件，受洪峰、洪量和过程线形状3方面因素的影响[3]。传统计算方法通常对特征量分别进行处理，没有综合考虑特征量之间的相关关系[5,24]。

本研究采用同频率直接放大法推求设计洪水所得的形状误差较小，而洪水峰、量设计值与相应特征值的偏差较大。

由此可见，采用同频率直接放大法推求设计洪水，能够较大程度保持典型洪水过程线形状，但会给洪水的峰、量设计带来较大的误差。

利用罚函数法推求设计洪水时，需要通过设置惩罚因子来控制洪水峰、量、形三者的误差[6-7]。在设计洪水推求中，需要经过多次试算来确定合适的惩罚因子。当惩罚因子设置较小时，难以满足洪水峰、量设计要求；当惩罚因子设置过大时，洪水过程线形状则变形明显。因此，采用罚函数法推求设计洪水，很难确定一个合适的惩罚因子，这也是本研究采用罚函数法推求设计洪水所得形状误差偏大的主要原因。

肖义等[3]建议可将表征洪水过程的多个特征量转化为1个特征量来分析计算，这与本研究构建误差向量的思路基本一致。本研究提出的多目标均衡优化法综合考虑了约束条件以及数值变化的稳定性，缓解了洪水峰、量约束与典型洪水过程线形状误差约束之间的矛盾，弥补了罚函数法的不足，且该方法无需设置惩罚因子，可基于误差向量直接求解，明显减少了模型的不确定性，在洪水的峰、量、形3方面均表现良好，在综合评价中表现最优。

本研究通过控制误差向量的均值和标准差之和最小化，来实现洪水设计误差的均衡优化。在优化计算中默认不同误差要素的均值和标准差具有相同的重要性，并未考虑不同权重设置对洪水设计结果的影响。事实上，均值和标准差的权重设置会影响误差向量的优化效果和均衡程度。具体而言，若均值的权重设置过大，则会导致误差向量元素存在较大差异，难以保证洪水峰、量、形的整体协调性；若标准差的权重设置过大，则会导致误差向量整体偏离设计值，不利于达到整体优化目标。因此，如何合理设置权重，协调均衡与优化间的关系，进而改善多目标均衡优化法的效果，为流域防洪规划设计提供科学依据，还有待进一步研究。

5 结 论

本研究将系统均衡优化思想用于解决设计洪水推求问题，基于设计洪水要素构建洪水设计误差指标向量，根据该误差向量建立均衡优化模型推求设计洪水，经实例分析得出以下结论：

(1)相比同频率直接放大法和罚函数法，多目标均衡优化法在洪水的峰、量、形3方面综合表现最优，所得设计洪水的峰、量、形误差均不超过0.6%，能够满足水利工程的设计标准。

(2)相比同频率直接放大法，多目标均衡优化法可自动放大典型洪水，无需手动修匀计算，减小了计算的复杂性；相比罚函数法，多目标均衡优化法无需设置惩罚因子，减少了计算的不确定性。