高山区雪堆储雪的实验和模拟计算

王 兴， 王飞腾， 任贾文， 秦大河

（1.中国科学院西北生态环境资源研究院冰冻圈科学国家重点实验室，甘肃兰州 730000； 2.中国科学院大学，北京 100049）

0 引言

储雪是指按照低环境影响和经济性原则，将雪储存起来以度过一年中温暖的季节［1-2］。随着人类历史的发展，储雪的应用目的不断发生变化。早期储雪被广泛应用于食品储存和房间制冷［3-4］，尤其是随着气候变暖［5］，对于建筑制冷的需求不断增加［6-7］；近年来，随着冰雪运动的发展，储雪对滑雪产业的作用越发重要［8-9］，能够增加雪场运营时间、降低投资成本和节能环保等。许多冬季雪上运动赛事都会提前进行储雪作业，尤其是近几十年，储雪成为雪上运动赛事规划必不可少的一部分，例如索契和平昌冬奥会都提前进行了储雪［10-11］。

目前最常见的储雪方法是将雪储存在地面上并覆盖绝热保温材料［12］。为了保证储雪结束时的用雪安全，需要对储雪融化量进行模拟，并指导储雪方案的设计。Olefs 等［9］在奥地利高海拔地区使用SNOWPACK 模型模拟了绝热保温层对积雪能量平衡的影响。Grünewald 等［1］发现SNOWPACK 模型在点尺度上可以很好地模拟雪堆的高度变化，但是对雪堆三维变化的模拟误差较大。Lintzén等［2］在瑞士使用稳态方法计算了由于地面温度、降雨和空气温度所导致雪堆融化的量。总的来说，目前储雪实验研究较少，主要在高纬度地区开展，缺乏中低纬度地区的储雪技术和经验；储雪材料的选择多依靠个人经验，缺乏理论指导；储雪结果关注质量变化，而忽视雪质的好坏；另外，国外在储雪技术方面对国内进行技术封锁。

储雪所用绝热保温结构的作用是减少由外界环境进入雪堆的热量。绝热保温结构的传热是一个复杂的非稳态过程，其温度场在不断变化，因此在计算绝热保温结构的传热量时需要使用非稳态的导热方法，常见的非稳态导热方法有反应系数法［13-15］、谐波反应法［14-15］、有限差分法［15-17］和有限元法［18-19］。谐波反应法的物理意义明显，不需要反复迭代运算，是国内计算室内空调冷负荷问题的主要方法［14］。外界气象条件具有不同时间尺度的变化特征，但从逐日来看，其大致以24 小时为周期发生变化。因此本文基于平均逐时气象数据，以24小时为周期，使用谐波反应法计算雪堆的融化量并分析储雪过程中绝热保温结构的传热特征。

1 方案与数据

1.1 实验地点

本次储雪实验于2019 年5 月25 日开始，地点位于阿勒泰山南麓，萨吾尔山北部，距离木斯岛冰川北侧6 km，新疆阿勒泰地区吉木乃县正南39 km处的高山区气象综合观测场附近（47° 08′N，85°35′E，海拔2 915 m）（图1）。该地区属于中国三大稳定积雪区之一，冬季降雪丰富，为本次实验提供了充足的物质基础。其降水主要受西风气流的控制，其次受北冰洋冷湿气流的影响，属于典型的北温带大陆性寒冷气候［20-21］。实验地点所在的阿勒泰地区滑雪历史悠久，滑雪产业发达，到2013 年阿勒泰地区滑雪场已达30多家［22］。

图1 储雪位置Fig.1 Location of snow storage

1.2 气象及雪堆数据

气象数据由高山区气象综合观测场的自动气象站提供，模拟所使用的气象要素包括气温、入射和出射的短波辐射。数据采集器（CR1000）每半小时存储一次气象数据。雪堆的初始密度及含水率数据使用SLF积雪传感器进行测量。雪堆质量变化数据使用5个压力传感器为一组进行测量。由于传感器技术故障，气象数据于2019 年6 月22 日开始获取至8月25日结束。具体传感器类型和参数见表1。

表1 传感器类型和参数Table 1 Sensor information and technical specifications

1.3 实验方案

储雪实验自2017 年就已经在河北延庆石京龙滑雪场开展，其主储雪堆上表面绝热保温结构为表层土工织布（0.5 cm 厚度）+多层铝箔PE 保温层（0.5～3.0 cm 厚度）+底部土工织布的三元结构。2018 年又在河北崇礼万龙滑雪场开展了四种储雪堆覆盖方案的对比研究实验［23］。本研究基于前期的经验，选择了较优的储雪方案，在吉木乃县开展实验。

本次实验设计有两个雪堆（图2），其形状为正四棱锥，底面边长为2.8 m，棱锥的高为1.5 m，棱锥每个面的坡度为49°，四个面的朝向分别为南、西、北和东。雪堆1 上表面覆盖绝热保温材料，雪堆2上表面则不覆盖任何材料。为了评价雪堆上表面覆盖材料的绝热保温效果，两个雪堆底部均置于压力传感器之上并与地面分离，其分别由铁架、铁皮、挤塑聚苯乙烯泡沫塑料保温板和铝箔反射膜组成。针对以往储雪实验中使用硬性绝热保温材料所带来的施工困难，以及与雪堆贴合性差、易滑落等问题［24］，本次实验雪堆1 上表面使用玻璃棉毡软性材料。高山地区，太阳辐射是积雪融化的重要能量来源［8，25］，因此在玻璃棉外侧覆盖铝箔反射膜以降低雪堆太阳辐射得热量。铝箔反射膜外覆遮阳网，起到固定内侧绝热保温材料和降低内侧太阳辐射的作用。各材料具体的参数见表2。

图2 高山区气象观测场附近的储雪实验Fig.2 Snow storage near the meteorological observation site in alpine region

表2 材料的物理特征Table 2 Physical characteristics of materials in this study

2 方法

2.1 模拟方案

融雪期，自然状态下的积雪与周围环境的热量交换包括雪面的净辐射通量、感热通量、潜热通量、地热通量和雨水热通量［26-27］。储雪所用绝热保温结构的特性直接或间接影响着雪堆的能量平衡。绝热保温结构的辐射特性影响雪面的净辐射通量；绝热保温结构的总传热系数影响雪面的感热通量和地热通量；绝热保温结构的渗透率影响雪面的潜热通量和雨水热通量。雪堆上部热量和水分的传输过程如图3所示。影响雪堆融化速率的外界气象要素主要有两项，太阳辐射和外界空气温度［28-29］。雪堆融化过程中，外界环境通过绝热保温结构向内部的传热可以分为三个过程：绝热保温结构外表面的吸热过程，绝热保温结构的导热过程和绝热保温结构内表面的放热过程［30］。外界环境通过绝热保温结构向雪堆传递热量主要通过覆盖层的热传导。雪堆吸热后，冷储减少，雪堆温度升高。本实验因为雪堆完成覆盖一段时间后，才获得各种有效观测数据，且模拟初期雪堆质量就已经开始减少，亦即雪堆内部已经有融化且通过融水流失使雪堆质量减少，所以假定雪堆各层和内部空气层的温度均为0 ℃，从而使绝热保温结构的传热量全部用于雪堆的融化。当雪堆温度升高为0 ℃时，雪堆开始融化，大部分融水自上而下进行水分的迁移，但有时间滞后，而且一部分融水被雪堆截留。融水从雪堆中流出会引起雪堆质量的变化，本实验中假定融水能够全部流出雪堆。

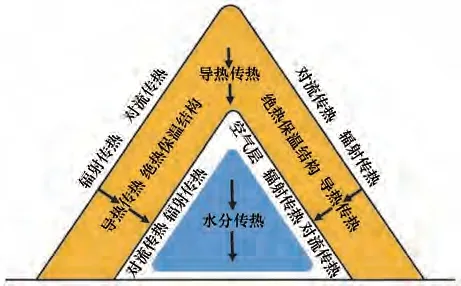
图3 雪堆上部热量和水分的传输Fig.3 Transportation of heat and water on the upper part of the snowpack

2.2 斜面太阳辐射总量逐时计算模型

斜面太阳辐射总量I（W·m-2）由三部分组成［15］，直接辐射量IDβ（W·m-2），散射辐射量Idβ（W·m-2），地面反射辐射量Irβ（W·m-2）。

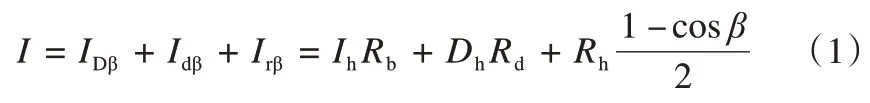
式中：Ih为水平面的直接辐射量（W·m-2）；Rb为直接辐射转换系数；Dh为水平面的散射辐射量（W·m-2）；Rd为散射辐射转换系数；Rh为地面反射的辐射量（W·m-2）；β为斜面的倾角。

直接辐射转换系数Rb为：

式中：θ为斜面太阳入射角（°）；z为太阳天顶角（°）。

散射辐射转换系数Rd的计算采用各向异性模型［31］：

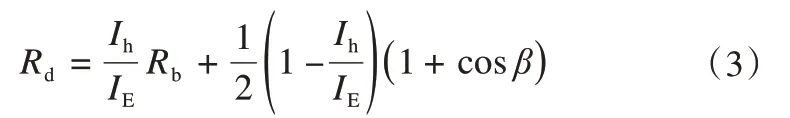
式中：IE为水平面天文辐射量（W·m-2）。

2.3 非稳态热传导模型

谐波反应法是建立在绝热保温结构导热方程经典求解的基础上，将外界综合空气温度视为以24小时为周期的不规则周期函数（图4），使用傅立叶级数对外界综合温度进行表达，并引入衰减和延迟的概念。谐波反应法计算绝热保温结构的传热量分为两部分，一部分为外界平均综合温度与绝热保温结构内部温度之差所引起的传热量；另一部分是由于外界综合温度相对于平均温度的波动所引起的绝热保温结构内表面波动而产生的附加传热量。

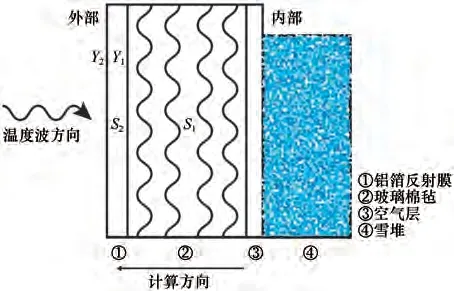
图4 雪堆1上表面各材料层表面蓄热系数和蓄热系数的计算Fig.4 Calculation of surface heat storage coefficient and heat storage coefficient of each material layer on the upper surface of Snowpack 1

热量在固体中的传播服从傅里叶基本导热微分方程。一维无内热源非稳态导热微分方程为［32］：

式中：a为热扩散率。

外界综合空气温度Te（℃）可表述为［30］：

式中：Tair为外界空气温度（℃）；ρ为铝箔反射膜的吸收率（0.2）；τ为遮阳网的遮阳率（0.8）；αe为绝热保温结构的外表面换热系数，取其工程上的计算数值为23.26 W·m-2·K-1［33］。

外界综合空气温度Te展开为傅里叶级数的表达式为［14］：

通过绝热保温结构的导热量计算公式为［14］：

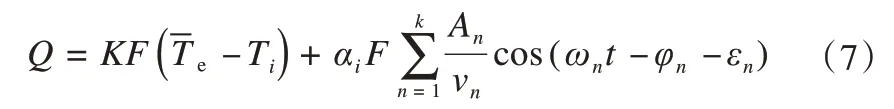
式中：K为绝热保温结构总传热系数（W·m-2·K-1）；F为绝热保温结构的面积（m2）；αi为绝热保温结构的内表面换热系数，取其在工程应用上的数值为7.5 W·m-2·K-1［34］；Ti为绝热保温结构内部空气层的温度（0 ℃），vn和εn分别为绝热保温结构的衰减倍数和延迟时间（弧度，rad）。

雪堆的融化量计算公式为：

式中：G为雪堆融化量（kg）；L为雪的融化潜热（MJ·kg-1）。

3 结果

3.1 气象数据

高山区综合观测场中的自动气象站观测结果显示，2019年6月22日至8月25日的平均气温为7.5 ℃，逐日平均气温和气温日较差变化均较大，其范围分别为1.2～13.4 ℃和1.8～10.8 ℃，原因可能与高海拔山区地带大气逆辐射的增温效果较弱和山区小气候复杂多变有关。水平面太阳辐射总量和地面反射辐射量的平均值分别为250.9 W·m-2和33.5 W·m-2。2019 年6 月22 日至8 月25 日，水平面太阳辐射总量为1 408.9 MJ·m-2（表3），地面反射的太阳辐射量为188.2 MJ·m-2。模拟期间（2019年6月22日至8月25日）所需要的逐时气象数据见图5。

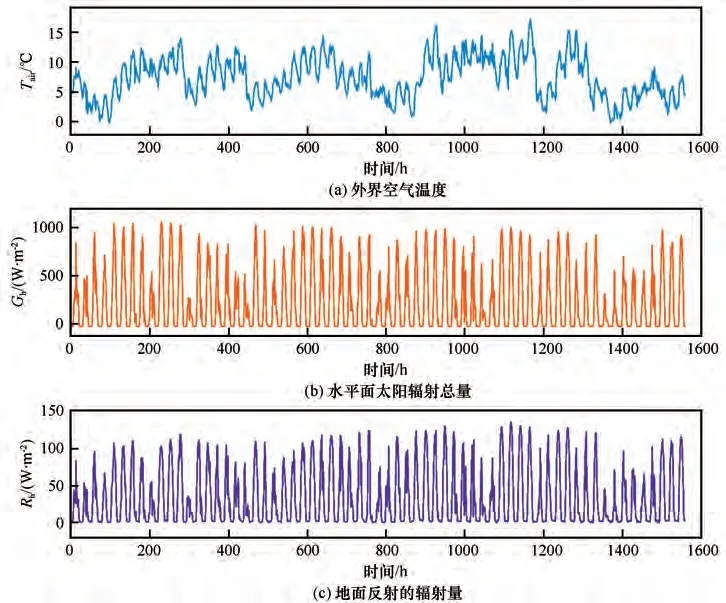
图5 逐时气象数据Fig.5 Hourly meteorological data［external air temperature（a），global solar radiation on the horizontal surface（b），reflected radiation on the ground（c）］

表3 太阳辐射总量Table 3 The global solar radiation

3.2 模拟结果与分析

3.2.1 各朝向斜面太阳辐射总量

通过斜面太阳辐射总量逐时模型计算得到雪堆南（S）、西（W）、北（N）和东（E）四个不同朝向斜面的太阳辐射总量（直接辐射量、散射辐射量、地面反射的辐射量）的逐时值（图6）。模拟结果显示，雪堆各朝向斜面太阳辐射总量具有很好的周期性变化特征，可以发现各朝向斜面的辐射变化规律与地球绕太阳的运行规律相对应［图6（a）、6（b）、6（c）］。北向斜面无太阳直接辐射［图6（b）］，北向斜面的太阳辐射总量仅由散射辐射量和地面反射辐射量两部分组成。

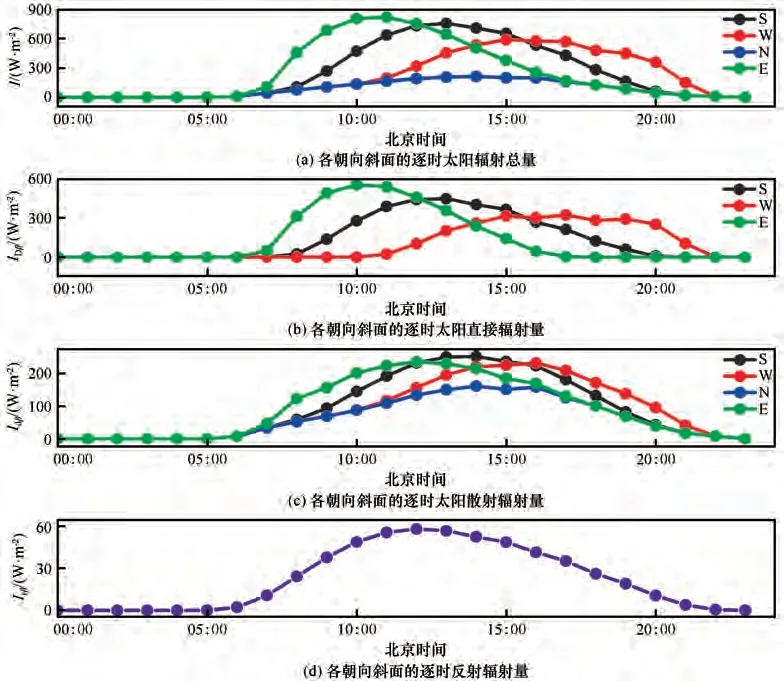
图6 各朝向斜面平均日太阳辐射量的逐时值（S：南向斜面；W：西向斜面；N：北向斜面；E：东向斜面）Fig.6 Hourly average daily solar radiation of each inclined plane（S：south-facing surface tilted；W：west-facing surface tilted；N：north-facing surface tilted；E：east-facing surface tilted；B：bottom surface）［hourly global solar radiation of each inclined plane（a），hourly direct solar radiation of each inclined plane（b），hourly diffuse solar radiation of each inclined plane（c），hourly reflected radiation of each inclined plane（d）］

实验期间雪堆各朝向斜面的太阳辐射总量都未超过水平面的太阳辐射总量（表3）。斜面太阳辐射总量最大的方位角受地区纬度、气象条件［35］和日期的影响，在本实验中，四个朝向斜面以东向斜面的太阳辐射总量最多，南向斜面的太阳辐射总量与东向斜面相接近。从各斜面太阳辐射总量的组成比例来看，南、西和东向斜面太阳直接辐射总量占比最大，分别占太阳总辐射量的53.7%、48.7% 和54.3%。北向斜面散射辐射量的占比最大，达到73.5%。雪堆四个朝向斜面中地面反射辐射量的占比最小。

3.2.2 外界综合空气温度

外界综合空气温度的大小是由外界空气温度和太阳辐射共同决定的，各朝向斜面平均日外界逐时综合空气温度的计算结果见表4。00：00—06：00和22：00—23：00（北京时间，下同）各朝向斜面的太阳辐射总量为0，因此这两个时间段的各斜面综合空气温度相等，并在06：00 达到最低值。受太阳辐射的影响，南、西、北和东向斜面外界综合空气温度有不同幅度的提升，其外界平均综合空气温度分别为7.9 ℃、7.8 ℃、7.6 ℃和7.9 ℃（外界平均空气温度为7.5 ℃）。由于外界综合空气温度的变化规律不是一个完美的谐波曲线，同时为了提高傅里叶级数拟合的精度，因此在本文中将四个朝向斜面的外界综合空气温度以及外界空气温度展开为12 阶傅里叶级数来进行叠加拟合（图7），拟合后的温度与原温度之间的差值小于0.01 ℃。

图7 各朝向斜面外界综合空气温度傅里叶级数拟合（A：外界空气温度；S：南向斜面；W：西向斜面；N：北向斜面；E：东向斜面）Fig.7 Fourier series fitting of the solar and external air temperature in each inclined plane（A：external air temperature；S：south-facing surface tilted；W：west-facing surface tilted；N：north-facing surface tilted；E：east-facing surface tilted）

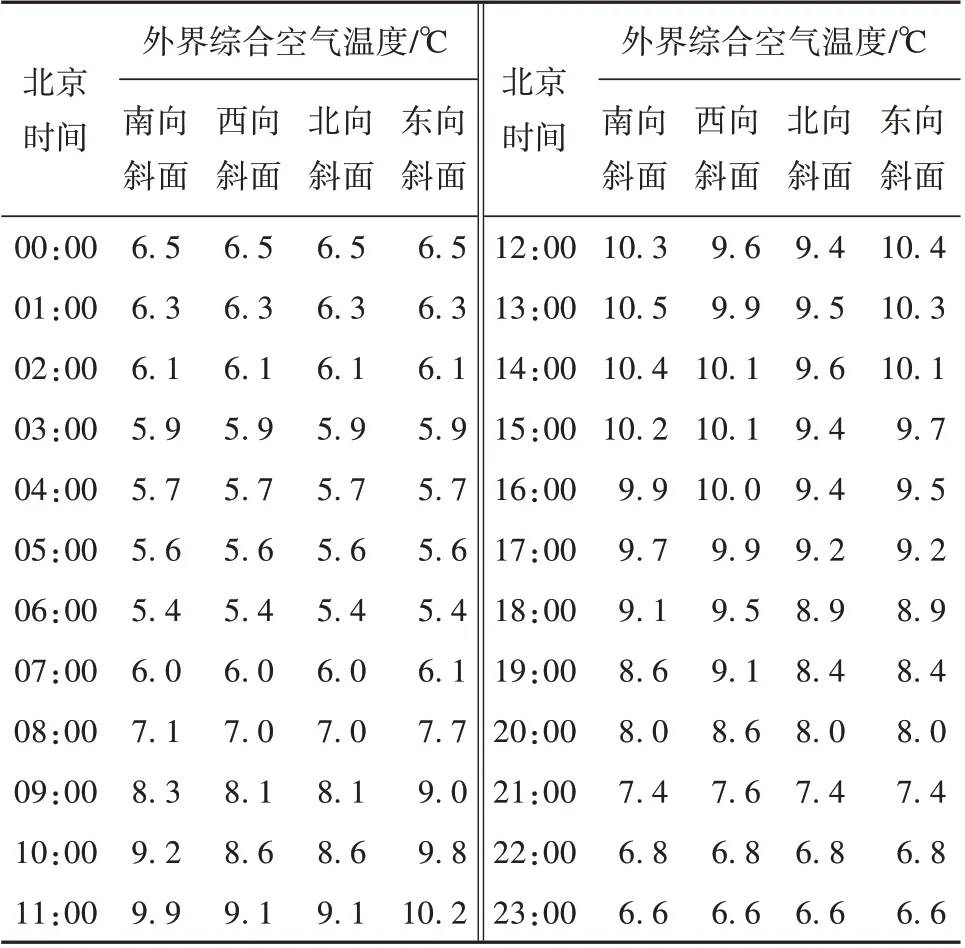
表4 各朝向斜面平均日外界逐时综合空气温度Table 4 Hourly average daily solar and external air temperature of each inclined plane

3.2.3 逐时传热量和雪堆融化量

外界环境通过绝热保温结构的热量可以分为两个部分，雪堆1上表面绝热保温结构的导热量（第一部分）和雪堆底部绝热保温结构的导热量（第二部分）。非稳态方法计算第一部分使用的外界环境参数为各朝向斜面的外界综合空气温度，第二部分使用的外界环境参数为外界空气温度。雪堆上表面绝热保温结构各朝向斜面的面积均相等，为2.8 m2，底部面积为7.8 m2。图8显示有两个时间段雪堆底部绝热保温结构的导热量大于各朝向斜面的导热量，分别为00：00—07：00 和19：00—23：00。由于雪堆底部和上表面绝热保温结构的延迟时间不同，导致第一部分与第二部分逐时曲线的波谷位置不同（图8）。绝热保温结构南、西、北、东朝向斜面逐时导热量分别在14：00、15：00、14：00 和13：00达到峰值，绝热保温结构底部逐时导热量在18：00达到峰值。实验期间外界环境通过绝热保温结构的热量中第一部分占比为79.7%，第二部分占比为20.3%，表明通过绝热保温结构的热量中第一部分是影响雪堆融化量的主要因素，这与其他储雪实验结果一致［2］，经分析发现，原因主要有两个：雪堆上表面绝热保温结构的面积大于底部的面积；雪堆上表面绝热保温结构的边界条件比底部更有利于增加传热量。

图8 绝热保温结构的逐时导热量（S：南向斜面；W：西向斜面；N：北向斜面；E：东向斜面；B：底部）Fig.8 Hourly conduction of thermal insulation structure（S：south-facing surface tilted；W：west-facing surface tilted；N：north-facing surface tilted；E：east-facing surface tilted；B：bottom surface）

储雪实验于2019 年5 月25 日开始，雪堆1 初始质量为2 115.0 kg，雪堆2的初始质量为1 812.0 kg，雪堆2 在储雪开始15 天后于6 月8 日全部融化（图9）。

图9 雪堆的状态Fig.9 The state of the snowpack

本次实验中，上表面覆盖绝热保温材料的雪堆1 平均融化量为18 kg·d-1（相当于初始质量的0.85%），未覆盖绝热保温材料的雪堆2 平均融化量为120.8 kg·d-1（相当于初始质量的6.67%）。由于传感器技术故障，模拟从6 月22 日开始，模拟期间雪堆1 质量减少了1 438.0 kg，对应的模拟值为1 520.8 kg（6月22日至8月25日）。

4 讨论

非稳态导热问题的求解，本质上就是在定解条件下求解导热微分方程［36］。谐波反应法将边界条件的离散数据转化为傅里叶级数，引入衰减倍数和延迟时间参数，物理意义明确，但该方法受限于周期性边界假设条件的限制，只适用于计算平均日导热微分方程，而无法计算全年任意时间的导热微分方程。在本实验中，使用谐波反应法计算平均日绝热保温结构的传热量，可为分析储雪所用绝热保温结构的传热特性提供重要的参考。储雪过程中能量和物质的传输是一个受多要素综合影响的复杂过程，具体的模拟和量化的研究较少［1-2，37-38］。通过对模拟和观测结果的比较证明，谐波反应法可以为建立外界空气温度、太阳辐射、绝热保温结构的热学性质和雪堆融化量的关系提供科学依据，对提前确定储雪量具有重要的参考价值，因此在储雪工程上求解平均日一维非稳态导热问题时，可以使用谐波反应法。

4.1 雪堆融化速率敏感性分析

储雪期间，雪堆1 的平均融化量为18.0 kg·d-1（相当于初始质量的0.85%），雪堆2 的平均融化量为120.8 kg·d-1（相当于初始质量的6.67%），说明在本次实验中雪堆1上表面所使用的覆盖方案可有效减少外界气象环境对雪堆融化的影响。雪堆的融化速率主要受外界气象条件、绝热保温结构的特性和雪堆几何特征的影响［39］。储雪地点可以选择在遮阳、低风速的位置，以降低外界气象条件对雪堆融化的影响。各材料层的热阻是绝热保温结构热阻的主要贡献者，因此在符合经济性原则的基础上可以选择导热系数较小的材料或增加各材料层的厚度来减少雪堆融化的速率。当外界气象条件一定时，相同体积下，越小的雪堆表面积意味着越少的热量进入雪堆，即雪堆表面积与体积的比例越小，雪堆的融化速率越小。

4.2 误差分析

模拟计算雪堆融化量的误差主要包括以下五部分。

（1）融水全部流出雪堆。雪堆的融化外流过程可以分为两个阶段［40］：雪堆升温为0 ℃时，雪堆表面开始融化并渗入雪堆内部的停蓄阶段；当雪堆内部的液态水达到最大持水量时，融水才能从雪堆中流出的外流阶段。实际融化的雪水并没有全部流出雪堆，有一部分被雪堆截留，保存在雪堆内部。雪堆质量变化反映的是流出雪堆的那部分融水损失。融水的外流时刻和雪堆截留的融水量主要与雪堆的融化速率、最大持水量、雪堆的高度和体积有关。融化速率主要受能量输入大小的影响。雪堆最大持水量的大小主要受雪堆密度的影响［28-29］，储雪过程中，由于压力和变质作用等，导致雪堆密度增大，持水能力降低，促进了融水的外流。雪堆高度的下降将导致融水在雪堆中迁移路径减小，同时高度和体积的减少，使得雪堆容纳融水的空间变小，促进了融水的外流。因此雪堆质量的变化并不能完全代表雪堆的融化量，此误差是由截留在雪堆内部的融水量造成的。雪堆截留水量对融化量模拟的影响在储雪初期较大，导致模拟的雪堆融化量大于雪堆质量的变化。

（2）非稳态方法计算传热量所用绝热保温结构的几何参数。模拟中所使用绝热保温结构的几何参数不随时间的变化而变化，但实际过程中随着雪堆的融化，绝热保温结构的几何参数必然会发生相应变化，此误差将导致模拟的雪堆融化量大于实际的融化量，但在实际的储雪工程中对提前确定储雪量是相对安全的。

（3）雪堆太阳辐射热量。铝箔反射膜与遮阳网之间存在一系列的反射和透射过程［41］，因此在计算雪堆融化量的过程中可能严重低估了太阳辐射对于雪堆融化的影响。

（4）模拟计算所用各材料的基础参数均是通过查表获得，可能与材料实际的参数不符，导致计算结果存在偏差，同时模拟计算结果仅以雪堆质量的变化作为验证标准，缺少雪堆表面热通量等实测数据，使得模拟计算的绝热保温结构的传热量与实际值的偏差未知。

（5）没有考虑长波辐射项。涉及夏季绝热保温领域的研究中，长波辐射项对绝热保温结构外表面的热作用通常被忽略，这是因为在夏季忽略此项对于计算结果是相对安全的［15］，此误差将导致模拟的雪堆融化量大于实际的融化量。

5 结论

通过开展储雪实验，以及定量、定性分析，结果表明雪堆1的平均融化量为18.0 kg·d-1（相当于初始质量的0.85%），雪堆2的平均融化量为120.8 kg·d-1（相当于初始质量的6.67%）。雪堆1 上表面绝热保温结构可以有效减少雪堆融化量，证明在新疆阿勒泰地区进行人工储雪是可行的。使用本实验的储雪覆盖方案（反射层和保温层）可以有效减缓雪堆的融化，为今后阿勒泰地区的储雪工程提供技术和方案等方面的借鉴。通过对外界综合空气温度的傅里叶级数描述发现，对于不规则的谐波变化曲线，使用高阶傅里叶级数叠加拟合可以完美描述这一曲线变化。虽然本文对雪堆融化量的计算是一个比较粗糙的过程，但模拟结果与观测值的结果比较仍可以证明，使用数学方法计算雪堆的融化量是可行的。谐波反应法可以为建立外界空气温度、太阳辐射、绝热保温结构的热学性质和雪堆融化量的关系提供科学依据。雪堆覆盖的绝热保温结构可以用反射率、总传热系数、衰减度和延迟时间来进行评价。

虽然雪堆融化量的模拟可以较好地反映雪堆质量的变化，但许多物理过程都未考虑，尤其是未考虑储雪过程中雪堆形状和截留水量的变化，使得模拟结果与实际雪堆融化量的关系仍存在不确定性。下一步储雪实验研究可使用地面激光扫描仪定期获取雪堆随时间变化的高精度几何数据，并在雪堆表面和内部分别布设热通量和含水量传感器，从而进一步验证模拟结果与实际融化量的关系。