VIC-CAS导热率和未冻水算法改进及其对多年冻土水热过程模拟的实验研究

李 飞， 郭佳锴， 张世强

（1.西北大学陕西省地表系统与环境承载力重点实验室，陕西西安 710127； 2.西北大学城市与环境学院，陕西西安 710127）

0 引言

据统计，多年冻土约占北半球陆地面积的24%［1］，我国是世界第三冻土大国，多年冻土主要分布在青藏高原、东北北部山区和西北高山区。冻土作为一类特殊的岩土，与外界能量的交换会改变自身的热力学和水力学性质，因此在冻融阶段的物理过程极其复杂。活动层内部土壤的水热迁移在地气交互和能水平衡中起着重要作用［2］，影响冰冻圈生态环境［3］和流域水文过程［4］。

青藏高原多年冻土总面积约1.06×106km2，约占高原总面积的40%［5］。高海拔和复杂地形使青藏高原对全球气候变化极为敏感，并通过能水交换与大气循环作用反馈到全球气候变化进程中［6］，是全球气候的放大镜和调节器［7］，而作为高原典型下垫面类型的多年冻土是影响全球气候变化的关键因子。近几十年，在全球气候变暖的背景下，青藏高原的多年冻土呈现退化的趋势，主要表现为多年冻土年平均地温升高，活动层厚度加深，冻土下限海拔上升，多年冻土区面积减小［8-11］。已有研究表明，冻土退化使高原植被退化，加速了高原草地荒漠化和盐渍化的速度［3，12］，同时流域内夏季径流减少、冬季径流增加、年内径流过程变缓，变化强度与流域多年冻土覆盖率有关［13-16］，部分地区地下水储量增加［17］等。研究冻土区土壤的水热变化可以为未来气候模式下更准确预估冻土的变化趋势，为当地生态环境保护、水资源利用、下游社会经济发展提供重要决策依据。

在寒区陆面过程研究工作中，土壤内部水热过程的准确描述一直是难点之一。国内外科学家基于不同的算法与需求开发大量陆面过程模型，其中代表性的有SHAW（Simultaneous Heat and Water Model）［18］、CoupModel（Coupled Heat and Mass Transfer Model for Soil-Plant-Atmosphere System）［19］和VIC-3L（Variable Infiltration Capacity-3 Layer Model）［20］等，这些模型通过耦合冻土模块，实现了冻土水热过程的模拟。

陆面模型为了便于描述陆面过程，通常将复杂的陆面过程参数化，在影响冻土水热模拟的参数中，土壤导热率影响土壤和大气的能量交换以及土壤内部间的能量传递，对土壤温度模拟的影响很大［21］。很早就有国外学者对土壤热导率进行了相关研究［22-23］，Johansen［24］在Kersten［22］研究的基础上于1975年首次提出了归一化导热系数的概念，建立了一个模拟非饱和土壤热导率的半理论模型，适用性较广。Côté 等［25］、陆森等［26］在Johansen［24］算法的基础上对土壤热导率进一步改进提高了模拟精度，扩大了适用范围。Yang 等［27］结合全球土壤实测资料改进了Johansen［24］算法，提高了土壤在冻结状态下的导热 系数精 度。 Bao 等［28］在EBM（Eaphy-Based Model）中借鉴了Yang 等［27］的成果，并嵌入了冰的导热算法［29］，在祁连山多年冻土区水热模拟方面取得了不错的进展。在国内冻土导热系数的研究中，李韧等［30］基于野外实测数据推导出适用于青藏高原北部的计算公式。而罗斯琼等［31］、王愚等［32］在Farouki［33］、Johansen［24］、Côté等［25］参数化方案的基础上发展了适用于青藏高原中部的导热系数方案并取得了较好的效果。刘为民等［34］基于土体成分和特性等因素，任小鹏等［35］考虑了土壤水分的相变和岩土的特点建立了各自的导热计算模型，但都存在局限性。未冻水含量对土壤热力学参数和物理性质有着重要意义［36-37］，影响冻融过程中水分的迁移［38］。未冻水的计算模型包括经验模型和理论模型，部分模型如GIPL2（Geophysical Institute Permafrost Lab 2.0）［39］采用徐斅祖等［37］、Lovell［40］基于实验数据提出的关于土壤温度的未冻水经验公式。VIC-3L、CLM（Community Land Model）［41］、FEFLOW（Finite Element Subsur-face Flow System）［42］等模型采用了在不同的冻融方案下的未冻水计算公式［43-45］。张世强等［46-47］、Pan 等［48］和郭林茂等［49］分别利用不同的陆面模型在青藏高原展开水热模拟研究，对各模型未冻水方案在水热模拟方面的适用性有着很好的参考作用。

已有研究者在青藏高原多年冻土区探究陆面模型中参数化方案对水热模拟的影响，Hu等［50］在唐古拉站和西大滩站对比了Johansen［24］、Farouki［33］和罗斯琼等［31］三种热导率方案，发现罗斯琼等［31］的方案在未冻结土壤中表现最好，而Johansen［24］方案在冻结土壤中表现最好。Yang 等［51］在CLM 5.0［52］的基础上，在6 种典型的植被下垫面下比较了9 种标准化导热率方案对土壤热状态的模拟结果，结果表明选取的所有导热率方案的计算值都偏高并低估了冻结期的土壤温度，在这些方案中Johansen［24］方案及其派生方案在导热率的数值估算以及模拟土壤温度方面明显更优，其中Balland等［53］的导热率方案在不同类型土壤的综合适用性最好。刘火霖等［54］在那曲站评估了Noah-MP（The Community Noah Land Surface Model with Multiparameterization Options）陆面模型［55］下Niu 等［44］和Koren 等［56］两种未冻水参数化方案，结果表明未冻水方案对土壤湿度模拟的影响明显大于土壤温度，未冻水方案的差异显著影响冻融期土壤水分含量的变化。Hu等［57］基于土壤温度、土壤颗粒比表面积、水的类型和土壤水分曲线建立的未冻水计算公式，归纳并总结了共34种未冻水方案，并根据实地数据进行了评估，结果表明经验公式可用于计算未冻水含量，而物理模型具有更高的精度，但更为复杂，难以在实际情况中应用。在这些方案中，van Genuchten［58］、Kozlowski［59］、Zhang等［60］的方案表现较好。

本研究在VIC-CAS 模型的基础上，综合比较了众多研究者在青藏高原水热模拟的结果，分别用EBM 导热率算法和CLM 5.0 未冻水算法替换原模型相应算法，利用长江源区的沱沱河站点观测资料进行为期一年的单点模拟试验，分析比较了不同算法下土壤冻融过程中温度和湿度的模拟效果，并针对模拟结果中存在的问题进行分析，为后续的模型改进提供支撑。

1 研究区概况与数据来源

沱沱河观测站（92°37′ E，33°57′ N）位于长江源的多年冻土连续区［61］，海拔4 533.1 m，地势平缓，气候干燥寒冷。地属高寒草甸地带，植被稀疏，植被覆盖度低。根据1997—1998年的观测，沱沱河站点的年平均气温达-3.7 ℃，最低气温为-32.9 ℃，最高气温为24.3 ℃。流域内降水较少，年降水量在300 mm 左右，降水集中在6—9 月，约占年降水量的85%，并在9月份降水量达到峰值。

本文观测数据来自“全球能水平衡试验-青藏高原亚洲季风试验”（Game-Tibet）项目1994—1999年的观测期内长江源区沱沱河站点的观测资料。观测数据来自土壤温度和湿度观测系统（SMTMS）收集的土壤温、湿度数据。由于受限于当地的气候条件和仪器损耗等客观因素，观测数据时间序列不连贯且部分时段数据误差较大，因此选择1997 年7月1 日至1998 年9 月29 日超过一年的观测数据，时间分辨率为1 h。

2 实验方法

2.1 VIC-CAS模型

VIC-CAS 由赵求东等［62］在VIC-3L 的基础上耦合冰川模块构成。VIC-CAS 模型以能量平衡和水量平衡为基础，在垂直方向上形成大气-植被-土壤的陆面模式，在单个格网上考虑植被、降雨、土壤、积雪等综合因素，输出单个格网的各模拟分量，并可通过汇流模型对流域内产流进行汇总。

模型的输入数据主要包括气象驱动数据、土壤参数数据、植被参数库和植被覆盖数据。模型的气象驱动数据包括气象站观测的逐时气温、风速、气压等和日降水资料作为模型的气象驱动数据输入。土壤参数数据来自国际地圈生物圈计划（IGBP）的全球土地覆盖特征数据集（GLCC）并参考了美国农业部土壤质地分类依据（USDA）和Cosby 等［63］的成果；植被参数库来自于GLCC 的亚洲青藏高原植被库，部分参数参考了高原其他地区的研究资料［64-65］；植被分布来源于美国马里兰大学发布的全球陆面覆盖类型数据集（UMD）。

2.2 导热率算法

影响土壤导热率数值的因素有很多，如土壤孔隙度、粒径、饱和度、温度［44，66-68］等。在对土壤导热率的众多算法中，VIC-CAS 模型中导热率选择应用最为广泛的Johansen［24］算法，导热率K可表示为：

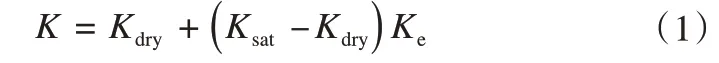
式中：Kdry为干土导热率，只与土壤块体密度ρd有关，可表示为：

Ksat为饱和土壤导热率，主要由土壤基质、水、冰的导热率及孔隙度决定，可表示为：

式中：T和Tf分别为土壤温度和冰点温度；n为土壤孔隙度；Ks为土壤基质导热率；Kliq为水的导热率，取值0.6 W·m-1·K-1；θliq为土壤液态水含量；Kice为冰的导热率，取值2.29 W·m-1·K-1。

Ke是Kersten 系数，是关于土壤饱和度Sr的函数，可表示为：

式中：Sr与土壤中液态水含量θliq、含冰量θice以及孔隙度n有关，可表示为：

本研究选择EBM导热率算法替换原模型算法，EBM中导热率K表示为：

式中：Kdry为干土导热率，计算公式与式（2）相同。

Kwet［27］为湿土导热率，可表示为：

式中：w为土壤有效湿度，与土壤中液态水含量θliq和土壤饱和含水量θsat有关，可表示为：

Ki为土壤中冰的总导热率，与土壤含冰量有关，可表示为：

2.3 未冻水算法

VIC-CAS模型的最大未冻水含量公式［43］如下：

式中：θsat为土壤饱和含水量；g为重力加速度，取值9.81 m·s-2；φc为进气值；T为土壤温度；Lf为相变潜热，取值3.36×105J·kg-1。Bp为土壤孔隙形状参数，是关于水力传导层指数函数，可表示为：

本研究选择CLM 5.0 中的未冻水算法代替原模型算法，公式如下：

式中：θsat由土壤有机质和矿物质含量以及各自的孔隙度决定，可表示为：

式中：fo为土壤有机质含量；θo为有机质孔隙度，取值0.9［63］；θm为矿物土孔隙度，由含砂量Psand决定，可表示为：

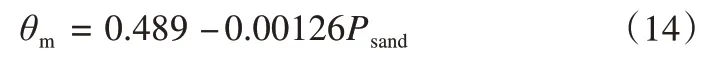
Ψsat为饱和土壤基质势，由土壤有机质和矿物质含量以及各自的基质势决定，可表示为：

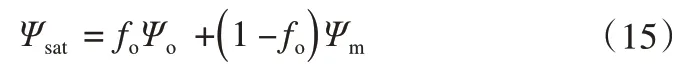
式中：Ψo为饱和有机质基质势，取值-10.3 mm［69］；Ψm为饱和矿物土基质势，由土壤中砂土含量Psand决定，可表示为：

B为Clapp-Hornberger 经验系数［63，70］，可 表示为：

式中：Bo取2.7［69］；Bm由土壤中黏土含量Pclay决定，可表示为：

2.4 模型参数率定

本研究中VIC-CAS 模型模拟的初始态文件根据站点的观测数据得到。模型的率定期选择1997年7月31日—1997年9月31日，验证期选择1997年10 月1 日—1998 年9 月29 日。率定后的主要参数如表1所示。

表1 VIC-CAS模型长江源区沱沱河站点率定后主要参数Table 1 Main parameters of VIC-CAS model after calibration at Tuotuohe station in the source area of Yangtze River

2.5 模型评估指标

利用率定后的模型进行土壤水热数值模拟，将1997年10月1日—1998 年9 月29 日作为模型的验证期分析模型的模拟效果和可靠性。根据丁永建等［71］对冻土区土壤水分含量变化的描述将模拟期土壤的温度和湿度变化分为四个阶段，分别是秋季降温阶段，1997 年9 月21 日到10 月21 日；冬季冻结阶段，1997年10月21日到1998年3月21日；春季升温阶段，1998 年3 月21 日到4 月21 日；夏季融化阶段，1997年4月21日到9月21日。

为了更直观地比较土壤温、湿度的模拟值和观测值，将土壤温度模拟值线性插值到观测值所在的深度。同时在分析土壤湿度时，将每层包含的各个深度土壤湿度观测的平均值与模拟值进行比较。

本文采用纳什效率系数（NSE）和均方根误差（RMSE）来作为评价指标。

其中，NSE 是评价水文模型模拟结果好坏的常用指标，计算公式如下：

NSE 的取值范围从负无穷到1。NSE 越接近1，模拟结果越好；接近0 表示模拟结果接近观测值的平均值水平，即总体结果可信，但模拟过程误差大；远小于0，则模型不可信。

RMSE 作为评估预测模型精度的指标，通常用来衡量真实值与模拟值之间的偏差，公式如下：

相关系数的取值范围从0 到正无穷。RMSE 越接近0，真实值与模拟值的偏差越小，模拟精度越高。

3 结果分析

3.1 导热率算法结果对比

图1为两种导热率算法下不同深度模拟的土壤逐时体积热通量对比。EBM 算法的热通量模拟值在7 个深度均低于原算法，热通量的减少表明EBM算法相较原算法阻碍了土壤冻融过程，表现为土壤温度在降温冻结阶段会偏高，在升温融化阶段会偏低。两者在20～60 cm 深度冻结期的热通量差值低于融化期，表明对冻结期土壤温度变化的影响小于融化期温度变化，而在60 cm 深度以下，冻结期和融化期的差值接近，对土壤温度变化影响差别较小。

图1 沱沱河站VIC-CAS算法和EBM算法模拟的7个深度土壤逐时热通量对比Fig.1 Comparisons in hourly soil heat fluxes between simulated by VIC-CAS algorithm and EBM algorithm at seven depths in Tuotuohe station

图2为两种导热率算法下不同深度模拟与观测的土壤日均温度对比。在80 cm 深度以上，VICCAS 算法温度模拟值在夏季融化期前40 天左右接近观测值，其余时段略低于观测值。在80 cm 及80 cm 深度以下，从秋季降温至冬季土壤温度下降至0 ℃，模拟值接近观测值；冬季土壤开始冻结至冻结期末，模拟值高于观测值；春季升温至夏季融化期末，模拟值低于观测值。7 个深度模拟结果总体较好，20～120 cm 深度模拟的土壤温度的NSE 大于0.9，130～160 cm 深度模拟的土壤温度的NSE 大于0.8。

图2 沱沱河站观测与VIC-CAS算法和EBM算法模拟的7个深度土壤日均温度对比Fig.2 Comparisons in daily soil average temperature between observed and simulated by VIC-CAS algorithm and EBM algorithm at seven depths in Tuotuohe station

EBM 算法模拟值在20 cm 和60 cm 深度整体接近观测值，在40 cm 深度，夏季融化期前三个月左右高于观测值，其余时段略低于观测值。在60 cm 深度以下，从秋季降温至春季升温，模拟值高于观测值；从春季升温至夏季融化期末，模拟值低于观测值。20～80 cm，NSE 大于0.9，模拟效果较好；在100～160 cm，NSE 低于0.8，且随深度增加，NSE 下降，模拟效果较差。

两种算法模拟的土壤温度趋势接近，从差值（EBM-VIC-CAS）上来看，在80 cm 深度以上，两种算法的差值在冬季冻结期和夏季融化期均为正值，原因是EBM算法对导热率的计算低于原算法，减缓了土壤的冻结过程，使冬季模拟的土壤温度偏高，这种影响持续到了夏季，尽管导热率的降低减缓了融化过程，但夏季模拟的温度仍高于原算法。冬季冻结期前两个月和夏季融化期前两个月差值较大，且冬季差值高于夏季，主要原因是土壤水分相变的初始阶段能量变化较大，对土壤的温度差异影响明显。同时在春末夏初土壤温度升至0值前后小段时间，差值表现为负值，在这段时间内土壤水分相变吸收大量热量，短时间内使土壤迅速降温。 在80 cm 深度及以下，随深度增加，冬季模拟的土壤温度对夏季土壤温度的影响在减小，夏季融化期两者差值表现为负值。同时由于深层土壤能量传递的滞后性，冬季和夏季差值的峰值时间在推迟，发生在冻结期和融化期的中段。

在80 cm 深度以上，EBM 算法的NSE 大于VICCAS 方案，同时RMSE 小于后者，EBM 算法的效果较优。在80 cm 深度，EBM 算法的模拟效果下降，NSE 小于VIC-CAS 算法，但仍大于0.9。在80 cm深度以下，两种算法的NSE 随深度增加而下降，EBM 算法在100 cm 深度最高为0.7858，小于0.8；而VIC-CAS 算法在3 个深度的NSE 均超过0.8。同时，3 个深度EBM 算法的RMSE 也大于后者，EBM算法在深层土壤模拟效果较差。

图3为两种导热率算法下三层土壤模拟与观测各层的日平均土壤湿度对比。表层（0～0.1 m）和中层土壤（0.1～0.6 m）两种算法的模拟值接近，而在下层土壤（0.6～1.6 m）在冬季冻结期有明显差异。导热率差异引起的土壤水分含量变化在表层不明显。两种算法在中层土壤的模拟值在冻结期整体接近观测值，模拟效果较好，而在其余时段低于观测值。两者的差值在冬季冻结期开始一个月内较明显，主要原因可能是导热率差异在冻结初期对土壤温度影响较明显，减缓了土壤水分的相变过程，使土壤中滞留的液态水含量较高。而在下层土壤，两种算法模拟结果皆高于观测值，VIC-CAS 算法模拟值在冻结期后半段至夏初土壤开始融化这段时间低于EBM 算法，更接近观测值。由于土壤能量传递的滞后性因素，下层土壤水分变化影响要延迟一段时间显现出来，土壤在冬季增加的水分是由于两种算法在冻结期土壤温度差值高于中层土壤，表明对土壤的冻结过程影响更大。在这种情况下，土壤水分的相变速率远小于中层土壤，滞留的液态水含量更高。

图3 沱沱河站观测与VIC-CAS算法和EBM算法模拟的三层土壤日均湿度对比Fig.3 Comparisons in daily soil average moisture between observed and simulated by VIC-CAS algorithm and EBM algorithm at three layers in Tuotuohe station

图4为三层土壤两种导热率算法下模拟的日均含冰量对比。两种算法在表层土壤的含冰量方面差别不大。EBM 算法在冬季前两个月的中层土壤含冰量明显低于原算法，原因是EBM 算法模拟的土壤温度在冻结初期略高于后者，表现出土壤水分相变过程减缓，使土壤含冰量计算偏低。EBM 算法在下层土壤的含冰量低于原算法，时间正是下层土壤水分含量变化的时段，冬季含冰量降低会减小冻结土壤的整体导热率，进一步减缓冻结过程。

图4 沱沱河站VIC-CAS算法和EBM算法模拟的三层土壤日均含冰量对比Fig.4 Comparisons in daily soil average ice content between observed and simulated by VIC-CAS algorithm and EBM algorithm at three layers in Tuotuohe station

图5为两种导热率算法下模拟与观测的逐时融化深度对比。观测的最大融化深度5 m 左右，VICCAS 算法的模拟最大融化深度8 m 左右，约高于观测值3 m；而EBM 算法模拟最大融化深度2.2 m 左右，约低于观测值2.8 m。EBM 算法模拟的融化深度变化趋势大于VIC-CAS 算法，且在数值上更接近观测值。VIC-CAS 算法对导热率的计算值较高，使融化期土壤的暖舌较深，EBM 算法在融化期对土壤的水热变化速率弱于VIC-CAS 算法，暖舌较浅，但更接近观测值。

图5 沱河站观测与VIC-CAS算法和EBM算法模拟的土壤逐时融化深度对比Fig.5 Comparisons in hourly soil melting depth between observed and simulated by VIC-CAS algorithm and EBM algorithm in Tuotuohe station

3.2 未冻水算法结果对比

图6为两种未冻水算法下模拟的不同深度土壤逐时土壤热通量对比。总体上7个深度两种算法的体积热通量差异并不明显，模拟趋势相近，结果表明未冻水含量差异对土壤能量传递数值的影响很小，对土壤温度的变化影响有限。

图6 沱沱河站VIC-CAS算法和CLM 5.0算法模拟的7个深度土壤逐时热通量对比Fig.6 Comparisons in hourly soil heat fluxes between simulated by VIC-CAS algorithm and CLM 5.0 algorithm at seven depths in Tuotuohe station

图7为两种未冻水算法下模拟与观测的不同深度土壤日均温度对比。7 个深度下两种算法模拟结果整体趋势接近，差异总体较小。两种算法的NSE和RMSE 差异较小，CLM 5.0 未冻水算法的NSE 和RMSE 在20 cm 和40 cm 深度稍优于VIC-CAS 算法，NSE 在0.9 以上。在60 cm 深度以下，稍差于原算法，但NSE仍大于0.8。

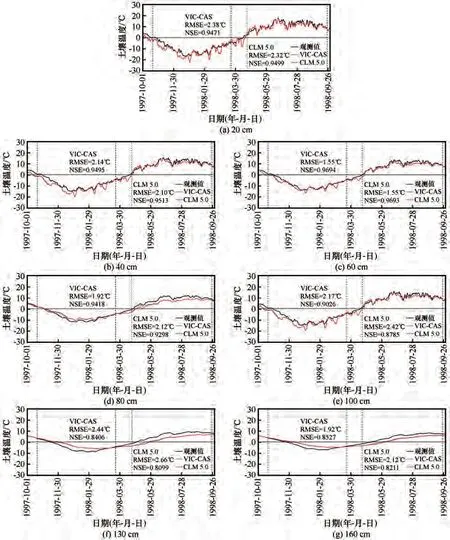
图7 沱沱河站观测与VIC-CAS算法和CLM 5.0算法模拟的7个深度土壤日均温度对比Fig.7 Comparisons in daily soil average wtemperature between observed and simulated by VIC-CAS algorithm and CLM 5.0 algorithm at seven depths in Tuotuohe station

图8为两种未冻水算法下三层土壤模拟与观测的各层平均土壤湿度对比。CLM 5.0 未冻水算法模拟的三层土壤的湿度均低于VIC-CAS 算法。CLM 5.0算法模拟的表层和中层土壤湿度的RMSE和NSE低于VIC-CAS算法，而下层土壤模拟效果优于后者。从差值（CLM 5.0-VIC-CAS）上来看，在表层和中层土壤，差异主要集中在冬季冻结期，原因是未冻水算法影响冬季土壤水分含量，且计算值较低。下层土壤差值低于前两层，主要原因是前两层土壤中的含冰量增加减少了下层土壤水分在冻结期的迁移，相比于原算法在下层土壤的模拟湿度偏高，在冬季更接近观测值。

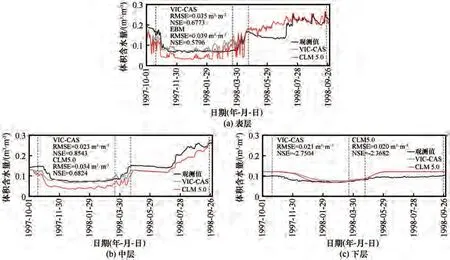
图8 沱沱河站观测与VIC-CAS算法和CLM 5.0算法模拟的三层土壤日均湿度对比Fig.8 Comparisons in daily soil average moisture between observed and simulated by VIC-CAS algorithm and CLM 5.0 algorithm at three layers in Tuotuohe station

图9为两种未冻水算法模拟的三层土壤日均含冰量对比。三层土壤模拟的含冰量变化趋势接近，且表现为随深度增加，土壤中冰的出现时间延迟。CLM 5.0 算法在表层和中层土壤模拟的含冰量在冻结期高于VIC-CAS 算法。而在下层土壤的含冰量相差不大。土壤中冰含量差异主要受冬季土壤中未冻水含量的影响，模拟的土壤中含冰量变化引起的相变能量传递差异也是间接因素。

图9 沱沱河站VIC-CAS算法和CLM 5.0算法模拟的三层土壤日均含冰量对比Fig.9 Comparisons in daily soil average ice content between observed and simulated by VIC-CAS algorithm and CLM 5.0 algorithm at three layers in Tuotuohe station

图10 为两种未冻水算法模拟与观测的逐时融化深度对比。两种算法融化深度模拟的趋势接近，CLM 5.0 算法融化深度略低于VIC-CAS 算法。两种算法融化深度在融化期中期高于观测值，在末期低于观测值，数值变化较大。上述结果表明，CLM 5.0 算法相较原算法对土壤中水热过程在土壤层中的能量传递速率和影响深度上变化不明显。

图10 沱沱河站观测与VIC-CAS算法和CLM 5.0算法模拟的土壤逐时融化深度对比Fig.10 Comparisons in hourly soil melting depth between observed and simulated by VIC-CAS algorithm and CLM 5.0 algorithm in Tuotuohe station

4 讨论

4.1 模型对土壤温度的模拟差异

多位研究者采用不同的陆面模型模拟了青藏高原多年冻土区的土壤温度，在唐古拉站高寒草甸区，刘洋等［72］基于SHAW 模型2007 年的结果显示，50～150 cm 深度土壤温度误差较大，而0～50 cm 和150 cm 深度以下模拟值和观测值拟合较好。胡国杰等［73］基于CoupModel模型在2008年的结果显示，0～105 cm 深度土壤模拟值和观测值吻合得较好，在105 cm 以下深度土壤的误差增大。马启民等［74］基于一维水热耦合模型2008 年的结果表明，0～50 cm深度土壤温度模拟效果较好，但90 cm 以下偏差增大。秦慧艳等［75］基于GIPL2 模型在可可西里站高寒草甸区2011—2012年的结果显示，0～100 cm模拟值与观测值相关性较高，120 cm 深度以下两者偏差增大，且模拟值稍高于观测值。郭林茂等［49］基于FEFLOW 模型在风火山高寒草甸区2006—2008 年的土壤温度模拟结果显示，0～20 cm 深度土壤的模拟精度低于20 cm深度以下土壤。

本文替换EBM 导热率算法后，在20～60 cm 深度，模拟值与观测值间的误差减小；在60～160 cm 深度，模拟值与观测值的误差增大。替换CLM 5.0 未冻水算法后与原算法的结果差异较小。与上述结果对比可以看出，GIPL2、SHAW 等模型与本文的模拟结果较为接近，即整体趋势模拟上相关性较一致，浅层土壤的精度高于深层土壤，且深层土壤的精度随深度增加而较差，其中，刘洋等［72］和马启民等［74］的结果在深度上更接近本文。FEFLOW 模型的结果与本文结果相反，在深层土壤温度模拟精度优于浅层。

造成这种结果可能的原因是：（1）各层输入的土壤水热参数存在误差。多年冻土区土壤存在异质性，不同深度土壤特性差异较大。本文模拟时将土壤柱划分为10 cm、50 cm、100 cm 三层土壤；秦艳慧等［75］根据文献［76］按5 cm、20 cm、大于100 cm 划分土壤层；胡国杰等［73］、马启民等［74］按不同深度划分土壤厚度，在浅层土壤划分厚度较浅，而深层土壤划分较厚，输入的土壤参数不能代表各层的真实情况，这导致了浅层土壤的模拟精度高于深层土壤。（2）模型中冻土算法热量平衡方程大都来自于Stefan 的热传导方程，在计算中各层土壤参数除因深度划分不均匀引起的误差外，自身与实际值也存在偏差，热传导方程再计算土壤中热量由上而下或由下而上传递过程时，这种误差会不断累积。（3）研究区植被为高寒草甸，根系在0～30 cm 左右，影响浅层土壤的热性质。相比较其他模型，郭林茂等［49］认为FEFLOW 模型缺少植被输入是影响浅层土壤的模拟结果的重要原因。

4.2 模型对土壤湿度的模拟差异

对青藏高原多年冻土湿度的模拟结果中，刘洋等［72］的结果表明SHAW 模型在5～20 cm 土壤的模拟值低于观测值，而70～210 cm 土壤冻融期模拟值高于观测值。胡国杰等［73］的结果表明CoupModel模型在5～20 cm 的模拟值低于观测值，而在70 cm以下接近观测值。马启民等［74］的结果显示0～50 cm的模拟值在冻结期接近观测值，而50 cm 以下的模拟值在冻结期高于观测值。

本文替换未冻水算法对土壤湿度的差异主要表现在土壤冻结期到融化期前，融化期湿度变化较小，与刘火霖等［54］未冻水参数化方案替换的结果基本一致。对比他人的模拟结果可以看出，替换EBM导热率算法后，0～60 cm 土壤湿度在冻结期结果上优于上述三种模型；60～160 cm 冻结期的模拟值高于观测值，与刘洋等［72］、马启民等［74］的结果接近。替换CLM 5.0 未冻水算法后，0～60 cm 土壤模拟值低于观测值，与刘洋等［72］、胡国杰等［73］、马启民等［74］的结果相同；60～160 cm 土壤模拟值接近观测值，与胡国杰等［73］的结果接近。

出现上述差异的原因可能是：（1）VIC-CAS 模型输出的是三层土壤的平均湿度，反映的是三层土壤中各层整体的水分变化情况，不能表现出土壤水分随深度的变化及各深度间水分的差异性。而刘洋等［72］、胡国杰等［73］、马启民等［74］利用的模型能够模拟各深度的土壤水分，与观测值的比较在结果上可能更好。（2）在替换两种算法前，VIC-CAS 模型默认的土壤湿度模拟值在冻结期接近观测值，表现了VIC-CAS 模型在冻结期能够较好模拟土壤水分的优点。替换EBM 导热率算法主要对60～160 cm 土壤有影响，使水分模拟偏高，表现出SHAW 等模型在深层土壤模拟较差的缺点，原因可能是替换的导热率方案计算值相比原方案与实际值偏差增大，并在深层表现得更为明显。替换CLM 5.0 未冻水算法，降低了0～60 cm 土壤湿度的模拟精度，但提高了60～160 cm 的模拟精度，与胡国杰等［73］的结果接近。可能原因是CLM 5.0 未冻水算法水分模拟自身的缺点，熊健胜等［77］认为CLM 模型模拟多年冻土时，冻结期含水量被低估，而含冰量被高估，但偏低的模拟值弥补了VIC-CAS 模型在深层土壤模拟值较高的缺点，使下层土壤的模拟结果反而变好。胡国杰等［73］利用的CoupModel 模型的土壤水分模拟值整体偏低，且深层的土壤模拟精度高于浅层土壤，因此与本文的结果接近。

4.3 模型中冰含量对土壤热特性的影响

冰作为不透水面，显著减低土壤水分的迁移，同时冰的导热率是水的4 倍，影响冻结土壤的总体导热性。本文在替换未冻水算法后，模拟结果图9中0～60 cm 土壤含冰量有所增加，但图6 和图7 中，20～160 cm 各深度替换未冻水方案前后模拟的热通量和温度的差异较小。

李振坤［78］在改则地区的研究表明CLM 3.0 参数化方案改进前后0～80 cm 土壤温度模拟值间的相关系数大于0.9，含冰量变化对浅层土壤温度变化较小。本文的结果对比上述结果的差异更小，两种未冻水方案下观测值与模拟值间相关系数差值最大在0.03 左右，由CLM 未冻水方案的缺点来看，实际的含冰量比模拟值更低，含冰量对土壤导热性能的影响可能更小。

5 结论

本研究分别用EBM 导热率算法和CLM 5.0 的未冻水算法替换以VIC-CAS 模型为基础的导热率和未冻水算法，对长江源区沱沱河站进行了为期一年的单点数值模拟试验，主要结论如下：

（1）EBM 算法导热率低于原算法，会减缓土壤的冻融过程，对不同深度土壤温度影响较明显，在土壤湿度模拟上，对深层土壤计算数值较高，而浅层变化不大。算法提升了浅层土壤温度的模拟效果，但使深层土壤温度和湿度模拟效果变差。

（2）CLM 5.0 算法未冻水数值低于原算法，主要减少了冻结期土壤的水分，但土壤水分的变化对土壤能量传递影响有限，与原算法土壤温度较接近。算法对深层土壤湿度的模拟效果变好，但浅层土壤湿度模拟效果变差。

（3）本文虽然替换了两种土壤参数算法，但在土壤湿度的模拟效果上并没有显著的改进。通过对比可以看出两种算法与原算法各有优缺点，EBM导热率算法需要改进误差产生的累积效应对深层土壤的影响，而CLM 5.0 未冻水算法在对浅层土壤的湿度模拟上过低仍是个需要进一步考虑的问题。