MATLAB在圆锥曲线教学中的应用

吕士宝

MATLAB是一个强大的数学软件，常用于分析数 据、绘制图形、处理图形、进行矩阵运算等.高中圆锥曲线知识较为抽象，学生学习起来比较困难，教师可利用MATLAB来辅助教学，借助MATLAB强大的作图功能，来激发学生的学习兴趣，突破教学的重难点.

一、利用MATLAB激發学生的学习兴趣

很多圆锥曲线知识较为抽象，仅靠口头讲解和黑板板书，学生很难掌握所学的知识，教师可将MATLAB应用于课堂教学中，利用 MATLAB 绘制出不同的图形，以直观或动态的形式演示出来，这样能有效地吸引学生的注意力，激发其学习的兴趣.学生通过观察，便会对圆锥曲线的几何形式、几何性质具有初步的印象，为对椭圆的方程、图形、性质等的研究作好铺垫.

例如，在教学“椭圆的几何性质”时，笔者利用MATLAB辅助教学.首先设计好MATLAB程序代码，其运行程序如下：

t=linspace（0，2*pi，1000）;

x=4*cos（t）;

y=sin（t）;

plot（x，y），grid on

hold on;

t=linspace（0，2*pi，1000）;

x=4*cos（t）;

y=2*sin（t）;

plot（x，y），grid on

hold on;

t=linspace（0，2*pi，1000）;

x=4*cos（t）;

y=3*sin（t）;

plot（x，y），grid on

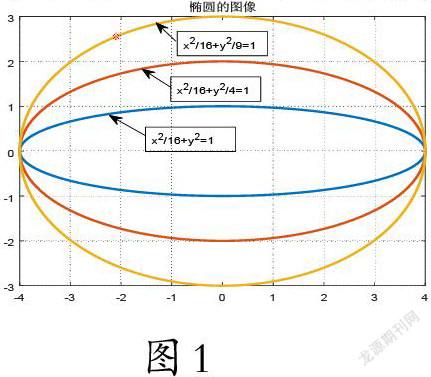
借助 MATLAB 作出如图 1 所示的 3 个椭圆，并让学生通过观察图形，对椭圆的图形进行讨论.动态的图形演示，能有效地激发学生的学习兴趣，使他们快速进入良好的学习状态，通过观察、讨论，得出结论：（1）椭圆是轴对称图形，其对称轴为 x 轴与 y 轴;也是中心对称图形，坐标原点是其对称中心;（2）若 a、b 分别是椭圆的长半轴长和短半轴长，则椭圆位于直线 x = ±a 和 y = ±b 所围成的矩形区域内;（3）当 e 越接近于1时，椭圆越扁，e 越接近0，椭圆越圆.

利用MATLAB绘制出大量的椭圆图形，引导学生对其进行对比、分析，不仅能激发其学习兴趣，还能让他们了解椭圆的图形，培养直观想象能力.

二、借助MATLAB突破教学的重难点

在讲解重难点知识时，教师可借助MATLAB来辅助教学，改变MATLAB 程序中的数据，如圆锥曲线方程中 a、b、e 的值、将不同情况下的曲线展示出来，引导学生对其进行观察、分析，总结规律，挖掘出知识的本质，从而突破教学的重难点.

例如，在教学“双曲线的几何性质”时，笔者设计了如下的 MATLAB程序：

a=4;

b=3;

c=sqrt（a^2+b^2）;

syms x y

subplot（1，3，1）;h=ezplot（x^2/a^2- y^2/b^2==1，[- 10，10]）

hold on;axis equal;

plot（[-10：0.1：10]，b/a.*[-10：0.1：10]）

plot（[-10：0.1：10]，-b/a.*[-10：0.1：10]）

将MATLAB应用于圆锥曲线教学中，不仅可以丰富教学的内容，降低学生学习的难度，还有助于培养学生的数形结合能力，从而达到提高教学质量的目的.

（作者单位：甘肃省临夏市城郊镇临夏回民中学）