考虑右转汇入车辆的干线协调控制与速度引导集成研究

杨晓芳，李婷瑞

（上海理工大学管理学院，上海 200093）

0 引言

干线协调控制是常用的缓解城市交通拥堵、提高城市道路通行能力的交通控制方法。然而大多数干线信号协调无法克服车辆到达的随机性和车辆速度波动性带来的不利影响。随着车路协同系统（Cooperative Vehicle Infrastructure System,CVIS）的发展，结合车路协同与传统的信号协调实现时空资源的合理分配可减少上述不利影响，因此对干线协调控制与速度引导的集成优化研究很有必要。

目前，交叉口信号控制与速度引导的集成研究可分为被动控制与主动控制两大类，进一步可分为单交口控制和多交叉口控制。被动控制的交叉口信号控制方案不变，以减少停车次数[1]、等待时间[2]、油耗最少[3-4]等为目标，以单车[1-2]、车队[5-6]为对象对车辆进行速度引导，上述研究对提升交叉口的运行效率有一定效果，但未考虑车辆排队的影响。He 等人[7]进行了考虑车辆排队的干线协调控制与速度引导集成研究，但没有考虑转向汇入车辆对干线车流连续通行的影响。主动控制是在被动控制的基础上对车流数据进行分析，实时调整信号方案，实现交叉口信号和车辆速度引导的协同控制[8-13]，涉及滚动时域法[8]、模糊控制法[11]等方法。在集成研究中，吴伟等人[13]提出了干线交通流饱和及非饱和情况下的速度引导模型，但是没有考虑相交道路转向汇入车辆对车流饱和及非饱和的影响。以往研究提升非协调相位运行效益和降低对干线车流的影响时，一般采用优化相序相位的方法[14]，没有使用速度引导策略。Li 等人[15]构建了车联网环境下的交通信号协调系统，却没有与速度引导集成，没有充分发挥速度引导的优势。

综上，已有的交叉口信号控制与速度引导集成研究中，未考虑相交道路转向汇入车流的影响；已有的相交道路转向汇入车流对干线协调控制影响的研究中，未考虑与速度引导集成优化。为此，本文针对相交道路右转汇入车辆较多进而影响干线协调控制这一现实情况，提出干线协调控制与速度引导的集成优化模型，探究相交道路右转汇入车辆较多时干线绿灯时间的分配问题，并分别提出干线车辆及右转汇入车辆的速度引导模型，以减少右转车辆对干线协调控制的影响，提升可通行时间内交叉口的通行效率，使干线交叉口时空资源得到更合理的分配。

1 问题描述

相交道路右转汇入车流由于不受信号灯控制，容易影响干线直行车流的通行效率。图1 所示为右转汇入车辆与干线直行车辆行驶轨迹，za,zb,zc,zd代表由南至北直行的车辆，ya,yb代表由交叉口右转汇入干线直行的车辆，车辆za,zb,zc,zd在绿波时段内在干线直行，本应不停车通过下游交叉口，但由于相交道路右转汇入车辆ya,yb不受信号灯控制，在交叉口i汇入直行车流，插到za与zb之间在绿波时段内通过交叉口，导致本可连续通过交叉口的直行车辆在下游交叉口处排队。此时如果相交道路右转汇入车辆较多，导致交叉口下一周期干线直行车辆无法连续通过交叉口i+1，会造成交叉口的排队，进而降低干线绿波协调效益。

图1 右转汇入车辆与干线直行车辆行驶轨迹

为解决上述问题，本文将基于干线绿波协调控制模型，分别给出干线直行车辆和相交道路右转汇入车辆的速度引导模型，以绿波带宽最大为目标实现干线车辆和右转汇入车辆的协同优化，提高干线的运行效率。为简化问题，采用如下假设：

（1）车辆均严格服从车速引导策略；

（2）不考虑从道路旁建筑内驶入路段内的车辆；

（3）假设车辆在进入引导区域后不再换道。

2 右转汇入车辆可通行时间及车速引导策略

2.1 右转汇入车辆可通行时间

图2为右转汇入车辆可通行时间示意图。图2中，L1为交叉口间的距离，wi,wi+1为交叉口i,i+1上行方向绿灯开始时刻到绿波带左侧边缘的时间间隔，为交叉口i+1 当前周期直行方向绿灯开始时间和红灯开始时间，为交叉口i+1 下一周期直行方向绿灯开始时间和红灯开始时间。对右转汇入车辆进行引导，一方面是为了减少对干线直行车辆的干扰，需要避免右转汇入车辆在干线绿波时段内驶入交叉口i；另一方面是避免对右转汇入车辆自身造成较大延误，因此可引导右转汇入车辆在非绿波时段内通过交叉口i和i+1。右转汇入车辆的可通行时间T为在干线直行车流之后、在交叉口i+1绿灯结束之前通过交叉口的时间。

图2 右转汇入车辆可通行时间示意图

2.2 车速引导策略

车速引导流程如图3所示，主要涉及4个阶段：

图3 车速引导流程图

（1）初始通行时间的确定：根据车流量分配信号灯，并确定初始干线直行车辆及相交道路右转汇入车辆在交叉口的可通行时间；

（2）车速优化：根据交叉口信号灯状态及车辆位置、速度等信息判断当前车辆是否能通过交叉口，利用车速引导模型优化相关车辆速度；

（3）车辆引导：利用优化后的速度对相关车辆实施引导，至其通过交叉口。

（4）判断通行时间是否需要调整：如果相交道路右转车辆进入交叉口时发生排队现象，则调整可通行时间，重复步骤（2）～（4）。

3 优化模型

3.1 绿波带宽模型

速度引导模型以绿波带宽模型为基础，绿波协调控制时空图如图4所示。

图4 绿波协调控制时空图

本文以红灯中点为标准定义相位差，建立以下等式约束[12]：

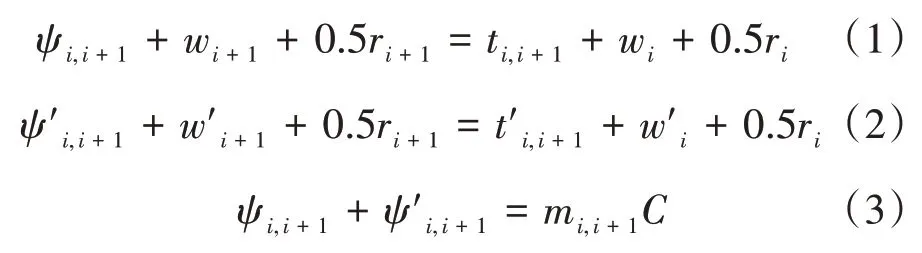
式（1）～式（3）中：C为公共周期时长（s）；mi,i+1为交叉口i和交叉口i+1 的相位差方程式系数，取正整数；其他参数含义同前。

wi,w′i,wi+1,w′i+1既要满足交叉口排队车辆的清空时间，又要满足有效绿灯时间约束：

式（4）～式（7）中，τi,τi+1分别为上行方向交叉口i、交叉口i+1 的排队清空时间；τ′i,τ′i+1分别为下行方向交叉口i、交叉口i+1 协调相位排队清空时间；gi,gi+1分别为交叉口i、交叉口i+1 协调相位的有效绿灯时间；其他参数含义同前。

目标函数为绿波带宽最大：

约束条件为式（1）～式（7）。

3.2 速度引导模型

3.2.1 直行车辆速度引导模型

对于干线直行车辆，引导车辆加速或减速行驶，使得车辆在绿波时间段内到达第一个交叉口，然后以绿波速度不停车通过下一交叉口，以减少车辆的停车次数和停车时长。直行车辆速度引导示意图如图5 所示，图中ta为每个周期内直行车辆需减速行驶的结束时刻，也是车辆按自由流速度行驶的开始时刻；tb为车辆按自由流速度行驶的结束时刻，也是车辆需加速行驶的开始时刻；tc为车辆加速行驶的结束时刻，也是车辆需减速行驶的开始时刻。

图5 直行车辆速度引导示意图

直行车辆的引导策略如下：

（1）车辆在tc～ta时刻进入引导区域时，以最大速度无法在当前绿灯期间通过交叉口i，此时引导车辆减速行驶至绿波开始时刻，继而以绿波速度通过下一个交叉口。引导速度计算公式为：

式（9）～式（11）中：v(i,j)为交叉口i协调车辆j的引导速度（km/h）；L0为直行车辆引导距离（m）；t为车辆进入引导区域时刻；为图5 所示的交叉口i直行方向绿灯开始时间；为交叉口i下一周期直行绿灯开始时间；v0为自由流速度（km/h）；vmax为路段允许的最大速度（km/h）；其他参数含义同前。

（2）车辆在ta～tb时刻进入引导区域时，按照自由流速度可以通过交叉口，无需进行速度引导，此时：

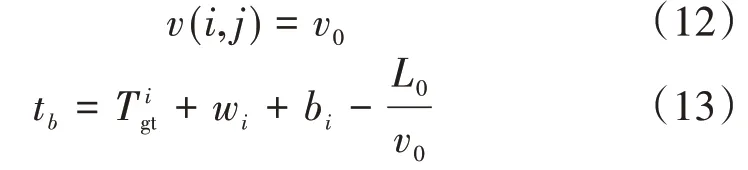
（3）车辆在tb～tc时刻进入引导区域时，可加速在当前绿波时段内通过交叉口，因此对车辆进行加速引导，此时引导速度计算公式为：

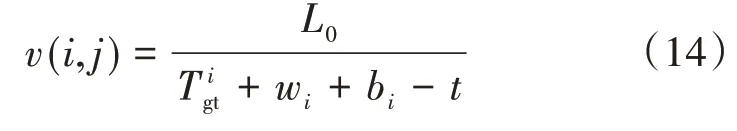
3.2.2 右转汇入车辆速度引导模型

按照第2 节中的引导策略，将绿波之后的绿灯时间分配给相交道路右转汇入车辆。此时会产生两种情况，第一种情况如图6（a）所示，当用于右转的直行时间T满足右转车辆的通行，在不影响或提高右转通行效率的条件下提高干线直行车辆的通行效率，此时T通过式（15）（a）计算；第二种情况如图6（b）所示，当右转车辆较多且绿波之后的绿灯时间较少时，右转汇入车辆可通行时间无法满足通行需求，此时可缩短一定的绿波时间ΔT，进而确定用于上游交叉口i右转汇入车辆的直行总绿灯时间T，如式（15）（b）所示，通过交叉口i的信号配时进行右转汇入车辆的速度引导。应注意的是，缩短绿波时间ΔT后不能降低干线直行车辆的通行效率，且右转汇入车流延误的增加要少于50%。

式（15）～式（16）中：T为右转汇入车辆的直行总绿灯时间（s）；为图6 所示的交叉口i+1直行方向绿灯结束时间；k为决定绿波带宽的影响因子，本文取整数；ΔT（s）为缩短的绿波时间，即绿波带中用于相交道路右转汇入车辆的时间，与右转汇入车流量成正比，与直行车流量成反比；qr,qz分别为相交道路右转及直行交通量（pcu/h）；n为直行车道数；其他参数含义同前。

图6 右转汇入车辆车速引导示意图

图6 中，d0为右转汇入车流引导距离；t1为右转汇入车辆需减速行驶的结束时刻，也是车辆按自由流速度行驶的开始时刻；t2为车辆按每个周期内自由流速度行驶的结束时刻，也是车辆需加速行驶的开始时刻；t3为车辆加速行驶的结束时刻，也是车辆需减速行驶的开始时刻；ts为绿波结束时刻；te为右转可通行时间结束时刻。右转汇入车辆的引导策略如下：

（1）车辆在t3～t1时刻进入引导区域时需减速，使得行驶至交叉口i的时间刚好为右转车辆通行的开始时间（即T的左侧ts）。此时引导速度计算公式为：

（2）车辆在t1～t2时刻进入引导区域时，以自由流速度通过交叉口，无需引导，此时：

（3）车辆在t2～t3时刻进入引导区域时，需加速在右转车辆通行结束前（即T的右侧te）通过。此时引导速度计算公式为：

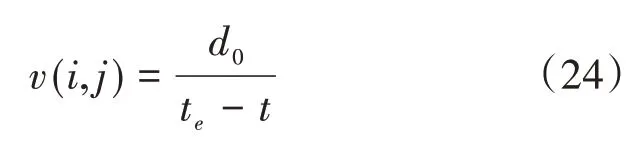
车辆通过交叉口i后，为避免在交叉口i+1处停车等待，以绿波速度行驶至交叉口i+1。实行引导后的车速v(i,j)应满足最大车速vmax和最小车速vmin的约束。

4 实例分析

4.1 案例概况

现选取有右转专用车道的连续交叉口进行模型验证。本文所选的山东威海市海滨路-城阳路交叉口、海滨路-胶州路交叉口位于威海市经济技术开发区东侧海岸线，均为T 形交叉口（见图7），交叉口渠化如图8所示。

图7 实验交叉口地理位置

图8 交叉口渠化图

各交叉口在早高峰7:20—8:20 的流量如表1所示。根据交叉口渠化图和交叉口流量表采用Webster 法求得各交叉口信号配时方案，如表2所示。

表1 各交叉口流量调查结果 单位：pcu·h-1

表2 各交叉口信号配时方案

4.2 结果分析

为检验本文提出的考虑右转汇入车辆的干线信号协调控制与速度引导集成模型的有效性，本文以Vissim4.3 为仿真平台，使用Matlab 及Vissim-Com 接口进行二次开发，将本文模型的评价结果与Maxband 模型进行比较。仿真设定干道方向车速引导区域为交叉口停车线上游300m 处，相交道路右转车速引导区域为停车线上游250m处；车辆初始速度为40km/h，最小与最大引导速度分别为20km/h,60km/h；直行车道饱和流率为1 650pcu/h，右转车道饱和流率为1 250pcu/h，仿真周期为1 800s。对主干道直行车辆、交叉口①相交道路右转车辆、交叉口②相交道路右转车辆三者的平均延误、平均排队长度、平均停车次数进行比较，结果如表3所示。

表3 不同模型的仿真结果对比

由表3 可知，随着影响右转汇入车辆可通行时间的因子k值的增大，干线直行车流的平均延误增大，相交道路右转车流的平均延误降低。本次实验取对相交道路右转延误影响最小的k值作为最优值，当前流量条件下，k=10 时模型的效果最优。在对相交道路右转汇入车辆影响最小的前提下，干道直行车辆的平均延误降低17.4%，平均排队长度减少36.8%；相交道路右转车辆的平均延误增加12%，平均停车次数减少60.5%，这是因为限制了相交道路右转车辆的通行时间，同时通过速度引导，减少了右转车辆的停车次数。

4.3 灵敏度分析

由4.2 节可知，本文提出的模型可提升交叉口的通行效率，本节进一步研究该模型的适用性。使用交通量和k的取值作为评估因素，设置直行交通量从1 700pcu/h增加至2 500pcu/h，相交道路右转交通量从285pcu/h 增加至450pcu/h，k的取值从5 增加至18，将各流量条件下Maxband模型与本文模型的最优解进行对比，分析车辆平均延误及平均排队长度的变化。实验结果如图9所示。

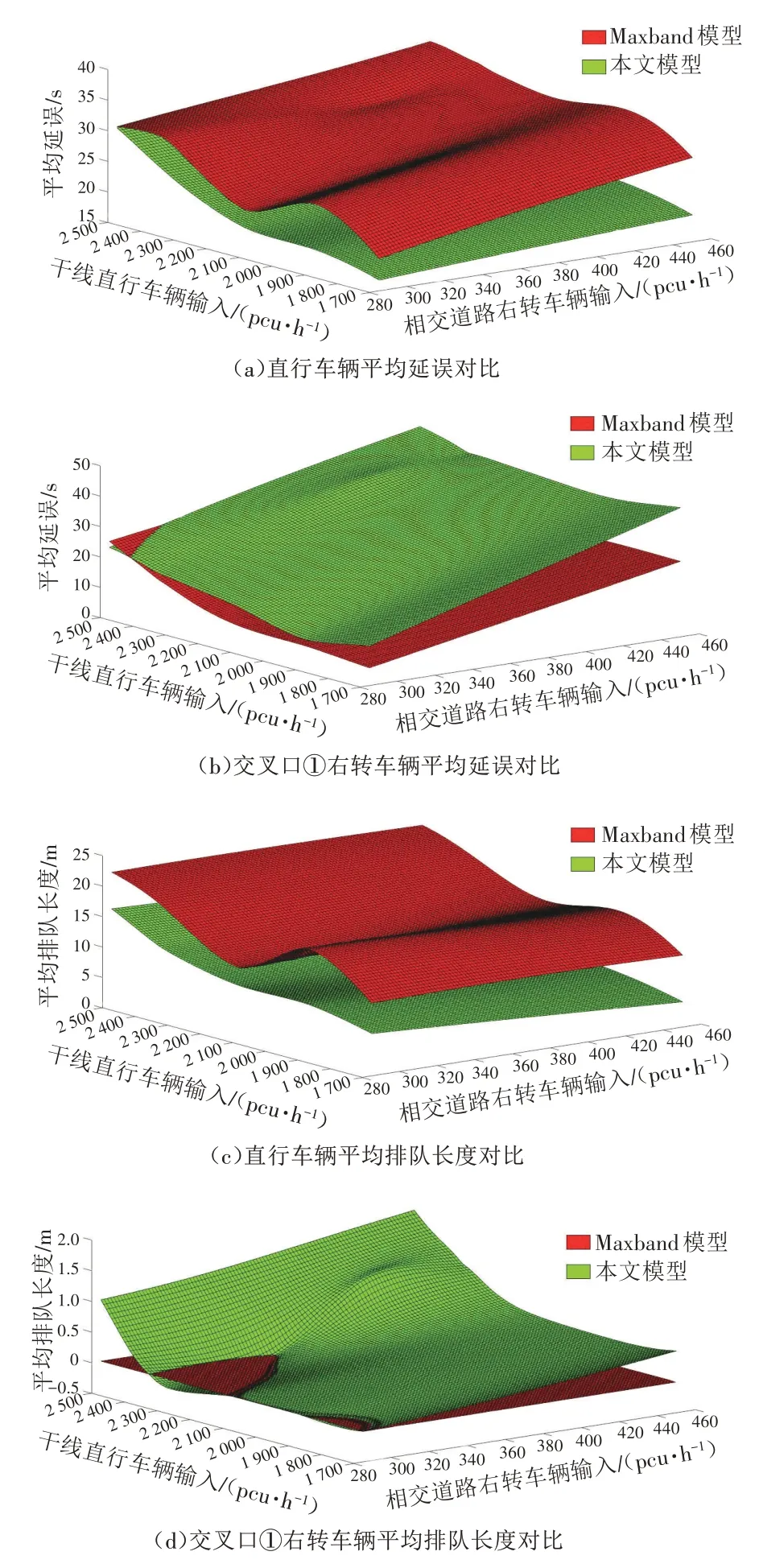
图9 仿真结果对比图

如图9（a）所示，在干道直行交通量不变的情况下增加相交道路右转交通量，Maxband 模型中直行车辆的平均延误增加，说明研究本文提出的问题是有必要的；由图9（a）和（c）可知，通过车速引导与干线信号协调控制的集成优化，交叉口干线直行车辆的平均延误和排队长度均有不同程度的降低，表明本文模型对减少相交道路右转车辆对干线直行车辆的影响是有效的。由图9（b）和（d）可知，本文模型对相交道路右转车辆的通行效率有一定的影响，一方面是为了提升干线直行车辆的通行效率，限制了相交道路右转车辆的通行时间；另一方面是实验路段有较多换道车辆，右转车辆汇入到干线直行路段后的行驶受到换道车辆的影响，部分车辆无法在下游交叉口绿灯结束前通过交叉口。当右转汇入车辆与直行车辆交通量均较大时，如直行车流量为本次实验条件下的2 354pcu/h，继续增加交叉口①西进口右转汇入车流量，当右转车流量大于550pcu/h时，右转车流延误增加超过50%，模型不再适用。k的最佳取值根据车流量的不同而变化，且具有随着车流量的增加，k的取值也变大的规律。这是因为k的取值与用于直行车辆绿灯时间的长短有关，k的取值越大，用于直行车辆的绿灯时间也越长。通过不同流量条件下k的最佳取值，可得实验路口k的取值与相交道路右转车流量qr、直行车流量qz、直行车道数n的关系为：

式（26）适用于本次案例，未来可按照本文方法进行实验得到k的最优取值。

5 结语

本文针对相交道路右转车辆汇入干道行驶进而影响绿波控制效率这一情况，提出了右转车辆速度引导模型。为保证主干道直行车流的绿波行驶时间，结合速度引导模型控制每一周期相交道路右转车辆汇入干道的时间，通过Vissim 与Matlab仿真验证，结果表明右转汇入与直行车辆的通行效率均获得了提升。经仿真实验发现，模型的效果与k的取值有关，且k的取值具有随着右转车辆输入的增加而变大的规律，本文模型适用于右转汇入车流量小于550pcu/h的情况。

本文仅对T 形交叉口进行了研究，而在十字交叉口中还存在直行及右转的混合车道，今后需对此深入探讨。另外，本文假设车辆均严格服从车速引导策略，但车路协同环境目前仍未普及，未来也将经历网联车辆与非网联车辆混行阶段，故需进一步研究混行阶段车辆控制问题。