非线性薛定谔方程的光纤解和调制不稳定性
秦春艳
宿州学院数学与统计学院,安徽宿州,234000
近年来,在非线性光学中,光纤孤子一直是广泛研究的课题,光纤孤子包括亮孤子型和暗孤子型脉冲,可以分别在一般色散介质和非一般色散介质中传播。它们在光纤通信领域引起了强烈的反响,如今各种通信方式,如电信和互联网传输工具已经变得越来越发达,这可能要归功于光孤子领域的研究[1-2]。非线性薛定谔方程在这些研究中具有重要的理论意义,它可以描述光脉冲的一些动态行为。这类方程包括一些重要的性质,如皮秒脉冲、群速度色散和自相位调制等。此外,在薛定谔方程族中,存在许多不同的类型,主要包括Kerr非线性、三次方程非线性和对数非线性等。这些非线性薛定谔方程可以表示一些光学传播中非常有趣的现象,例如水波、玻色-爱因斯坦凝聚和等离子体物理学[3-4]。几种经典类型的薛定谔方程引起了数学家和物理学家们的关注,这些方程主要包括与三次-五次非线性相关的广义薛定谔方程、与任意非线性相关的强制薛定谔方程和与非Kerr项相关的高阶薛定谔方程[5-7]。事实上,它不同于普通的非线性薛定谔方程,那些存在非Kerr效应的方程被验证为不完全可积系统,不能使用反散射变换构造精确解。
本文研究如下形式的非线性薛定谔方程[8]
i(ψt+Cgψx)+μψxx+ν|ψ|2ψ=0
(1)
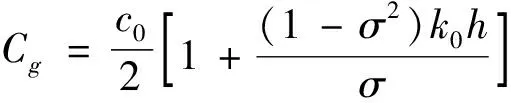
1 稳定性分析解
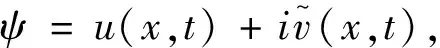
(2)
(3)
这里dω=dtdx,λ是实常数。把(2)式与(3)式结合起来,可得
由此得到一个拉格朗日算符L:
为了验证后面的计算,将拉格朗日算符L应用到如下系统:
接下来为构造方程(1)的光纤解,引入文献[5,15]中的假设:
ψ=Ω(x,t)eiφ(x,t),φ(x,t)=k1x-ωt+θ
(4)
这里Ω=Ω(x,t)表示脉冲的形状,φ(x,t)表示孤子的相位部分。其中k1,ω和θ分别是波数、频率和相位中心。因此,从方程(4)可求出它的偏导数,把这些偏导数代入到方程(1)中,最后从所得到的方程中分别收集实部和虚部,即
2μk1Ωx+Ωt+CgΩx=0,vΩ3-μk12Ω-k1CgΩ+ωΩ+μΩxx=0
(5)
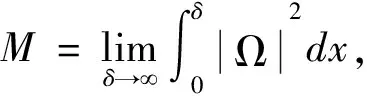
1.1 亮孤子解
亮光纤孤子被熟知为bell-型孤子,而且由于对长的空间距离没有相变化,所以也被熟知为非拓扑孤子。
定理1非线性薛定谔方程(1)的亮孤子解为
ei[k1x+(B12μ-k12μ-Cgk1)t+θ]
证明:对亮孤子解,基于文献[15]的假设,取
Ω(x,t)=Asechpτ
(6)
其中τ=B1(x-rt),A为波幅,B1为孤子的逆宽度,r是波速。通过(6)式,可以得到关于Ω的一些导数,这样系统(5)就可以写成:
2ApB1k1μsechp(B1(x-rt))tanh(B1(x-rt))-ApB1rsechp(B1(x-rt))·tanh(B1(x-rt))+CgApB1sechp(B1(x-rt))tanh(B1(x-rt))=0
(7)
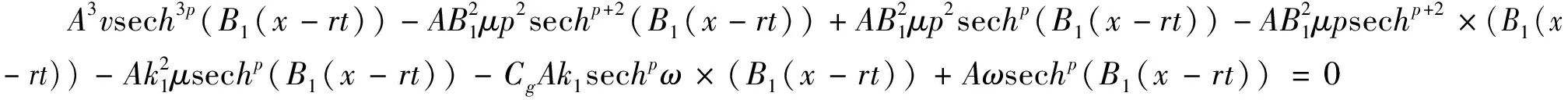
(8)
对于方程(7),将sechp(B1(x-rt))tanh(B1(x-rt))的系数设为零。在(8)式中,令指数3p等于p+2,然后得到p=1.通过把相同的项组合起来,容易得到:
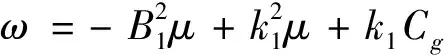
(9)
最后,得出方程(1)的一个亮孤子解由下式给出:
ei[k1x+(B12μ-k12μ-Cgk1)t+θ]
其中振幅A、宽度B1、速度r和频率ω分别由(9)式确定相应的约束条件,而这些约束参数确保孤子的存在。为更好地分析光纤孤子的性质,通过选取合适的参数,亮孤子解的图片绘制如图1。

图1 亮孤子解的图像
1.2 暗孤子解
暗孤子解,在非线性光学内容中,它被熟知为非拓扑孤子。类似地,为获得方程(1)暗孤波解,基于文献[15]中的假设,取Ω(x,t)=Atanhpτ,其中τ与亮孤子解的部分相同。根据同样的计算得到:
因此,非线性薛定谔方程(1)的暗孤子解形式如下:
为更好地分析光纤孤子的性质,非线性薛定谔方程(1)在参数条件g=1,k0=ln(1/2),k1=1,h=1,c=1,B1=1,θ=0下,暗孤子解的图片绘制如图2。

图2 暗孤子解的图像
2 复 解
定理2非线性薛定谔方程的复解为:
证明:在这一部分,考虑了非线性薛定谔方程的复解问题。基于文献[9]中的性质,ψ(x,t)表示为
ψ(x,t)=f(ξ)exp(iφ)
ξ=α1x-βt+θ0,φ=l1x-vt+θ1
把上述表达式代入到方程(1),然后可以得到:
(10)
平衡非线性项f3和最高阶导数f″的线性项,并假设常微分方程(10)解的形式是:
f=a0+a1Y,Y=tanhξ.把f代入到方程(10),通过计算可以得到下面的一些限制条件
则非线性薛定谔方程(1)的复解:
3 调制不稳定性
一些研究表明许多非线性薛定谔方程都存在一个不稳定性因子,这就导致了在稳定状态下的一个调制,从而在非线性项和色散效应之间产生一个相互作用。所以,有必要构造与非线性系统(1)相关的调制不稳定性。利用文献[16]中的结果,引入一个稳态函数:
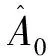
(11)
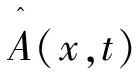
(12)
其中a1,a2分别表示扰动的波数和波频率。从线性演化方程(11)很容易得出一个色散关系a1=a1(a2),它决定了关于波数a1的时间振荡eia1x如何与空间振荡eia2t相关。把式(12)代入方程(11),得到色散关系如下:
(13)
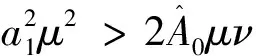
4 结 论
研究了非线性薛定谔方程,该方程可用于表征与弱非线性恢复力相关的长波水波。基于拟设方法,推导出它的亮解和暗解。同时,通过考虑双曲正切函数,提供了一种方法来找到它的复解。此外,构造了方程(1)的拉格朗日形式和不变变分原理。最后,对于所得到的结果使用调制不稳定方法。通过应用稳定性分析,得到了相应的稳定和不稳定的条件,希望此结论对光纤通信的发展有所帮助。

