基于子集模拟的建设工程项目多资源均衡优化算法

王家 刘可心 张学清 陈涛

摘要：为高效、稳定地求解建设工程项目管理过程中的多资源均衡问题，提出一种基于子集模拟的优化算法.多资源均衡问题中，如直接采用工序计划开始时间作为决策变量，在优化算法的实现时易违反工序间的逻辑关系.为避免该问题，本文采用工序计划开始时间的间隔率变量表示（在二者的映射中考虑工序间的逻辑关系），并据此建立间隔率变量表示的建设工程项目多资源均衡优化模型，以简化基于子集模拟的优化算法的操作流程.通过算例验证，与目前应用较广的遗传算法相比，本文提出的优化算法在最优解的获取稳定性上有較大改进.

关键词：资源均衡问题；子集模拟；马尔科夫链蒙特卡罗；间隔率；遗传算法

中图分类号：TU722文献标志码：A

基金项目：中国博士后科学基金资助项目（2017M622575），China Postdoctoral Science Foundation（2017M622575）

Optimization Algorithm for Resource Leveling of Construction Projects with Multiple Resources Based on Subset Simulation

WANG Jia1，2，LIU Kexin1，ZHANG Xueqing3，CHEN Tao4

（1. College of Civil Engineering，Hunan University，Changsha 410082，China；2. National Center for International Research Collaboration in Building Safety and Environment，Hunan University，Changsha 410082，China；3. Department of Civil and Environmental Engineering，Hong Kong University of Science and Technology，Hong Kong 999077，China；4. Changsha Midea Real Estate Development Co Ltd，Changsha 410082，China）

Abstract：In this paper，an efficient optimization algorithm based on subset simulation is proposed for solving the resource leveling problem of construction projects with multiple resources. In the resource leveling problem，if the de-cision variables are chosen to be the scheduled starting time for the involved activities，the logical relationship be-tween the activities may be violated during the implementation of the optimization algorithm. In order to avoid this problem，the interval rate variables are introduced to substitute the scheduled starting time in modeling the resource leveling problem of construction projects with multiple resources so as to simplify the procedures of the proposed opti-mization algorithm based on subset simulation. As shown in the illustrative example，compared with the widely used genetic algorithm，the proposed optimization algorithm can obtain higher improvement in the stability of achieving the optimal solution.

Key words：resource levelling problem；subset simulation；Markov chain Monte Carlo simulation；interval rate；genetic algorithm

建设项目的施工过程需消耗大量的人工、材料、机械等资源.如果建设项目实施过程中的资源计划（劳动力计划、材料进场计划、机械排班等）安排不合理，会引起建设项目工期内资源消耗量的过大波动（表现为施工人员的窝工或少工、材料和机械的过度使用或空置等），最终影响建设工程的生产效率、成本节约和项目管理质量[1].作为资源调度优化的手段之一，资源均衡问题（Resource Leveling Problem，RLP）旨在通过调整项目中非关键工序的计划开始时间，在不延长项目工期和不违反各工序间逻辑关系的前提下，降低项目工期内资源消耗量的波动.

针对资源均衡问题的研究工作可分为两类，一类偏重于资源均衡问题的模型构建，一类偏重于资源均衡问题的优化算法.资源均衡优化模型一般可归结为四类：简单的平方和模型[2-3]、考虑实际资源消耗量与期望值之间差值的偏差模型[1，4-5]、考虑不同周期资源消耗量变动的波动模型[6-7]、以及基于熵理论的熵模型[8-9].资源均衡问题的优化算法主要分为精确算法和启发式算法.其中，精确算法主要基于动态规划、整数规划、分支定界法等方法[10]，而启发式算法主要基于蚁群算法[11]、粒子群算法[12]、禁忌搜索算法[13]、遗传算法[14-18]等算法.资源均衡问题的复杂程度随涉及工序数量的增加而急速上升.因此，针对工序数量较多的项目资源均衡问题，精确算法并不适用，只能采用启发式算法.但是，启发式算法具有随机性，其每次运行获得的最优解不一定相同（不稳定），但现有启发式算法在最优解获取稳定性上仍有较大的改进空间.

本文针对建设工程项目的多资源均衡优化问题，提出一种基于子集模拟的启发式优化算法.同时，为避免工序间逻辑关系违反时复杂修复算子的使用，本文采用间隔率变量表示的建设工程项目多资源均衡优化模型，以简化基于子集模拟的优化算法的操作.通过算例验证，与应用较广的遗传算法相比，本文提出的优化算法在最优解获取稳定性上有较好的改进.

1建设工程项目多资源均衡优化模型

针对建设工程项目的多资源均衡优化问题，研究者一般借助网络计划工具进行分析，并在一定的假设下构建模型.本文研究的多资源均衡优化模型基于以下假设：

1）组成建设项目的各个工序必须连续施工，不能间断，且各工序间的逻辑关系不随时间改变.

2）组成建设项目的各个工序在实施期内，单位时间内耗费资源的种类和数量保持不变.

3）建设项目的总工期保持不变.

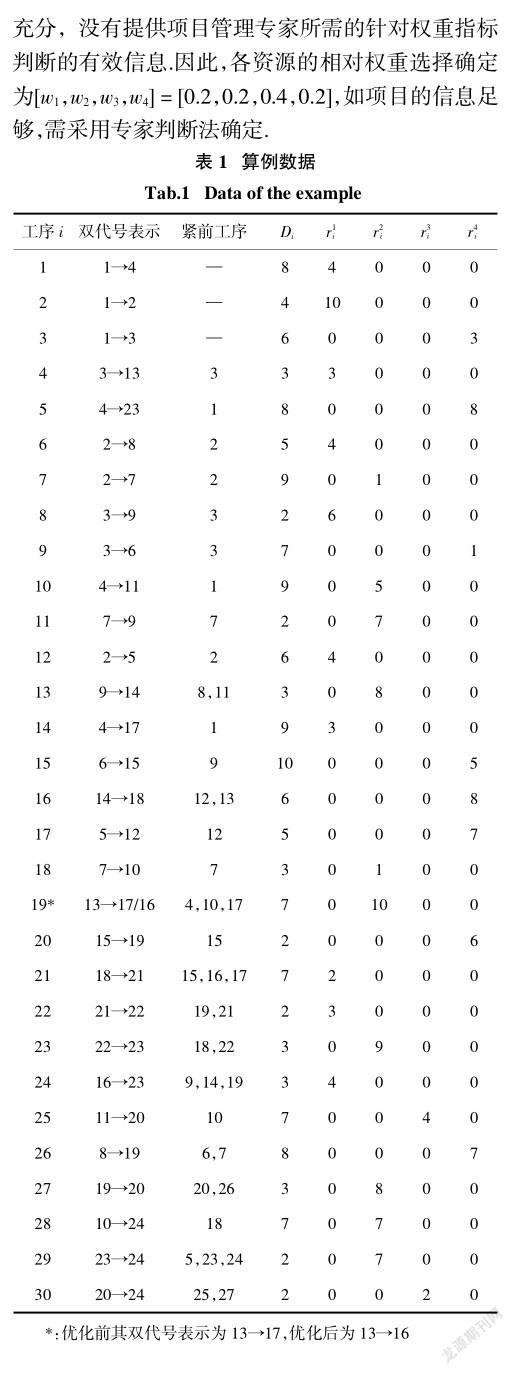
為检验基于子集模拟的多资源均衡优化算法的性能，每代随机抽样样本数量取M = 2 000，条件概率参数取p0= 0.1，改进Metropolis-Hasting方法中一维均匀概率分布的宽度取d = 0.3.图7描述了基于子集模拟的建议优化算法一次典型求解过程中，最优目标函数值随迭代阶段的变化.由图7可知，算法经过19代迭代后收敛到最优解，对应最优目标函数值1.115 4.该最优解对应的各工序计划开工时间Si如表2所示.为直观对比优化前后各工序的开工时间，图8和图9绘制了优化前后的双代号时标网络图，各工序在图中的双代号表示见表1第2列.

为检验基于子集模拟的建议优化算法的稳定性，表3给出了建议优化算法100次独立运行求解后的统计结果.目前，针对资源均衡问题的启发式算法间的对比研究较少，学界对各种启发式算法的优劣未达成共识.同时，遗传算法因其自行概率搜索、运算并行性、应用不依赖问题种类的强鲁棒性等特点，在资源均衡问题中应用更为广泛[16-18].因此，本文选择遗传算法进行对比分析，与其他启发式算法的对比分析，将在后续的研究中进行.表3提供了遗传算法（Genetic Algorithm，GA）100次独立运行求解后的统计结果.考虑到交叉概率参数pc和变异概率参数pm对GA算法求解的影响，本文依据两个参数的一般取值范围，进行了大量pc和pm组合取值下GA算法的性能检验.检验发现，交叉概率pc= 0.2和变异概率pm= 0.015下GA算法求解本算例多资源均衡问题的性能最优，因此表3给出的是这组交叉概率和变异概率下GA算法的对比结果.同时，考虑到计算资源对两种优化算法的影响，两种优化算法中每代的样本数均取2 000，迭代次数均取30代.

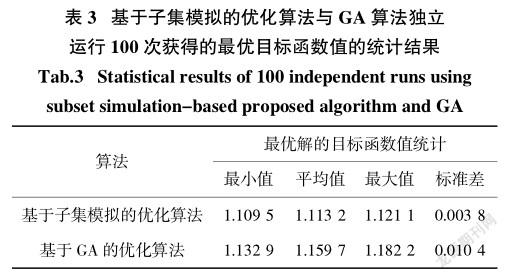
表3提供了两种算法100次独立运行求解获得的最优解的目标函数值的统计结果（最小值、平均值、最大值及标准差）.对比可知，基于子集模拟的优化算法获得最优目标函数值的平均值为1.113 2，小于基于GA的优化算法的相应数值（1.159 7）.同时，基于子集模拟的优化算法获得最优解的目标函数值的最大值（最差情况下）为1.121 1，小于基于GA的优化算法获得最优解的目标函数值的最小值（最好情况下）1.132 9，且最优目标函数值的标准差更小.此外，图10给出了两种算法100次独立运行获得的最优解的目标函数值的分布情况.由图10可见，基于子集模拟的优化算法性能更优，其获得的最优目标函数值更小，且分布更为集中，有93%的最优目标函数值集中在[1.109，1.119]区间，表明基于子集模拟的建议优化算法获取最优解的稳定性更高.

5结论

本文针对建设工程项目的多资源均衡优化问题，基于子集模拟法进行启发式优化算法的研究，主要研究结论如下：

1）在构造建设工程项目多资源均衡优化模型时，引入间隔率变量，并在间隔率变量和工序计划开始时间的映射中考虑工序间逻辑关系，以避免工序逻辑关系违反时复杂修复算子的使用.

2）针对间隔率变量表示的建设工程项目多资源均衡优化模型，提出基于子集模拟的建议优化算法，并给出算法框架和具体操作步骤.

3）通过算例验证，与应用较广的遗传算法相比，基于子集模拟的建议优化算法在最优解的获取稳定性上有较大改进.

参考文献

[1]EASA S M. Resource leveling in construction by optimization[J]. Journal of Construction Engineering and Management，1989，115（2）：302—316.

[2]HEGAZY T. Optimization of resource allocation and leveling using genetic algorithms[J]. Journal of Construction Engineering and Management，1999，125（3）：167—175.

[3]NEUMANN K，ZIMMERMANN J. Procedures for resource leveling and net present value problems in project scheduling with general temporal and resource constraints[J]. European Journal of Opera-tional Research，2000，127（2）：425—443.

[4]CHAN W T，CHUA D K H，KANNAN G. Construction resource scheduling with genetic algorithms[J]. Journal of Construction En-gineering and Management，1996，122（2）：125—132.

[5]AKPAN E O P. Resource smoothing：a cost minimization approach[J]. Production Planning & Control，2000，11（8）：775—780.

[6]SENOUCI A B，ELDIN N N. Use of genetic algorithms in resource scheduling of construction projects[J]. Journal of Construction En-gineering and Management，2004，130（6）：869—877.

[7]EL-RAYES K，JUN D H. Optimizing resource leveling in construc-tion projects[J]. Journal of Construction Engineering and Manage-ment，2009，135（11）：1172—1180.

[8]CHRISTODOULOU S E，ELLINAS G，MICHAELIDOU -KAME-NOU A. Minimum moment method for resource leveling using en-tropy maximization[J]. Journal of Construction Engineering and Management，2010，136（5）：518—527.

[9]QIAO J F，LI Y. Resource leveling using normalized entropy and relative entropy[J]. Automation in Construction，2018，87：263—272.

[10]李洪波，熊勵，刘寅斌.项目资源均衡研究综述[J].控制与决策，2015，30（5）：769—779. LI H B，XIONG L，LIU Y B. A literature survey of project resource leveling[J]. Control and Decision，2015，30（5）：769—779.（In Chinese）

[11]ALSAYEGH H，HARIGA M. Hybrid meta-heuristic methods for the multi-resource leveling problem with activity splitting[J]. Automa-tion in Construction，2012，27：89—98.

[12]ZHANG H X，YANG Z L. Accelerated particle swarm optimization to solve large-scale network plan optimization of resource-leveling with a fixed duration[J]. Mathematical Problems in Engineering，2018，2018：1—11.

[13]KOULINAS G K，ANAGNOSTOPOULOS K P. A new tabu searchbased hyper -heuristic algorithm for solving construction leveling problems with limited resource availabilities[J]. Automation in Construction，2013，31：169—175.

[14]LEU S S，YANG C H，HUANG J C. Resource leveling in construc-tion by genetic algorithm-based optimization and its decision sup-port system application[J]. Automation in Construction，2000，10（1）：27—41.

[15]PONZ-TIENDA J L，YEPES V，PELLICER E，et al. The Resource Leveling Problem with multiple resources using an adaptive genetic algorithm[J]. Automation in Construction，2013，29：161—172.

[16]歐阳红祥，陈伟伟，李欣.基于间隔率和遗传算法的多资源均衡优化研究[J].武汉理工大学学报（信息与管理工程版），2014，36（1）：82—85. OUYANG H X，CHEN W W，LI X. Leveling optimization of multipleresources based on interval rate and genetic algorithm[J]. Journal of Wuhan University of Technology（Information & Management Engi-neering），2014，36（1）：82—85.（In Chinese）

[17]LI H B，DEMEULEMEESTER E. A genetic algorithm for the robust resource leveling problem[J]. Journal of Scheduling，2016，19（1）：43—60.

[18]LI H B，XIONG L，LIU Y B，et al. An effective genetic algorithm for the resource levelling problem with generalised precedence relations[J]. International Journal of Production Research，2018，56（5）：2054—2075.

[19]何立华，王栎绮，张连营.多资源均衡优化中基于专家权重聚类的权重优选法[J].系统工程，2014，32（12）：124—132. HE L H，WANG L Q，ZHANG L Y.The weight optimal choice method based on experts’weights clustering analysis in multi-re-source leveling optimization[J].Systems Engineering，2014，32（12）：124—132.（In Chinese）

[20]AU S K，BECK J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Me-chanics，2001，16（4）：263—277.

[21]LI H S，AU S K. Design optimization using Subset Simulation algo-rithm[J].Structural Safety，2010，32（6）：384—392.

[22]朱俊杰，余雄庆.基于子集模拟优化的空天飞机再入轨迹混合优化方法[J].航天控制，2015，33（6）：51—56. ZHU J J，YU X Q. A hybrid optimization method for reentry trajecto-ry of space plane based on subset simulation optimization[J]. Aerospace Control，2015，33（6）：51—56.（In Chinese）

[23]KOLISCH R，SPRECHER A. PSPLIB - A project scheduling prob-lem library[J].European Journal of Operational Research，1997，96（1）：205—216.