追求平均数的统计味

朱孟迪

【摘   要】平均数作为一个统计量，是学生易学会用，但对其统计意义却难以理解的一个数学概念。就统计的意义而言，学习平均数是学生第一次接触“代表性”;就学生数感的发展而言，学习平均数意味着学生开始涉及虚拟数的理解。围绕“代表”与“虚拟”展开教学，可以帮助学生更全面地认识平均数，进而积累数据分析的相关经验。

【关键词】平均数;代表;虚拟;统计

一、现象篇——学生之现状

学生虽然没有学习过平均数，但经常与“平均分”打交道，不少学生已经能用“求和平均”计算一组数据的平均数。但当问及平均数是不是平均分时，许多学生果断地认为“是”。可见，学生头脑中的平均数与统计视角下的平均数是有偏差的。

（一）误把“平均数”等同于“平均分”

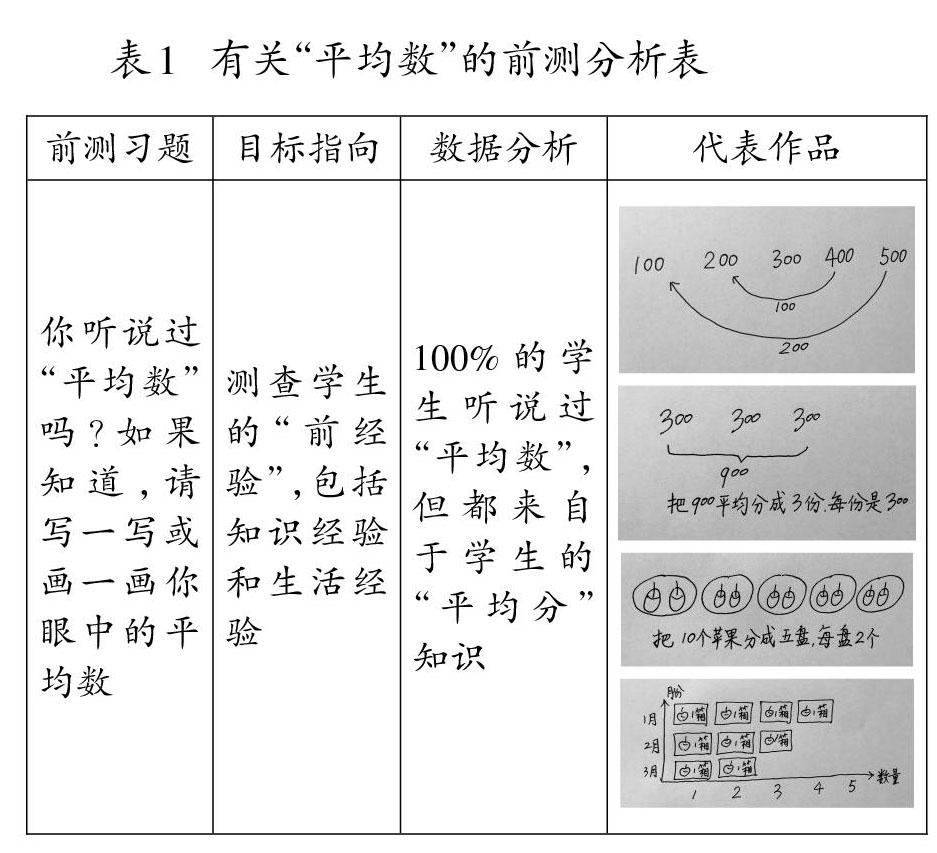
为了解学生的学习起点，上课之前，笔者对两个班65位学生进行了前测，结果分析如表1。

史宁中教授指出，平均数的概念有两个要点：第一，它代表一组数的整体水平。第二，它具有虚拟的特征。前测表明，学生简单地将“平均数”等同于“平均分”，这是对平均数的一种片面的理解。学生对平均数具有的“代表性”和“虚拟性”一无所知。

（二）误把“虚拟数”理解成“具体数”

为了解学生是否理解生活中的平均数，笔者设计了如下问题：“金湾小区有80户家庭，共有私家车120辆，平均每户家庭拥有1.5辆汽车。”看学生能否从以下两个维度来回答问题：（1）代表性——能不能说出1.5辆代表金湾小区汽车拥有的整体水平;（2）虚拟性——能不能说出1.5辆不是一个真实的数据，是因为计算得不到整数的结果。访谈中，许多学生不理解1.5辆的真正含义，最多只能这样解释：1.5辆表示“1辆半”汽车。

通过前测、访谈与分析，笔者认为平均数是学生易学会用，但对其统计意义却难以理解的一个数学概念——平均数代表一组数据的整体水平，是一个虚拟的数。

二、思考篇——学生之困因

（一）纵向——历史原因

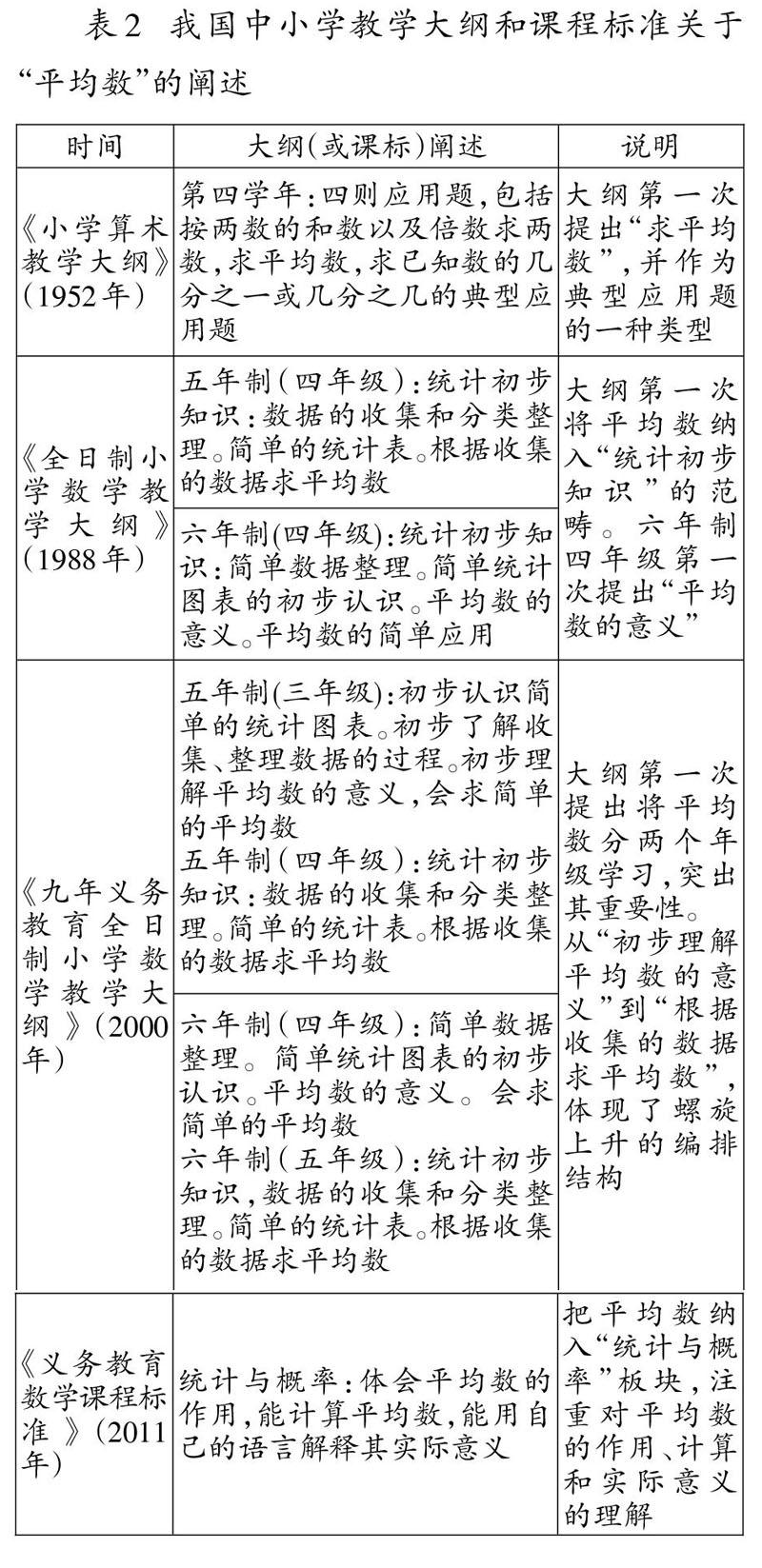
20世纪80年代以前，中小学数学课程中的平均数概念，常以典型应用题的形式呈现。随着时间的推移，平均数作为统计概念进入小学课程。表2是笔者查阅的我国中小学教学大纲和课程标准中有关“平均数”的阐述。

由此可见，在小学对平均数的教学，经历了纵横两个方向对算术平均数的深入。横的方向是指平均数思想的发展，从利用平均数估计总数，到重复测量取平均数减少误差，发展为平均数作为总体的代表值，实现了代数概念到统计概念的飞跃。因此，人们对平均数的认识，受着历史的影响。

（二）横向——教材原因

现行教材的编排是否基于“统计视角”呢？笔者查找了四套教材对“平均数的定义”，进行了整理对比（见表3）。

小学教材对平均数的定义以“描述性”居多，人教版、北师大版则关注“用哪个数字代表这组数据”的“找代表”的过程，有些教材还只停留在“算法理解”的层面上，没有上升到“统计理解”的层次。这给学生真正领会平均数的统计意义带来不利影响。

三、实践篇——学生之体验

平均数的教学应该包含以下内容：平均数的概念及蕴含的方法与应用;平均数的计算：总数除以总份数或者移多补少;平均数可以代表整体水平，可以用来比较两组数的水平，具有统计价值。

（一）自主探索，“交流质疑”论虚拟

学生常以“超常发挥、正常发挥、失常发挥”来描述比赛。那么，如何判定是正常发挥呢？这就需要用一个数来代表一组数据，平均数的“代表性”就体现出来了;如果这个数没有出来呢？平均数的“虚拟性”就呈现出来了。

【教学片段1】感知代表，初识虚拟

师：同学们请看，小红在踢毽子，这时体育老师走过来问她：“小红，你踢毽子的水平怎样？”小红看了看自己五次的成绩，想：我该用哪个数来代表这五次踢毽子的水平？又该怎么回答老师呢？如果你是小红，会怎么说？为什么？

生：5个，因为5出现了两次。

生：6个，因为6是平均数。

师：可是6个没踢出来，那不是骗人吗？

生：她有这个水平，这是她的正常水平。

生：虽然这5次没有踢出来，但这不代表她下一次踢不出来。

师：是呀！小红的水平摆在那里，下一次很有可能踢出的个数就是6个。

学生围绕“小红该用哪个数代表这五次踢毽子的水平”展开讨论与辨析，可以突出平均數的代表性。学生凭借自己的生活经验，能想到用“最大数或最小数”来代表不合适，于是就会从5，6，7中选一个代表。选择代表的过程，就是不断辨析的过程。很多学生能借助“计算经验”得到6个最合适。但“6”没有踢出来，却要用它来代表这一组数据的水平，显然需要有更“合理的解释”。此时，平均数“推断分析”的功能就显现出来了——下一次很有可能踢出的个数就是6个。

（二）借助起点，“自主探究”展虚拟

平均数是一个“虚拟”的数，所以平均数的获得需要总数除以总份数或者移多补少。笔者通过前测与访谈知道多数学生能运用这两种方法。因此，可借助学生的自主探究，展示这个虚拟数的“获得”过程。

【教学片段2】基于起点，探究虚拟

教师把小红五次踢毽子的结果制作成统计图。请学生在图上圈一圈，画一画，也可以写一写，算一算，表示自己的想法。学生独立思考、探究。先完成的学生可与其他同学交流，接着全班进行交流。

生：（移多补少）把比6多的那些移给比6少的，不多不少，刚刚好。

生：（求和平均）（5+4+7+5+9）÷5=6。

实践表明，学生能借助“移多补少”与“求和平均”来得到平均数这个“虚拟数”，通过同伴互助与讲解，一些不会的学生也能很快领会这两种方法。该过程很好地建立了平均数与平均分之间的联系。

（三）数形结合，“变与不变”议虚拟

在教学中，应把抽象、静态的数学问题设计成有形的活动。统计图表的灵活使用能使学生的学习事半功倍。

【教学片段3】在“对比”中理解平均数的虚拟性

师：同学们请看（如右图），这儿有7，这儿也有7，你认为这两个7的意思一样吗？为什么？

生：一个是李雷真实的踢毽个数，一个是平均数。

师：看来，平均数与真实的数会有差别，所以，它常常借助这样一条虚线。

将平均数与某个真实数据相对比，学生可以更客观地认识平均数，感受平均数代表一组数据的“整体水平”，它是“移多补少”或是“求和平均”的结果。因此，它跟组内每一个数据都有密切的关系，它能代表一组数据的整体水平。

【教学片段4】在“数据变化”中理解平均数的虚拟性

师：（课件出示如下图组）请看男生队的成绩。如果谢明明的成绩变成了10个，你认为平均数会变吗？怎么变？

生：（10+4+7+8+11）÷5=8。

生：10-5=5，5÷5=1，7+1=8。

师：看来，求平均数的方法还不止一种呀。如果刘东的成绩变成6个，你又想到了什么？

……

小结：经过这两次变化，你对平均数想说什么吗？

生：只要一个数发生变化，平均数也会变化。

师：是呀，平均数非常敏感，会随着某个数的变化而变化。如果再加一个同学陈明，相信平均数也会发生变化吧（出示7个）。平均数变了吗？为什么又不变了呢？由此你想到了什么？

生：如果增加的數量与平均数同样多，总的平均数还是不变的。

师：哦，原来如此。看来，变与不变还需要我们认真地分析数据呀。

平均数是进行统计分析和统计推断时最常用、最主要的集中量数。实践表明，学生理解平均数的敏感性、虚拟性并非易事。平均数的敏感性导致它易受极端数据的影响。教学中，直观图的呈现让数据的变化更形象，透过平均数线的上下波动，学生在变与不变中再一次感悟平均数的虚拟性。

【教学片段5】借助小数，深化对平均数虚拟性的感悟

师：要是孙奇从4个变为5个，你觉得平均数会变吗？

生：会变，变成7.2。

师：难道踢毽子的个数会是小数？有这么稀奇的事情吗？

师：7.2个是他、是他（指名字）的吗？那平均数代表的是什么？（整体水平）是呀，正因为这个平均数是我们算出来、想出来的，它代表这一组数据的整体水平，并不代表某个同学的踢毽个数，所以出现小数是正常的。

师：这让我想到了一条曾让我感到稀奇的信息。读一读这条信息：金湾小区住着80户家庭，共有私家车120辆，平均每户家庭拥有1.5辆汽车。现在，你会怎样理解它？

生：1.5辆是金湾小区每户家庭私家车拥有量的代表。

生：这个1.5辆不是真实的车辆，是算出来的，想出来的……

创设平均数是小数的情境，划清虚拟数与真实数的界线，有利于学生加深对平均数虚拟性的理解。从实践效果来看，学生对平均数的代表性与虚拟性的理解比较到位，能站在统计的视角分析数据、处理数据，进而更准确地描述生活现象。

教学“平均数”，应该引导学生站在统计的视角认识与理解平均数，帮助他们积累数据分析的相关经验，不应该囿于怎样计算平均数。透视“代表”与“虚拟”，可发现学生之“难”;诠释“代表”与“虚拟”，可解学生之“难”。只有透析平均数的代表性与虚拟性，才能彰显平均数的统计味。

参考文献：

[1] 课程教材研究所.20世纪中国中小学课程标准·教学大纲汇编：数学卷[M].北京：人民教育出版社，2001.

[2]陈希孺.数理统计学简史[M].长沙：湖南教育出版社，2002.

[3]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

（浙江省慈溪市崇寿镇中心小学   315300）