利用激光超声纵波的衍射信号测量开口裂纹
宋 艳,马世榜
(1.郑州信息科技职业学院,河南 郑州 450001;2.南阳师范学院机电工程学院,河南 南阳 473061)
1 引 言
零部件在制造或使用过程中,不可避免地存在着浅表裂纹和应力集中[1],随着服役时间的增加,浅表裂纹扩展至材料表面逐渐形成开口裂纹。人们迫切希望测量出开口裂纹的参数,以便作为修复后继续使用或者直接判废的依据。作为一种超声波的非接触式激励方法,激光超声激励技术在工业生产中得到不断推广[2]。激光超声检测中,表面裂纹的测量大多基于表面波来实现,吴瑞等[3]利用反射回波的震荡时间差评估金属表面微裂纹深度。徐志祥等[4]模拟了热弹机制下表面波与裂纹的作用过程,获得了表面波时域特征与表面裂纹深度之间的关系。杨连杰等[5]讨论了一定缺陷深度范围内,反射系数和透射系数与缺陷深度呈近似的关系。黄燕杰等[6]模拟了激光激发的表面波与材料表面缺陷的相互作用过程,通过反射瑞丽波的幅值变化判断缺陷的深度,此外,秦峰等[7]还根据能量衰减值判断裂纹深度。除了利用激光超声表面波检测表面裂纹以外,王玉庆等[8]还分析了利用横波测量裂纹参数的方法。然而,尚未见到利用激光超声纵波测量表面裂纹的公开文献。
在工件内部,烧蚀机制激励出的纵波声场具有朝各个方向均有分布的特征,使得利用纵波测量开口裂纹成为了可能。本文基于纵波声场指向性,分析了纵波在开口裂纹处可能衍射出的信号成分,讨论了利用纵波开口裂纹的衍射信号测量裂纹的方法。对于衍射出的纵波信号,分析了相位特征和渡越时间的特点,并推导出裂纹参数的计算公式,最后进行了仿真分析及实验验证。
2 纵波声场特征及衍射信号特性
金属工件的材料密度为r,汽化潜热为L,材料的比热为Cp,汽化温度和初始温度分别为Tv和T0,表面吸收率为A,在功率密度为I的脉冲激光烧蚀下,等离子体对工件表面的反冲压力σ为[9]:
(1)
圆光斑易于实现且其参数便于调节,因此在激光超声检测过程中常常使用圆光斑进行超声波的激励。半径为R的脉冲激光光斑激励出的纵波声场指向性为[10]:
D(θ)=
(2)
式中,θ为工件内部纵波声场中的质点与圆光斑中心的连线相对于工件内法线的夹角;k表示纵波速度与横波速度的比值;c,f分别为纵波的速度及中心频率;J1则是第一类第一阶贝塞尔函数。
从式(2)中可知,激光光斑的半径R及纵波的中心频率f影响着纵波声场的指向性。图1中为几种典型参数下的纵波声场指向性图形,考察中心频率f一定的纵波声场,光斑半径R越小,声场能量就越发散,如图1(a)所示;图1(b)则表示光斑半径R相同时,纵波信号的中心频率f越低,声场能量分布越发散。欲使用纵波测量工件表层附近的裂纹参数,应该选用合适的参数组合,以保证纵波能量到达裂纹的尖端。
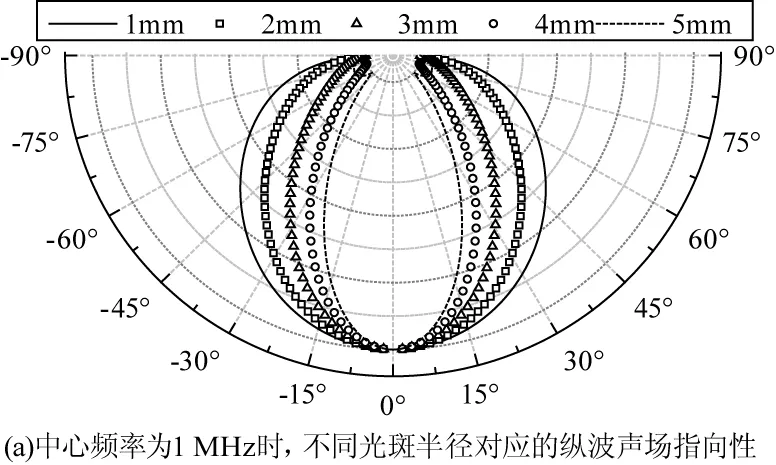
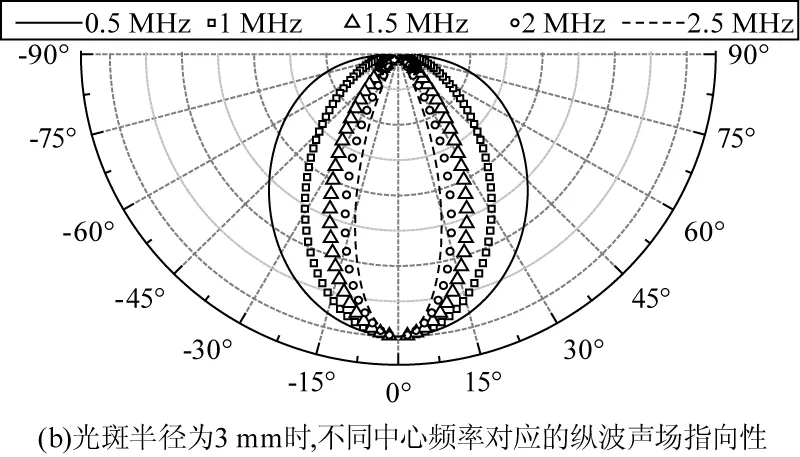
图1 纵波声场指向性图形
工件中的超声波在传播过程中,遇到裂纹尖端会发生衍射,并伴随着波形转换。为便于标识,将纵波记作P(压力波,pressure wave),横波记作S(剪切波shear wave)。其中,衍射后仍以纵波的形式继续传播的部分记作PtP,衍射后以横波的形式继续传播的部分记作PtS。两种信号均可在裂纹另一侧的表面上被接收到,如图2所示。 固体材料中,纵波速度大于横波速度,而横波速度又大于表面波速度。表面波仅沿工件表面(包括裂纹表面)传播且其声程最大,因此,PtP最先到达C点。
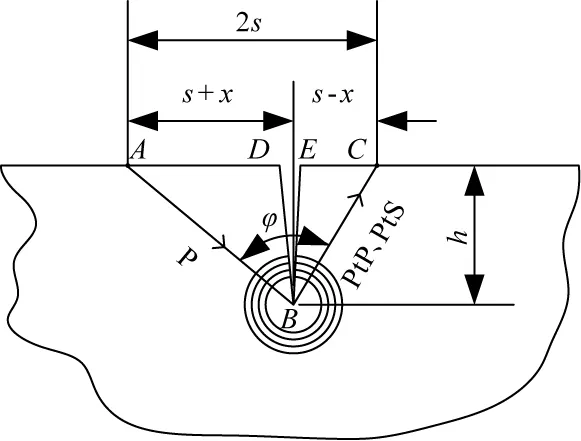
图2 纵波在裂纹尖端发生衍射
图2中,激励源中心-检测点的距离为2s,裂纹尖端的深度为h,设裂纹尖端的水平位置与激励-检测点中心的距离为x,则PtP的渡越时间为:
(3)
当x=0时,t取得最小值。实际测量时,在固定激励-检测点距离的前提下,可根据这一特征,寻找出裂纹尖端对应的水平位置。同样地,测得裂纹尖端水平位置处于激励源中心-检测点中心时的渡越时间t0后,便可求出裂纹深度h。
(4)
衍射纵波信号除了具有上述的时间特征之外,还具有首波相位反转的特征[11]。定义激励源中心同裂纹尖端的连线与激励源中心同裂纹尖端的连线之间的夹角为回折角φ(见图2所示),回折角的临界值为φ0,φ>φ0时PtP的相位与φ<φ0时PtP的相位相反。回折角临界值φ0与固体材料的泊松比μ相关。常用金属如碳钢、铝及铜的泊松比的范围为0.24~0.33,对文献[11]中的数据进行多项式插值得到表1中的数据。在开口裂纹的测量过程中,可根据相位反转的特征判断出衍射纵波。

表1 回折角的临界值
较浅开口裂纹的缺陷信号可能会隐藏在掠面纵波中[12],导致无法识别,因此还存在着一定的盲区深度,其计算公式为[13]:
(5)
式中,Dds表示盲区深度;tp为直通波脉冲时间,本文中取2个周期,即2/f,其余参数含义同上。
3 模拟分析及实验验证
为了便于分析对比,对含有开口裂纹工件进行参数化建模,图3为相应的二维有限元模型,A、C分别为激励源中心和接收点。裂纹尖端在水平方向上的投影与AC的中点重合,并以此处为原点建立直角坐标系。工件的长度、高度分别为L、H,A点坐标及B点坐标分别为(-s,0)和(s,0),裂纹深度为h。工件的底部设置为固定约束,为了防止左右边界反射产生干扰,则将相应边界设置为吸收边界,其余边界则为自由边界。选用三角形的平面单元离散模型,网格大小设置为最小波长的1/8[14],时间积分步长则为1/(20 f)。考虑激光烧蚀材料产生的反冲压力σ在区域[-s-R,-s+R]内以中心频率f施加于工件的表面,其等效载荷的表达式为[15]:
P(t)=

(6)
对整个模型进行瞬态分析,可在C点获得裂纹尖端的衍射信号。

图3 工件的有限元模型
取中心频率为f=2.5 MHz,工件材料为铝时,其密度、泊松比、纵波速度分别取以下数值:2700 kg/m3、0.34、6300 m/s。另外取s=10 mm,h=8 mm,图4(a)为某时刻的声场快照,可在开口裂纹的尖端附近观察到衍射纵波。图4(b)为C点接收到的超声波信号,矩形框中为衍射纵波,其到达时间为4.06 μs,与理论值4.065 μs相符。当材料为碳钢时,其密度、泊松比及纵波速度分别为7800 kg/m3、0.285、5900 m/s,根据表1求出回折角临界值φ0=78°。依次取开口裂纹深度为8 mm和15 mm,它们所对应的回折角分别为103°和67°。在C点处接收到的超声信号分别如图4(c)、图4(d)所示,对于深8 mm的开口裂纹,衍射纵波的渡越时间为4.305 μs;而对于深15 mm的开口裂纹,衍射纵波的渡越时间则为6.105 μs。根据公式(4),求出开口裂纹深度的模拟计算结果分别为7.83 mm与14.98 mm,均与有限元模型中的裂纹深度相接近。另外,图4(c)与图4(d)还验证了当回折角跨过临界值时,衍射纵波具有相位反转的特征。

搭建基于烧蚀机制的开口裂纹激光超声测量实验系统,脉冲激光的参数为:脉冲宽度8 ns,波长1064 nm,单脉冲能量40 mJ,脉冲激光经由聚焦透镜后形成圆光斑会聚于工件表面。使用中心频率为2.5 MHz的纵波探头接收信号,触发信号由脉冲激光器的控制系统提供,使用示波器显示和存储数据。采用相同参数的激光辐照在黑色相纸上,获取10个不同位置处的光斑烧蚀痕迹,利用工具显微镜测量出每个烧蚀圆斑的直径,然后求出平均值为2 mm。根据上述参数,求得辐照在试样表面的激光功率密度为1.59×108W/cm2,高于铝产生明显烧蚀的实验值[16]1.25×108W/cm2。此时,烧蚀导致的喷溅物质作用于工件表面,产生纵波、横波及表面波。
利用线切割在铝质试样上加工出的开口裂纹深度分别为10 mm,20 mm。对于10 mm深的开口裂纹,当s=12 mm时,据式(5)求出最大盲区深度为8.2 mm,即所选的s值满足测量要求。测得的时域信号如同图5(b)所示,纵波的到达时间为4.90 μs,根据公式(4)求得深度值为9.7 mm。对于深度为20 mm的裂纹,当s=14 mm与s=22 mm时,最大盲区深度为10.8 mm,s值同样均满足测量要求。两种s值下,测得的信号分别如图5(c)及图5(d)所示,对应的纵波到达时间为7.78 μs和9.53 μs,依照式(4)求出的裂纹深度值为20.1 mm,20.4 mm,求得测量平均值为20.25 mm。

根据上述两个开口裂纹实际值与测量值,可知测量误差分别为-3 %与1.3 %。另外,对于深度为20 mm的开口裂纹,根据回折角临界值求得s的临界值s0=16.2 mm。因为测量中采用的两个s值恰好处于s0的两侧,所以在图5(c)及图5(d)中还呈现出衍射纵波具有的相位反转特征。
4 结 论
基于烧蚀机制的激光超声纵波声场指向性,针对开口裂纹,提出了利用衍射纵波测量开口裂纹参数的检测方法,并推导了裂纹深度的计算公式。在相同的激励-接收间距下,当激励源中心与接收位置的中心关于裂纹尖端呈两侧对称分布时,衍射纵波的渡越时间达到最小。另外,衍射纵波还具有相位反转的特征,可根据上述特征识别激光超声衍射纵波信号。最后,进行了有限元模拟分析及实验验证,结果证明开口裂纹深度的测量值与实际值之间的相对误差在5 %之内,可满足工程检测需求。

