改进线性PID算法的直流电机控制

中国兵器工业第214研究所 姜 峰 李 亮 曹 彪

直流电机和步进电机的运行特点不同，通过设置步进电机的运转步数来控制转过的角度，而直流电机不能直接精确地实现旋转角度的控制。通常会将电位计和直流电机配合使用，电位计的电位值和电机旋转角度是一一映射关系，通过采集指示直流电机旋转角度的电位值反馈控制直流电机旋转的角度。处理器选择TI的DSP的2000系列处理器TMS320F28335。

如果将DSP输出PWM波作为输入，将电机转动角速度作为响应，那么可以认为电机的转速和方向受PWM波的占空比影响，如果输出的PWM波的占空比为50%，则电机停转；当PWM波占空比大于50%时，电机会沿着某一个方向旋转，此时设这个方向为正方向，而当PWM波占空比小于50%时，电机会沿着反方向旋转，此时称电机反转，而且实验指出占空比和电机的转速呈现线性关系。

通常电机控制采用PID控制算法，PID控制是比例积分微分控制的缩写，直流电机的反馈控制算法采取改进线性算法的方案，改进算法的收敛速度优于线性算法，最后会给出改进算法和线性算法的对比结果。

1 线性算法

线性PID算法结构简单灵活，实用性好，在线性连续控制系统中得到广泛地应用。线性PID算法的模型不再赘述，直接切入正题。

图1 线性反馈算法和非线性反馈算法仿真图

图2 线性反馈算法和改进算法仿真图

设电机当前的角速度为ω[n]，电机从0时刻到目前所转过的角度为θ[n]，时间片为ΔT，即可得：

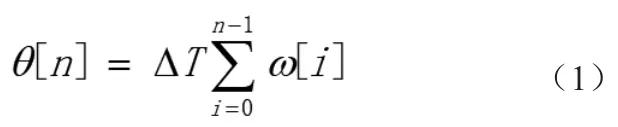
设直流电机待旋转的目标角度为θd，则可令：

又因为占空比和角速度之间呈现线性关系，且直流电机的角度位置和电位之间也呈线性关系，可分别记为：

其中V为电位计指示电压，Ω为PWM波占空比，所以上式可以写成：

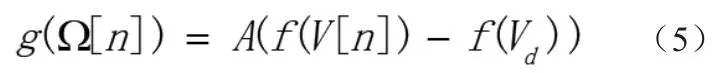
因为（2）（3）（4）均为线性关系，所以（5）可以写成如下形式：

即（6）可以写为：

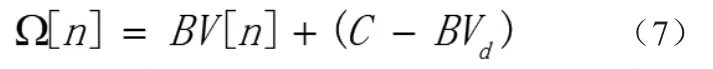
现已知当某一时刻采集的电位值V[n]=Vd时，Ω[n]应等于50%，即可得：

因为此系统为一个因果系统，假设零时刻之前的没有任何激励，则：

u[n]为阶跃信号，则可得（9）的系统冲激响应为：

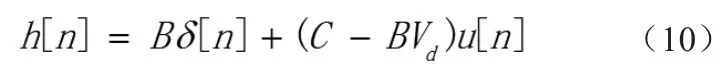
δ[n]为冲激信号，（10）的Z变换为：

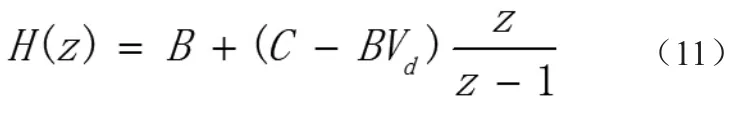
图3 软件流程图

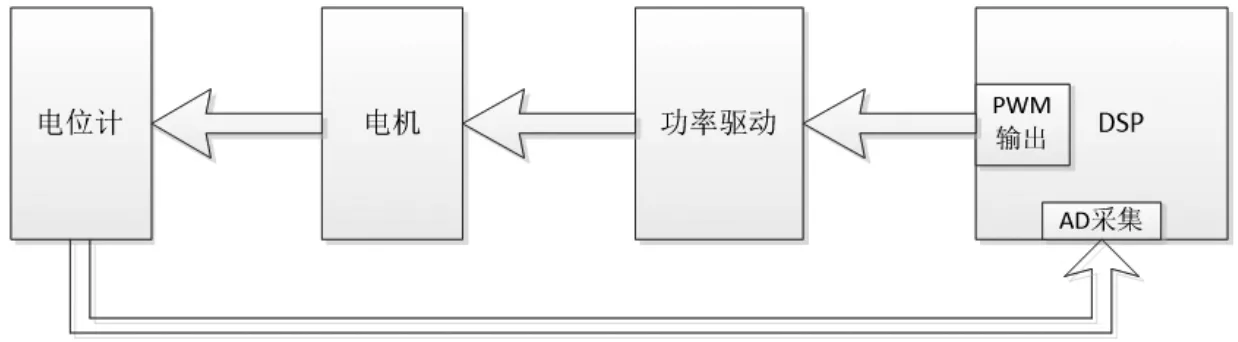
图4 系统硬件连接框图

由（12）即可得到：

由（7）和（13）可得PWM占空比和采集的反馈电位的函数关系：

2 改进线性算法

由（14）可知，采集的反馈电位与指示目标角度的电位相差越大，则DSP输出PWM的占空比就越远离50%。若为了使系统尽快收敛，当采集的反馈电位落在目标电位附近时，PWM占空比能够快速变化，以至于其在目标电位处的导数为无穷；否则PWM波的占空比应尽量远离50%，以使得电机能迅速转向目标角度，正是基于这样的考虑，根据常数变易法的思路，构建函数（15）：

图1为线性反馈算法与非线性反馈算法的仿真对比图，从仿真结果可以看出非线性反馈算法的收敛速度明显优于线性反馈算法，横坐标为时间轴，纵坐标为电机转过的角度，仿真设定的目标角度分别为5°、10°、15°、25°。但是非线性算法并不会稳定，而是振荡的，这样会导致电机不会停下来，而是不停地调整位置，这显然不是想要的结果。

图2为线性算法与改进算法的仿真对比图，从仿真结果上看，改进后的算法继承了非线性算法的收敛优势，而且不会产生振荡，可以使电机迅速转至目标角度。

从图2可以看出，当需要转过的角度很小（小于5°）时，基于改进的线性算法和线性算法反馈控制电机转过该角度的时间几乎一致；随着待转的目标角度增加，改进的线性算法达到目标角度的时间明显快于线性算法。

3 软硬件实现

图3为DSP实现直流电机控制的程序流程图，其中V1和V2为阈值电压，如果落在这两个电压之间仍旧采用线性算法，如果落在这两个电压之外，那么就采用非线性算法。

系统的硬件连接框图如图4所示。

总结：通过理论分析和仿真可知，改进反馈控制算法相较于线性算法而言，电机转动到目标位置的时间会有一定缩减，并且转过的目标角度越大，改进算法的优势就越明显。需要注意的是，非线性算法会导致运算速度增加，对DSP处理器的压力会有所增加。