Lasso-Cox模型在个人信用风险评估中的应用

李淑锦，嵇晓佳

（杭州电子科技大学 经济学院，浙江 杭州310018）

1 文献综述

国内外学者关于信用风险评估的研究主要集中于探讨影响借贷违约行为的因素、风险评估的模型选择及应用方面。

在个人借贷违约行为的影响因素研究方面，学者们发现有内外部因素之分，也可以表现为硬信息和软信息两个方面。傅彦铭、臧敦刚、戚名钰［1］基于借款人的信用等级、申请的贷款金额、期限、利率、收入等因素研究了对个人借款者信用风险的影响；李思瑶、王积田、柳立超［2］则考虑借款者的信用等级、收入水平、学历和所处地区等因素对个人借款者违约的影响；李延喜、孙大同、赛骞［3］基于个人借款者的特征，如年龄、学历、借款金额等指标来判别其是否会影响违约的风险；王浩名、马树才［4］通过对借款人的信用等级、FICO 分数等级、负债与收入比等因素研究了对违约概率的影响；王冬一、华迎、朱峻萱［5］在个人财务状况、房产车产、收入、学历等基本信息的基础上，加入社会关系来动态评估个人借款者的违约风险。除借款者个人特征，信用等级等方面数据会包含一些信用风险信息，借款者的消费行为和宏观层面因素也会对其违约行为产生影响。王正位、周从意、廖理等［6］研究表明，高频的消费行为所蕴含的信息能提高对借款者风险的识别效率；迟国泰、张亚京、石宝峰［7］研究发现，宏观经济因素对个体借款者的还款情况存在影响，实证结果表明景气指数、居民消费价格指数、城市人均可支配收入对其未来违约状态的影响是显著的。

在信用风险评估模型研究方面，有静态和动态模型之分，代表性的静态评估模型包括判别分析法和Logistic 回归方法等。如，方匡南、章贵军、张惠颖［8］研究发现，Logistic 回归模型在我国信用风险研究中具有更强的应用性和一定的代表性。SVM、随机森林、BP 神经网络、决策树［9-12］等静态评估模型也被运用到信用风险研究中，并取得了一定的研究成果。静态评估模型只能分析借款者在特定时间段内的违约概率，不能评估特定时点上的违约风险，而动态评估模型却可以。最常用的动态评估模型是生存分析模型，其中最具代表性的是成比例Cox 模型。Narain B［13］第一次将生存分析方法运用到信用评估中；Banasik J、Crook J N、Thomas L C［14］在前人研究的基础上发现，普通的静态评估模型如Logistic 回归与Cox 方法相比具有很好的评估效果；Stepanova M、Thomas L C［15］运用Cox模型预测了个人借款者的违约概率；邓丽纯、杜伟勇［16］运用Cox 模型预测了上市公司财务危机；刘忻梅、丁研、段羽中［17］运用Cox PH模型筛选了影响上市公司信用风险的财务指标。

综上所述，在个人借款者的信用风险评估中，最重要的是建立信用风险评估指标体系和选择合适的评估方法，学者们在研究过程中主要使用Logistic、SVM、决策树等静态方法进行实证研究。这些模型各有优缺点，如Logistic回归模型是较为经典的一个传统预测模型，具有高稳定性、高可解释性、建模难度低的特点，但导致欠拟合现象；SVM 适用小样本，且能处理非线性模型，但对大样本处理结果较差，且稳定性较低；决策树作为大数据处理问题的一个新模型，具有预测精度高、数据要求低、概率图解释清晰的特点，但也具有稳定性差，且仅用于离散变量的特性。这些静态方法的缺点是只能判别个人借款者在一定的期限内是否违约，却无法评估借款者什么时候违约。

本文的研究目的在于不仅发现影响个人借款者违约的重要影响因素，而且同时定量分析个人借款者在什么时刻违约。与传统的静态评估方法相比较，生存分析方法具有两个方面优势：一是生存分析可有效利用删失（Censored，本文特指在研究期间未发生违约的样本）数据；二是扩展的生存分析模型可纳入时间变量，且预估每个时点个人借款者违约的可能性。

从学者们的研究中可以发现，在评估个人借款违约时，选取的评估指标会对最终的评估结果产生很大的影响。在众多的特征信息中如何筛选出准确的、能反映个人信用风险的有效指标，成为建立信用风险评估指标体系的关键所在。常用的筛选方法有主成分分析法、Lasso方法等。方匡南、章贵军、张惠颖［8］研究表明，Lasso方法筛选的预测变量较向前逐步回归和向后逐步回归法都能获得更好的预测结果，因此本文拟采用Lasso方法建立有效的个人借款者信用风险的评估指标。

向晖［18］曾将单一模型和混合模型进行对比，发现混合模型的预测精度、稳健性、解释性等均优于单一模型。Lasso 和生存分析模型的特点具有以下两个特点：一是Lasso和生存分析模型具有一定的互补性，生存分析易造成欠拟合问题，而Lasso 正好能解决多重共线性和拟合问题；二是两个模型都可以解决非线性问题，且二者对数据的假设要求条件均较低。因此，将Lasso和生存分析模型相结合构建新的评估方法，可大大提高模型的预测精度和模型的整体可解释性，为信用评估模型和评估指标的运用提供了新思路。

2 研究方法

2.1 Cox 模型

生存分析常被用于医学实验中不同变量对被研究个体生存状态的影响，也就是在变量发生变化时，对个体生存时间的影响。信用风险研究中，生存状态的转变主要依据借款者是否发生违约，因此“T”特指从借款者完成借款的时间起点到发生违约事件所经历的月数。通常事件的生存特征由生存函数、危险函数和概率密度函数体现，本文运用生存分析方法研究在一定时期内借款者违约的影响因素，并给出相应的风险函数和风险概率，以发现个人借款者的“生存特征”。

生存函数：生存函数又称“累计生存率”，是指在t时刻企业个体的累计存活概率，一般用函数S（t）表示，数学形式为：

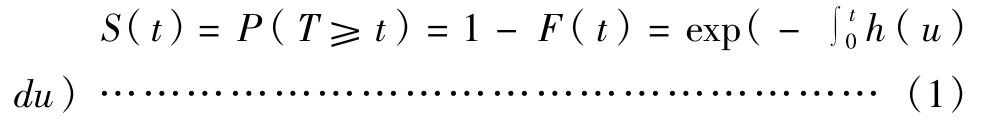
式中，T为个人借款者从筹资成功到发生违约情况所经历的月数；F（t）指个体生存时间T 的分布函数。

f（t）为概率密度，通常被用来衡量某个随机变量在任意一个确定的时间点附近取值的可能性，函数表达式为：

h（t）为危险函数，又被称为“风险函数”，是指个体在t时刻是未违约的，但在下一瞬间t+Δt（Δt→0）会发生违约的可能性，采用危险函数h（t）表示：

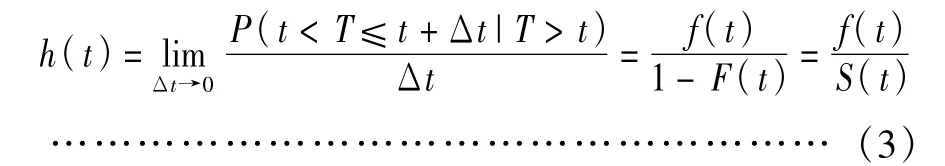
由定义可知，生存函数S（t）和危险函数h（t）可以转换，计算公式为：

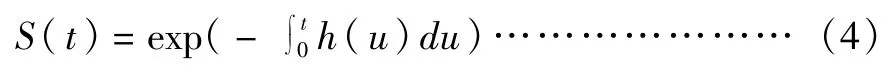
生存分析中有各种风险函数表示方法，本文主要采用Cox 模型。Cox 模型为半参数模型，模型中有一部分的结构是已知的，需要估计参数，而另外一部分结构未知。因此，Cox 模型一部分取决于估计的β值，另一部分则由依据时间t，但与协变量无关的基础风险函数h0（t）决定，表达式为：

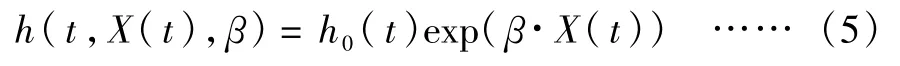
式中，h0（t）为基准风险函数，是指当解释变量为0 时个人借款者发生违约风险的概率；X（t）是包含了以下元素的解释变量：m个借款人特征指标x1，x2，…，xm，包括基本情况、工作情况、资产情况和信用情况；n个借款信息xm+1，xm+2，…，xm+n指标，这些指标是不随时间变化的；s 个动态的宏观经济指标y1（t），y2（t），…，ys（t），这些指标是动态的，为时间依存变量，随着时间变化而变化。本文中，若协变量不考虑宏观经济指标，该模型是Cox PH 模型；若协变量考虑宏观经济指标yi（t），则该模型就是扩展Cox模型。β1，β2，…，βp是模型通过极大似然函数和训练集数据估计得出的回归系数［19］：

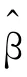
因此，每个借款人在任何时刻，以及任何一段时间的违约概率可以通过公式（1）和（5）获得［21］。

Cox模型参数估计中带有惩罚项的偏似然函数形式如下：

式中，ln（β）为扩展的Cox 模型的对数偏似然函数。

2.2 Lasso - Cox模型

由于大数据具有数据量大、存在冗余变量的特点，因此本文首先采用基于偏似然估计原理的Lasso方法对借款者违约的评估指标进行筛选。首先，充分考虑各自变量与因变量之间的关系，合理界定信用风险评估指标对因变量是否存在显著影响；然后，基于所选出的特征自变量利用扩展的Cox 预测进行预测，定量分析个人借款者的违约特征。

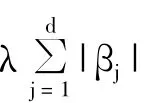
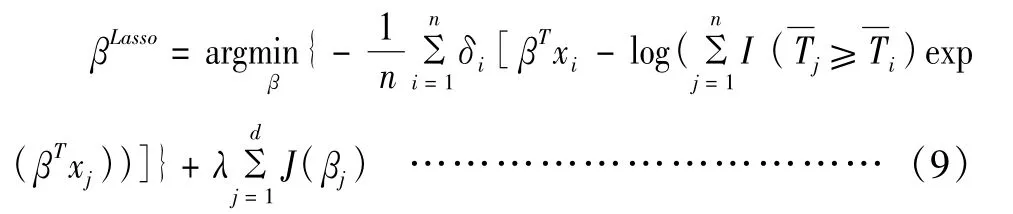
为提高变量选择的效果，需对λ参数进行调整，本文采用十折交叉验证方法来确定调和参数λ。交叉验证法首先把数据分成数量大致相等的K 份，对于第k份数据，用其他K - 1 份的数据拟合模型fk，然后计算当fk用于预测第k 份数据时的预测误差。令k ＝1，2，…，K，重复上述过程，最后汇总K 个模型的预测误差。实践中常令K ＝10，即十折交叉验证。十折交叉验证的预测误差表示为：

式中，k（i）是表示N 个样本中观测i 属于第k（k ＝1，2，…，K）份数据的指示函数；fk表示使用剔除第k份数据后拟合的模型。

假定拟合了一组含有调和参数的模型表示为fk（x，λ），定义为：

那么，CV（f，λ）就是一条随λ的变化而变化的检验误差曲线，找到使其最小的λ，就是Lasso- Cox 回归模型的调和参数：

在经过十折交叉验证得出估计的^λ值后，根据公式（9）得出βLasso的估计值，根据公式（5）得出被观察样本在t时刻发生违约的概率，即：

3 评估指标选择及数据来源

3.1 评估指标选择

李杰、刘露、Chao - Hsien Chu［24］对个人信用风险的研究发现，个人借款者的基本情况、资产情况、工作情况、信用情况和借款信息均会对其未来的违约状况产生影响。本文构建了信用风险评估指标体系（表1）。从表1 可见，评估指标的数据分为数值型数据和非数值型数据，数值型数据的赋值为实际值，而连续的字符（如婚姻状况）通常分为“波段”，然后将每个“波段”替换为二进制虚拟变量。

表1 信用风险评估指标体系及其处理方式

在评估个人借款者违约风险时考虑宏观经济变量可提高信用评估模型对违约率的预测准确性［25］，本文将居民消费指数（CPI）、经济景气指数（ECI）、失业率（URI）、国房景气指数（CERCI）等纳入信用风险评估指标体系。CPI 反映了通货膨胀程度和宏观经济对职工实际工资产生的影响，居民的实际收入影响其还款的压力；ECI 能够直接地表示宏观经济的景气程度；URI 反映了失业率，URI 高，意味着经济情况不景气、失业人数多，借款者中会有一部分面临失业的压力而影响还款情况；CERCI 综合反映了全国房地产业运行的景气状况，该指标的上涨可能是某些房产拥有者财富增加而降低违约风险，或者增加另外一些准备买房或背负房贷的借款者的还款压力而增加违约风险，因此该指标对个人借款者信用风险的影响是不确定的。

3.2 数据来源及处理

基于个人信用卡还款数据的不可得性，因此本文选取P2P平台上的个人借款数据，通过Python 爬虫获取来自于我国P2P网络借贷平台中处于领军企业的“人人贷”的数据。数据集中了1，048，575 个样本，其中未违约人数1，035，133 人、违约人数13，442人。基于数据可非自然分布的研究结论［26］，本文将对样本数据进行了1 ∶1 的平衡处理。在违约案例13，442组的基础上，随机筛选13，442组非违约样本对数据进行平衡处理。数据的描述性统计具体见表2。

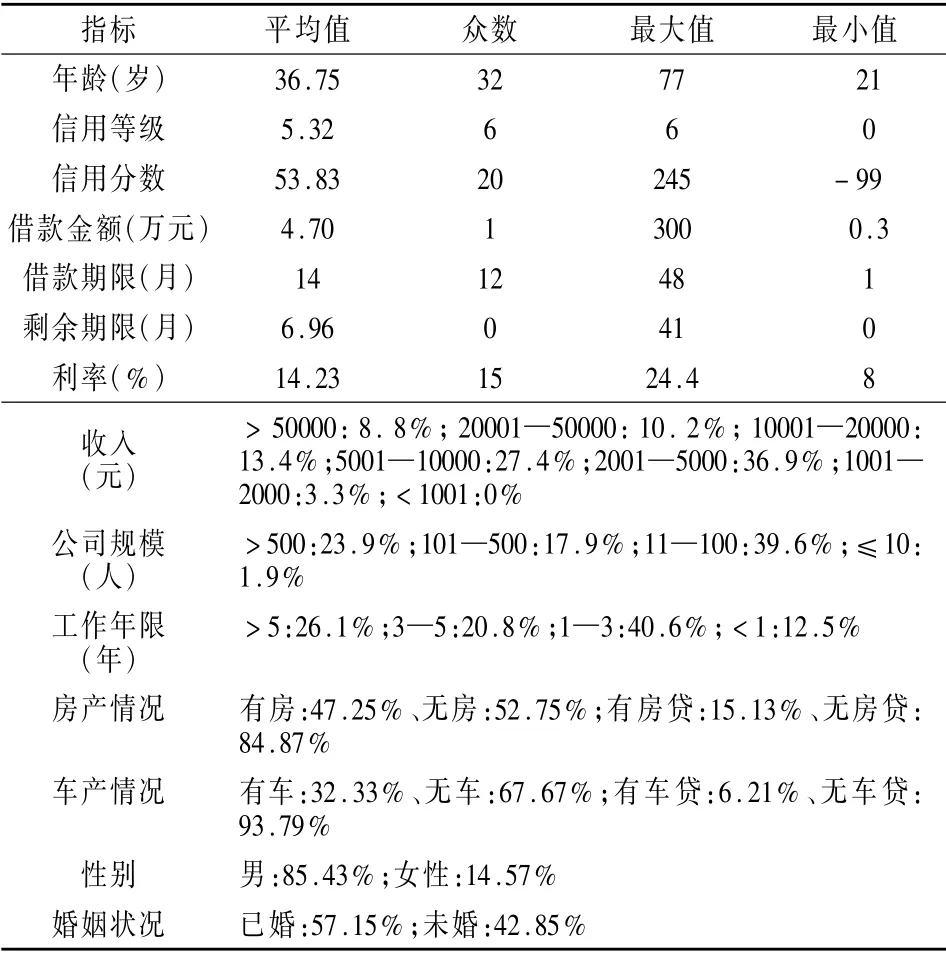
表2 样本的描述性统计

4 实证研究

本文采用十折交叉验证，在违约案例13，442 样本的基础上，随机筛选了13，442 个非违约样本进行研究。其中十分之一的数据，即随机选择1344 个违约样本和1344 个非违约样本组成测试集，其他的12，098 个违约和12，098 个未违约样本随机均匀分布在9 个训练集中，利用训练集的数据进行Lasso变量选择和模型的参数估计。

4.1 Lasso评估指标选择

本文首先对16 个静态指标进行了相关性检验，具体结果见表3。从表3 可见，一些指标间存在着近0.7698 的高度线性相关性。若不进行降维处理，不仅会降低模型的运行效率，也会使实证结果出现过拟合现象，影响模型的精确度，因此本文对指标进行筛选。

Lasso模型是通过构造惩罚函数来达到精简模型的效果，会将一些呈现共线性或者与因变量没有相关性的冗余变量通过将其回归系数设置为0 的方式剔除，保留自变量子集简练且收缩的优点。基于此，本文首先通过Lasso筛选出对违约状况影响显著的协变量指标，再应用Cox 回归模型对借款者的违约风险进行拟合，建立违约预测模型，然后利用训练集的数据拟合出Alpha和Lasso 回归系数的关系（图1）。从图1 可见，在Alpha 取值在10-5和10-3之间时，模型自变量的系数趋于稳定。而模型需要确定具体的调和参数，即最小的λ值来使得模型的筛选误差最小，因此还是需要借助十折交叉检验方法，即公式（12）来确定最小的λ值。基于最小的调和参数值，模型最终筛选了7 个信用风险评估指标，分别是：信用分数、信用等级、年龄、利率、借款期限、剩余期限和收入。

表3 各信用风险评估指标的相关关系

图1 Alpha和Lasso回归系数的关系

4.2 Cox PH模型的参数估计及其检验

根据Lasso模型筛选的7 个变量，在不考虑宏观经济变量的情况下，利用公式（6）得到的参数估计值（表4）。

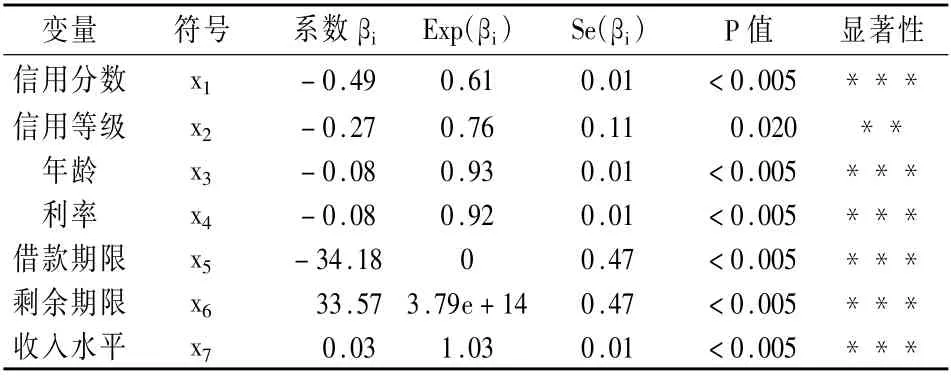
表4 Lasso- Cox PH模型的参数估计

从表4 可见，7 个变量均通过了显著水平为5%的显著性检验（其中6 个变量通过了1%的显著性检验）。信用分数、信用等级、年龄、利率、借款期限对违约的影响是负相关的，剩余期限与违约呈正相关，与预期一致。收入水平与违约状态呈正相关，是由于样本群的收入大部分集中于中低收入，因此违约概率被稀释，导致高收入违约概率反而升高。

在考虑利用生存分析模型时，应首先确定该模型是否适合信用风险评估的问题。这是由于模型的应用存在某些假设前提或者某些特性，这些情况都有可能使得模型与相关数据之间不匹配，因此应首先检验模型对数据的适应性。许多方法都可以达到检验模型对数据适应性的目的，本文通过似然比检验，检验结果见表5。

表5 Lasso- Cox模型的Omnibus检验

表5 中，原假设为H0：βi＝0，备择假设为H1：存在βi≠0。结果显示，模型整体的Sig. ＝0.000 ＜0.05，应拒绝原假设，接受备择假设，即对模型总体检验有显著意义。也就是说，存在至少一个偏回归系数不为零的因素，因此可利用该模型对数据做进一步分析。

4.3 Cox 模型的参数估计

前人的研究表明，宏观经济情况可在一定程度上影响借款者的违约概率。而扩展的Cox 模型（Extended Cox model）是有时间依赖的模型，能很好地结合宏观动态变量进行研究。加入宏观变量后的评估指标共有11 个变量（表6），均通过显著水平为1%的显著性检验。信用分数、信用等级、利率、借款期限、剩余月数、收入、经济景气指数、国房景气指数对违约的影响呈负相关，年龄、失业率、居民消费指数与违约呈正相关。其中，信用分数、信用等级、利率、借款期限、收入、国房景气指数、失业率与违约率的关系是符合预期的，剩余月数与违约率在此时与违约率呈正相关，则可能与宏观经济因素有关，如宏观政策的利好消息，会使得居民的实际收入上涨，进而降低违约率。居民消费指数与违约率的关系主要与通货膨胀有关，在本文中与违约率呈现正相关则说明通货膨胀使货币的购买力降低，增加借款人的还款压力进而增加违约可能性。

表6 加入宏观变量后Lasso- Cox 模型的回归系数及其显著性

Cox 模型与相关数据之间的匹配程度结果见表7。从表7 可见，模型整体的显著性为0.000，小于1%，因此拒绝原假设，接受备择假设，即对模型总体检验有显著意义。也就是说，存在至少一个偏回归系数不为零的因素，可以使用该模型对相关数据进行进一步分析。

表7 加入宏观因素后Lasso- Cox模型系数的Omnibus检验

4.4 预测结果分析

在预测分析中，模型有可能将优质借款人误判为劣质借款人，或者将劣质借款人误判成优质借款者，这都会影响到优质借款者的权益或者侵害投资者的相关权益，因此第一类错误率和第二类错误率与模型的预测效果息息相关。其中，第一类型错误是优质借款人被模型误判为劣质借款人，第二类型错误表示有违约风险的劣质借款人被识别为没有违约风险的优质借款人。在不考虑宏观因素影响的情况下，Logistic、Cox PH 和Lasso- Cox PH 模型各个模型的预测结果见表8。从表8 可见，与Logistic 回归模型相比，Cox PH 模型的预测精确度总体上高达91.11%，远远高于Logistic 模型；而Cox PH 模型和Lasso- Cox PH 模型相比，通过Lasso 对冗余变量进行筛选，Lasso- Cox 模型精度大于将全部指标都纳入模型的Cox模型，且经过Lasso处理后模型的第一类错误率和第二类错误率均大大下降。Lasso - Cox模型犯第一类错误的概率仅有1.41%，犯第二类错误的概率也由Cox PH模型的9.6%下降至7.07%，说明利用Lasso方法进行变量处理是必要的。

表8 Logistic回归、Cox PH和Lasso- Cox PH模型在不含宏观变量时的预测结果

Logistic 回归、扩展的Cox 和Lasso - Cox 模型在含宏观变量时的预测结果见表9。因为Logistic模型为静态回归模型，为了同步考虑宏观变量对其评估结果的影响，根据每一笔借款数据的起始借款日期的宏观月度数据纳入模型，以一个静态的样本来进行实证建模的。而Cox 模型、Lasso - Cox 模型则是借助整个借款期间的宏观月度数据来进行动态建模。从表9 可见，无论是经典的Logistic 模型，还是Cox模型、Lasso - Cox 模型，加入宏观变量后其预测准确度都有一定程度的提升。Logistic模型和Cox模型相比，总体来说Cox模型呈现更高的准确度，因此Cox模型在判断个人借款者是否违约具有更好的表现。而Cox 模型与Lasso - Cox 相比，可以看出经过Lasso变量选择后的Lasso - Cox 模型的预测效果具有更好的提升。在Lasso处理变量后，模型的第一类错误率和第二类错误率均下降了，尤其是Lasso -Cox的第二类错误率接近于0，模型的优度得到进一步提升。

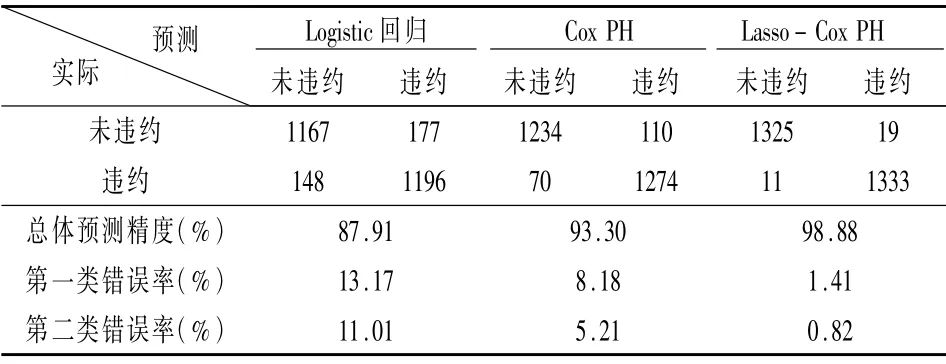
表9 Logistic回归、Cox PH和Lasso- Cox PH在含宏观变量时的预测结果

5 结论与讨论

本文利用“人人贷”平台借款者的借款数据和个人信息建立信用风险评估指标体系，并采用不同的模型进行模拟实验，对Lasso- Cox 模型和Cox 模型、Cox模型和Logistic模型对“人人贷”借款者的违约概率进行了评估，预测结果表明Cox 模型的预测准确率高于Logistic模型的预测准确率。将Lasso 模型和Cox模型结合构造的Lasso- Cox 模型，通过Lasso 模型首先将评估指标进行筛选，再利用Cox 模型进行评估，得到95.76%的预测准确率，预测精度大幅度提升。将动态的宏观变量也纳入到评估指标中，结果发现在加入4 个宏观变量后，各模型的预测效果均有了很好的提升，其中Lasso- Cox 模型的预测准确度高达98.88%。

主要结论：①动态的Cox 模型在信用风险评估中预测精度更高。在评估指标一致时，Logistic 模型的第一类错误率和第二类错误率均高于Cox 模型，而Cox模型能将不同时间点的违约状况考虑进模型，根据不同时间点的基准生存函数得到不同时间点的生存率，因此预测精度更高。②Lasso 方法能很好地识别信用风险评估指标中的重要变量。对于P2P个人借款者来说，他们的信息是高维度的，正因为存在着数十个相关指标，因此有些变量的相关性就很高，出现过拟合现象而降低了模型的精确性。因此，经过Lasso模型对变量进行筛选后的Cox 模型预测精度远远高于不进行指标处理的Cox 模型。③宏观变量是个人借款者信用风险的影响因素，有助于提升信用风险评估模型的预测精度。加入宏观变量的模型预测结果都得到了提升，在考虑宏观变量的条件下，Lasso - Cox 模型预测准确率高达98.88%，这无疑是一个更加有效的评估结果，也在一定程度上说明宏观变量能够增加信用风险评估的准确性，并进一步说明该类变量在个人信用风险评估中的影响因素。

本文对个人信用风险评估方面的贡献表现在两个方面：一是在建立我国个人借款者的信用风险评估指标时引入了动态的宏观经济指标；二是借鉴Lasso模型和Cox 模型的优点，创建了新的Lasso -Cox模型。研究结果表明，Lasso- Cox 模型大幅提高了个人借款者信用风险评估的精度。不足之处在于，由于银行信用卡信息的保密性，本文只能选择P2P平台的数据来进行个人借款者违约风险的预测，数据来源受限。