临界中性Gauss-Bonnet-anti-de Sitter黑洞复杂度演化*
梁华志 张靖仪
(广州大学物理与材料科学学院,广州 510006)
利用Fan 和Liang (Fan Z Y,Liang H Z 2019 Phys.Rev.D 100 086016)研究一般高阶导数引力复杂度的方法,对临界中性Gauss-Bonnet-anti-de Sitter (Gauss-Bonnet-anti-de Sitter,AdS)黑洞的复杂度演化进行研究,并且将研究结果和一般中性Gauss-Bonnet-AdS 黑洞的结果进行了比较.研究发现,二者的复杂度演化的整体规律是一致的,它们的主要区别在无量纲的临界时间上.对于五维的临界中性Gauss-Bonnet-AdS 黑洞,当黑洞视界面为平面或者球面时,不同大小的黑洞的无量纲的临界时间相同,都取到了最小值.当维度超过五维时,不同大小的球对称临界中性Gauss-Bonnet-AdS 黑洞的无量纲临界时间的差异明显要比一般的情况小.这些差异很可能和中性Gauss-Bonnet-AdS 黑洞的临界性有关.
1 引 言
复杂度是量子信息理论中的概念,大致说来,可以将复杂度理解为衡量从一个给定的参考状态构造出一个目标状态的难度的量.给定参考状态|A〉 以及目标状态 | B〉 ,可以定义一个测量这两个量子态之间的距离的特殊“度规”,称为相对复杂度,用 C 表示.相对复杂度的物理含义是从一个参考状态 | A〉 到 一个目标状态 | B〉 所需“门”的最小数目.在量子信息理论中,“门”指的就是简单操作.两个量子态之间通过幺正算符U 相联系,即: | B〉=U|A〉 ,其中,幺正算符U 包含了一系列的“门”.U 有时候也被称为“电路”,尽管它没有任何的周期性.
由于受到黑洞的贝肯斯坦-霍金熵正比于黑洞视界面积的启发,’t Hooft[1]在1993 年首次提出了全息原理,随后Susskind[2]对全息原理进行了进一步的研究和阐述.1997 年,Maldacena[3]在IIB 型超弦理论背景下,利用N 张重合的D3-brane 的低能极限,找到了全息原理的第一个,也是极其重要的一个具体实现的例子—AdS/CFT (anti-de Sitter/conformal field theory)对偶.AdS/CFT 对偶指出(d + 1)维的反德西特时空中的引力理论等价于d 维边界的共形场论.之后,Witten[4]和Gubser 等[5]分别独立给出了一套数学上的对应关系.一直以来,除了几个简单的模型以外,想要直接去计算黑洞的复杂度是十分困难的.AdS/CFT对偶为黑洞复杂度的研究打开了一扇新的窗户.基于AdS/CFT 对偶,Susskind 研究组先后提出了复杂度/长度对偶[6]以及复杂度/体积对偶[7,8],经过逐步改进,最后发展出了复杂度/作用量对偶[9,10].复杂度/作用量对偶指出d 维边界全息状态的量子计算复杂度对偶于(d + 1)维Wheeler-Dewitt 片的经典作用量.复杂度/作用量对偶把黑洞复杂度问题归结为对引力作用量的计算.经过几年发展,人们已经利用复杂度/作用量对偶得到了许多黑洞复杂度演化的结果[10−35].
给定一个宇宙学常数,一般的Gauss-Bonnet引力都会存在两个AdS 时空作为它的真空解.研究发现,存在一个参数空间的临界点,两个AdS 真空合并成一个,这种临界的引力理论没有传播子,因此一般的引力子模型不再适用,这种引力理论被形象地称为没有引力子的引力[36].临界中性Gauss-Bonnet-anti-de Sitter (Gauss-Bonnet-anti-de Sitter,AdS)黑洞性质上和一般的情况有很大不同,进一步研究临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化,不仅对黑洞复杂度研究的发展有所贡献,同时对Gauss-Bonnet 引力临界性的研究也有一定意义.
2019 年,Fan 和Liang[11]得到了一般高阶导数引力的复杂度演化公式,并利用数值方法对平面(k=0 )的Gauss-Bonnet-AdS 黑洞以及平面(k=0 )的三阶Lovelock-AdS 黑洞的复杂度演化进行了详细的讨论.后来,本研究组利用Fan 和Liang 给出的一般高阶导数引力的复杂度演化公式,把他们对中性Gauss-Bonnet-AdS 黑洞复杂度的演化推广到了一般的情况(k任意),得到了一般中性Gauss-Bonnet-AdS 黑洞的复杂度演化公式,并利用数值方法画出了演化图和微分图,找出了不同视界几何的中性Gauss-Bonnet-AdS 黑洞复杂度演化的共同点以及差异[12].本文将进一步利用Fan 和Liang 给出的一般高阶导数引力的复杂度演化公式,研究临界中性Gauss-Bonnet-AdS 黑洞复杂度演化,通过和一般中性Gauss-Bonnet-AdS黑洞的结果作对比[12],找出其临界性对复杂度演化的影响.
2 临界中性Gauss-Bonnet-AdS 黑洞复杂度演化
2.1 临界点
对于含有宇宙学常数的一般的Gauss-Bonnet引力,都会允许两个AdS 时空作为它的真空解,这种一般的Gauss-Bonnet 引力理论可以用线性引力子模型去解释,线性引力子在其中一个AdS 真空中具有正的动能,而在另一个AdS 真空中具有负的动能.研究发现,Gauss-Bonnet-AdS 引力理论的参数空间存在一个的临界点,两个AdS 真空会合并成一个,同时动能项的有效耦合常数消失,这种临界点的引力理论没有传播子,因此一般的引力子模型不再适用,这种引力理论被形象地称为没有引力子的引力[36].参数空间的临界点也可看作是一个相变点,超过这个临界点,引力理论不再具有最大对称性的时空解.1983 年,Hawking 和Page发现AdS 黑洞的热力学系统存在Hawking-Page相变[37].后来研究发现,随着黑洞温度的升高,5 维的中性球对称(k=1 )的Gauss-Bonnet-AdS黑洞同样存在相变现象[38],类比于范德瓦耳斯系统,黑洞系统在相变点的临界指数 (α,β,γ,δ) 分别为α=0,β=1/2,γ=1,δ=3 .需要特别强调的是,本文所说的Gauss-Bonnet-AdS 引力的临界点和Hawking-Page 相变的临界点并无关系.
下面先给出中性Gauss-Bonnet-AdS 黑洞参数空间临界点的临界条件.Gauss-Bonnet-AdS 引力包含两个非平凡的参数空间,分别是裸宇宙学常数Λ0以及耦合常数λ.首先,可以利用裸宇宙学常数Λ0去定义一个有效宇宙学常数Λ[36]:

其中,
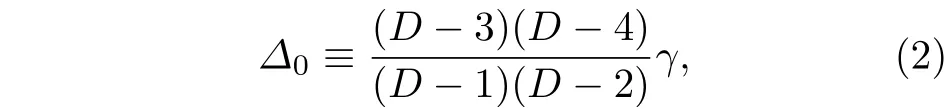
这里的γ表示Guass-Bonnet-AdS 引力的拉格朗日密度L中的系数,分别有

此处的λ为Gauss-Bonnet 耦合常数,它是表征Gauss-Bonnet 引力和爱因斯坦引力差异的参数.当λ=0 时,Gauss-Bonnet 引力会退回到爱因斯坦引力.Gauss-Bonnet 引力的耦合常数的取值被边界理论的微观因果关系所强烈约束.关于Gauss-Bonnet 耦合常数的取值,Brigante 等基于AdS/CFT 对偶,最先给出了5 维Gauss-Bonne黑洞耦合常数的上界为“λ≤9/100 ”[39,40].而后,Buchel 和Myers 进一步给出了5 维Gauss-Bonnet黑洞耦合常数的下界为“λ≤−7/36 ”[41].最 后,Camanho 和Edelstein 指 出,一 个D维Gauss-Bonnet 引力的耦合常数的取值范围为[42]
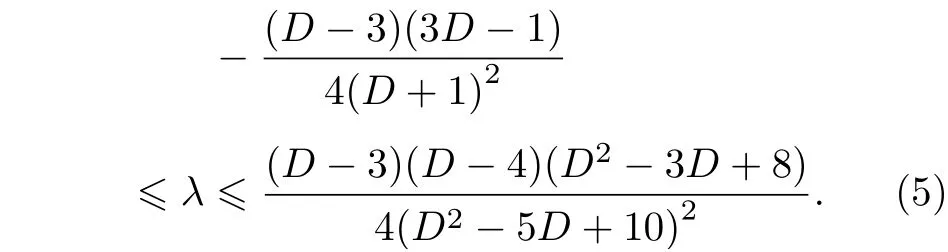
由(5)式可以看出,当D=5 时,(5)式给出的Gauss-Bonnet 耦合常数的上界以及下界跟前人得到的结果[39−41]完全一致.对于一个负的λ,线元的解将会在视界内有限半径处存在另外一个奇点.为了避免这种情况以及考虑到“当λ=0 时,Gauss-Bonnet 引力会退回到爱因斯坦引力”,所以对Gauss-Bonnet 耦合常数的取值作了进一步的限制,即要求λ>0 .从弦论的角度看,这也是一个物理上感兴趣的例子.因此,本文中的Gauss-Bonnet耦合常数所允许的范围为

通过对(1)式进行求解,可以求得两个有效宇宙学常数Λ±分别为
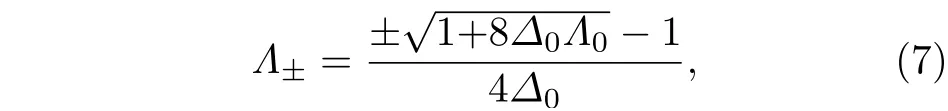
这里的两个有效宇宙学常数Λ±分别对应着两个AdS 时空.
对于(7)式,一般中性Gauss-Bonnet-AdS 黑洞要求Λ±是一个实数,因此有

当(8)式取等号时,就得到了中性Gauss-Bonnet-AdS 黑洞的临界条件,即

或

在临界条件(9)式或(10)式下,两个有效宇宙学常数Λ±相等,即两个AdS 时空合并成了一个,此时有

综合(2)式、(4)式和(10)式,可推导出中性Gauss-Bonnet-AdS 黑洞关于参数空间的临界条件为

2.2 临界中性Gauss-Bonnet-AdS 黑洞的线元表达式
对于一个时空维度为D(D≥5)的一般中性Gauss-Bonnet-AdS 黑洞,它的线元表达式为

这里度规函数f(r)为
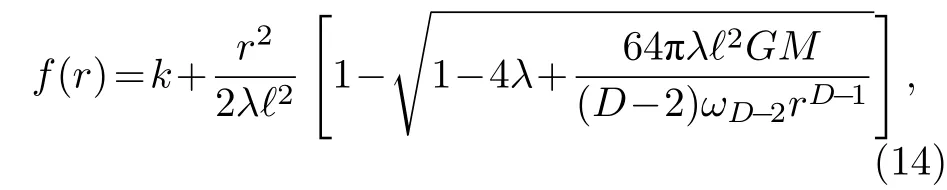
其中,k=1,0,−1 分别表示视界面为球面、平面以及双曲抛物面的黑洞;ℓ为AdS 半径;M为黑洞质量;ωD−2是与视界面几何相关的余二维的单位体积.Gauss-Bonnet 耦合常数λ定义如度规函数(14)式所示.由(14)式可以看出,对于一个负的λ,(13)式的解将会在视界内有限半径处存在另外一个奇点.可以利用参数g把有效宇宙学常数Λ重新定义为

根据前面的分析,在临界条件下

综合(15)式和(16)式,有

将临界条件(12)式以及(17)式代入(14)式中,可以得到

其中,

(18)式就是临界中性Gauss-Bonnet-AdS 黑洞的度规函数,进一步地,可以利用(19)式,解得黑洞质量M为

不难证明,(20)式给出的黑洞质量表达式和利用Wald formalism 得到的结果是一致的[43−45].根据Gauss-Bonnet-AdS 引力的Wald 公式,有

这里的f是度规函数f(r) 的简写.对于临界中性Gauss-Bonnet-AdS 黑洞,度规函数如(18)式所示,故

将(22)式代入(21)式,化简后可以得到

对于渐进无穷远,即r→∞,有δH∞=δM.根据(23)式可以得到

不难看出,由(24)式得到的黑洞质量表达式和(20)式给出的结果完全一致.
进一步,根据f(rh)=0 ,可以得到
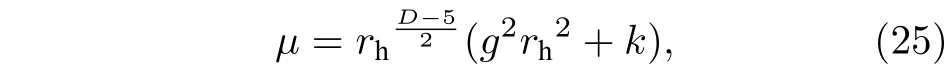
这里rh为黑洞事件视界半径,需要指出的是,(25)式是一个重要的化简条件.
2.3 临界中性Gauss-Bonnet-AdS 黑洞热力学量
根据之前的研究[11,12],黑洞复杂度的演化结果依赖于黑洞的热力学量,为了进一步研究临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化,需要先计算出相关的热力学量.Gauss-Bonnet-AdS 黑洞的温度函数以及Wald 熵函数定义在任意的超曲面t=const 以及r=const 上,定义式分别为[11]
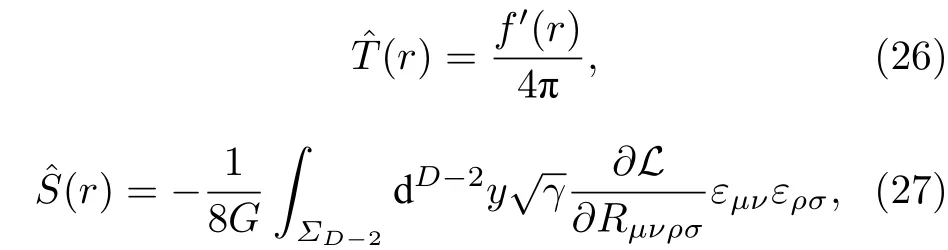
其中εµν表示超曲面的副法矢.将(3)式的拉格朗日密度以及(18)式的度规函数分别代入上述定义式,不难推导出临界中性Gauss-Bonnet-AdS 黑洞的温度函数以及Wald 熵函数分别为

在(28)式和(29)式的化简中,利用了(25)式的条件,需要注意的是(28)式和(29)式并不是黑洞真正的温度和熵,后者是定义在黑洞事件视界上的.可以证明,当超曲面在晚期接近黑洞事件视界时,它们的确会变成黑洞真正的温度和熵.因此临界中性Gauss-Bonnet-AdS 黑洞的温度T以及熵S分别为

2.4 临界中性Gauss-Bonnet-AdS 黑洞复杂度演化公式
根据复杂度/作用量对偶 (complexity/action duality,CA 对偶)[10],有

其中,C表示复杂度,I表示作用量,π是一个比例系数,没有特指数学上的圆周率.ℏ 是普朗克常数,这里使用自然单位制,ℏ =1 .相比于黑洞的复杂度,更多的时候关心的是黑洞复杂度的增长速率dC/dt,把(32)式对时间t求导,可以得到

这里的 dI/dt表示作用量增长速率.根据Fan和Liang[11]给出的结果,对于一个高阶导数引力理论下的中性黑洞,它的复杂度在临界时间tc以前(t≤tc)不演化,即

而在临界时间tc以后(t>tc),它的复杂度增长速率为
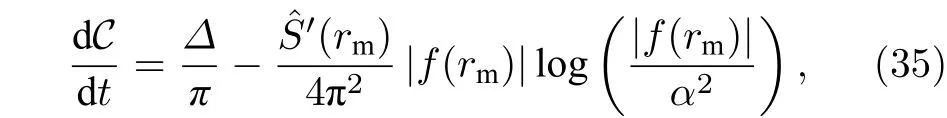
这里的∆表示总作用量增长速率的晚期极限.图1给出了一般的中性双边AdS 黑洞Wheeler-Dewitt片的示意图,rm为Wheeler-Dewitt 片两条过去类光边界交界处的径向坐标.需要特别说明的是,上文所说的临界时间tc指的是Wheeler-Dewitt片两条过去类光边界相交的“节点”恰好落在过去奇点上所对应的时间t,与前文所说的临界Gauss-Bonnet-AdS 黑洞的临界点并无关系.这里的时间t指的是两侧边界时间之和,即

其中乌龟坐标r∗(r)定义为[11]
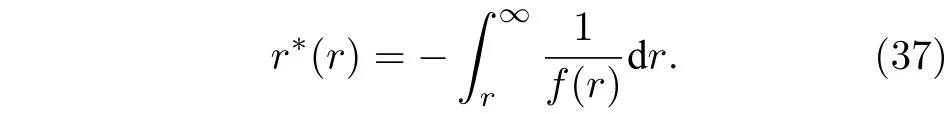
所以r∗(∞)=0.

图1 一般的中性双边AdS 黑洞Wheeler-Dewitt 片Fig.1.The Wheeler-DeWitt patch for a general neutral two-sided AdS black hole.
引力作用量的Gibbons-Hawking-York(GHY)表面项的定义式以及它的增长速率公式为[11]
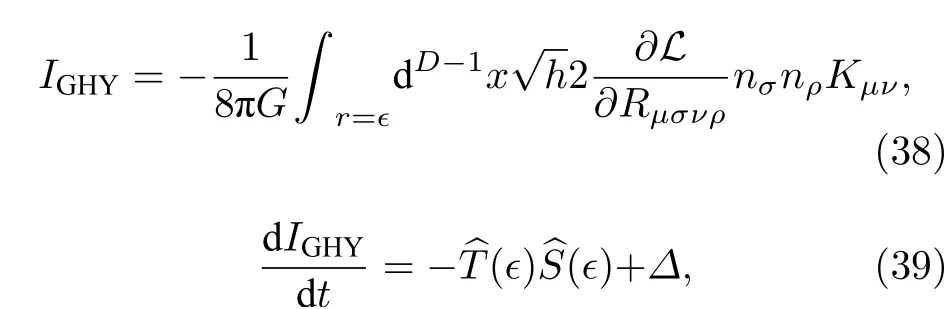
其中Kµν为外曲率.根据(38)式、(39)式及(18)式,可以推导出临界中性Gauss-Bonnet-AdS 黑洞的总作用量增长速率晚期极限∆为
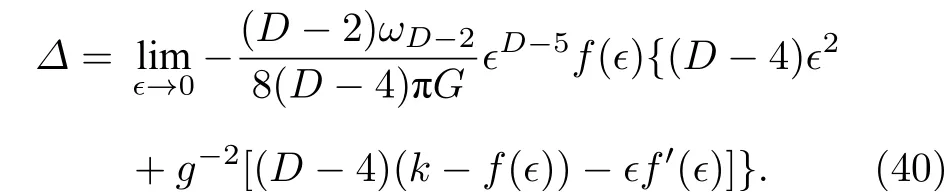
进一步计算,可以得到
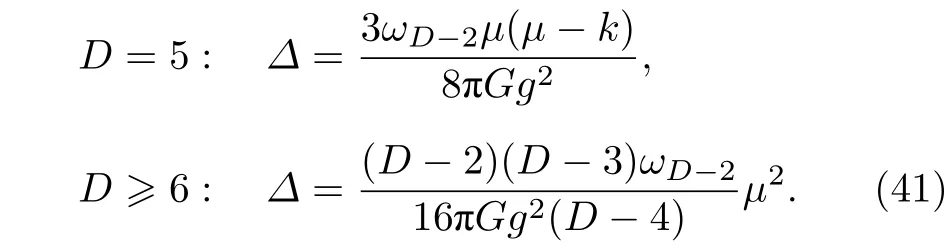
至此,只要把(18)式的度规函数、(29)式的Wald熵函数以及(41)式的作用量增长速率的晚期极限代入(35)式,就可得到临界中性Gauss-Bonnet-AdS 黑洞复杂度演化的公式.
2.5 数值结果
为了更直观地看出临界中性Gauss-Bonnet-AdS 黑洞复杂度演化的情况,需要进行数值分析,利用数值方法画出黑洞复杂度的演化图以及微分图.最直接了当的方法是利用数值方法去求解(36)式,得到rm随时间t的演化函数,然后代入(35)式从而得到复杂度演化的函数,从而进一步去画出复杂度演化的图像,理论上这样求解并不困难.但是需要注意的是,由于乌龟坐标r∗(r) 在事件视界rh处是奇异的,使得直接求解(36)式难以进行.和Fan 和Liang[11]的文章一样,为了解决这个问题,必须引入新的函数F(r) 以及H(r)

其中一个有用的关系式是F(rh)=2πT/rh.
此时,乌龟坐标r∗(r) 可以重新表示为
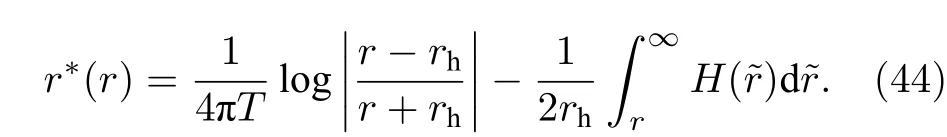
不难看出,乌龟坐标的奇异部分已分离到(44)式右边第一项,现在可以很容易得到乌龟坐标的数值解.
同时,时间t以及临界时间tc也可以分别重新表示为
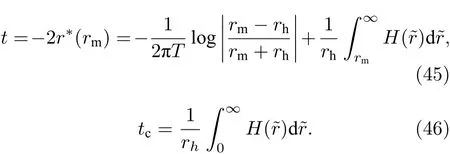
在数值方法中,本研究组习惯采用无量纲的量.因此本文采用无量纲的时间t/β=Tt,其中β表示热时间β=1/T.此时,无量纲的时间Tt以及临界时间Ttc分别表示为

同样地,复杂度增长速率也需要通过除以晚期极限来无量纲化,即

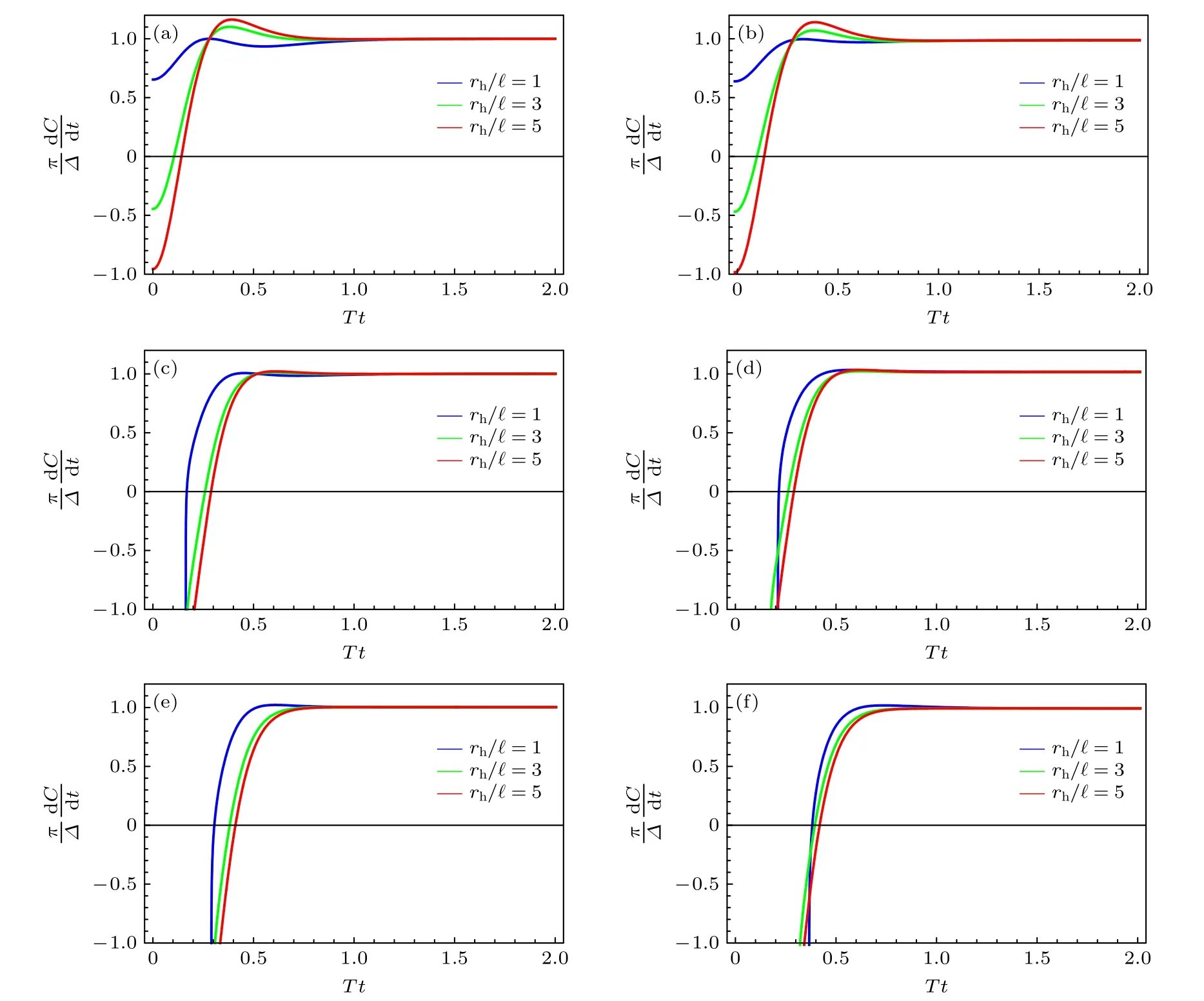
图2 临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化图 (a) D =5,k =0 ; (b) D =5,k =1 ; (c) D =6,k =0 ; (d) D =6,k =1 ; (e) D =7,k =0 ; (f) D =7,k =1Fig.2.Complexity evolution diagram of the critical neutral Gauss-Bonnet-AdS black holes: (a) D =5,k =0 ; (b) D =5,k =1 ;(c) D =6,k =0 ; (d) D =6,k =1 ; (e) D =7,k =0 ; (f) D =7,k =1 .
下面利用数值方法给出临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化的数值结果.图2 为用数值方法画出的不同大小的 D =5,6,7 维的临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化图,横坐标表示无量纲的时间 Tt ,纵坐标表示无量纲的复杂度增长速率,其中,k =0,1 ,rh/ℓ=1,3,5.图3 为对应的复杂度微分图,横坐标表示无量纲的时间 Tt ,纵坐标表示无量纲的复杂度微分,其中,复杂度微分 δ C =C(t)−C(tc) 通过对dC/dt积分得到.为了方便画图,在图2 和图3 中,已经让 G =α=1 ,ωD−2=16π .表1 和表2 分别列出了不同大小以及不同维度的临界中性Gauss-Bonnet-AdS 黑洞的无量纲的临界时间 T tc.
根据数值分析的结果,可以看出临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化和一般中性Gauss-Bonnet-AdS 黑洞的复杂度演化[12]的整体规律是一致的.复杂度增长的整体趋势都是先增长到一个局部的极大值,再开始下降,最后趋近于晚期极限.而且随着维度D 的增加,相同大小的临界中性Gauss-Bonnet-AdS 黑洞的复杂度演化的图像会整体往右移,说明对于相同大小的临界中性Gauss-Bonnet-AdS 黑洞来说,维度越高,相应的无量纲的临界时间 T tc越大.当 k =0 时,不同大小的临界中性Gauss-Bonnet-AdS 黑洞无量纲的临界时间 T tc总是相同的.但是当 k =1 ,D ≥6 时,不同大小的黑洞无量纲的临界时间 T tc却不再相同,在相同维度下,黑洞越大( rh/ℓ 的值越大),无量纲的临界时间 T tc越小,而且维度越高(D 越大),不同大小黑洞的无量纲的临界时间 T tc差别越大.同时也发现,大黑洞( rh/ℓ=3,5 )的复杂度演化图无论是位置还是演化的趋势整体上都非常相似,而小黑洞( rh/ℓ=1 )的复杂度演化图和大黑洞的差别较大.

图3 临界中性Gauss-Bonnet-AdS 黑洞的复杂度微分图 (a) D =5,k =0 ; (b) D =5,k =1 ; (c) D =6,k =0 ; (d) D =6,k =1 ; (e) D =7,k =0 ; (f) D =7,k =1Fig.3.Complexity difference diagram of the critical neutral Gauss-Bonnet-AdS black holes: (a) D =5,k =0 ; (b) D =5,k =1 ; (c) D =6,k =0 ; (d) D =6,k =1 ; (e) D =7,k =0 ; (f) D =7,k =1 .
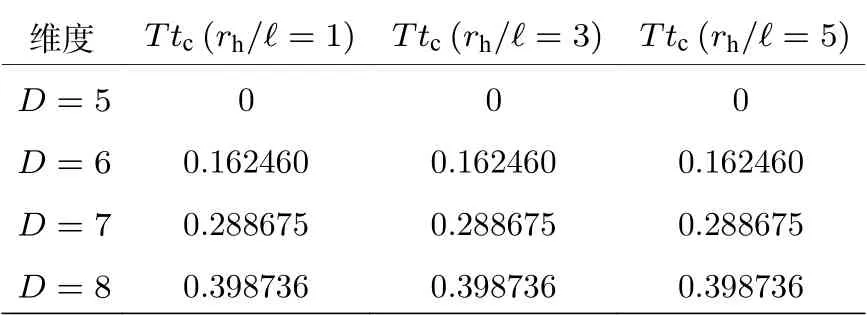
表1 k =0 时,临界中性Gauss-Bonnet-AdS 黑洞无量纲的临界时间 T tc ( λ =0.05 )Table 1.Dimensionless critical time T tc of critical neutral Gauss-Bonnet-AdS black holes ( λ =0.05 )for k =0 .
但是临界中性Gauss-Bonnet-AdS 黑洞复杂度演化也有和一般中性Gauss-Bonnet-AdS 黑洞复杂度演化不同的地方,二者的差别主要体现在无量纲的临界时间Ttc上.对于临界中性Gauss-Bonnet-AdS 黑洞,当D=5 时,不仅是k=0 的不同大小黑洞的无量纲的临界时间Ttc相同,而且k=1 的不同大小黑洞的无量纲的临界时间Ttc也都相同,同时k=0 和k=1 的不同大小黑洞的无量纲的临界时间Ttc都趋近于0,由于要求Ttc≥0 ,所 以k=0,1 ,D=5 的 临 界 中 性Gauss-Bonnet-AdS 黑洞的无量纲临界时间Ttc都取到了最小值.同时也发现,随着维度D的增加,k=1 ,D≥6 的不同大小临界中性Gauss-Bonnet-AdS黑洞之间的无量纲临界时间Ttc的差别明显要小于一般中性Gauss-Bonnet-AdS黑洞的情况.

表2 k =1 时,临界中性Gauss-Bonnet-AdS 黑洞无量纲的临界时间 T tc ( λ =0.05 )Table 2.Dimensionless critical time T tc of critical neutral Gauss-Bonnet-AdS black holes ( λ =0.05 )for k =1 .
3 结论与展望
通过计算,得到了临界中性Gauss-Bonnet-AdS黑洞的复杂度演化公式,并用数值方法画出了它的复杂度演化图以及微分图,最后和一般中性Gauss-Bonnet-AdS黑洞的复杂度演化结果作对比.由于临界Gauss-Bonnet-AdS黑洞本质上还是属于Gauss-Bonnet-AdS黑洞,所以发现二者的复杂度演化的整体规律是一致的.但又由于Gauss-Bonnet-AdS黑洞临界性的影响,二者的复杂度演化又有一些明显的不同.这些不同主要体现在无量纲的临界时间Ttc上.
相同点1)复杂度增长的整体趋势都是先增长到一个局部的极大值,再开始下降,最后趋近于晚期极限;2)随着维度D的增加,复杂度演化的图像会整体往右移,即无量纲临界时间Ttc增大;3)当k=0时,不同大小的黑洞无量纲的临界时间Ttc总是相同的;4)当k=1 ,D≥6时,不同大小的黑洞无量纲的临界时间Ttc不相同,黑洞越大(rh/ℓ的值越大),无量纲的临界时间Ttc越小,而且维度越高(D越大),无量纲的临界时间Ttc差别越大5)大黑洞(rh/ℓ=3,5)的复杂度演化图,无论是位置还是演化的趋势整体上都非常相似,而小黑洞(rh/ℓ=1)的复杂度演化图和大黑洞的差别较大.
不同点1)当k=1 ,D=5时,不同大小的一般中性Gauss-Bonnet-AdS黑洞的无量纲的临界时间Ttc不相同,但是不同大小的临界中性Gauss-Bonnet-AdS黑洞的无量纲的临界时间Ttc都相同,而且和k=0,D=5的无量纲的临界时间Ttc一样,都取到了最小值;2)k=1 ,D≥6的不同大小的临界中性Gauss-Bonnet-AdS黑洞之间的无量纲临界时间Ttc的差别明显要小于一般中性Gauss-Bonnet-AdS黑洞的情况.
分析后知道,当k=0,1,D=5时,不同大小的临界的中性Gauss-Bonnet-AdS黑洞的无量纲临界时间Ttc的积分函数H(r) 会趋近于0,所以无量纲的临界时间Ttc都为0,均取到了最小值,这是数学上的必然结果.猜测这种无量纲的临界时间T tc的差异现象可能和Gauss-Bonnet-AdS黑洞的临界性有关.
研究发现,临界中性Gauss-Bonnet-AdS黑洞复杂度演化和一般的情况确实有一些明显的差别,这对中性Gauss-Bonnet-AdS黑洞临界性的研究是有指导性意义的.但是现阶段对于这种临界的高阶导数引力黑洞的复杂度演化的研究还远远不够,期待后续可以对更多临界的高阶导数引力黑洞的复杂度演化进行研究,特别是三阶的临界Lovelock-AdS黑洞,这样会知道更多高阶导数引力黑洞的临界性的细节.
感谢广州大学天体物理中心范仲英老师的讨论.

