农业科技资源错配对全要素生产率影响——基于门槛效应的实证研究

杨传喜，王修梅，王亚萌

（1.桂林理工大学商学院，广西桂林 541004；2.西北农林科技大学经济管理学院，陕西杨凌 712100）

农业科技资源结构性错配会带来一定程度的配置效率损失［1］，改善农业科技资源错配成为提高农业全要素生产率的途径之一［2］。近年来，资源错配及其对全要素生产率影响的研究得到相关学者的密切关注。国内学者以中国制造业为研究对象，从不同角度出发，并未得到一致的研究结论。涂正革等［3］运用随机前沿生产模型，发现科技资源的配置效率对于全要素生产率的影响并不显著。姚战琪［4］、曾先锋等［5］也证实资源错配对全要素生产率没有作用。也有学者研究发现，当资源不能得到有效配置时全要素生产率会受到影响。朱喜等［6］研究认为消除农业资源错配，农户的农业TFP 有望再增长20%以上。因此，农业科技资源错配是否一定会降低农业全要素生产率？农业科技资源错配程度与全要素生产率两者之间的关系如何？对于这些问题展开研究，有助于更加全面的把握农业科技资源错配对农业全要素生产率的影响机制，从而优化农业科技资源配置提升农业全要素生产率。基于此，本文采用门槛效应模型，分析农业科技资源错配与全要素生产率之间的非线性关系，厘清在不同的农业科技资源错配区间对于农业全要素生产率的影响，寻找改善农业科技资源错配提升农业全要素生产率的方法。与以往文献相比，本文的创新点主要是研究方法运用的创新，已有文献主要是研究他们之间的线性关系，而本文从门槛效应视角来研究农业科技资源错配与全要素生产率的非线性关系。

1 研究方法及数据来源

1.1 面板模型构建

为探究农业科技资源错配与全要素生产率的非线性关系，本文采用Hansen 提出的非线性面板门限回归模型,该方法从数理统计角度识别未知变量的数据特征，从而避免人为划分门槛区间带来的偏差。以农业科技资源总错配指数作为门限变量，构建门限面板回归模型，检验农业科技资源错配与农业全要素生产率之间的非线性关系。根据本文选取的变量，构建门限模型如下：

本文基本方程为：

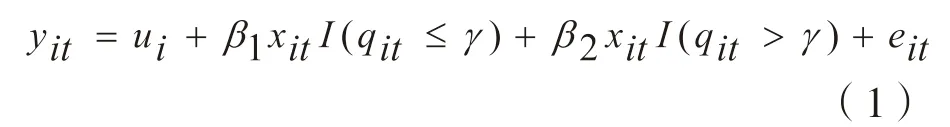
（1）农业科技资源错配与全要素生产率的单重门限模型：

农业科技资源错配与全要素生产率的双重门限模型：

其中,省份和年份用i 和t 表示。农业全要素生产率（TFP）为被解释变量；农业科技资源总错配指数misait同为核心解释变量和门槛变量；Hit为控制变量，包括农业科技人员素质、农业信息化水平、农村经济发展水平。

1.2 变量与数据说明

本文选取1999—2017 年为研究区间，以25 个有效省（市、区）农业科学院为研究对象，利用门槛效应模型对农业科技资源错配与全要素生产率之间的关系进行验证。本文数据来源于《中国农业科技统计资料汇编》《中国统计年鉴》。对于部分缺失数据，进行了有效补充。对农业科技活动经费内部支出涉及货币量的指标以1999 年数据为基期进行平减，在进行门槛回归时，除农业科技资源总错配指数外其他变量都取对数处理。对于农业全要素生产率与农业科技资源错配指数测算的数据指标如表1 所示。在对1999—2017 年各省份农业科技资源错配情况进行分析时，将选取的25 个省划分为六大区域，在各个区域内对各省份的错配情况进行比较分析，从而更能明显的分析我国农业科技资源的错配情况及区域错配特征。六大区域分为：华北区、东北区、华东区、中南区、西南区、西北区。

1.2.1 被解释变量农业全要素生产率

运用DEA－Malmquist 方法测算农业全要素生产率，对专利数量、发表科技论文数以及出版科技著作运用熵值法加总。以此作为评价农业科学院创新产出的指标，以农业科技活动人员与平减后的农业科技活动经费支出作为投入变量，构建农业全要素生产率测算指标体系，见表1。

表1 农业全要素生产率、农业科技资源错配测算指标

1.2.2 门限变量

（1）农业科技人力、财力资源错配指数。为了准确的计算农业科技人力、财力错配指数，需要估计两者的产出弹性。本文在Hesih 等［7］关于资源错配研究的基础上假定选定的25 个省份在农业科技生产过程中都投入了农业科技人力、财力资源L、K 两种要素。同时，用来表示资源要素价格扭曲，则选定的25 个省份在实际生产过程中投入的农业科技人力资源、农业科技财力资源的价格分别为

假设生产函数为规模报酬不变的C-D生产函数，即：

地枫皮作为狭域分布的珍稀植物，多分布于裸露的石灰岩山顶，长期生长在干旱、水分不足、光照强烈、土层浅、伴生物种少等极端干旱的环境中。而叶片的形态特征是对环境适应性最直观的反映[18]。研究表明，叶脉发达、叶片的角质厚、栅栏组织发达、气孔密度大等特征，都有利于适应干旱环境。叶脉结构直接影响叶片对外界环境因子(如温度、水分有效性)胁迫的敏感性[19]。研究发现,地枫皮中脉发达，平均厚度约546.67 μm，木质部所占比例约为50%,具有丰富的木纤维和韧皮纤维，这种类似茎的结构大大加强了中脉的支持力和输导能力，3个不同分布区的地枫皮中脉厚度随着海拔高度的增加而增大，说明地枫皮具有较强的耐旱能力。

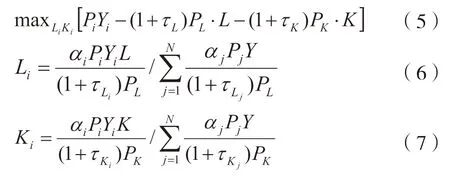
根据上文推导出来的价格扭曲的均衡解，可以进一步得出农业科技资源绝对扭曲系数：

农业科技资源配置的绝对扭曲系数反映的是农业科技资源投入无扭曲价格的加成程度，而农业科技资源的相对扭曲程度才是农业科技资源在各省份之间错配的主要原因。因此，将i 区域的农业科技产出所占总省份的总农业科技产出的比例表示为，农业科技资源要素贡献值为则农业科技资源的相对扭曲系数可以表示为：

联立（3）式和（5）式可得i 区域的农业科技资源相对扭曲系数为：

（2）农业科技资源总错配指数(TMis)的计算。借鉴白俊红等［8］的方法，根据本文计算得出农业科技财力资源错配指数和农业科技人力资源错配指数，通过取平均数的方式获得历年各地区农业科技资源总错配指数。

1.2.3 控制变量

对于控制变量的选取主要有以下三个：（1）地区经济发展水平采用人均GDP(AGDP)表示。（2）农业科技活动人员素质(RL)，采用各省科技活动人员受教育年限来表示，具体计算方法是借鉴陈钊等［9］的加权求和方法，将各阶段受教育年限作为不同教育阶段的权重。（3）农业信息化水平(IN)参照韩海彬等［10］做法，具体选用村居民家庭每百户黑白电视机、彩色电视机、电话机拥有量（部）作为农业信息化指标。

2 实证结果与分析

2.1 农业科技资源错配程度分析

如表2 所示，我国25 个省份农业科技资源都存在着不同程度的农业科技人力、财力资源错配情况，同一省份在不同年份之间有较大波动，且农业科技人力资源在北京、河北、吉林、辽宁、浙江、江西这几个省份错配情况较为严重，其他省份也表现为不同程度的农业科技人力资源错配情况但错配指数在1 附近波动，在这25 个省份之中大多还是农业科技人力资源配置不足。

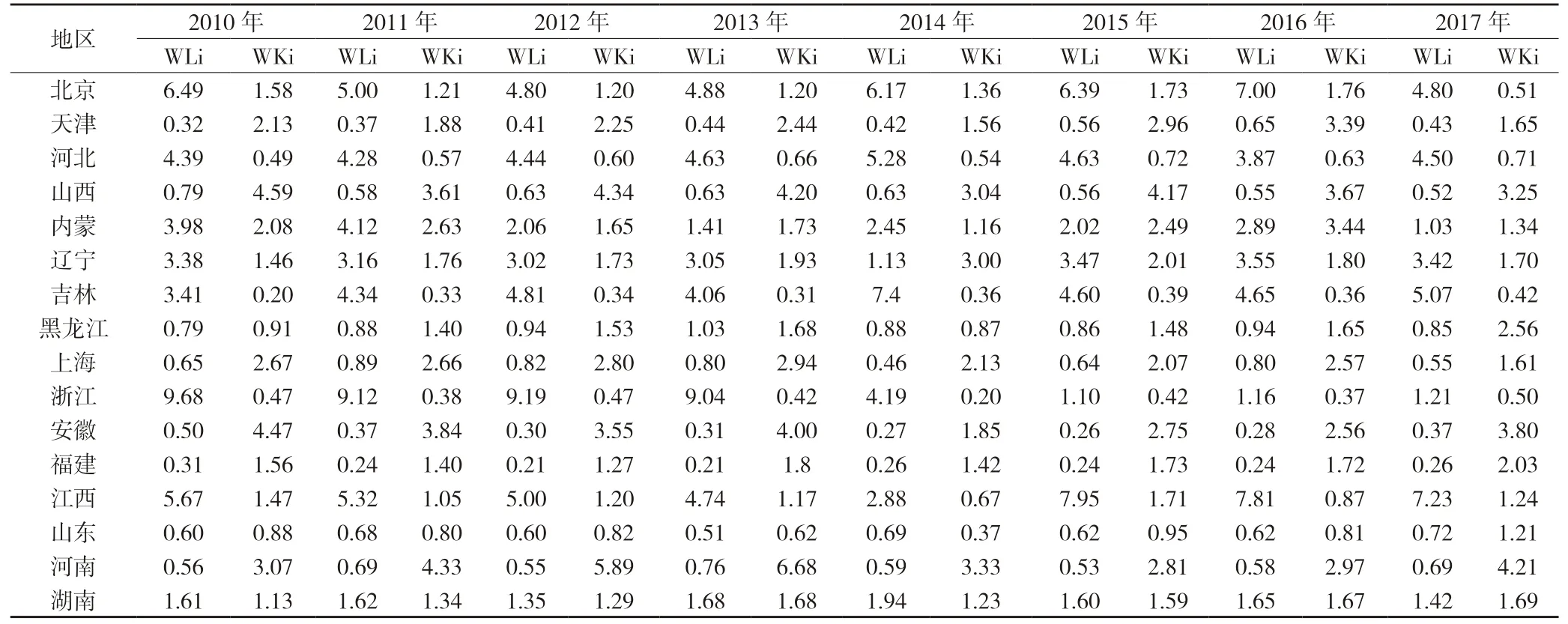
表2 2010—2017 年农业科技资源错配情况

表2 （续）

从划分的六大地区华北地区、东北地区、华东地区、中南地区、西南地区、西北地区来看：（1）华北地区不同省份在不同年份存在不同的错配情况，北京、内蒙农业科技人力、财力错配系数都大于1，表明北京、内蒙这两个省份农业科技人力、财力资源都存在严重过剩。山西、天津农业科技财力错配系数大于1；农业科技财力资源存在过剩，山西实际财力投入是有效投入3～4 倍，天津实际财力投入是有效投入的2 倍以上，山西省是华北地区农业科技财力资源错配情况最为严重的省份。（2）东北地区辽宁省农业科技人力、财力资源都存在配置过剩，吉林省则表现为严重的农业科技人力资源配置过剩；黑龙江农业科技财力资源配置过剩。东北地区近年来产能过剩问题最为严重，农业科技财力资源大量闲置。辽宁、黑龙江农业科技财力资源配置过剩整体呈波动趋势。（3）华东地区安徽作为我国中部的崛起省份，投入了大量的财力资源，但安徽农业科技占的比重并不大，大量的投入使得安徽农业科技财力资源配置过剩现象十分严重，2010 年财力实际投入是有效投入的4 倍以上，但从2014 开始，安徽省农业科技财力资源错配情况在不断的得到改善，财力资源相对错配系数已降到2017 年的3.8。上海、福建、江西三省的农业科技财力资源错配无明显变化趋势，总体趋势W上海＞W福建＞W江西。而浙江省农业科技财力资源配置不足，农业科技人力资源表现严重的过剩情况。(4)中南地区河南、湖南、广西、海南都表现为农业科技财力资源配置过剩，农业科技人力资源配置不足情况主要因为中南部地区科技活动人员较少无法合理的运用科技活动经费使其转化为科技成果。(5)西南地区重庆、西藏都表现为农业科技人力、财力资源配置过剩，云南农业科技财力资源配置存在过剩，农业科技人力资源配置不足。（6）西北地区甘肃、青海、新疆农业科技财力资源都表现为资源配置过剩现象但并不明显，农业科技人力资源配置不足主要因为西部地区对于科技活动人员的供给小于其需求，造成西部地区由于人才的缺乏不能很好的进行科技成果的转化。

2.2 门槛面板回归分析

本文采用ADF 法进行单位根检验，结果见表3。农业科技资源总错配指数、农业科技活动人员素质在0 阶和1 阶情况下均保持平稳，而农业信息化水平和农村经济发展水平均在一阶条件下才保持平稳。

表3 面板数据平稳性检验

已有研究对于门槛变量的选择主要有两种方法：（1）通过理论分析框架确定门槛变量对研究对象进行分组［11］。（2）通过门槛效应模型自动识别数据内生特性，利用被解释变量与其影响因素的相关系数来确定门槛值以代替外生分组，从而对样本进行有效划分［12］。为克服传统分组标准的随意性和主观性，本文选取第二类方法确定待检分组门槛变量，通过对待检分组门槛变量的显著性进行分析以确定分组门槛变量。由表4，可以发现在影响农业全要素生产率中最大的两个因素是农业科技资源总错配指数与农业信息化程度分别为0.1213、0.099 7。故依据农业科技资源总错配指数作为门槛分组变量。

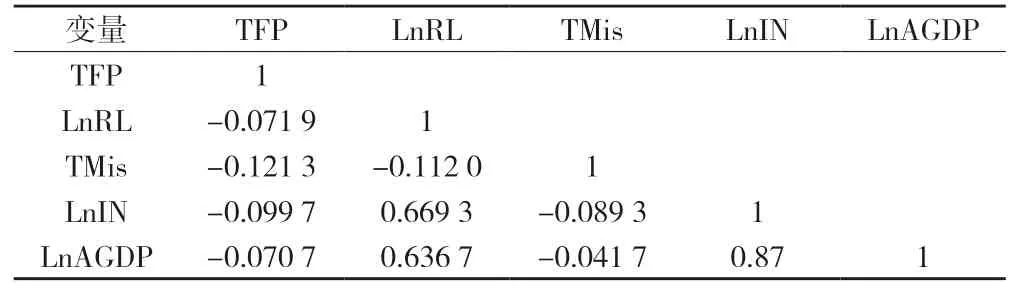
表4 变量相关系数矩阵

本文主要分析农业科技资源错配与全要素生产率的非线性关系，以农业科技资源错配作为门槛变量采用stata14.0 对数据进行回归，通过“自抽法”(Bootstrap)重复抽样500 次获得。回归结果如表5，可知以农业科技资源总错配指数作为门槛变量时，对应的F 值均通在一门槛、二门槛模型都通过了显著性检验。因此，模型中存在两个门槛值，本文选择双重门槛模型进行计量。

表5 门槛效应检验结果

由表6 可以看出具体的两个门槛估计值以及相对应的95%置信区间。因此可以根据两个门槛值数据将我国各省区划分为低错配（Misa＜0.452 2)、中错配(0.452 2＜Misa＜1.762 3)和高错配(Misa＞1.762 3)三个区间。

表6 门槛估计值及置信区间

2.3 模型稳健性检验及结果

为了检验模型的稳健性，采用模型一、二、三分别回归，结果如表7 所示，模型一为没有加入控制变量的单一门槛回归模型。模型二为加入控制变量的单一门槛回归模型。模型三为不考虑门槛效应的固定效应模型。从模型一可知当农业科技资源总错配指数小于0.455 2 时，农业科技资源总错配指数对于农业全要素生产率的影响系数为0.178 且在10%的水平上显著，当农业科技资源错配总指数大于0.455 2 小于1.762 3 时影响系数将为-0.107 且在5%水平上显著，表明此时的农业科技资源总错配指数对于农业全要素生产率的增长具有抑制作用。当农业科技资源总错配指数大于1.762 3 时影响系数为-0.311 且在1%水平上显著时表明农业科技资源错配在大于1.762 3 这个区间对农业全要素生产率的增长也有抑制作用。模型二加入控制变量后农业科技资源错配对于农业全要素生产率的影响程度有一定的提升，但在跨过0.455 2 门槛值后在1%水平上呈反向抑制作用。模型三是固定效应模型从回归系数上看农业科技资源错配对于农业全要素生产率的增长具有抑制作用。说明三种模型中农业科技资源错配对农业全要素生产率的影响系数和显著性差异程度不大，包含控制变量的单一门槛回归模型具有一定的稳健性，且拟合系数最高，可以采用。因此重点分析模型二。

模型二中，在以农业科技资源错配misait 为门槛变量的双重门槛模型中，当农业科技资源总错配指数小于0.452 2 时，其对农业全要素生产率影响的系数为0.238 7，且在5%水平上显著。由此可以看出当农业科技总资源错配较小时，会显著提高农业全要素生产率，但是一旦农业科技资源错配总指数跨过0.452 2 的门槛值时，其对农业全要素生产率的影响系数下降为-0.815 9 且在1%水平上通过了显著性检验，影响作用方向也从正效应变为负效应。随着农业科技资源总错配指数的增大，二者关系呈现一种明显的U 型曲线关系；当农业科技资源总错配指数继续提高以至于超过1.762 3 第二个门槛值时，农业科技资源总错配指数对农业全要素生产率的影响效应依然为负，由于边际效应递减的原理其影响系数已经下降到-0.022，但是依然在1%的水平上显著，说明农业科技资源错配对农业全要素生产率之间存在门槛效应，其效应呈现由“正效应-负效应”的变化趋势。为什么农业科技资源错配指数在不同的错配情况下对于农业全要素生产率的影响有显著差异呢？其内在原因是当农业科技人力、财力资源错配程度较小时还不足以影响农业全要素生产率的变动，但当农业科技人力、财力资源的错配达到一定阈值时导致资源不能被合理的利用进而不能很好的将农业科技资源转化为农业科技产出进而会导致农业全要素生产率的下降。

控制变量对农业全要素生产率影响存在显著差异，农业信息化水平和农村生产力发展水平均在1%水平上显著，且农村生产力发展水平对农业全要素生产率的系数为正，表明农村生产力发展水平的提升对于农业全要素生产率的增长具有促进作用。但农业科技活动人员素质和农业信息化程度对农业全要素生产率的系数为负，表明农业科技活动人员素质和农业信息化水平的提高对于农业全要素生产率的增长具有抑制作用，这说明农业科技劳动投入对于农业全要素生产率的增长有限，甚至在某种程度上会产生负向作用［13］。农业信息化程度对农业全要素生产率产生负向作用，主要是由于农业人力资本未达到相应的水平时不能充分利用农业信息使之转化为科技成果，进而不能有效地促进农业全要素生产率的提升。

表7 面板门槛模型回归及稳健性检验结果

2.4 门槛值的区域差异

从各省市农业科技资源错配情况来看，根据门槛效应的检验结果，总样本存在两个农业科技资源总错配门槛，为了直观反映区域异质性，把1999—2017 年25 个省份总样本最终划分为三个性质不同的子样本，分别为组1（Misait＜0.452)、组2（0.452＜Misait＜1.76）、组3（Misait＞1.76）分组结果见表8，可知处于相对最优的中错配区间（0.452＜Misait＜1.76）样本数总体上所占比例相对较大，占总数的43.78%；处于高资源错配区间（Misait＞1.76）样本数占比最大，占总数的53.89%。表明近几年我国农业科技资源错配虽然有一定的改善趋势，但效果并不是十分明显。

表8 1999—2017 年我国25 个省份农业科技资源错配相对门限值分布情况 单位：组

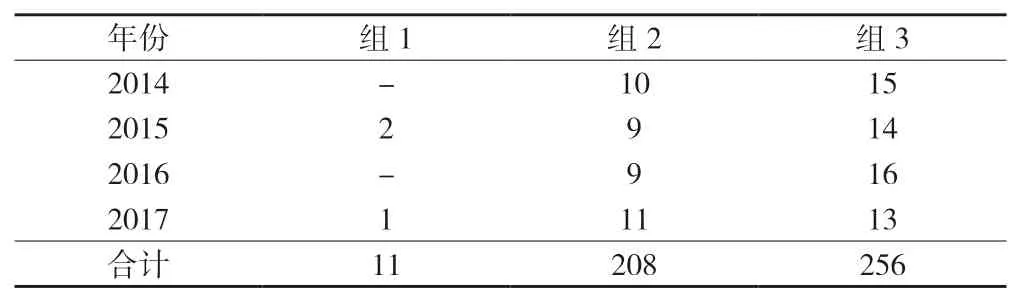
表8 （续）

3 结论与启示

本文根据可获性省级面板数据以农业为例运用DEA 非参数法测度了农业全要素生产率及其变化，并通过门槛效应模型研究农业科技资源错配对全要素生产率的非线性关系，通过实证检验可以得出以下结论：

（1）我国25 个省级农业科学院存在着不同程度的农业科技资源错配情况，经济较为发达地区由于农业科技活动人员与农业科技活动经费的大量积聚造成经济发达地区存在农业科技人力、财力资源存在过剩情况，对于经济后发地区西南地区、西北部地区资源错配程度较为严重，具体表现为农业科技财力资配置过剩和农业科技人力资源配置不足等现象。

（2）农业全要素生产率的提升显著受限于地区农业科技资源错配程度的影响。总体而言，随着农业科技资源错配不断跨越门槛值，农业科技资源错配对农业全要素生产率的影响作用由正变负。同时，根据门槛等级将地区划分为农业科技资源低错配区间、农业科技资源中错配区间和农业科技资源高错配区间三种类型。在低资源错配区间（Misait＜0.452)，农业科技资源错配程度较轻，可以显著促进农业全要素生产率的提升，而在高资源错配区间（Misait＞1.76）,农业科技资源错配在很大程度上会抑制农业全要素生产率的提升。

根据研究结论，优化农业科技资源配置，提高农业全要素生产率可以从以下几个方面努力：（1）完善中国科技资源配置体系，不仅要从宏观上掌握科技资源配置整体状况，还要在微观上关注资源配置能力水平。（2）在农业科技人力资源方面，创造科研人员适宜发展的环境，培养多样化的科技人才，加强地区之间的人才流动以便实现农业科技活动人员之间的优势互补，为了更好的让科技活动人员投入到科研活动中应该完善科技环境和体制；在农业科技财力资源配置方面，加强政府对于资金的管理力度，切实落实一体化改革实现资金最优配置，通过加强产学研合作消除农业科技人力、财力资源之间存在的障碍［14］。（3）加强区域联动，合理引导农业科技资源有序配置转移，实现优势互补进而减少农业科技资源的错配，提高农业全要素生产率。持续深入优化中西部地区的农业科技环境，加强农业科技活动人员的引进工作，改善农业科技人力资源配置不足的现状。