基于改进状态观测器的轧机扭振抑制策略

周红星，李园园，马志强，魏立新，徐德树

（1.浙江富日进材料科技有限公司，浙江 杭州 311106；2.燕山大学工业计算机控制工程河北省重点实验室，河北 秦皇岛 066004；3.天津电气科学研究院有限公司，天津 300180）

轧机主传动系统主要由电机、连接轴、联轴器以及轧辊组成。联轴器因低刚度特性可导致轧机产生扭转振荡[1]。扭振现象可导致系统不稳定甚至机身断裂，引发事故并造成巨大经济损失[2]。

为此，国内外学者提出多种控制方法。例如，为了解决模糊逻辑控制器在抑制扭振方面效率不佳、参数不易调整等问题，文献[3]利用遗传梯度算法优化调整模糊控制器，但不能实现低速调控和非线性控制。文献[4]认为基于神经网络的自适应滑模控制结构可实现非线性控制并能克服抖振现象，提高系统鲁棒性。文献[5]利用转矩前馈抑制低频振动，但此结构不能构建额外反馈回路。为抑制弹性轴振动，需实时测量轧机系统所有状态构成轧辊转速和连接轴转矩反馈回路，保证系统稳定，观测器可以解决此问题。文献[6]提到采用LQ（linear quadratic）状态观测器，响应迅速，系统稳定，但当出现非零干扰转矩时，效果并不理想。文献[7]使用移动水平估计（moving horizon estimation，MHE）对二惯量系统重构状态变量，但在运算过程中存在权重选择困难、计算难度大等问题。神经网络观测器可实现复杂非线性逼近，但运算量巨大，参数不易调节[8]。此外，文献[9]提出状态空间速度控制，通过增加预滤器改进其控制机构。在此基础上，文献[10]改进观测器并提出改进龙伯格观测器（modified luenberger observer，MLO），可在宽速范围内抑制扭振，但该补偿矩阵及增益矩阵中参数多，采用经验选择参数，不具普适性。文献[11]提出ADALINE速度控制器，对抑制轧机扭振有良好效果，但结构单一，仅能控制电机转速与轧辊转速平衡，不能增加额外反馈状态。

抑制弹性轴振动，需获得所有状态变量，增加额外反馈以保证系统稳定，但轧机控制系统复杂，参数不易测量。本文针对以上问题对控制系统做如下改进：首先，为了增加额外反馈和抗干扰能力，引入一种含有积分状态的反馈控制结构；其次，为了提高观测精度，利用多重ADALINE算法改进观测器，实现参数在线观测及调整；最后，基于转速同步思想，在加速度层面设计同步控制器。仿真验证该方法的有效性，并与ADALINE速度控制器及无同步控制下多重ADALINE改进后控制结构进行比较。

1 轧机机电耦合控制系统模型

1.1 轧机机电耦合动力学模型

轧机主传动系统是由若干个惯性元件（包括电机、轧辊等）和弹性元件（连接轴等）组成的“质量弹簧系统”[12]，为便于分析轧机系统性能及控制方法，将轧机主传动系统简化为通过弹性轴连接交流异步电动机与轧辊的二惯量系统，忽略连接轴阻尼[13]，如图1所示。

图1中，Te，Ts，TL分别为电动机电磁转矩、连接轴转矩和轧辊负荷转矩，N⋅m；Jm，JL分别为电机转动惯量、轧辊转动惯量，kg·m2；ωm，ωL分别为电机角速度、轧辊角速度，rad/s；θm，θL分别为电机旋转角度、轧辊旋转角度，rad；Ks为弹性轴刚度系数，N ⋅m/rad。

图1 二惯量系统结构图Fig.1 Structure of a two-inertia system

根据Lagrange原理，建立轧机主传动系统机电耦合非线性动力学方程并转化为机电耦合状态方程，轧机机电耦合数学模型如下式所示：

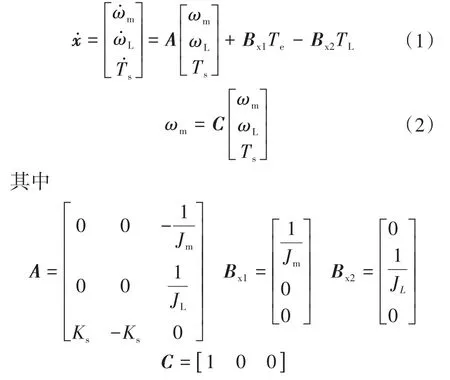
式中：C为输出系数；A，Bx1，Bx2为系数矩阵；x为系统输入。

1.2 积分反馈控制

由式（1）和式（2）可知，状态观测器需要转速和转矩反馈，但是从自由度方面考虑，传统PI控制器的普通级联结构不能有效地抑制扭振[14]，同时也不能选择状态变量，增加额外回路，如图2所示。为此，需要变换控制结构，来增加反馈状态。

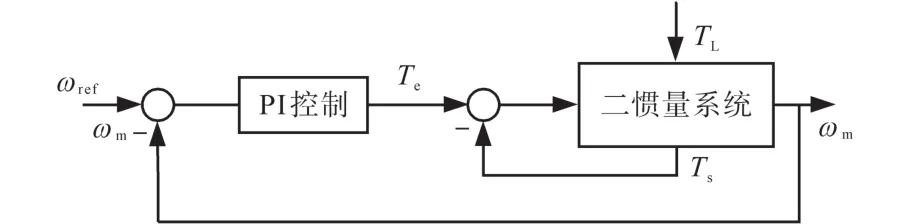
图2 PI控制器的普通级联结构图Fig.2 Common cascade structure diagram of PI controller

反馈控制器能降低干扰对系统的影响[15]，在反馈控制器中引入积分状态，通过配置系统期望极点，可获得多个反馈状态，形成积分反馈控制模型，以达到增加额外反馈状态的目的。设计规则如下：引入积分状态，来降低负荷转矩TL的影响，积分状态可由电机转速差来表示，通过引入反馈矩阵来自由选择闭环极点，可表示为

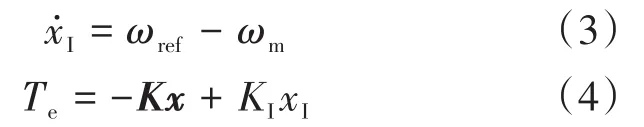
式中：xI为积分状态；ωref为给定电机速度；K为反馈增益矩阵；K1为积分系数为xI的一阶导数。

配置期望极点，增加转速、转矩反馈回路，反馈系统表示为

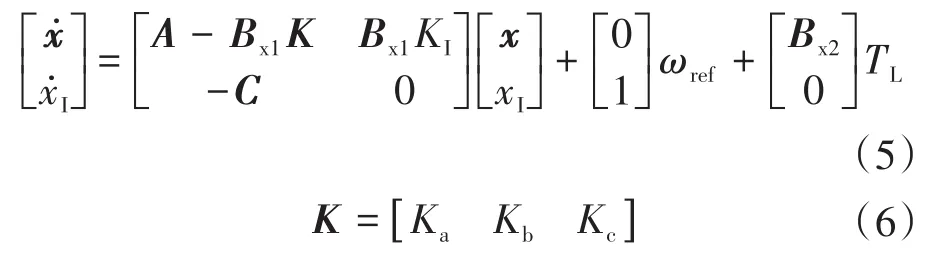
系统期望的特征方程为

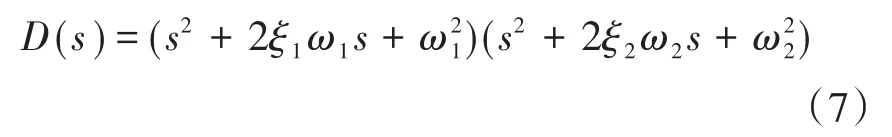
式中：ω1，ω2为谐振频率；ξ1，ξ2为阻尼系数。

由式（7）可知反馈增益为

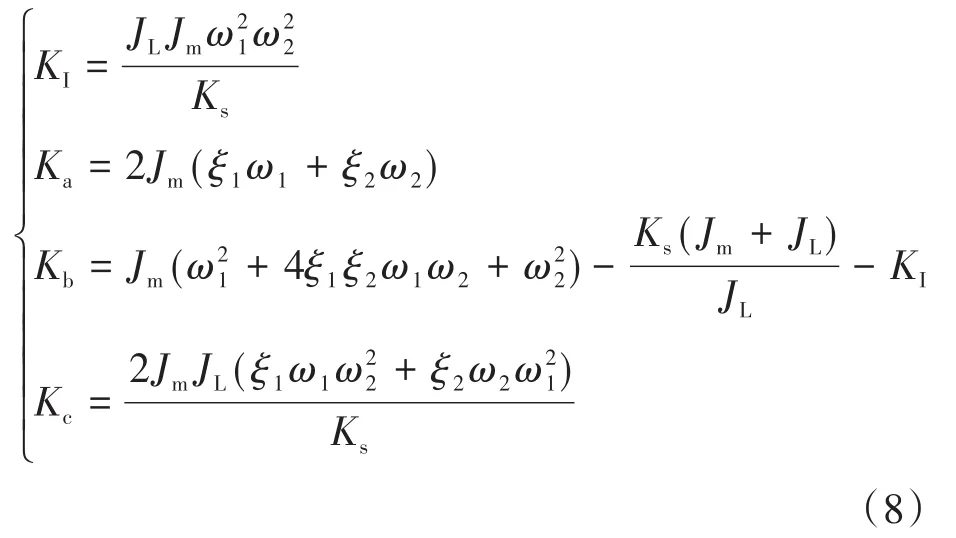
由式（1）～式（8）可得轧机机电耦合控制系统结构如图3所示。与图2相比，增加了转速和转矩控制回路，避免现场实时测量参数；反馈参数可由控制规则获得，避免参数调整；同时，积分状态可降低非零干扰的影响。

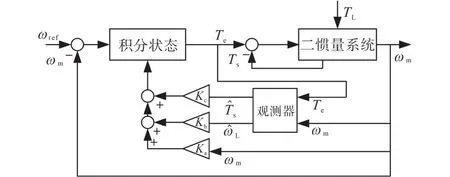
图3 轧机机电耦合控制结构图Fig.3 Structure of electromechanical coupling control for rolling mill

系统稳定性证明如下：

由式（7）知期望特征方程为

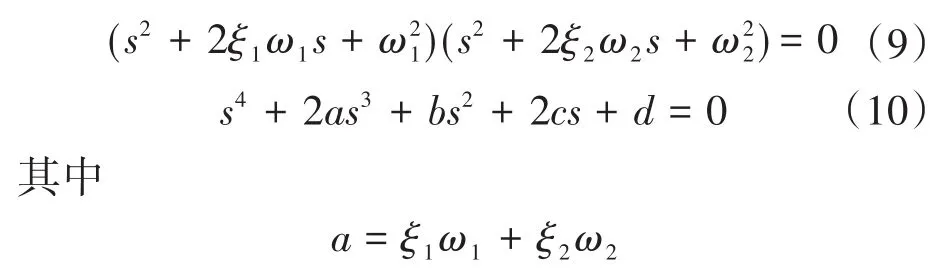
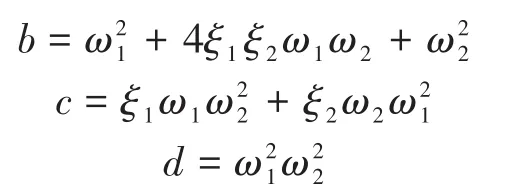
式中：a，b，c，d为保证系统稳定时的系数。

为保持系统稳定，根据赫尔维茨稳定判据，式（10）中的各系数应满足：

即a＞0,ad-c＞0,abc-c2-a2d＞0,d＞0,b＞0,c＞0,bc-ad＞0，且b2-4d＞0。

由式（11）和以上条件可得：

当取ω1，ω2，ξ1，ξ2取值满足式（12）时，系统稳定。

2 多重ADALINE状态观测器

2.1 状态观测器

由于轧机系统参数不易测量，需实时获得轧辊转速和连接轴转矩状态，可通过状态观测器实现，可获得系统所有状态且自由选择所有闭环极点。为了提高观测器的精度，状态观测器方程设计如下：

观测器的状态方程为

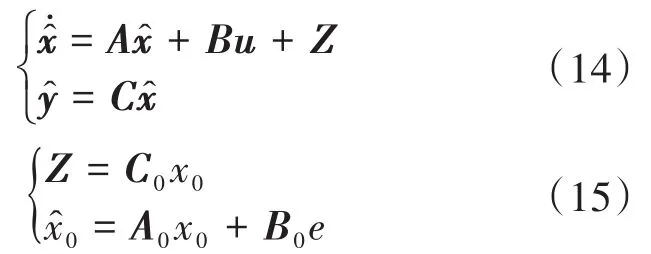
式中：A，B，C为常数矩阵；u为输入矢量；x为系统状态量；“^”代表估计量；y为输出矢量；x0为误差状态变量；A0，B0，C0为观测矩阵；Z为输入误差；e为系统输出误差。e定义为

式（1）、式（14）、式（16）经拉普拉斯变换可得：

式中：I为对角为1的矩阵。

式（15）经拉普拉斯变换得：

式中：G(s)，H(s)为输出矩阵；C0为观测矩阵。

2.2 多重ADALINE算法改进观测器

ADALINE自适应调节可使ADALINE速度控制器保证电机转速与轧辊转速一致[16]，但控制变量单一。H(s)随系统调节而变化，普通状态观测器在参数恒定、非线性较低的控制系统中效果不错，但面对参数多变、非线性复杂的传动系统，效果不理想[17]。

因此，由多重ADALIN算法改进状态观测器[14]，避免多个观测量间相互耦合作用，降低反馈误差，实现H(s)在线补偿，保证系统稳定。单重ADALINE控制器[15]通过自适应算法调整非线性状态及一个激活函数来处理输出，结构如图4所示。

图4 ADALINE结构图Fig.4 ADALINE structure

输入信号及误差信号用一个低通滤波器代替延迟元件形成扩展后的输入适量模块。输入x1，x2，x3，x4与权重W1，W2，W3，W4分别相乘并求和，得到y，非线性激活函数代替线性激活函数为

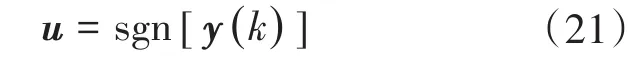
自适应算法为

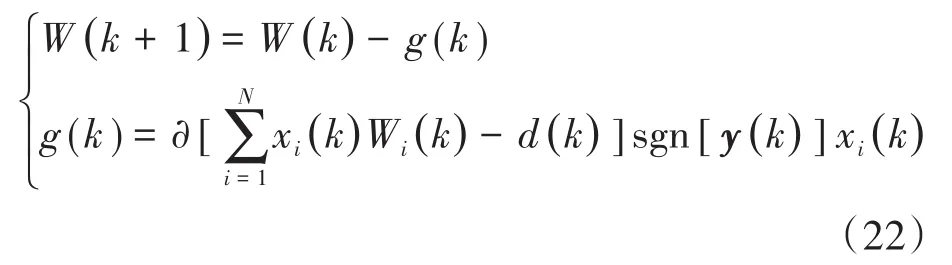
式中：d(k)为第k次迭次过程中期望的输出；xi为第i个输入信号；N为输入信号的总个数；W(k+1)，W(k)分别为第k+1和第k次权重；∂为学习率；k为迭代次数。

单个ADALINE控制器控制过程如下：

1）初始化第1代权重，取随机值；

2）获得处理过的输出信号；

3）计算误差信号；

4）自适应算法求新的权重系数，该训练模式降低输出误差，训练学习率，得到期望控制信号。

H(s)可通过增益k1，k2，k3调节多重 ADALINE的输出获得，如图5所示。其增益可提前利用优化算法择优选择，避免控制初期出现较大波动。优化算法的适应度函数采用误差函数ITAE，如下式所示：

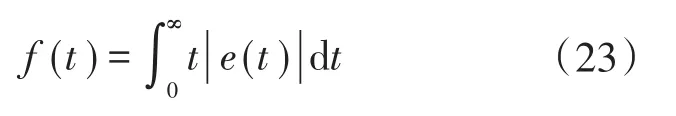
式中：e（t）为电机转速误差。

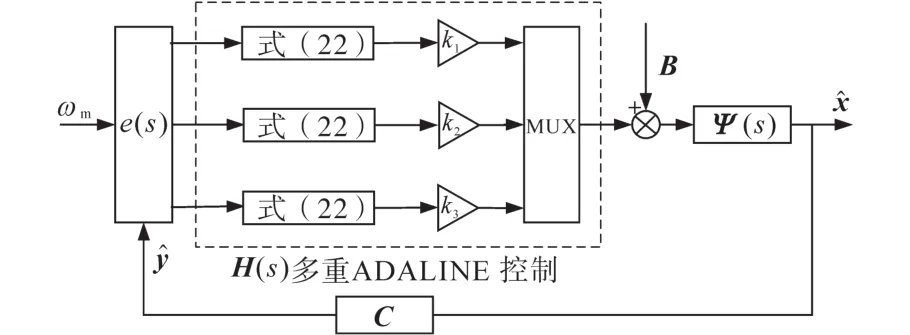
图5 多重ADALINE状态观测器结构图Fig.5 Structure diagram of multiple ADALINE state observers

3 同步控制

连接轴发生扭振时，电机速度可能与轧辊速度不同。为此，可采用同步控制[18]思想来平衡电机和轧辊转速，为实现电机转速和轧辊转速同步，在加速度层面对同步控制器进行设计，控制目标为

对速度和旋转角度的控制，可实现加速度控制，加速度控制表示为

式中：us，up分别为速度、旋转角度控制量。

速度控制以速度和为反馈对象，控制目标为2ωref，旋转角度控制以旋转角度差为反馈对象，控制目标为0。

为了便于分析，速度控制采用PI控制，旋转角度控制采用PD控制，可表示为[18]

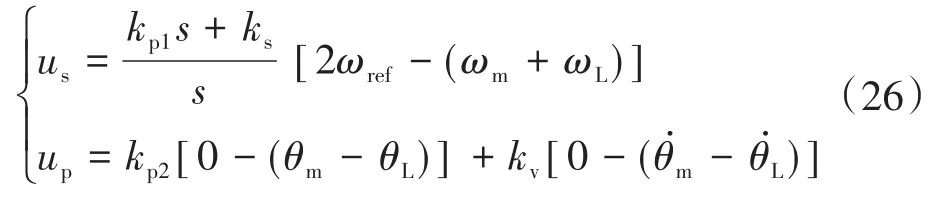
式中：kp1，ks，kp2，kv为控制器的系数；θm为电机转动角度；θL为轧辊转动角度为电机转动角速度为轧辊转动角速度。

综上所述，改进后轧机机电耦合控制结构如图6所示。

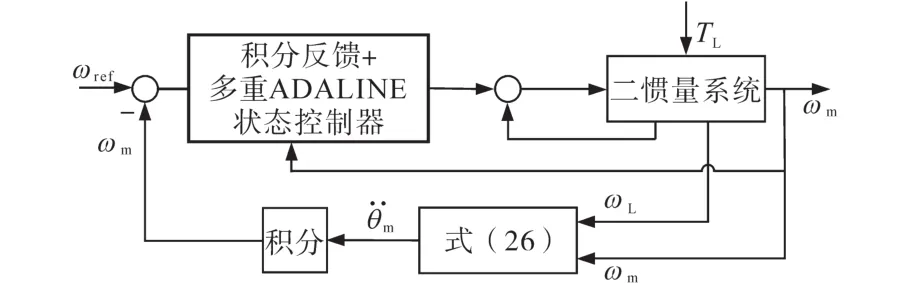
图6 机电耦合控制结构图Fig.6 Electromechanical coupling control structure

4 仿真验证

为了验证所提控制结构的正确性，采用文献[10]研究的数据进行仿真验证，系统参数为：电机转动惯量Jm=0.001 kg·m2，负载转动惯量JL=0.0036kg⋅m2，弹性轴刚度系数Ks=1.27N⋅m/rad，ADALINE算法通过编写S函数实现，控制系统如图6所示。

首先，通过粒子群算法进行寻优，获得增益k1，k2，k3，在宽速范围内进行仿真验证；并与ADALINE速度控制器以及多重ADALINE观测器相比较，对比结果如图7～图10所示。

图7 给定电机转速曲线图Fig.7 Given motor speed graph

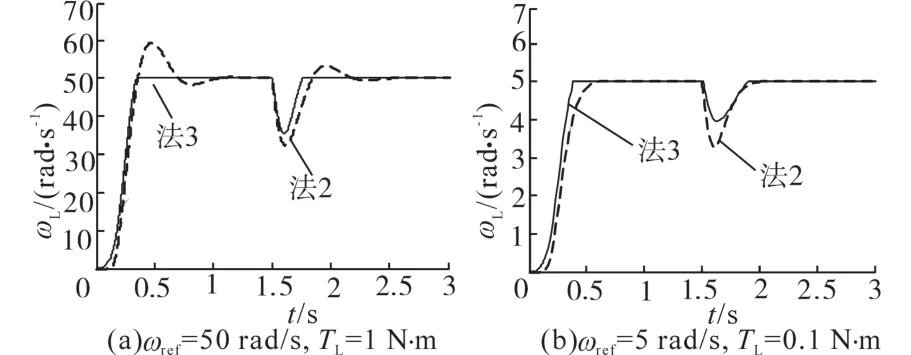
图8 轧辊转速曲线图Fig.8 Roll speed graph

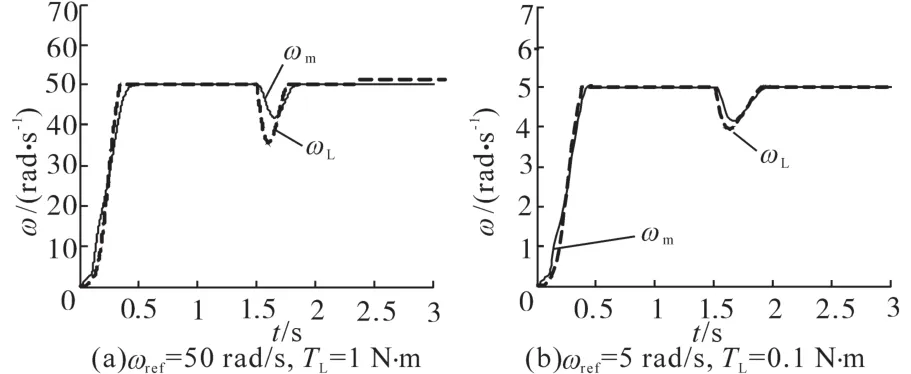
图9 同步控制下电机，轧辊转速曲线图Fig.9 Roll speed graph of motor under synchronous control

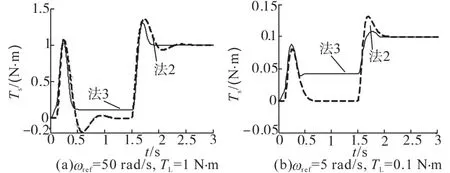
图10 连接轴转矩曲线图Fig.10 Connecting shaft torque graph

轧机轧制过程中，当电机处于低速状态下，轧辊咬钢。在t=0.1s时，给定系统一个ωref=50 rad/s的阶跃信号，模拟轧机系统启动过程，在t=1.5s时，给定系统一个TL=1 N·m的阶跃信号模拟轧机系统起振过程，仿真结果如图7a～图10a所示。在t=0.1s时，给系统一个ωref=5rad/s的阶跃信号，模拟轧机系统启动过程，在t=1.5s时，给系统一个TL=0.1N⋅m的阶跃信号模拟轧机系统起振，结果如图7b～图10b所示。

由图7a可知，启动时，较ADALINE速度控制器（法1）和多重ADLINE状态反馈控制（法2），同步控制器状态反馈控制（法3）的电机转速曲线调节时间最短，在0.5 s前达到稳速，相较法1曲线较平滑，相较法2无超调。起振过程中，法3与法1相比，ωm幅值降低37.31%，与法2相比，幅值降低19.49%；法3调节时间为0.37 s，较法1用时短，较法2用时略长。

由图8a可知，在控制初期，法3控制的曲线调节时间较短且无超调；起振时期，法3相较法2幅值降低17.54%且调节时间较短。由图9a可知，法3对ωm和ωL的控制情况，起振时期，ωL与ωm相比振幅较大，表明扭振对轧机影响较严重。

由图10a可知，控制初期，连接轴转矩经法3控制调节时间短，起振时期，法3较法2，连接轴转矩振幅降低11.86%。

由图7b～图10b可知，在轧机系统运行时，法3控制性能较好。由各图a、图b对比可知，法3可在宽速范围内抑制轧机扭振。

为进一步表明所提方法的抑制扭振的效果，取图7a、图9a中时间在1.5～3 s的数据作幅频图，如图11所示。

由图11a可知，0频时，电机转速均有直流分量，法1控制的电机转速ωm直流分量较小。但当频率大于0时，其控制下幅值最大，振动最强烈。相比较，法3控制的电机转速ωm振幅较小，即扭振程度较弱，抑振效果较好。图11a中，在15.3 Hz，23.5 Hz，32.5 Hz处出现峰值，振动表现为以频率15.3 Hz的1倍频、1.5倍频、2倍频震荡。由图11b可知，电机和轧辊出现同频振动，ωL振幅较大，即轧辊振动较严重，表明扭振对轧辊的影响较大。

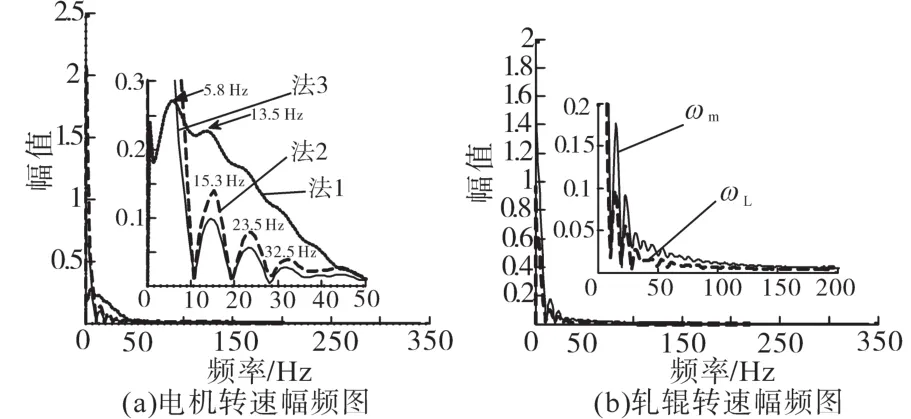
图11 电机转速、轧辊转速幅频图Fig.11 The amplitude frequency diagram of motor speed and roller speed

由于增加同步控制器，在调控系统时，状态反馈系数出现小范围变化。不同ωref，KI，Ka下ωm曲线如图12、图13所示，各反馈系数下ωm控制规律如表1所示，以分析反馈系数对系统的影响。

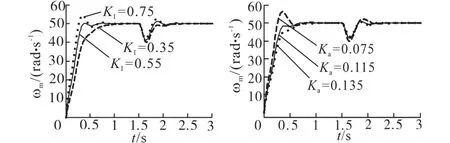
图12 不同KI，Ka下电机高速曲线图Fig.12 DifferentKIandKacontrol of motor high speed graph

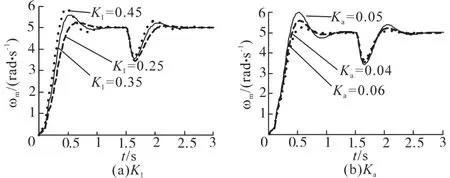
图13 不同KI，Ka下电机低速曲线图Fig.13 Motor low speed graph under differentKIandKacontrol

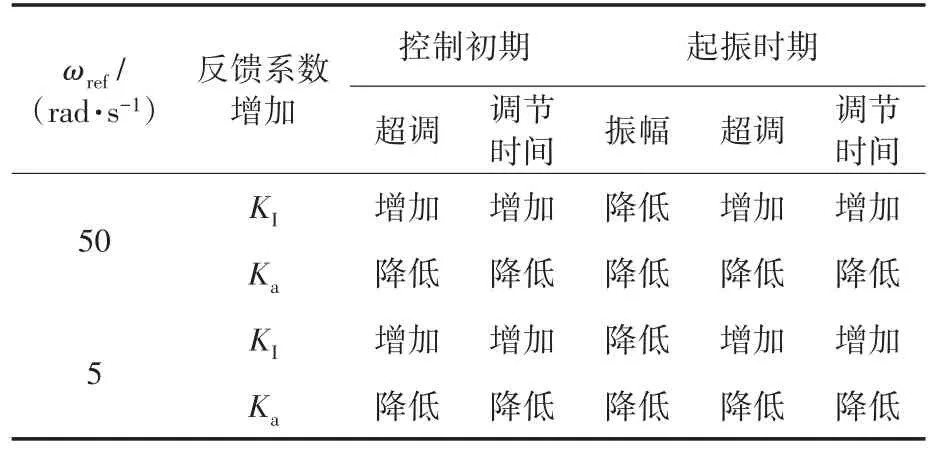
表1 不同反馈系数下电机转速控制规律Tab.1 Motorspeedcontrollawunderdifferentfeedbackcoefficients

由表1可知，同一反馈系数下不同ωref对ωm的控制规律相同，同一ωref下不同反馈系数对ωm超调和调节时间的控制有所不同。

通过仿真对比可知，与ADALINE速度观测器和仅改进状态观测器两种控制结构相比，增加同步控制器在宽速范围内降低扭振幅值且调节时间短，可有效抑制轧机扭振，提高轧机主系统稳定性。

5 结论

针对联轴器刚度低及突加干扰下轧机主传动机电耦合系统出现扭振情况，考虑到轧机系统强耦合、强非线性及参数不易测量等特点，做以下工作：

1）引入积分状态，增加额外反馈，由极点配置获得反馈参数，保证控制系统稳定。

2）利用ADALINE算法改进观测器，设计多重ADALINE状态观测器，提高观测精度，用优化算法优化增益控制变量，避免控制初期不稳情况。

3）设计同步控制器，以平衡电机转速、轧辊转速来降低调节时间。

4）最后通过仿真对比验证，表明所提出方法在降低振幅、减少调节时间方面控制效果良好。