基于拓扑优化的矿用排岩机箱体式履带设计

矿山采掘装备及智能制造国家重点实验室 山西太原 030024

矿用排岩机的履带既是整机的行走机构，又是整机的承载机构。为了保证矿用排岩机在各类复杂工况中安全稳定运行，其接地比压不能超过排岩场允许的接地比压。以往常规的履带多为铸件结构，但铸件笨重、缺陷多、废品率高，给生产制造和用户准备备件带来极大的困难。

目前，随着拓扑优化技术的快速发展，其已被广泛应用于结构设计当中[1]。拓扑优化设计方法能在工程结构设计的初始阶段，为设计者提供一个概念性设计方案，使结构在布局上达到最优，从而改变了以往的设计、校核、修改不断反复的开发流程[2]。与尺寸优化和形状优化相比，拓扑优化能够得到更大的经济效益，被认为是一个更具有挑战性的领域，已经成为当今结构设计研究的一个热点[3]。

因此，笔者提出一种新型箱体式履带，并采用拓扑优化设计方法，设计出其内置加强肋，然后对该设计进行力学性能分析，验证其合理性和有效性[4]，最终设计出了一种内置拓扑加强肋的新型箱体式履带。

1 拓扑优化数学模型的建立

在对连续体结构进行拓扑优化时，变密度法是最常用的方法之一，在此笔者采用变密度法对箱体式履带进行拓扑优化设计。变密度法的基本思想是人为假设材料单元的密度是可变的，并假设这种材料单元的密度与材料的物理属性之间存在某种函数关系。根据以上假设建立材料模型，以材料密度的分布情况来确定结构材料的布局情况[5]。但在使用该方法时会出现大量的中间密度材料单元，这显然是不希望看到的，因此通过 SIMP 法引入惩罚因子p，使材料的中间密度值向 0 和 1 两端聚集，从而得到最终的优化结果。

结合载荷与位移边界条件，可得到基于 SIMP 法的结构拓扑优化模型为

式中：ρ为拓扑设计变量；Xi为每个单元的相对密度，当Xi=1 时，保留结构的材料，当Xi=0 时，去除结构的材料；ρi为每个单元的固有密度；Ki为每个单元的刚度；Ki为每个单元的固有刚度；p为惩罚因子。

以箱体式履带总体柔度最小为目标函数，则机械臂壳体的拓扑优化数学模型[6]为

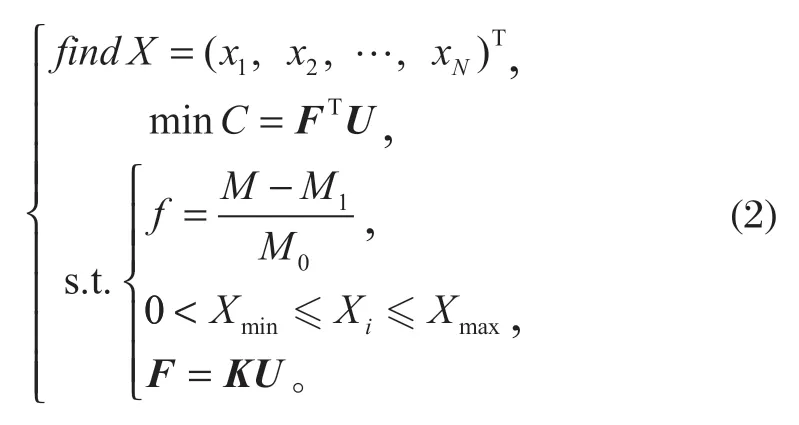
式中：目标函数C为机械臂壳体的总体柔度；F为载荷矢量；U为结构位移向量；K为优化前结构总刚度矩阵；M为充满材料的体积；M0为结构设计域的体积；M1为密度小于 1 的材料体积；f为剩余材料百分比；Xmin为单元相对密度的下限；Xmax为单元相对密度的上限。

2 箱体式履带拓扑优化设计

2.1 静力学分析

在进行静力学分析之前，需要先对履带进行适当简化：①清理掉一些不会影响分析结果的工艺孔和倒圆角等；② 由于箱体式履带为对称结构，为了便于计算和提高效率，取其中一侧，并去掉中间连接部分；③为了探寻箱体式履带内置肋板的结构，将箱体式履带内部填充实体，以便进行拓扑优化。使用SolidWorks 构建的原始箱体式履带模型如图 1 所示。

该箱体式履带采用的材料是 Q345 结构钢，弹性模量E=2×105MPa，泊松比µ=0.3，密度ρ=7.85×103kg/m3。采用 ANSYS Workbench 智能网格划分技术对该模型进行网格划分，单元大小为 20 mm，共得到 95 948 个节点和 29 686 个单元。

图1 原始箱体式履带模型Fig.1 Model of original boxed crawler

对箱体式履带一侧与连接部分接触面处施加固定约束 (Fixed Support)，对箱体式履带底部施加 0.11 MPa 压力 (Pressure)，如图 2 所示。

图2 箱体式履带载荷和约束Fig.2 Loads and restraints of boxed crawler

图3 箱体式履带静力学分析结果Fig.3 Static analysis results of boxed crawler

静力学分析结果如图 3 所示。对箱体式履带进行静力学分析求解运算后可得：箱体式履带的最大应力为 57.62 MPa，位于箱体式履带一侧与连接部分接触面处，如图 3(a) 所示；最大变形为 0.59 mm，位于箱体式履带外侧端，如图 3(b) 所示。可见内部填充实体的箱体式履带的强度与刚度均能够满足实际工作需求；但很大部分所受应力及变形都比较小，材料冗余量较大，存在很大的优化空间。

2.2 拓扑优化设计

笔者在 Static Structural 模块的基础上调用 Topology Optimization 模块对箱体式履带进行拓扑优化。合理有效的参数设置才能得到更佳的优化效果，因此在优化前先对参数进行设置，如表 1 所列。

表1 参数设置Tab.1 Parameter setting

参数设置后进行迭代计算。箱体式履带的拓扑优化结果如图 4 所示，其中黑色部分为原内部填充实体的拓扑优化结果。

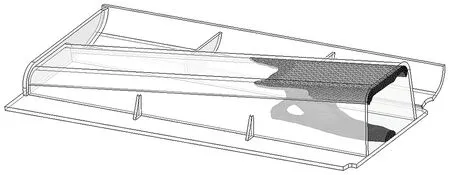
图4 箱体式履带拓扑优化结果Tab.4 Topological optimization results of boxed crawler

根据拓扑优化结果并综合考虑加工制造和装配等因素，对箱体式履带进行重构。重构时保留具有特定作用的部分，重构后的箱体式履带模型如图 5 所示。

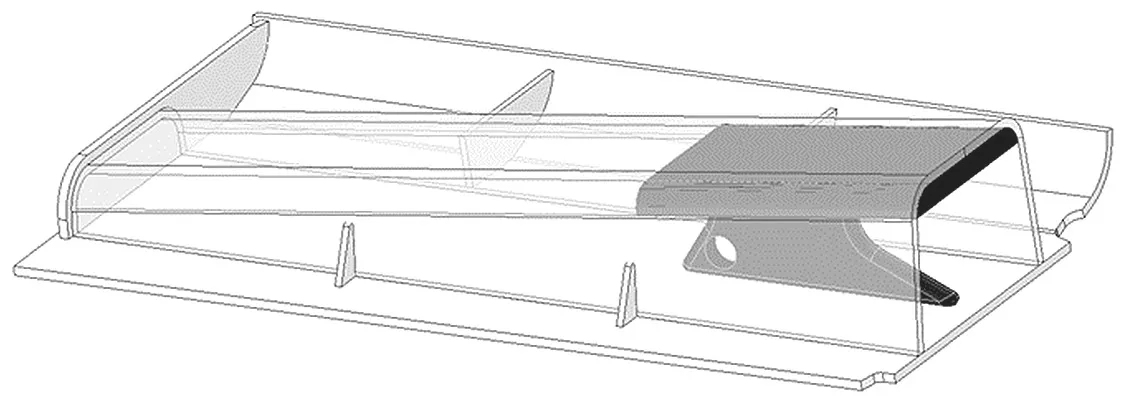
图5 重构后的箱体式履带模型Fig.5 Model of reconstructed boxed crawler

对重构后的箱体式履带模型进行静力学分析，得到应力及变形云图，如图 6 所示。从图 6 可以看出，重构后的箱体式履带最大应力为 109.11 MPa，远小于材料的抗拉强度，最大变形为 1.01 mm，也满足设计要求。此外，传统履带质量为 270 kg，重构后的箱体式履带质量为 254 kg，质量减少 6%。

图6 重构后的箱体式履带静力学分析Fig.6 Static analysis on reconstructed boxed crawler

重构后的箱体式履带整体模型如图 7 所示。结果表明，重构后的箱体式履带满足高承载、高刚度、高强度及轻质量等设计要求，设计出一种内置拓扑加强肋的新型箱体式履带，解决了传统铸件履带笨重、缺陷多及废品率高的问题，并保证其具有低接地比压，以适应排岩场的持续沉降。

图7 箱体式履带重构后整体模型Fig.7 Whole model of reconstructed boxed crawler

3 结论

(1) 为解决传统铸件履带结构的不足，并保证新型履带具有低接地比压以适应排岩场的持续沉降，笔者提出了一种新型箱体式履带，并应用 ANSYS Workbench 对其进行静力学分析，确定了可优化区域；

(2) 采用拓扑优化设计方法，设计了箱体式履带内置加强肋，在保证高承载设计要求的前提下，为箱体式履带的轻量化设计提供了一种科学依据；

(3) 在拓扑优化的基础上，综合考虑加工制造和装配等因素，对箱体式履带进行重构，减轻了箱体式履带的质量，并通过对重构后的箱体式履带进行力学性能分析，验证了该设计的合理性和有效性。