极小负co-location 模式及有效的挖掘算法
王光耀,王丽珍,杨培忠,陈红梅
云南大学信息学院,昆明 650504
随着空间数据信息的爆炸式增长,从大量空间数据中发现有价值的信息成为一项重要的任务。空间co-location(并置)模式是空间特征的一个子集,它们的实例在空间中频繁关联。例如,医院和药店经常并置出现,根瘤菌时常长在豆科植物旁。空间colocation 模式挖掘在地理信息系统、图像数据、公共交通领域等许多带有空间属性的领域中有着非常广泛的应用。
尽管已有大量有关正co-location 模式挖掘的算法,但负co-location 模式挖掘方面的研究成果却是稀有的。原因是负关联规则挖掘、负序列模式挖掘以及正co-location 模式挖掘的算法都难以被简单地运用到负co-location 模式挖掘中,并且挖掘出的负colocation 模式数量具有组合爆炸的特点,因此研究负co-location 模式的挖掘具有极大的难度。
实际上,在空间数据挖掘中,负co-location 模式在许多应用中也是极其重要的,它表现了某些特征之间较少地出现在一起,但它们之间有着较强的负相关性,包含了非常有价值的信息,因此挖掘负colocation 模式具有十分重要的意义。植物学家不仅对共生植被感兴趣,同时对植被的相克关系(负相关性)也感兴趣,在园林设计中,需要注意树种之间的相克关系;在植树造林时,需要充分考虑植被的相克现象才能趋利避害,例如:通过植被数据负相关性挖掘,可得到柏树和苹果树、柏树与榆树具有较强的负相关性;利用植被相克的原理,以植被的汁液为原料,可提取无毒、无残留和无副作用的高效植物除草剂或杀虫剂,例如:通过从植被及动物分布数据中可挖掘到豆芜青与棉花具有较强的负相关性,通过进一步的研究可从棉花中提取相应的化学物质作为对豆芜青的杀虫剂;在养殖业和畜牧业中,考虑动植物间的相克关系,可避免不必要的生病或死亡。
为了提高频繁负co-location 模式挖掘结果的可用性,挖掘出较少的、具有代表性的、可推导出所有频繁负co-location 模式的模式是非常有意义的。因此,本文提出了极小负co-location 模式新概念。
主要贡献包括:
(1)在严格定义负co-location 模式的基础上,分析了负co-location 模式所具有的“向上包含”性质。基于此,提出了极小负co-location 模式新概念,证明了极小负co-location 模式集可推导出所有频繁负colocation 模式。
(2)基于负co-location 模式的“向上包含”性质,提出一个有效的极小负co-location 模式挖掘算法及频繁负co-location 模式的推导算法。3 个剪枝策略的提出,有效地提高了负co-location 模式挖掘的效率。
(3)在真实和合成数据集上进行了广泛的实验,并与现有算法进行了对比,证明了本文提出的算法挖掘出极小负co-location 模式的正确性及高效性。解决了现有负co-location 模式挖掘算法耗时长、挖掘结果数量巨大等问题。
1 相关工作
近年来许多学者对空间co-location 模式挖掘的理论和算法进行了一系列深入的研究,并取得了丰硕的成果[1-9]。文献[1]提出了将最小参与率作为colocation 模式的有趣性度量指标,并给出了一种基于完全连接的频繁co-location 模式挖掘算法;文献[2]提出了一种基于部分连接的算法,减少了完全连接算法中表实例连接的巨大开销;文献[3]提出了一种无连接的算法,基于星型邻居扩展,更好地优化了在表实例的连接过程的开销的问题。
Wang 等人在空间co-location 模式挖掘领域进行了一系列进一步的研究,文献[4]提出了CPI-tree(colocation pattern instance tree)算法,以树形结构物化空间邻近关系;文献[5]提出了iCPI-tree(improved colocation pattern instance tree)算法,进一步优化了基于CPI-tree的挖掘过程。
co-location 模式挖掘当下热点为模糊co-location模式挖掘、并行co-location 模式挖掘、高效用colocation 模式挖掘和带稀有特征的co-location 模式挖掘等。文献[6]提出了一种基本模糊co-location 模式挖掘算法,并提出了基于网格的距离计算和剪枝候选模式两种优化算法;文献[7]使用并行算法挖掘colocation 模式;文献[8]定义了特征在模式中的效用权重,提出了基于特征效用参与率的高效用co-location模式挖掘算法;文献[9]提出了带稀有特征的colocation 高效挖掘算法。
在co-location 模式的紧凑表示研究中,Wang 等人提出了许多有效的方法:文献[10]提出了闭频繁co-location 模式的有效挖掘算法;文献[11]提出了频繁co-location 模式的冗余缩减算法;文献[12]提出了空间极大co-location 模式挖掘算法等。
以上文献虽在co-location 模式挖掘领域进行了大量的研究,但均只适用于正co-location 模式。在负规则的研究中,有许多学者提出了相关的挖掘算法,但多用于关联规则及序列模式的挖掘中。文献[13]中对传统关联进行了扩展,提出了负关联规则的概念,并定义了兴趣度度量,提出了有效的剪枝策略;文献[14]给出了负序列模式的定义和一些约束条件,提出了一种新的挖掘负序列模式的方法;文献[15]提出了一个基于集合理论的负序列模式挖掘的算法e-NSP(efficient negative sequential pattern),该算法无需对数据库进行重新扫描,从而有效地识别负序列模式;文献[16]提出了一种快速的负序列模式挖掘算法(fast negative sequential patterns,f-NSP),使用位图来存储正序列模式的信息。
负关联规则及负序列挖掘的算法适用于事务数据库,而在空间数据库中负模式的研究是稀有的。基于正co-location 模式挖掘的算法,Jiang 等人[17]首次提出了负co-location 模式的概念及负co-location 模式的有趣性度量指标,设计了一个空间正负co-location模式的挖掘算法,称为PNCP(positive and negative colocation patterns)算法,并基于负co-location 模式的向上扩展性对候选负co-location 模式进行剪枝,该算法可挖掘出频繁的正负co-location 模式。根据负colocation 模式参与度的定义,负co-location 模式不具备类似于正co-location 模式的向下闭合性。现有的负co-location 模式挖掘算法中,基于非频繁模式来定义的负模式,导致从数据集中挖掘出的负模式结果数量巨大,在挖掘的过程中极其耗时。用户在数量巨大的频繁负co-location 模式中找出感兴趣的信息是困难的。
基于PNCP 算法挖掘出的频繁负co-location 模式数量巨大且挖掘过程耗时长等问题,本文提出了一个挖掘极小负co-location 模式的有效算法,极小负co-location 为频繁负co-location 模式的一种紧凑表示,可有效压缩挖掘结果,提高挖掘效率。
2 形式化定义及分析
在空间数据库中,不同的空间特征代表不同类型的空间对象,例如某种类型的植被、某种功能的建筑等。给定一个空间特征的集合F={f1,f2,…,fm},每个空间特征都具有一组与其对应的空间实例分布在空间中不同的位置,与F对应的空间实例集合S={s1,s2,…,sn}。其中每个si(1 ≤i≤n)都是由<实例所属特征,实例号,空间位置>三个部分组成。如图1所示的空间实例集中,分别有A、B、C、D四个特征,其中A1 表示特征A的第一个实例。给定一个空间邻近距离阈值d,若实例si和sj(1 ≤i≤n,1 ≤j≤n)的距离小于阈值d,则称实例si和sj满足空间邻近关系R,表示为R(si,sj)。如图1 所示的空间实例集,若两个实例间使用实线连接,则表示这两个实例满足邻近关系R。
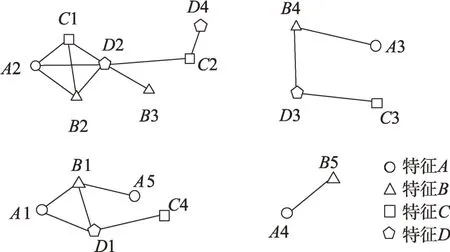
Fig.1 A spatial instance set图1 一个空间实例集
一个空间co-location 模式c是一组空间特征的子集,co-location 模式c的长度称为此co-location 模式的阶,即co-location 模式里空间特征的个数,记作size(c)=|c|,例如{A,B,C}是一个三阶的模式。一个k阶co-location 模式c={f1,f2,…,fk}(c⊆F),一组空间实例的集合I={s1,s2,…,sk}(I⊆S) 且{R(si,sj)|1 ≤i≤k,1 ≤j≤k} 。若I包含了co-location 模式c中的所有特征,并且I中没有任何一个子集可以包含c中的所有特征,那么I被称为c的一个行实例,co-location 模式c的所有行实例的集合称为表实例,记为table_instance(c)。
为了衡量一个空间co-location 模式的频繁性(有趣程度),在co-location 模式挖掘中使用参与度度量一个模式的频繁(有趣)程度,而一个co-location 模式的参与度取决于该模式中各个特征的参与率。在colocation 模式c中,空间特征fi(1 ≤i≤k)的参与率表示为PR(c,fi),它是fi的实例在空间co-location 模式c的表实例中不重复出现的实例个数与fi总实例个数的比率。即:
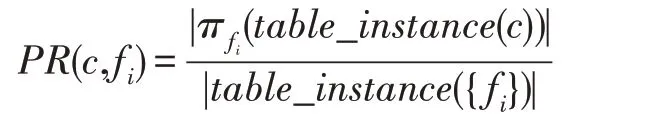
其中,π是关系的投影操作。co-location 模式c={f1,f2,…,fk}的参与度PI(c)是co-location 模式c的所有空间特征的PR值中的最小值,即:
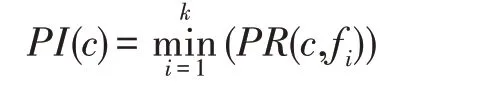
当用户给定一个参与度阈值min_prev,若PI(c)≥min_prev,则称c为频繁的co-location 模式。
例1如图1 所示,包含4 个空间特征A、B、C和D,A有5 个实例,B有5 个实例,C有4 个实例,D有4 个实例。给定参与度阈值min_prev=0.5。co-location模式{A,B}的表实例为{{A1,B1},{A2,B2},{A3,B4},{A4,B5},{A5,B1}},参与度为min(PR({A,B},A),PR({A,B},B))=,则co-location模式{A,B}是频繁的。
引理1(反单调性)参与率(PR)和参与度(PI)随着co-location 模式阶的增大单调递减。
参与率和参与度的反单调性证明可参见文献[18]。给定两个co-location 模式I和I′,模式I′是模式I的子集,即I′⊂I,对于模式I′中的每个特征fi∈I′,都有PR(I′,fi)≥PR(I,fi) 。根据参与度的定义,可得到PI(I′)≥PI(I)。

在非频繁的co-location 模式中,某些特征之间存在着较强的负相关性,而这类模式也具有很大的挖掘价值,例如松树与接骨木,柏树与桔树都具有相克现象。
定义1(负co-location 模式)一个带有负项特征的co-location 模式,称为负co-location 模式,一般记为T=X⋃,X是正项特征的集合,是负项特征的集合,且≥1,X⋂Y=∅。
若一个co-location 模式中不含有负项特征,则称该模式为正co-location 模式。
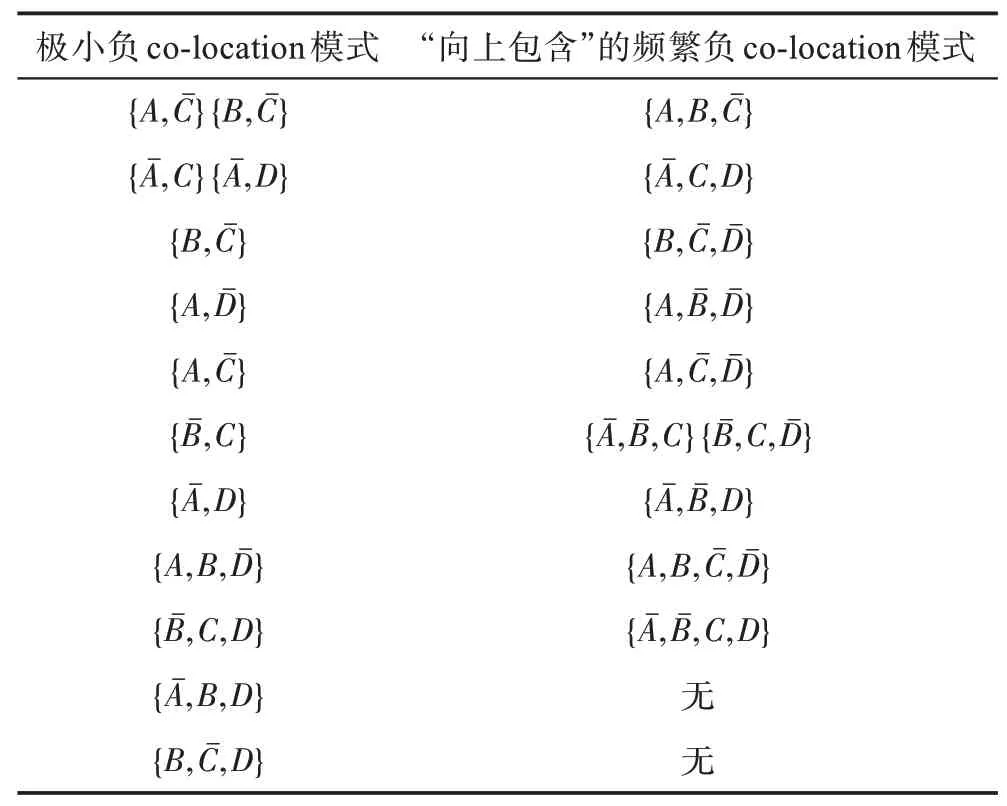
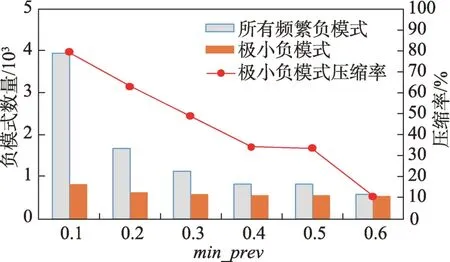
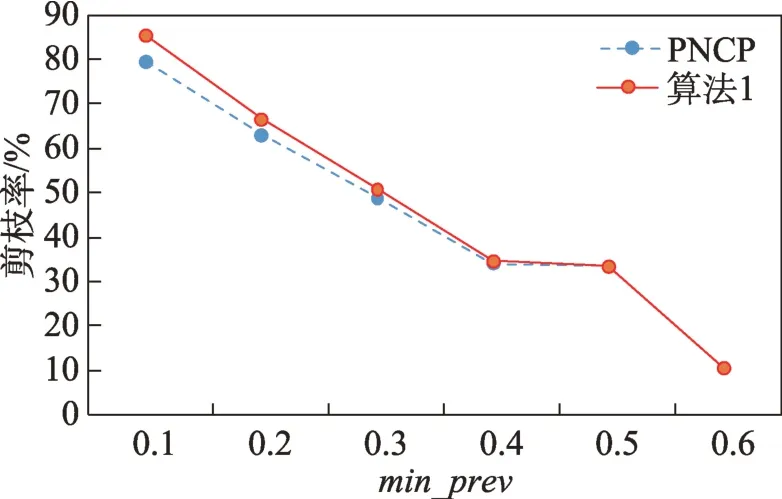
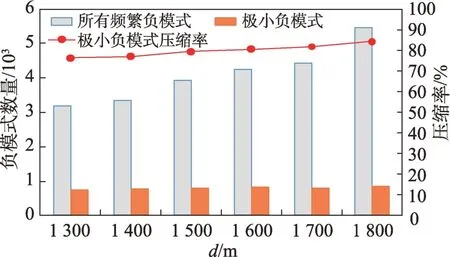
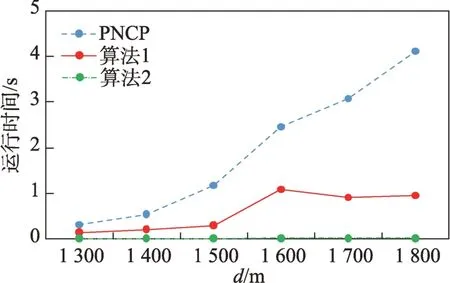
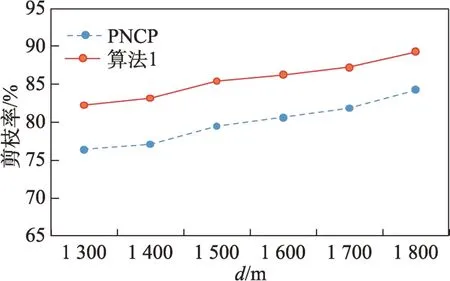
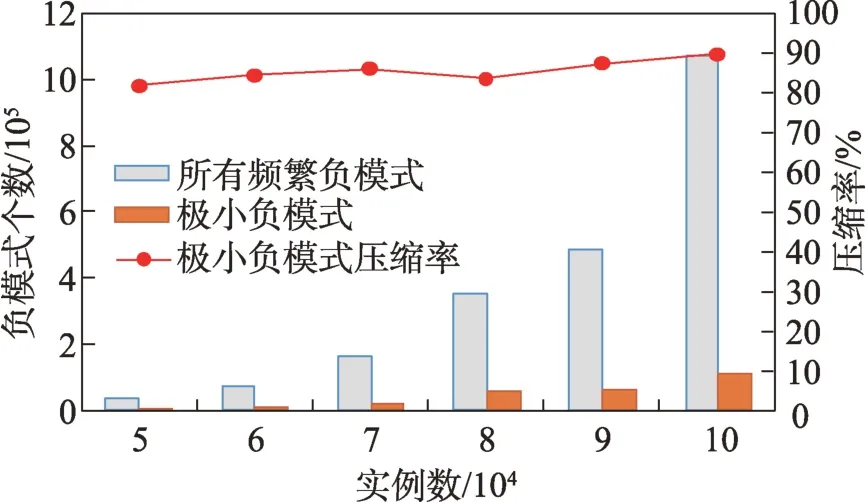
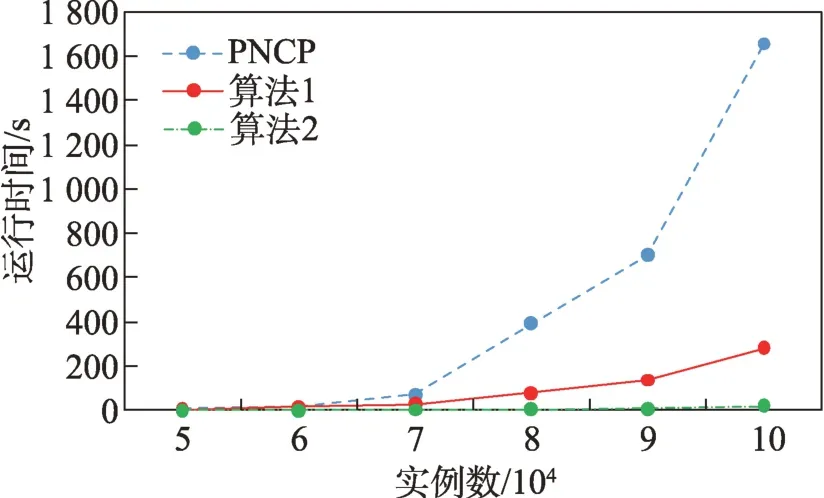
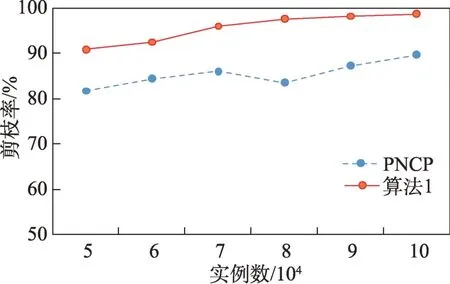
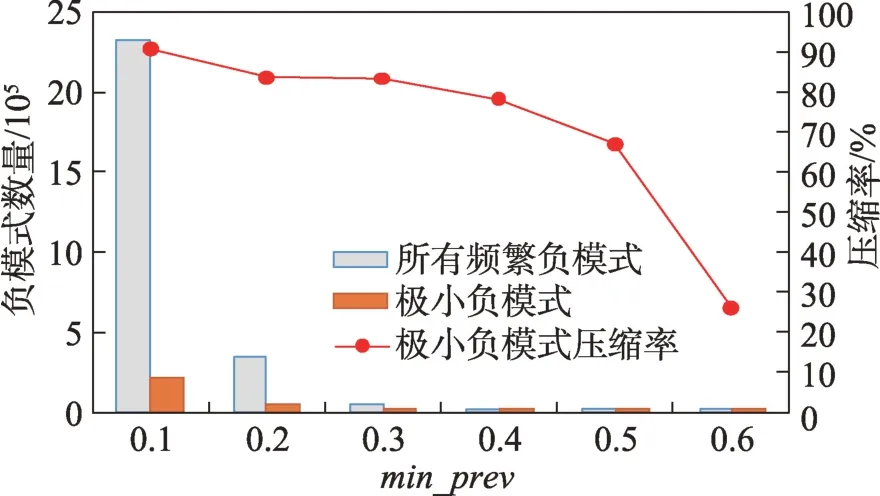
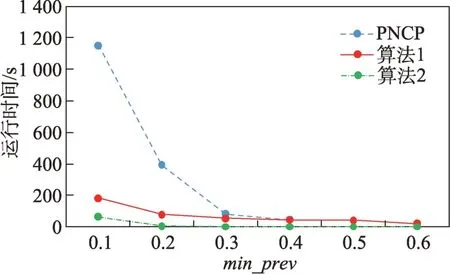
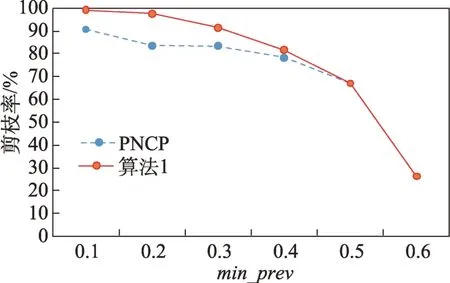
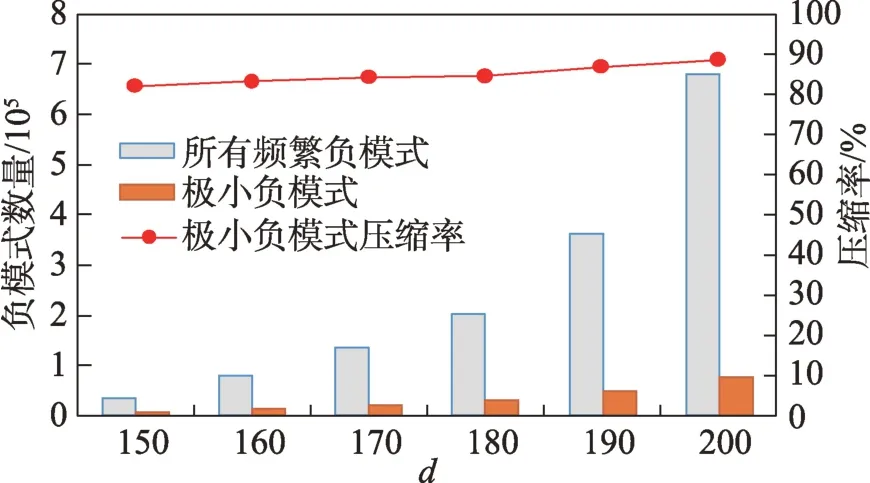
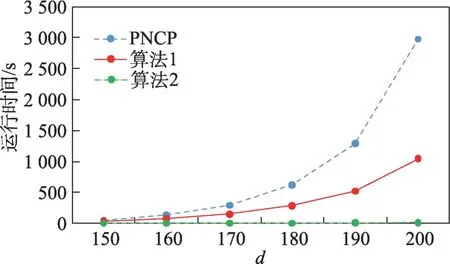
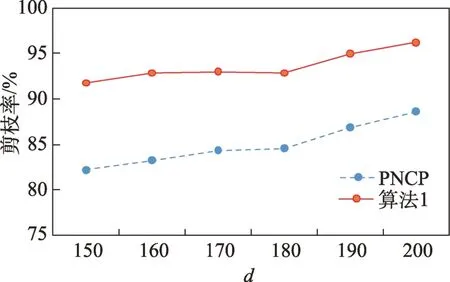
定义2(候选负co-location模式)一个负co-location模式T=X⋃,如果满足PI(X)≥min_prev,PI(Y)≥min_prev,且PI({X⋃Y}) 含有k个正项特征的候选负co-location 模式T=X⋃的参与度nPI(T)的计算公式表示如下[17]: 其中,PR({X⋃Y},xi)是特征xi(xi∈X)在模式X⋃Y中的参与率。负co-location 模式的参与度与其正项特征的参与率有着密切的关系。 定义3(频繁负co-location 模式)[17]给定一个候选负co-location 模式T=X⋃,且用户给定最小参与度阈值为min_prev,若满足nPI(T)≥min_prev,则称候选负co-location 模式T=X⋃为频繁负co-location模式。 在文献[17]的定义中,从非频繁的模式中挖掘出负co-location 模式X⋃,其要求X和Y都是频繁的。此条件可极大地减少无趣的负模式产生,使挖掘出的结果更有意义。将模式X与模式Y不同时出现的概率定义为负模式X⋃的参与度,合理地反映出了模式X与模式Y之间的负相关性。 例3如图1 所示,若设置min_prev=0.5,模式{A}和模式{C}是频繁的正co-location 模式,且PI({A,C})=0.25 基于正co-location 模式参与率的反单调性及负co-location 模式参与度的定义,在负co-location 模式挖掘中,找出具有可推导出所有频繁负co-location 模式的紧凑表示,同时高效地挖掘出所有频繁负colocation 模式是有意义的。 引理2给定一个空间候选负co-location 模式T=X⋃,若存在X=X1⋃X2,且X1⋃和X2⋃是频繁的负co-location 模式,那么候选负co-location 模式T=X⋃也是频繁的。 证明给定两个频繁负co-location 模式X1⋃和X2⋃,一个候选负co-location 模式T=X⋃,且X=X1⋃X2,对于任意的ai∈X1,bi∈X2,根据引理1,可得到: 引理得证。 引理3给定一个频繁负co-location模式T=X⋃,若存在Y⊂Y′且Y′是频繁的正co-location 模式,那么负co-location 模式T′=X⋃也是频繁的。 证明给定一个频繁负co-location模式T=X⋃,存在Y⊂Y′且PI(Y′)≥min_prev,对于任意的ai∈X,根据引理1,都有: PR({X⋃Y},ai})≥PR({X⋃Y′},ai) 根据负模式的参与度定义,有: min(1-PR({X⋃Y′},ai))≥min(1-PR({X⋃Y},ai})) 即: nPI(X⋃=min(1-PR({X⋃Y′},ai))≥min_prev 引理得证。 引理4给定含k个正项特征的候选负co-location模式T=X⋃,若频繁正co-location 模式X的最大参与率满足max(PR({X},x1),PR({X},x2),…,PR({X},xk))≤1-min_prev(xi∈X),则候选负co-location 模式T=X⋃是频繁的。 证明给定含有k个正项特征的候选负co-location模式T=X⋃,若满足: max{PR({X},x1),PR({X},x2),…,PR({X},xk)}≤1-min_prev 根据引理1 可得: 引理得证。 由引理2 和引理3,看到了负co-location 模式具有一种“向上包含”性质,该性质类似频繁项集挖掘中的“向下闭合”性质。为此,本文提出了极小负colocation 模式新概念。 定义4(极小负co-location 模式)给定一个频繁负co-location 模式T=X⋃,存在X′⋃X″=X,Y′⊂Y,且X′、X″和Y′均为频繁的正co-location 模式。若负co-location 模式X′⋃和X″⋃不同时为频繁负colocation 模式,且X⋃也不是频繁负co-location 模式,则称模式T=X⋃为极小负co-location 模式。 引理5通过极小负co-location 模式可推导出所有频繁负co-location 模式。 证明给定一个非极小负co-location 模式的频繁负co-location 模式T=X⋃。若该模式不能由极小负co-location 模式推导得到,则该模式需同时满足如下条件: (1)对于模式Y的任一子集Y′,负co-location 模式X⋃′均不是频繁co-location 模式; (2)对于X=X′⋃X″,模式X′⋃和X″⋃不能同时为频繁负co-location 模式。 由定义4 可知,满足上述两个条件的频繁负colocation 模式为极小负co-location 模式,与给定条件冲突,故极小负co-location 模式可推导出所有频繁负co-location 模式。 引理得证。 例4如图1 所示的实例分布中,给定最小支持度阈值min_prev=0.5,极小负co-location 模式及被其“向上包含”的频繁负co-location 模式如表1 所示。 由表1 可知,在这个例子中,频繁负co-location模式共有20 个,而极小负co-location 模式仅为10 个。 Table 1 Minimal negative patterns and their contained negative patterns表1 极小负模式及其包含的负模式 本章给出了极小负co-location模式挖掘算法和基于极小负co-location 模式推导出所有频繁负colocation模式的算法,具体步骤分别见算法1和算法2。 算法1挖掘极小负co-location 模式 算法2基于极小负co-location 模式推导所有频繁负co-location 模式 极小负co-location 模式挖掘算法包含如下五步: (1)计算所有实例的邻居关系NT,使用任一已有算法挖掘频繁正co-location 模式,并存储每个模式的最大参与率。 (2)由低阶模式到高阶模式,将频繁正co-location模式通过两两组合的方式产生候选负co-location模式。 (3)使用引理2、引理3 及引理4 对该候选模式进行剪枝,并识别候选模式是否为极小负co-location模式。 (4)若该候选模式未被剪枝,则扫描实例的邻居关系NT确定其表实例。 (5)通过表实例计算出该候选负co-location 模式的参与度,若该模式参与度大于用户给定参与度阈值,则其为极小负co-location 模式。 具体过程见算法1。 算法1 中,首先扫描一次空间实例分布数据,计算每个实例的邻居,构成邻居关系集合NT。 基于邻居关系集合NT,通过任一已有算法挖掘出所有频繁正co-location 模式,同时保存所有频繁正co-location 模式的最大参与率。 将所有频繁正co-location 模式按字典序排序,字典序保证了在计算高阶模式时,该模式的低阶子集已被计算。通过频繁正co-location 模式两两组合的方式形成候选负co-location 模式。根据候选负colocation 模式的定义,当频繁正co-location 模式数量增加时,候选负co-location 模式数量也随之增加。 若候选负co-location 模式未被剪枝,则对邻居关系集合进行扫描,确定该模式的表实例,通过表实例计算出该模式的参与度nPI,并判断该模式是否为极小负co-location 模式。 本算法的时间复杂度与候选模式数相关,而候选模式数与距离阈值、参与度阈值、特征数、实例数等相关,下面的分析从假设正频繁模式数开始。假设频繁正co-location 模式个数为k,则循环次数为,则可生成个候选负co-location 模式,该过程的时间复杂度为O(k2)。 若候选负co-location 模式未被剪枝,则需通过扫描邻居关系NT确定该模式表实例,并通过表实例计算该模式的参与度nPI,从而确定其是否为极小负co-location 模式。假设有m个候选负co-location模式未被剪枝,且其平均长度为Navg,则确定m个候选负co-location 模式表实例的时间复杂度为m×Tfilter_clique_inst(Navg),其中Tfilter_clique_inst(Navg)为确定一个Navg阶模式的表实例所用时间,这也是算法最耗时的部分,剪枝引理的意义就在于通过提前剪枝减少表实例的计算。 引理5 证明了基于挖掘到的极小负co-location模式可以推导出所有频繁负co-location 模式,算法2给出了推导过程。 算法2 中,通过将频繁正co-location 模式两两组合生成候选负co-location 模式,若候选负co-location模式满足引理2 或引理3,则该模式为频繁负colocation 模式,并将该模式加入集合中。 在算法2 的过程2 及2.1 中,假设频繁正colocation 模式个数为k,则循环次数为则可生成个候选负co-location 模式,该过程的时间复杂度为O(k2) 。算法2 的过程2.1.1 及2.1.2 为查询及判断,在算法的存储结构中使用了哈希表的形式,故该过程的时间复杂度为O(1)。 在给定的空间数据集中,参与度阈值min_prev一定时,距离阈值d越大,邻居关系NT越多,挖掘到的频繁正co-location 模式越多,阶数越大,产生的频繁负co-location 模式也越多。距离阈值d一定时,参与度阈值min_prev越小,挖掘到的频繁正co-location模式越多,阶数越大,扫描邻居关系集合NT的次数越多,算法的运行时间越长,产生的频繁负colocation 模式也越多。 现有的PNCP 算法中[17],假设频繁正co-location模式个数为k,通过两两组合产生候选负co-location模式的方式,可组合产生个候选负co-location模式,其时间复杂度为O(k2)。假设有l个候选负co-location模式未被剪枝,且其平均长度为Navg,则确定l个候选负co-location模式表实例的时间复杂度为l×Tfilter_clique_inst(Navg),其中Tfilter_clique_inst(Navg)为确定一个Navg阶模式的表实例所用时间。在负colocation 模式挖掘中,查找模式的表实例为最耗时的部分且频繁的负co-location 模式数量巨大,本文在剪枝效率上有较大提升,算法1 的时间复杂度中未被剪枝的候选模式数m≪l,故本文算法效率优于现有PNCP 算法。 算法1 基于引理2 及引理3,通过判断候选模式是否满足这两个引理,只有都不满足且该候选模式的参与度大于参与度阈值时,该候选模式才为极小负co-location 模式;同样,算法2 基于极小负colocation 模式,若候选模式满足引理2 或引理3,则该模式为频繁的负co-location 模式。引理5 基于引理2及引理3 证明了极小负co-location 模式推导所有频繁负co-location 模式的完备性。 目前,仅有文献[17]的工作是挖掘频繁负colocation 模式的,为评估本文提出的极小负co-location模式的压缩率和基于极小负co-location 模式挖掘所有频繁负co-location 模式方法的有效性,在真实和合成数据集上将本文中提出的算法1 及算法2 和文献[17]中的PNCP 算法进行了比较(https://github.com/GuangyaoWang/e-NCP)。由引理5 及实验证实,算法2 中,由极小负co-location 模式推导出的频繁负colocation 模式与PNCP 算法挖掘得到的频繁负colocation 模式数量一致。所有算法都采用Java 编写,实验环境为Win10 系统,Core i7 CPU 和16 GB 内存的计算机。 在实验中选取的真实数据集为云南贡山某区域的植被分布数据,数据分布图如图2 所示,该数据集包含箭竹、冷杉、桤木、铁杉、云南松等25 个树种,共有13 349 个植株实例。考虑参与度阈值和距离阈值的变化,比较极小负co-location 模式的压缩率、算法1与PNCP 算法的剪枝率和3 个算法的运行效率。 Fig.2 A vegetation distribution data set图2 一个植被分布数据集 4.1.1 参与度阈值的变化 在本小节实验中,均固定距离阈值d=1 500 m,设置参与度阈值由0.1 到0.6 进行实验。 随着参与度阈值的变化,算法1 挖掘出的极小负co-location 模式数量、算法2 推导出的频繁负colocation 模式数量及PNCP 算法挖掘得到的频繁负co-location 模式数量如图3 中的柱状图所示,极小负co-location 模式的压缩率如图3 中的折线图所示。当参与度阈值增大时,频繁负co-location 模式数量有较大的减少趋势,而极小负co-location 模式数量一直较少,并有较小的减少趋势。由于频繁负co-location 模式数量的减少,极小负co-location 模式“向上包含”的模式数量也随之减少,进而压缩率减少。不过,当参与度阈值为0.1 时,极小负co-location 模式数量的压缩率高达80%。 Fig.3 Effect of min_prev on the number of negative patterns in real data图3 真实数据中参与度阈值对负模式数量的影响 算法1、算法2 与PNCP 算法随着参与度阈值的变化,挖掘耗时如图4 所示,算法1 的运行效率优于PNCP 算法,算法2 的运行耗时非常小。说明挖掘极小负co-location 模式,得到精简的、用户更易理解和使用的极小集合,再由极小负co-location 模式推导出所有频繁负co-location 模式,其效率仍优于直接挖掘所有频繁负co-location 模式的效率。从图4 可以看到,当参与度阈值为0.1 时,算法1 的效率是PNCP 算法的4 倍。 Fig.4 Effect of min_prev on running time in real data图4 真实数据中参与度阈值对运行时间的影响 算法1 与PNCP 算法随着参与度阈值的变化,剪枝率如图5 所示,随着参与度阈值的增大,剪枝率出现了明显的下降趋势,当参与度阈值小于等于0.5时,算法1 的剪枝率均高于PNCP 算法,当参与度阈值大于0.5 时,由于在该阈值下引理4 的剪枝失效,两种算法的剪枝率相同,该问题在本小节的讨论中进行了详细分析。特别地,当参与度阈值等于0.1 时,算法1 的剪枝率达到85%。 Fig.5 Effect of min_prev on pruning ratio in real data图5 真实数据中参与度阈值对剪枝率的影响 4.1.2 距离阈值的变化 在本小节实验中,均固定参与度阈值min_prev=0.1,设置距离阈值d由1 300 m 到1 800 m 进行实验。 随着距离阈值的变化,算法1 挖掘出的极小负co-location 模式数量、算法2 推导出的频繁负colocation 模式数量及PNCP 算法挖掘得到的频繁负co-location 模式数量如图6 中的柱状图所示,极小负co-location 模式的压缩率如图6 中的折线图所示。由柱状图可看出,随着距离阈值的增大,导致了邻居关系的增加,进而使频繁负co-location 模式数量逐渐增加,而极小负co-location 模式数量没有明显的增加,频繁负co-location 模式的增加使得极小负co-location模式压缩率也随着增加。从实验发现,极小负colocation 模式的压缩率均保持在80%以上。 Fig.6 Effect of d on the number of negative patterns in real data图6 真实数据中距离阈值对负模式数量的影响 算法1、算法2 和PNCP 算法随着距离阈值变化,挖掘耗时的变化如图7 所示。PNCP 算法随着距离阈值的增加,挖掘时间有较大幅度的上升趋势,而算法1 则较为平缓,算法2 的运行耗时均处于极低的状态,算法1 的运行时间均优于PNCP 算法。而当距离阈值取1 800 m 时,PNCP 算法的运行时间是算法1 的4 倍。 Fig.7 Effect of d on running time in real data图7 真实数据中距离阈值对运行时间的影响 算法1 和PNCP 算法随着距离阈值的变化,剪枝率如图8 所示,随着距离阈值增大,剪枝效率越来越高,算法1 的剪枝率明显优于PNCP 算法,且算法1 的剪枝率均高于80%。 Fig.8 Effect of d on pruning ratio in real data图8 真实数据中距离阈值对剪枝率的影响 在合成数据集上的实验,使用的数据为6 个特征数为26,实例分布范围为(20 000×20 000)的合成数据集,每个特征的实例数随机产生,总实例数由50 000 到100 000。考虑实例数、参与度阈值及距离阈值的变化,分别对比极小负co-location 模式的压缩率、3 个算法的运行耗时和算法1 与PNCP 算法的剪枝率。 4.2.1 实例数的变化 在本小节实验中,均固定距离阈值d=170,参与度阈值min_prev=0.2,实例数由50 000 到100 000,在6 个合成数据集下进行实验。 随着实例数的变化,算法1 挖掘出的极小负colocation 模式数量、算法2 推导出的频繁负co-location模式数量及PNCP 算法挖掘得到的频繁负co-location模式数量如图9 中的柱状图所示,极小负co-location模式压缩率如图9 中的折线图所示。随着实例数的增加,实例的分布密度逐渐增大,在同样的距离阈值下产生的邻居关系增多,使得挖掘的频繁正colocation 模式数量增加,进而使得负co-location 模式数量也随之增加。频繁负co-location 模式数量有较大的增幅,而极小负co-location 模式数量较少且增幅较小,压缩率基本维持在90%左右。 Fig.9 Effect of number of instances on the number of negative patterns in synthetic data图9 合成数据中实例数对负模式数量的影响 算法1、算法2 和PNCP 算法随着实例数的变化,挖掘耗时如图10 所示。当实例数增大时,PNCP 算法的频繁负co-location 模式挖掘时间呈现较大幅度的上升,而算法1 挖掘极小负co-location 模式的耗时上升趋势较缓,算法2 的耗时极低,呈现小幅度上升趋势。当实例数达到100 000 时,算法1 的运行时间仅为PNCP 算法运行时间的17%。 Fig.10 Effect of number of instances on running time in synthetic data图10 合成数据中实例数对运行时间的影响 随着实例数的增加,算法1 与PNCP 算法的剪枝率如图11 所示。随着实例数的增大,PNCP 算法和算法1 的剪枝率均呈现上升趋势,由于合成数据为随机生成,实例的位置分布不同,根据剪枝策略的条件,满足剪枝条件的模式数量可能存在差异,故在实例数为80 000 的数据中,PNCP 算法的剪枝率有所下降。 4.2.2 参与度阈值的变化 本小节实验在特征数为26,实例总数为80 000的合成数据集下进行实验。均固定距离阈值d=170,设置参与度阈值由0.1 到0.6 进行实验。 Fig.11 Effect of number of instances on pruning ratio in synthetic data图11 合成数据中实例数对剪枝率的影响 随着参与度阈值的变化,算法1 挖掘出的极小负co-location 模式数量、算法2 推导出的频繁负colocation 模式数量及PNCP 算法挖掘得到的频繁负co-location 模式数量如图12 中的柱状图所示,极小负co-location 模式压缩率如图12 中的折线图所示。当参与度阈值增大时,挖掘到的频繁负co-location 模式数量明显减少,极小负co-location 模式也逐渐减少,“向上包含”的模式数量逐渐减少,进而使得极小负co-location 模式的压缩率由91%逐渐减小为26%。 Fig.12 Effect of min_prev on the number of negative patterns in synthetic data图12 合成数据中参与度阈值对负模式数量的影响 算法1、算法2 和PNCP 算法随着参与度阈值变化,挖掘耗时如图13 所示。3 个算法的运行时间均随着参与度阈值的增大呈现下降趋势。当参与度阈值较低时,PNCP 算法的挖掘耗时长,算法1 耗时明显优于PNCP 算法,当参与度阈值较高时,由于引理4的剪枝失效,算法1 与PNCP 算法的挖掘的耗时相同。算法2 的挖掘耗时均处于较低水平。比起PNCP 算法,算法1 将耗时都调整到较低的水平,当参与度阈值为0.1时,算法1的运行时间较PNCP算法提高了84%。 Fig.13 Effect of min_prev on running time in synthetic data图13 合成数据中参与度阈值对运行时间的影响 随着参与度阈值的变化,PNCP 算法与算法1 的剪枝率如图14 所示。随着参与度阈值增大,挖掘出的频繁负co-location 模式数量逐渐减少,故剪枝率也呈现下降趋势,当参与度阈值为0.1 时,算法1 的剪枝率高达99%。 Fig.14 Effect of min_prev on pruning ratio in synthetic data图14 合成数据中参与度阈值对剪枝率的影响 4.2.3 距离阈值的变化 本小节在特征数为26,实例数为90 000 的合成数据集下进行实验。均固定参与度阈值min_prev=0.3,设置距离阈值由150 到200 进行实验。 随着距离阈值的变化,算法1 挖掘出的极小负co-location 模式数量、算法2 推导出的频繁负colocation 模式数量及PNCP 算法挖掘得到的频繁负co-location 模式数量如图15 中的柱状图所示,极小负co-location 模式压缩率如图15 中的折线图所示。随着距离阈值的增大,频繁负co-location 模式数量有大幅的增长,而极小负co-location 模式数量增长较缓慢且压缩率较高并有小幅的增长,极小负co-location 模式的压缩率均高于80%。 Fig.15 Effect of d on the number of negative patterns in synthetic data图15 合成数据中距离阈值对负模式数量的影响 算法1、算法2 和PNCP 算法随着距离阈值变化,挖掘耗时如图16 所示。当距离阈值增大时,PNCP 算法呈现较快的上升趋势,算法1 呈现较缓的上升趋势,而算法2 的耗时均维持在极低的水平。 Fig.16 Effect of d on running time in synthetic data图16 合成数据中距离阈值对运行时间的影响 随着距离阈值的变化,PNCP 算法与算法1 的剪枝率如图17 所示,随着距离阈值的增大,两个算法的剪枝率均呈现上升趋势,算法1 的剪枝率均高于PNCP 算法。 Fig.17 Effect of d on pruning ratio in synthetic data图17 合成数据中距离阈值对剪枝率的影响 本文在真实及合成数据集上进行了大量实验,实验均表明本文算法优于现有的PNCP 算法。本文在挖掘极小负co-location模式的基础上推导出所有频繁负co-location模式,推导过程耗时极低,使用本文算法挖掘出所有频繁负co-location模式仍是高效的。 近年许多学者提出了高效的正co-location 模式的挖掘方法,由于本文旨在提高负co-location 模式挖掘效率,且使用不同的正co-location 模式挖掘算法的运行时间不尽相同,故本文实验的运行时间仅为挖掘负co-location 模式的时间。 讨论:在参与度阈值变化的实验中,当参与度阈值大于等于0.5 时,算法1 与PNCP 算法的运行时间及剪枝率相同。当参与度阈值等于0.5时,由引理4可得: 给定一个候选负co-location 模式T=X⋃,频繁正co-location 模式X的最大参与率满足max(PR({X},x1),PR({X},x2),…,PR({X},xk))≥0.5。使用引理4 的剪枝条件为max(PR({X},x1),PR({X},x2),…,PR({X},xk))≤0.5。根据以上条件,只有当频繁正co-location 模式X中所有特征的参与率均为0.5 时,该剪枝才能生效,而这类模式在挖掘过程中是极其罕见的,因此与PNCP 算法相比,运行效率并未提高。同理可得,当参与度阈值大于0.5 时,该剪枝条件无法生效,故PNCP 算法与算法1 的运行时间相同。 在负co-location 模式挖掘中,随着参与度阈值的增大,挖掘出的模式数量呈现极大程度的下降,从实验的运行时间也可看出,在参与度阈值较低时时间耗费是巨大的。当参与度阈值小于0.5时,负co-location模式的挖掘结果数量非常巨大,剪枝策略运用到这类情况下具有重要的意义。 由于负co-location 模式自身的特点,现有的负关联规则、负序列等挖掘算法难以直接运用到负colocation 模式挖掘中来。本文提出极小负co-location模式新概念,研究了极小负模式与频繁负模式的关系、负模式挖掘的有效剪枝策略等,从而设计了有效的算法来挖掘极小负co-location 模式,进而由极小负colocation 模式推导出所有频繁负co-location 模式。在真实和合成数据集上进行了广泛的实验,与现有负colocation模式挖掘算法在效果及效率上进行了比较,验证了其正确性及高效性。在未来工作中将会考虑基于模糊集论方法研究负co-location 模式的挖掘等。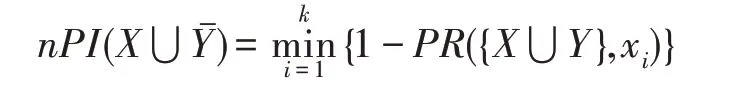


3 相关算法



4 实验与分析
4.1 真实数据集上的实验与分析


4.2 合成数据集上的实验与分析
5 结束语

