带有局部坐标约束的半监督概念分解算法

李会荣，张 林，赵鹏军，李 超

商洛学院数学与计算机应用学院，陕西商洛 726000

在机器学习、模式识别等具体应用中，人们通常会遇到高维数据，如何提取这些高维数据的潜在结构信息，将是机器学习领域的一大挑战。非负矩阵分解（non-negative matrix factorization，NMF）是处理高维数据最流行的技术之一，它将原始的数据矩阵分解为两个或两个以上低阶矩阵的乘积[1-2]，目前已经成功应用到特征提取[3]、数据挖掘[4-5]、图像表示[6]等领域中。然而，NMF只能应用于非负的数据矩阵，同时也不能核化[7]。为了克服这些缺点，Xu等人提出了一种用于文档聚类的CF（concept factorization）算法，它将每一个基向量（或概念）都表示为数据点的线性组合，每一个数据点表示为基向量的线性组合[7]。与NMF 相比，CF 不仅可以核化，而且还可以应用到非负数据的情况，但是它并没有考虑到数据的流形结构或者稀疏性等特征。为此，研究者针对CF提出了多种改进的算法。例如：Cai等人将图正则化融入到CF 中提出了一种局部一致的概念分解（locally consistent concept factorization，LCCF）算法[8]，有效提取了数据的局部几何结构信息。Liu 等人提出了一种局部坐标的概念分解（local coordinate concept factorization，LCF）算法[9]，利用局部坐标约束学习了数据的稀疏性。Li等人利用局部坐标和图正则化提出了一种带有局部坐标的图正则化的概念分解（graphregularized CF with local coordinate，LGCF）算法[10],它不仅使得学习的系数更稀疏，而且有效维持了数据空间的几何结构。

然而前面提到的算法都是无监督的学习方法，它们不能利用数据有效的标签信息。研究者发现，当利用少量的标签数据结合大量的无标签数据，能够大大提高机器学习算法的性能[11-16]。近年来也提出一些将数据的部分标签信息加入到CF算法中的半监督学习方法。例如：Liu等人将标签约束加入到CF算法中，提出了约束概念分解（constrained concept factorization，CCF）算法[17]，CCF可以保证拥有同类标签的数据在低维表示空间中拥有相同的概念；Li等人同时考虑数据的标签信息和局部流形正则化，提出了一种半监督图正则化识别的概念分解（graph-based discriminative concept factorization，GDCF）算法[18]，它可以将同类的数据点在新的表示空间中尽可能地接近或者位于同一轴线上，提高了GDCF算法的识别能力。

考虑到有限的标签信息和局部坐标约束，提出了一种带有局部坐标约束的半监督的概念分解（semisupervised CF with local coordinate constraint，SLCF）算法。SLCF 利用局部坐标约束使得学习的系数更稀疏，利用标签信息增强了数据不同类之间的识别能力。利用辅助函数证明了SLCF算法的收敛性，并在多个数据集上进行实验，表明SLCF算法具有比较好的聚类性能。

1 基本NMF和CF算法

给定一个非负的数据矩阵X=[x1,x2,…,xn]∈Rm×n，其中每个数据点xi为一个m维的向量。基本的NMF算法就是寻找两个非负低秩数据矩阵U∈Rm×k，V∈Rn×k，使得X≈UVT，其中k≤min{m,n}。通常，利用欧式距离来衡量这种近似程度，因此NMF 算法可以转化为求解如下的优化问题[1-2]：

其中，U称为基矩阵，V称为系数矩阵。

在CF算法中，将NMF算法中的基向量uj（基矩阵U的第j列）表示为每个数据点xi的线性组合，即，其中wij≥0,令W=[wij]∈Rn×k，则CF 算法将数据矩阵X分解为如下形式：

利用欧氏距离来度量这种近似程度，因此CF 算法求解如下的优化问题：

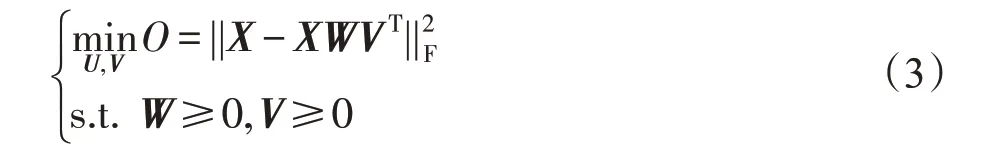
由于目标函数对于W或者V是凸的，但是同时对W和V是非凸的，因此很难求解优化问题（3）的全局最优解。Xu等人提出了利用乘性迭代方法得到优化问题（3）局部最优解如下[7]：

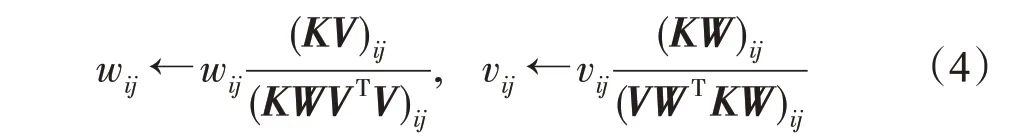
其中，K=XXT。

2 带有局部坐标的半监督概念分解（SLCF）算法

由于CF 算法不能利用有限的标签信息，为一个无监督的学习方法，同时也不能保证学习系数矩阵具有稀疏性。为了更好利用数据的有限的标签信息和稀疏性，提出了一种带有局部坐标约束的半监督的概念分解（SLCF）算法。

2.1 标签约束矩阵

为了利用有效的标签信息，Liu等人利用标签约束矩阵A，提出了一种约束的概念分解算法[17]。假设数据集X有c类，前l个数据点x1,x2,…,xl是有标签的，且属于c类中的某一类，余下的n-l个数据点xl+1,xl+2,…,xn是未知标签的，指示矩阵B∈Rl×c定义如下：

结合无标签的数据点，定义标签约束矩阵A∈Rn×(c+n-l)如下[15]：

其中，In-l为(n-l)×(n-l)的单位矩阵。标签约束矩阵A能够保证同类标签的数据点映射到低维表示空间中拥有相同的标签。引入辅助矩阵Z，使得V=AZ，就可以将CF算法推广到半监督的学习方法，即数据矩阵X可以表示为：

2.2 局部坐标约束

为了学习稀疏系数，刘海峰等人引入局部坐标约束，提出了一种局部坐标的概念分解（local-coordinate CF，LCF）算法[9]。首先，引入坐标编码的定义[19]：

定义1一个坐标编码就是一对(γ,C)，其中C∈RD是一个锚点集，γ是一个锚点x∈RD到[γv(x)]v∈C∈R|C|的映射，并且满足于是，在RD中的x有γ(x)=∑v∈Cγv(x)v。

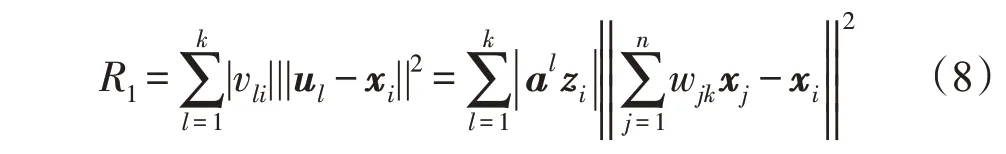
其中，ak表示标签约束矩阵A的第k行，zi表示辅助矩阵Z的第i列。

2.3 提出的SLCF算法

标签信息可以提高CF 算法的聚类性能，局部坐标约束R1可以使CF学习的系数矩阵更稀疏，因此将有限的标签信息和局部坐标约束R1融入到CF 算法中，提出了一种半监督的带有局部坐标的概念分解（SLCF）算法，即求解如下优化问题：

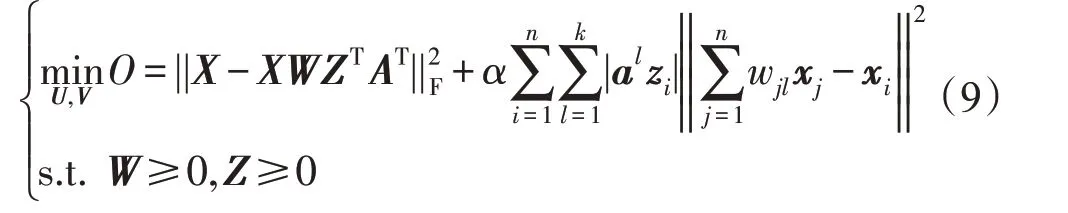
其中，α>0 为平衡参数，主要衡量局部坐标约束项的影响程度。

很显然，SLCF算法的目标函数关于变量W和V是非凸的，很难求它的全局最优解。可以利用乘子更新规则[20]迭代优化问题（9），可以得到SLCF算法的迭代更新规则。

首先，将优化问题式（9）的目标函数可以表示为：

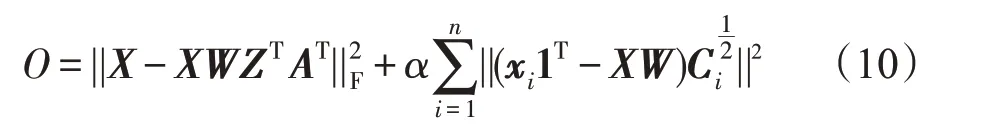
其中，Ci=diag(|aiz1|,|aiz2|,…,|aizk|)∈Rk×k，diag(v)表示由向量v构成的对角矩阵，1 表示元素全为1 的k×1的向量。利用矩阵的性质，可以得到：

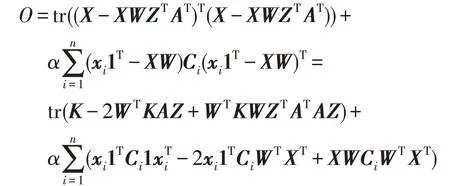
其中，K=XTX。假设φik、ψjk分别为wik≥0,zjk≥0的拉格朗日乘子，令Φ=[φik]，Ψ=[ψjk]，则优化问题（9）的拉格朗日函数L为：

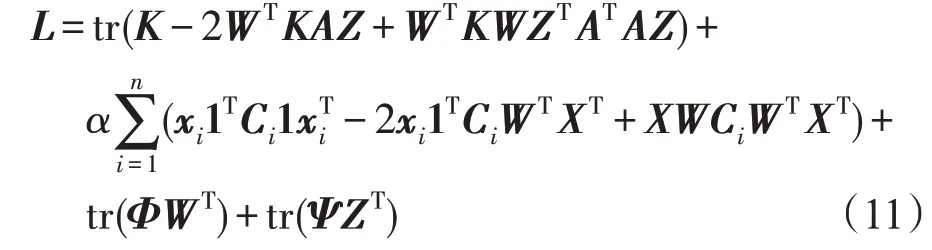
令e=diag(K)∈Rn，f=diag(WTKW)∈Rk，定义E=(e,e,…,e)∈Rn×k，F=(f,f,…,f)T∈Rn×k，则拉格朗日函数L关于矩阵变量W和Z的偏导数分别为：

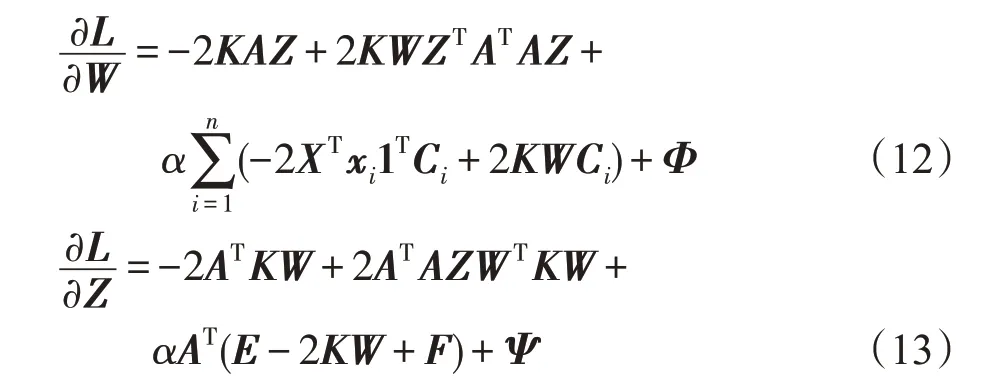
利用Kuhn-Tucher条件φikwik=0，ψjkzjk=0，有：

从优化问题（9）中可以看出，当α=0 时，SLCF算法就为CCF算法。

2.4 计算复杂度分析

为了精确分析SLCF 算法的复杂度，计算SLCF算法更新规则每次迭代过程中加法、乘法、除法运算的个数，并与CF和NMF进行比较，结果如表1所示，其中n表示数据点的个数，m表示数据的维数，k表示特征因子的维数，k≤min{m,n}。

对于局部坐标约束，与CF算法相比，每次迭代中SLCF 算法比CF 算法多2n2k+2nk2次加法与乘法运算。对于SLCF算法，由于约束标签矩阵A的每行只有一个非零元素1，因此在计算矩阵AZ时不需要额外的加法与乘法运算，但在计算ATB（B∈Rn×k）时只需nk次加法运算。在CF、SLCF算法中，计算核矩阵K需要n2m次加法与乘法运算。因此由表1 可以看出，每次迭代过程中SLCF、CF 算法总的计算复杂度都为O(n2k+n2m)。

3 SLCF算法收敛性证明

关于SLCF 算法的迭代更新规则（14）、（15），下面定理从理论上保证了SLCF算法的收敛性。

定理1优化问题（9）的目标函数O在迭代更新规则（14）、（15）下是非增的。目标函数O在迭代更新规则（14）、（15）下是不变的当且仅当W和Z是一个稳定点。

为了证明收敛性定理，给出以下引理：

引理1如果存在F(x)的辅助函数G(x,x′)满足G(x,x′)≥F(x)，且G(x,x)=F(x)，则F(x)在以下更新规则下是非增的[21]：

证明

现在，证明关于变量W的迭代更新规则式（14）正是某一合适的辅助函数在更新规则（16）下可得。令矩阵W中任意元素用wab表示，Fab表示式（9）中的目标函数O仅与wab有关。目标函数O关于变量wab的一阶、二阶导数分别为：

Table 1 Computational operation counts for each iteration in NMF,CF and SLCF表1 在NMF、CF、SLCF中每次迭代运算的个数

令Hab表示式（9）中的目标函数O仅与zab有关，计算目标函数O关于变量zab的一阶、二阶导数分别为：

由于式（19）、式（26）分别为Fab、Hab的辅助函数，因此Fab、Hab在更新规则式（14）、式（15）下是非增的。因此优化问题式（9）中的目标函数O在迭代更新规则（14）、（15）下是非增的。定理1得证。

4 数值实验

为了验证SLCF算法的有效性，将在COIL20、YaleB、MNIST数据库上进行实验，并与K-means、NMF[2]、CF[8]、局部坐标的概念分解（LCF）[9]、约束概念分解算法（CCF）[15]以及非负局部坐标分解算法（non-negative local coordinate fact-orization，NLCF）[22]进行比较。

从每个数据库中随机选择P（P从2到10）类样本，同时在这P类样本构成的数据子集X上进行实验。设置新表示空间的维数等于数据类别的个数P，并利用K-means 算法对系数表示矩阵V进行聚类，在每次实验中K-means 重复20 次并记录最好结果。在半监督学习算法CCF、SLCF 中，从每类样本中随机选择20%样本作为已知的标签信息，并用它构造标签约束矩阵A。在NMF、CF、NLCF、LCF、CCF、SLCF 中，最大迭代次数T=200，参数α将在后面讨论，对于每一个给定的聚类数P，每个实验独立运行20次并计算平均聚类结果。采用聚类精度（accuracy，AC）和归一化互信息（normalized mutual information，NMI）来评价聚类性能[22-23]。

4.1 在COIL20数据集上的实验

COIL20图像数据集包含20类共1 440张灰色图像，每张图像裁剪成32×32 像素，表示为1 024维的向量。在COIL20数据库上实验结果如表2、表3所示。

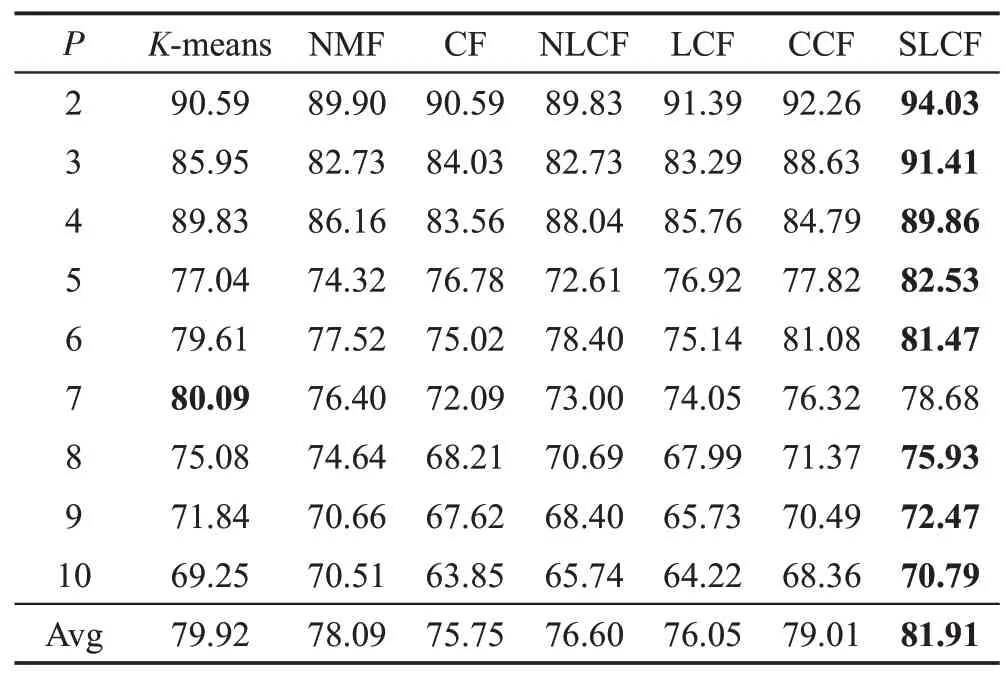
Table 2 Clustering AC performance on COIL20 database表2 在COIL20数据集的AC聚类性能%

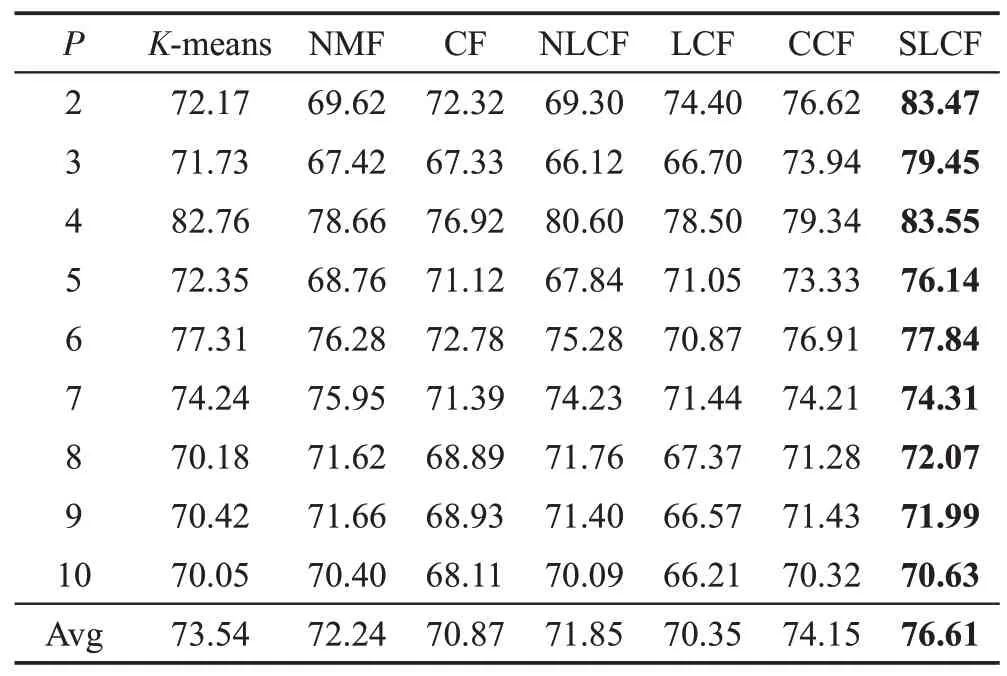
Table 3 Clustering NMI performance on COIL20 database表3 在COIL20数据集的NMI聚类性能%

从表2、表3 中可以看出，不论从平均聚类精度，还是从平均的归一化互信息来看，提出的SLCF算法的性能优于其他比较的方法。与CF 和LCF 算法相比，SLCF 在平均聚类精度AC 上分别提高了6.16 个百分点、5.86个百分点，在NMI上分别提高了5.74个百分点、6.26个百分点。因此SLCF算法的平均聚类性能优于CF、LCF 方法，主要由于SLCF 算法考虑了数据有效的标签信息和局部坐标约束，进一步提高了算法的聚类性能。

4.2 在YaleB数据集上的实验

Yale B包含有38个人在不同灯光变化下获取的2 414 张人脸图像，每个人大约有59～64 张图像。在本实验中，每类随机选择50张图像进行实验，并且每张图像裁剪成像素，实验结果如表4、表5所示。

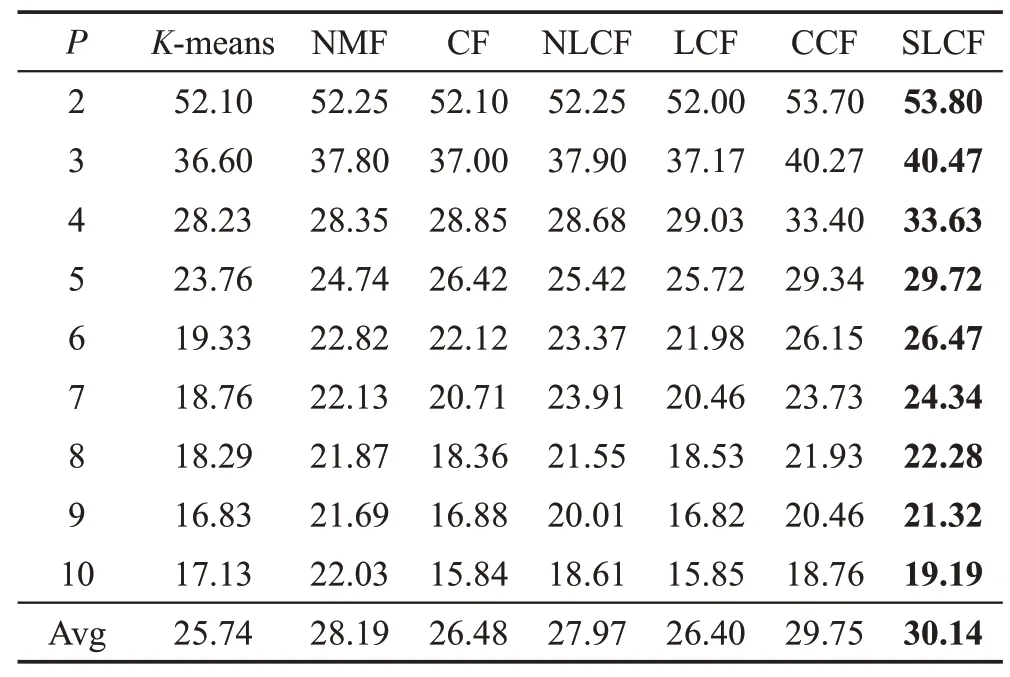
Table 4 Clustering AC performance on Yale B database表4 在Yale B人脸数据集的AC聚类性能%

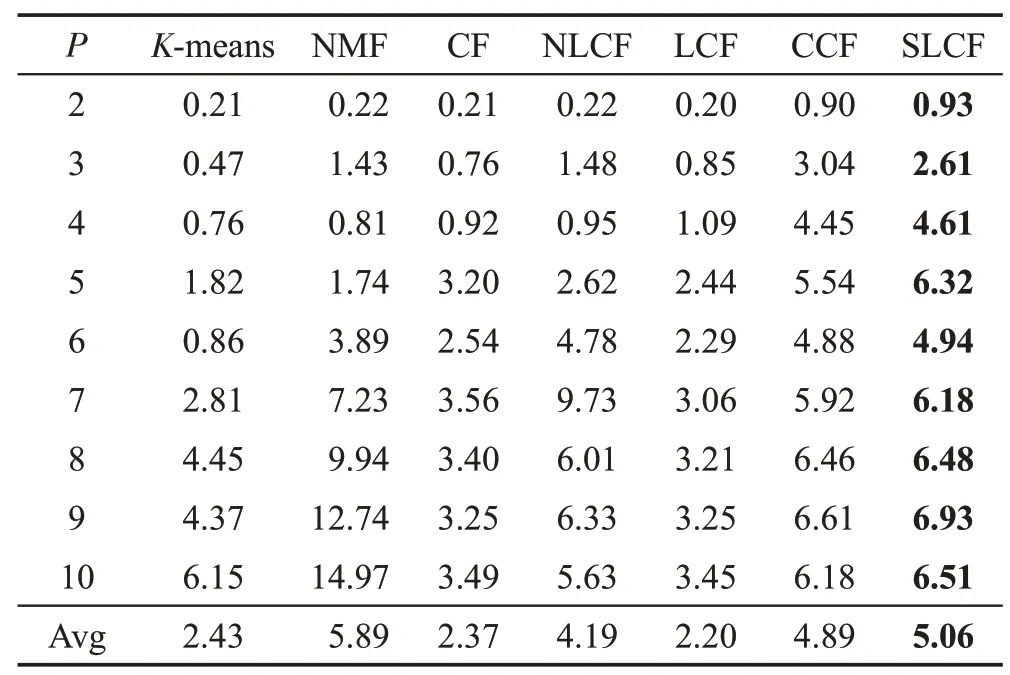
Table 5 Clustering NMI performance on Yale B database表5 在Yale B人脸数据集NMI聚类性能 %

从表4、表5中可以看出，CCF算法的聚类性能优于K-means、NMF、CF、NLCF及LCF方法。主要由于CCF为半监督学习方法，而K-means、NMF、CF、NLCF、LCF这5种算法均为无监督的学习方法，没有充分利用有效的标签信息。与CCF算法相比，SLCF在平均聚类精度AC上提高了0.39个百分点，在NMI上提高了0.17 个百分点，从而表明局部坐标约束能够提高算法的聚类性能。

4.3 在MNIST数据集上的实验

手写体MNIST数据集包含有60 000张图像的训练集和10 000张图像的测试集。图像分别为数字0～9共有10类，每张图像裁剪成28×28 像素。从前10 000个训练集中每类随机选择100 张图像组成的数据集进行实验，实验结果如表6、表7所示。

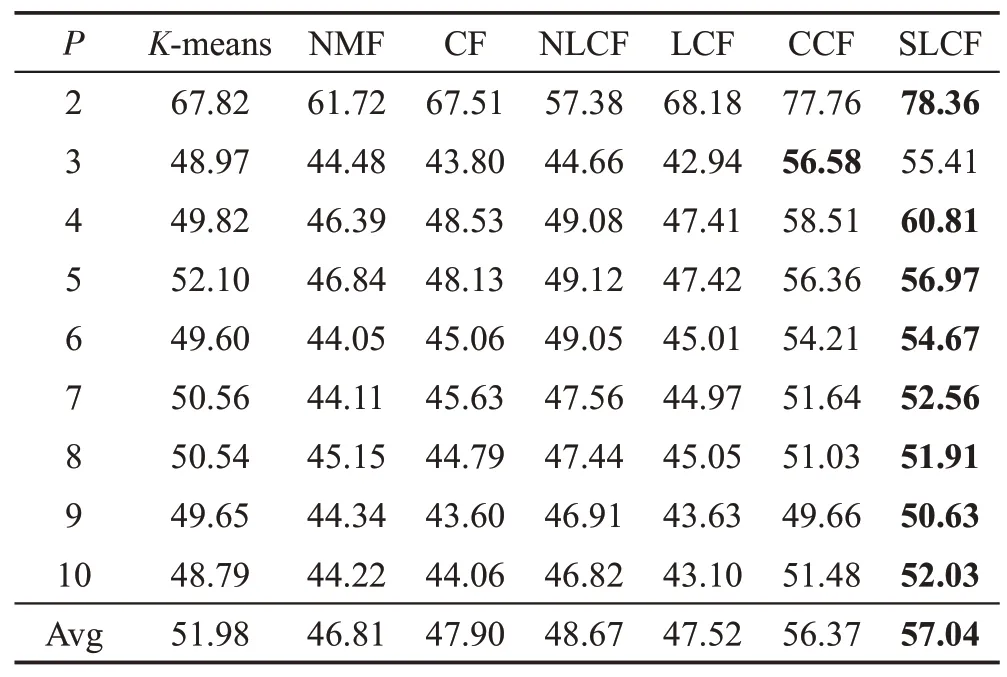
Table 6 Clustering AC performance on MNIST database表6 在MNIST数据集的AC聚类性能%

由表6、表7 可以看出，提出的SLCF 算法在不同的聚类数下的算法聚类性能优于其他比较的算法。具体来说，与NMF 算法相比，NLCF 在AC 上提高了2.85个百分点，在NMI上提高了1.86个百分点，主要由于NLCF 利用局部坐标约束提取了数据的稀疏性。与NLCF相比，SLCF算法在AC上提高了7.84个百分点，在NMI 上提高了8.37 个百分点，因为SLCF算法不仅考虑了数据的稀疏性，还有效地利用数据的部分标签信息，进一步提高了算法的聚类性能。

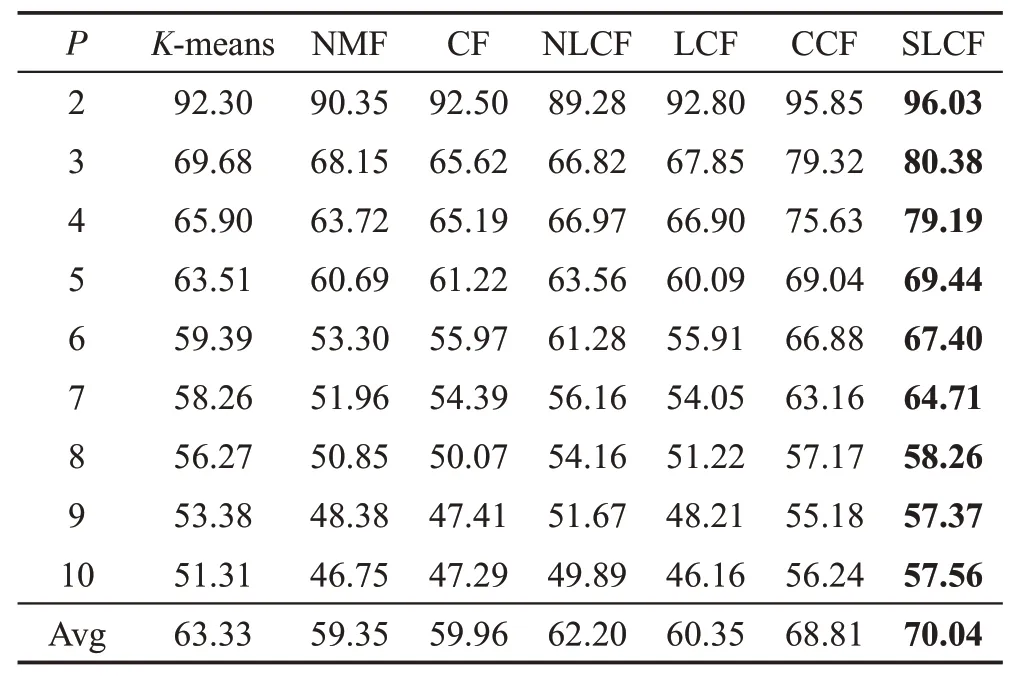
Table 7 Clustering NMI performance on MNIST database表7 在MNIST数据集的NMI聚类性能%

4.4 参数分析

下面讨论一下SLCF 算法中参数α对算法性能的影响情况。分别从COIL20、Yale B、MNIST数据库中随机选取5类所构成的数据子集X进行实验，且在Yale B 数据库中每类选取50 张图像，在MNIST 数据集中每类选取100 张图像。每个实验在选取不同的聚类数上独立运行10次，参数α分别从[10-3,10-2,10-1,100,101,102,103,104]变化的平均聚类性能结果如图1所示。从图1 中可以得到在本实验中NLCF、LCF 及SLCF 算法在不同数据库中参数α设置情况，如表8所示。由于算法K-means、NMF、CF以及CCF中没有任何参数，因此算法的性能并没有改变。

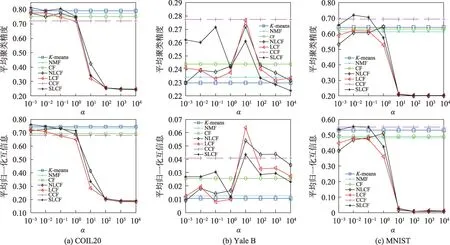
Fig.1 Clustering performance comparison with parameter α图1 参数α 变化的聚类性能比较图

Table 8 Parameter α in NLCF,LCF and SLCF表8 算法NLCF、LCF及SLCF中参数α 设置

提出的SLCF算法也是一个半监督学习方法，标签数据的比例与算法的性能具有密切的关系。为了讨论有标签数据的比例对算法性能的影响程度，随机选择每类有标签数据的比例分别从10%到80%的变化，每次实验独立运行10次，在不同的数据集上的实验结果如图2所示。从图2中可以看出，半监督学习算法CCF 和SLCF 算法随着有标签数据的比例增加算法的聚类性能逐渐提高。

4.5 收敛性分析

利用辅助函数法从理论上证明了SLCF 算法的收敛性。为了分析SLCF算法迭代更新的有效性，分别比较了CF、CCF 以及SLCF 算法在数据集上的收敛情况，比较结果如图3所示。

Fig.2 Effect of the number of labeled data on performance图2 有标签数据的比例对算法性能的影响

Fig.3 Convergence curves of CF,CCF and SLCF on 3 databases图3 CF、CCF、SLCF在3个数据集上的收敛曲线

从图3 中可以看出，不论从收敛速度上，还是精度上，SLCF 算法优于CF、CCF 算法，因此SLCF 算法的迭代更新过程是有效的。

5 结论

针对传统的概念分解算法不能利用有效的标签信息，也不能提取数据空间的稀疏性问题，本文将有限的标签信息和局部坐标约束融入到CF中，提出了一种带有局部坐标约束的半监督的概念分解（SLCF）算法。同时给出了SLCF算法的迭代更新规则，从理论上也证明了SLCF 算法的收敛性，在COIL20、Yale B 以及MNIST 数据库上实验表明提出的SLCF 算法是有效的。