引入通风力修正社会力模型的公路隧道人员疏散仿真研究*

刘心易，张玉春，蔡 鑫

(1.西南交通大学 地球科学与环境工程学院，四川 成都 611756;2.深圳市交通公用设施建设中心，广东 深圳 518032)

0 引言

公路隧道火灾事故频发，严重影响到隧道施工人员的生命安全[1]。当隧道火灾发生后，能够及时进行人员疏散至关重要。疏散过程受多种因素影响，准确把握各类影响因素是进行准确模拟的关键。随科技不断进步，计算机仿真模拟被广泛应用于人员疏散研究。

国内对公路隧道人员疏散安全研究主要集中于个人特征、隧道结构、车辆与人员关系等方面：向月[2]分析横通道宽度与设置间距对人员疏散时间的影响；周健等[3]与刘伟等[4]研究了9项个体因素对疏散时间及疏散结果的影响；陈诗明等[5]模拟分析车辆-人员荷载条件对疏散时间的影响；陈长坤等[6]基于性能化防火设计分析堵塞、火源位置等对疏散时间的影响。

社会力微观模型在人员疏散研究领域具有代表性，通过修正模型原始参数或引入其他项可应用于各类场景：焦宇阳等[7-8]将模型从2维特性应用于3维楼梯空间，通过利用模糊原则，关联恐慌与速度以优化火灾场景中人员疏散仿真；郭小林[9]通过引入视觉作用因子对期望速度和期望方向进行优化，建立教学楼应急疏散模型；Francesco等[10]引入转向因子，并假设疏散过程存在对场景熟悉的领导者带领人群疏散；Parisi等[11]通过引入自停机制模拟特殊行人流。此外，社会力模型还被应用于体育馆、机场、地铁站等公共场所的人员疏散。

根据JTG/T D70/2-02—2014《公路隧道通风设计细则》，火灾发生后隧道内存在不同程度通风作用力，隧道人员在疏散过程中必然受通风作用力影响，但现有研究未考虑通风作用力影响。本文通过引入通风作用力修正社会力模型，模拟在通风力作用下公路隧道人员的安全疏散。

1 引入通风作用力的社会力修正模型

1995年，Helbing等[12-13]基于流体动力学方程提出连续性微观疏散仿真模型即社会力模型，如式(1)所示：

(1)

式中：mi表示个体质量，kg；i，j代表不同行人；vi为行人i的速度，m/s；t代表某时刻，s；fwill为自驱动力，N；fij为行人间相互作用力，N；fiw为行人i与运动边界间相互作用力，N。社会力模型由自驱动力、行人间相互作用力、行人i与运动边界间相互作用力组成。个体在隧道内疏散时，通风作用力视为阻力。根据周雨青等[14]空气阻力计算人员疏散过程中所受通风力，如式(2)所示：

(2)

因此，修正后的社会力模型如式(3)所示：

(3)

式中：Fv为人员所受通风力，N；C为空气阻力系数，可视为摩擦阻力与其他阻力总效应，即C=C压+C摩+C其它，由于物体形状、运动速度大小和表面平整度不同，各阻力所占比重不同，但总和均为1；ρ为空气密度，kg/m3；S为人员迎风面积，m2；v为隧道内通风风速，m/s；vven为隧道内通风实时风速，m/s；vi(t)为行人i在t时刻速度，m/s；θ为行人i疏散方向与通风方向夹角，取值90°～180°。

2 模拟与结果分析

2.1 工况设置

基于改进模型的计算机仿真模拟以C语言为基础、VS2015+Qt为运行平台模拟隧道内人员疏散。模拟场景参考隧道内横通道间距设置，长L为250 m，宽W为7.5 m。火灾发生位置如图1所示，下游人员可直接乘车离开现场，上游人员位于最不利点(靠近但无法使用该横通道)，人员向左侧出口(横通道)步行疏散。通风方向指向火灾下游，与人员疏散方向相反。人员运动开始计时，运动至左侧横通道处计时结束。个体期望速度vi=1.5 m/s，松弛时间τi=0.5 s，空气阻力系数C=1.0，ρ=1.29 kg/m3。

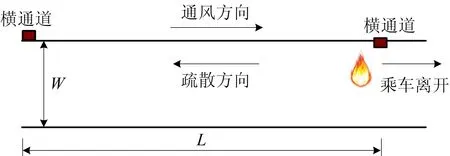
图1 模拟场景Fig.1 Simulated scene

为全面研究通风风速对疏散速度的影响，结合现行规范与徐志胜等[15]的理论计算，通风风速v取值0～6 m/s，每整数作为1种风速，共7组。通风力作用面为站立时正投影面，约占身体表面积30%～36%[16-17]，个体表面积与个体质量关系如式(4)所示：

(4)

式中：SA为个体表面积，m2。

为探讨个体质量mi与通风风速v的关系，设定质量20～90 kg，每10 kg 1组，共8组。

2.2 数据分析

利用引入通风作用力的社会力修正模型模拟不同隧道通风风速与个体质量工况，分析隧道通风风速与个体质量对人员疏散速度的影响。由图2可知，人员疏散速度在中间过程呈平稳直线，平稳过程中的疏散速度称为“平衡速度”，后文提到的疏散速度均为平衡速度。

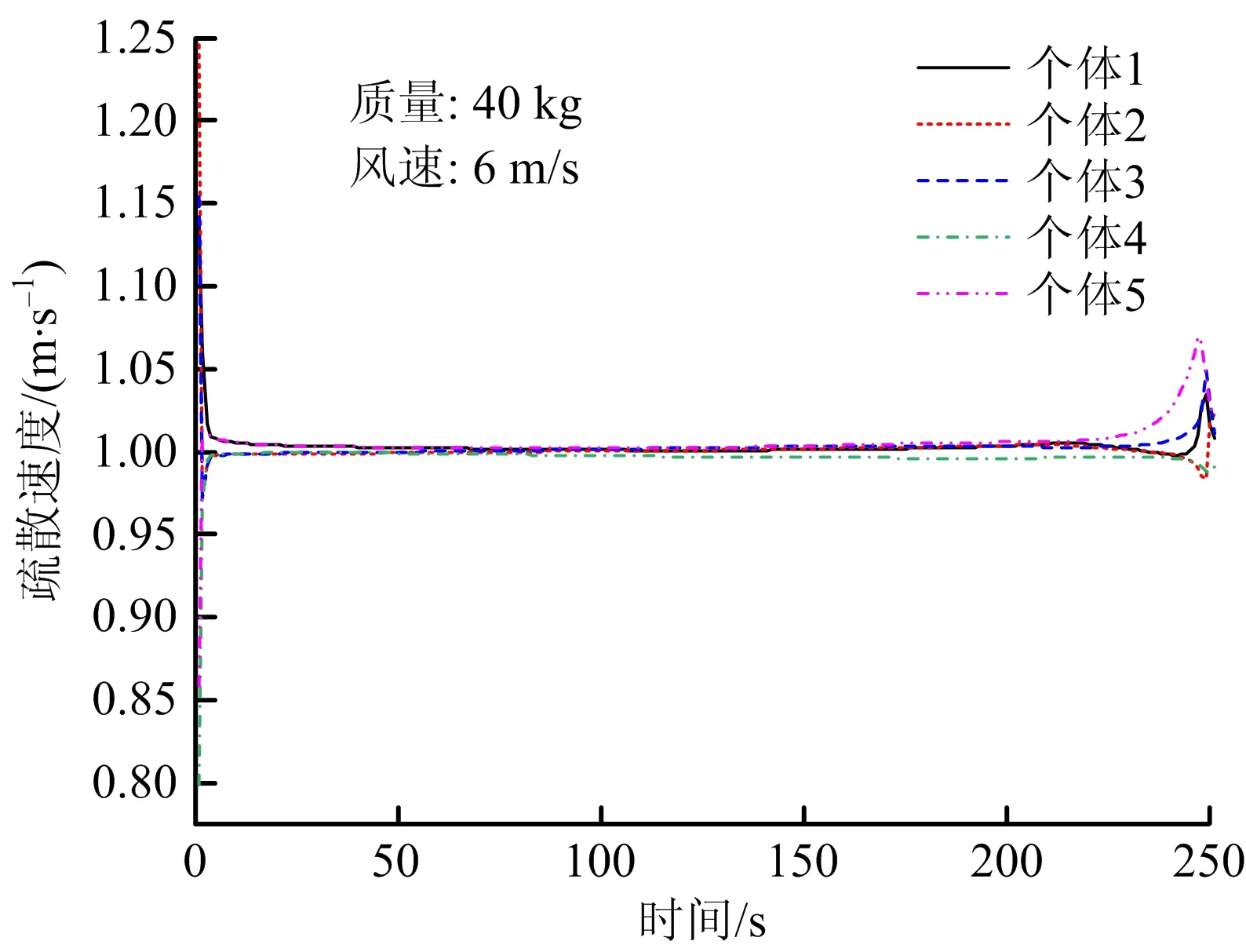
图2 部分工况个体速度变化Fig.2 Change of individual speeds under partial working conditions

结果表明：疏散速度随通风风速增大呈下降趋势，且下降幅度逐渐增大；疏散速度随个体质量变化受式(4)影响，在20～30 kg范围内随个体质量增加呈下降趋势，且降幅逐渐增大；在30～90 kg范围内随个体质量增加呈上升趋势，且上升幅度随质量增加而减小。个体质量较小工况下疏散速度随风速变化明显，个体质量90 kg曲线最平滑，受风速影响最小。不同个体质量工况下通风风速与疏散速度、速度变化率关系如图3～4所示。

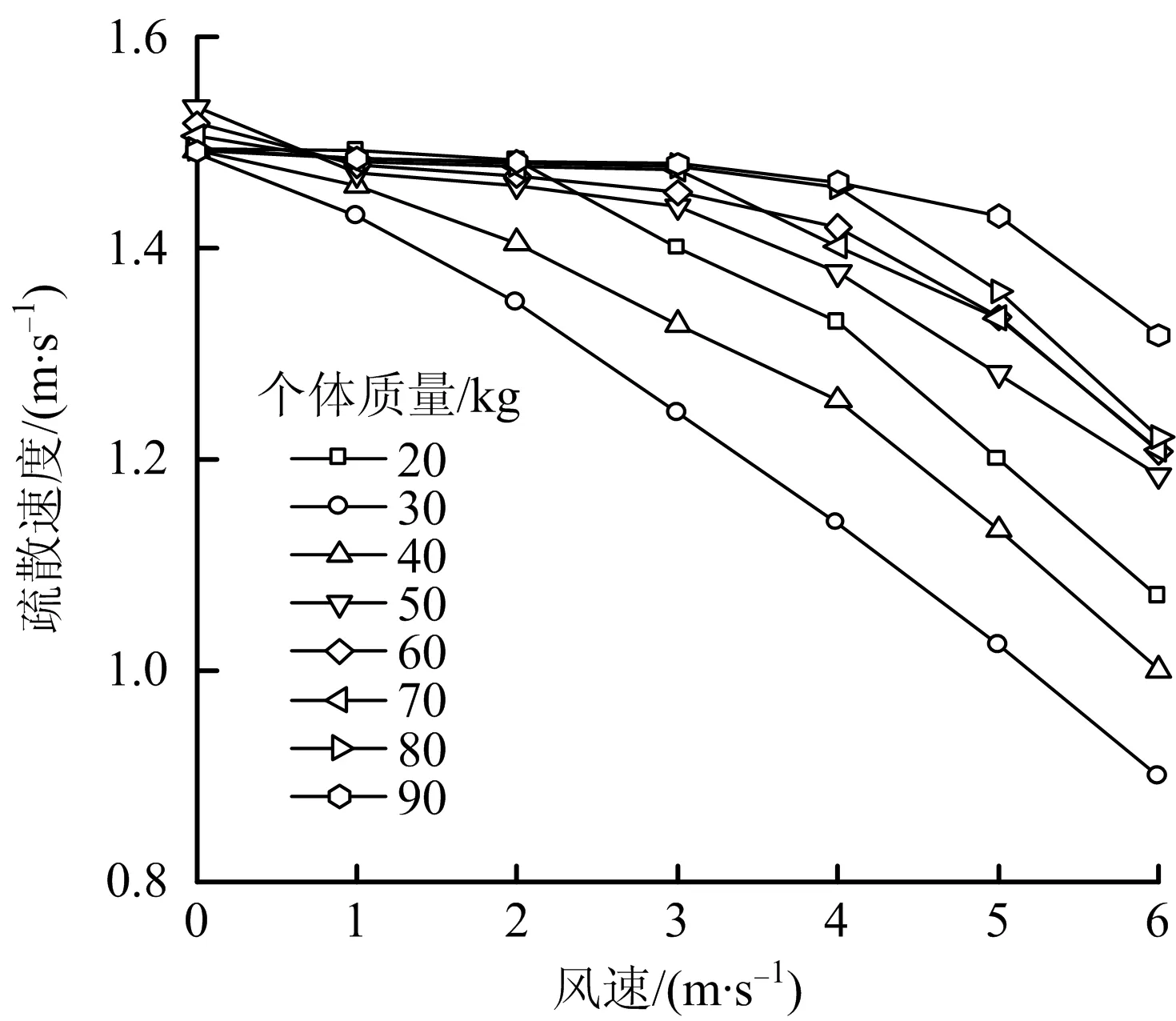
图3 不同个体质量工况下通风风速与疏散速度关系Fig.3 Relationship between ventilation wind speed and evacuation speed under different conditions of individual mass

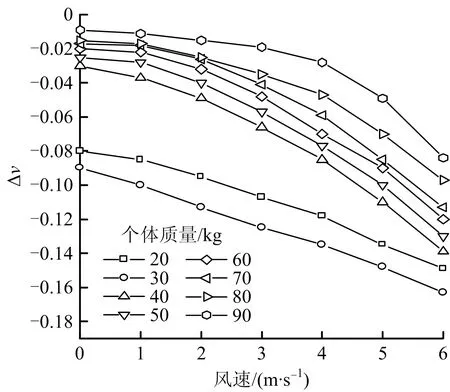
图4 不同个体质量工况下通风风速与疏散速度变化率关系Fig.4 Relationship between ventilation wind speed and change rate of evacuation speed under different conditions of individual mass

由图3～4可知风速与个体质量共同作用下疏散速度的变化。通风力作为阻力被引入社会力模型，通风风速增加使运动阻力增大，疏散速度必然降低；个体质量同时影响自驱动力与通风力，2种力变化幅度决定人员最终疏散速度变化。由式(2)和式(4)可知，以30 kg为分界点，通风风速相同时，质量最小个体(20 kg)疏散速度大于质量较大(30 kg)个体疏散速度。

2.3 结果讨论

根据模拟结果，从模型角度定性分析个体质量与通风风速对疏散速度的影响。通过利用社会力修正模型，定量分析不同个体质量与通风风速工况下疏散速度变化，验证社会力修正模型正确性与合理性。

在社会力修正模型中，疏散速度与各作用力如式(5)所示：

(5)

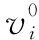
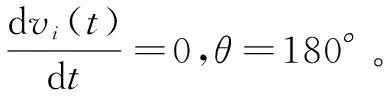
(6)

由mi和vven表示的平衡速度ve表达式如式(7)所示：

(7)

由式(4)～式(7)可知,平衡速度ve由个体质量与通风风速共同决定。

1)通风风速对疏散速度的影响

为考察通风风速vven对疏散速度的影响，对式(7)中vven求偏导，如式(8)所示：

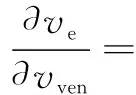
(8)

根据mi和vven取值范围(vven∈[0,6]，mi∈[20,30])，可知式(8)中mi≤30 kg部分如式(9)所示：

(9)

即平衡速度ve对通风风速vven的偏导函数恒小于0，个体质量在20～30 kg范围内平衡速度随通风风速增加而下降。

对mi>30 kg，如式(10)所示：

mi2<1.012mi2+0.008mi2vven+0.18mivven+0.27mi

(10)

由式(10)可知，个体质量>30 kg时，式(8)仍恒<0。所以在该质量范围内，平衡速度ve随通风风速vven增加而下降。研究结果与图3模拟结果基本一致。

为验证模型有效性与合理性，选取个体质量mi=50 kg，将通风风速分别代入式(7)与式(8)，得疏散速度与通风风速及2者变化速率关系如图5～6所示。由图5～6可知，随通风风速增加，疏散速度呈下降趋势，且下降幅度逐渐增加，与图3模拟结果基本一致。

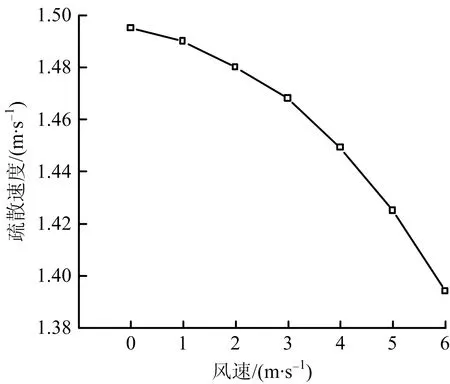
图5 mi=50 kg疏散速度随通风风速变化Fig.5 Change of evacuation speed with ventilation wind speed when mi=50 kg

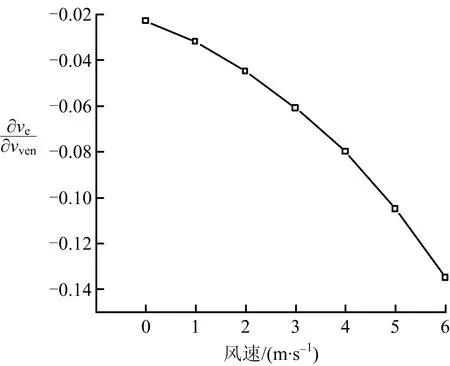
图6 mi=50 kg疏散速度随通风风速的变化速率Fig.6 Change rate of evacuation speed with ventilation wind speed when mi=50 kg

2)个体质量对疏散速度的影响

考察个体质量mi对疏散速度的影响，对式(7)中mi作偏导。由于原ve表达式较为复杂，求偏导函数时将后2项舍去以简化计算。对于mi>30 kg，根据mi及vven取值范围可知，2mi≫(0.008mi+0.18)vven，3mi≫(0.004mi+0.09)vven2，简化后如式(11)所示：

(11)

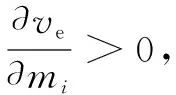
(12)

显然假设成立，疏散速度随个体质量增加而增加的假设正确，符合前文工况为30～90 kg疏散速度随个体质量变化趋势。同理，将风速vven=5 m/s代入公式验证，疏散速度与个体质量、疏散速度随个体质量变化速率关系如图7～8所示。由图7～8可知，疏散速度随质量增加呈上升趋势，但上升幅度逐渐减小。

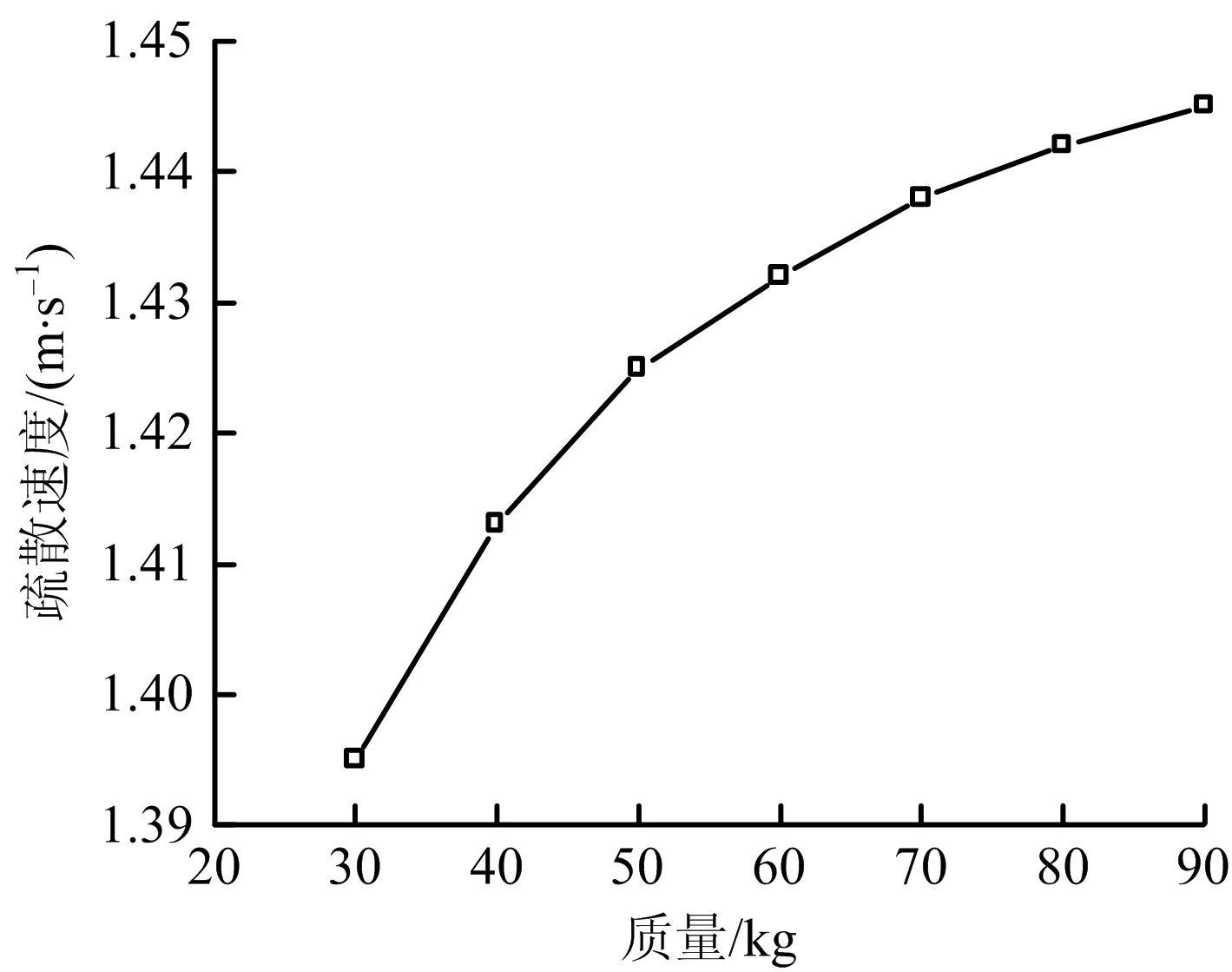
图7 vven=5 m/s时疏散速度随个体质量变化Fig.7 Change of evacuation speed with individual mass when vven=5 m/s

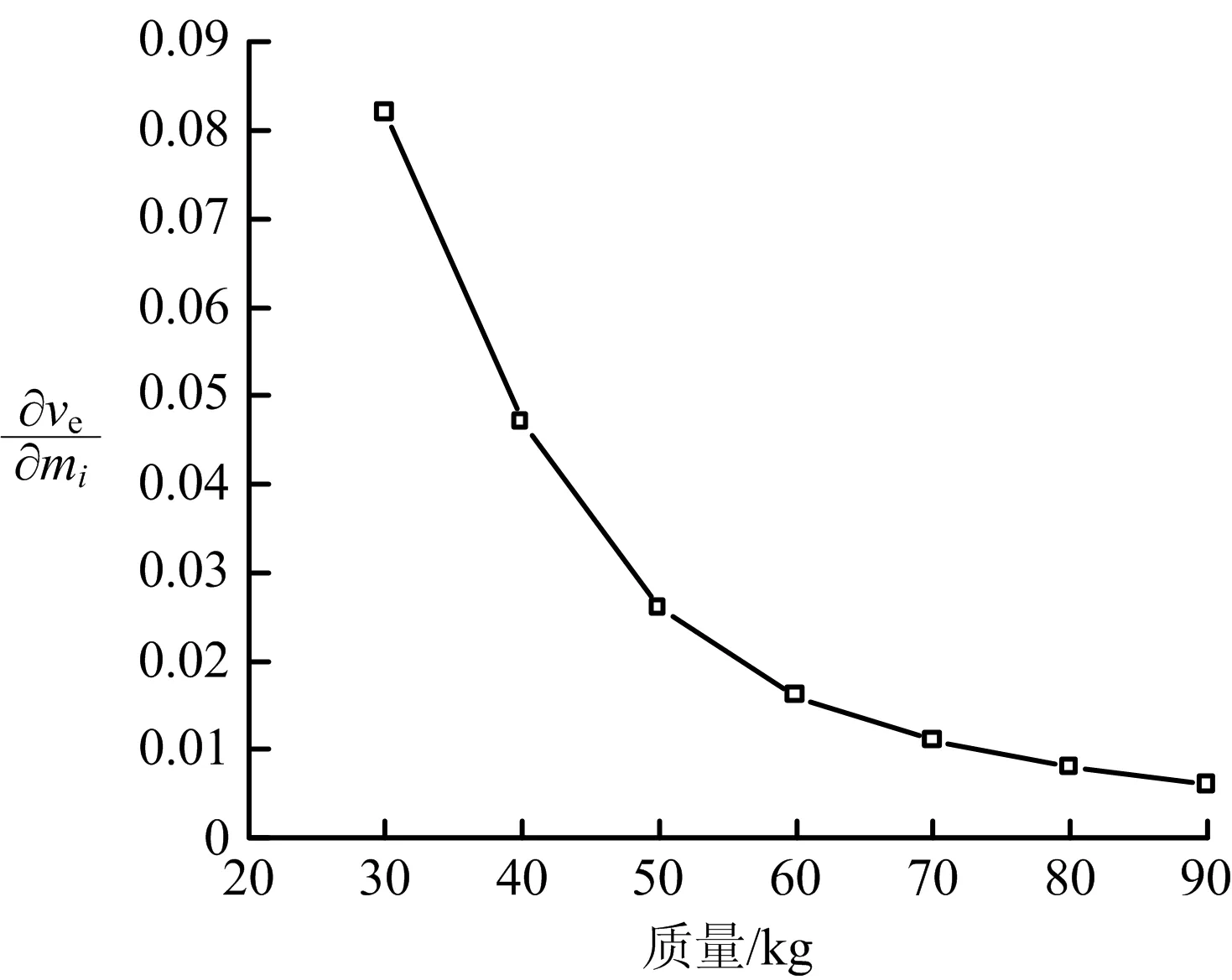
图8 vven=5 m/s时疏散速度随随个体质量的变化速率Fig.8 Change rate of evacuation speed with individual mass when vven=5 m/s

3 结论

1)与原始社会力模型相比，引入通风作用力的人员疏散速度变化明显，疏散速度由个体质量与通风风速共同决定。

2)受表面积表达公式影响，相同通风风速下，疏散速度随个体质量增加呈现上升或下降；个体质量为20～30 kg时，疏散速度随个体质量增加而下降，且变化幅度逐渐增加；个体质量为30～90 kg时，疏散速度随个体质量增加而上升，且变化幅度逐渐减小。即通风风速对疏散速度的影响在小质量个体工况更加明显；当个体质量为30 kg时，疏散速度最低。

3)个体质量不变时，通风速度增加，疏散速度下降，且通风风速越大疏散速度下降越明显。

4)本文考虑到除性别、年龄其他可能影响疏散速度的因素，可以为隧道人员疏散方案制定提供理论依据。