基于改进LS-SVM 算法的列车通信网络时延预测方法

汪知宇 张 彤

（大连交通大学电气信息工程学院，116028，大连；2.大连交通大学机车车辆工程学院，116028，大连∥第一作者，硕士研究生）

列车通信网络（TCN）是列车的关键系统之一，被称为列车的“心脏”和“大脑”。由于TCN 在运行过程中存在通信协议转换、运行环境多变等影响因素，使信号在传输过程中不可避免的产生时延。网络诱导时延对TCN 的控制作用产生较大影响，使数据无法及时传输，时延过大将会导致列车无法及时进行牵引、制动，同时对旅客舒适度及旅客安全产生影响。因此，分析和预测网络时延对TCN 系统有着至关重要的作用［2］。目前较为常用的随机时延预测方法有：最小均方算法、经验模式分解算法、最小二乘法支持向量机（LS-SVM）算法、神经网络算法等［3-5］。文献［6］采用了基于Elman 神经网络算法对时延进行预测，此方法适应时变能力的特性较好，但精度不足以满足实际需要。文献［7］采用了基于RBF 神经网络的预测算法，虽然可以任意精度针对任意非线性函数进行逼近，但神经网络具有有限的泛化能力，容易得到局部极小值。文献［8］采用了未经改进的LS-SVM 算法对时延进行预测，由于参数无法确定，预测精度不好掌控。基于以上分析，本文提出了基于改进PSO（改进粒子群）算法的LS-SVM 算法对TCN 时延数据进行预测［9-10］。首先，在所搭建的TCN 半实物仿真平台上，分别改变源端口特征周期及端口数量抓取了大量时延数据；利用了PSO 算法来优化LS-SVM 算法的可调参数及平方带宽；最后，与传统的LS-SVM 算法及Elman 神经网络算法进行对比分析，验证了该方法的有效性。

1 TCN 平台搭建与时延测试

TCN 时延测试平台采用TCN 技术搭建符合IEC-61375 协议标准，通过MVB（多功能车辆总线）对各子系统进行连接，完成了设备之间的数据通信。网络控制系统设备包括：VCU（车辆控制单元）、REP（中继器）和HMI（人机接口界面）。使用TCN 分析仪抓取时延数据，通过PC 机对时延数据进行监测。为了实现通过TCN 平台的时延进行测试，采用Unicap 组态软件对各控制单元软件进行开发，对输入模块及输出模块进行程序编写。

TCN 时延实质上是整个TCN 的信息交互时间，其中包括了发送时延、传输时延、接收时延，而发送时延又包括处理时延、等待时延、应答时延。同时通信设备、通信距离等因素都会对时延数据产生影响，TCN 的总体时延等于各部分时延数据之和。时延的产生主要包括以下部分［6］：

1）源端口进行数据发送所消耗时间（与数据包长度有关）。

2）数据在传输过程中所消耗的时间（与MVB长度有关）。

3）通信寄存器进行数据收发及处理的排队等待时间。

为了避免其他设备属性对数据产生影响，保持其他属性不变，只使用VCU、HMI 等网络设备。现设计如下的时延测试基本步骤：

步骤1：通过UNICAP 软件编写HMI 及VCU组态程序，分别取多组不同特征周期及不同端口数量的时延数据进行分析及预测，将组态软件程序通过MVB 下载到VCU 及HMI 中。时延传输过程如图1 所示。

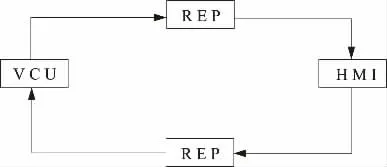
图1 时延数据传输过程

系统总时延即各设备时延数据之和：

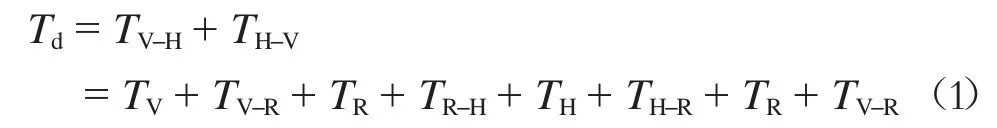
式中：

Td——系统总时延；

TV-H——VCU 到HMI 之间的时延；

TH-V——HMI 到VCU 之间的时延；

TV-R——VCU 到REP 之间的时延；

TR-H——REP 到HMI 之间的时延；

TH——数据通过HMI 产生的时延；

TV——数据通过VCU 产生的时延；

TR——数据通过REP 产生时延。

试验平台通过TCN 进行搭建，使过程数据在设备之间进行通信。

步骤2：通过IPTDM2 软件与PTS402 配置软件一起使用，采用IPTLMlog 工具来对TCN 采集数据，收集通过MVB 得到的数据帧并形成数据文件。图2 为通过抓包软件得到的数据解析图，是利用TCN 分析仪抓取的时延数据包。通过IpTLMview工具对所收集到的图形数据进行读取及解析，从中可以看到各端口过程数据发送时间及接收时间。通过查找发送及接收端口号对应的时间数据，对数据包进行统计及计算。传输过程中数据通过VCU、REP 和HMI 模拟形成一个VCU 到HMI 之间的网络控制系统。其中，一台PC 机控制VCU 数据发送，使用网络分析仪接入模拟系统中对时延数据进行抓取；另一台PC 机对网络分析仪抓取到的数据量进行控制。

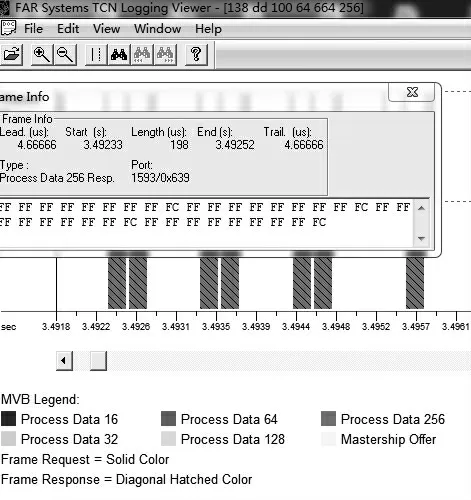
图2 数据解析实景图

2 基于PSO 算法的参数优化

2.1 LS-SVM 算法分析

LS-SVM 算法是一种新型的支持向量机算法，该方法用等式约束替代SVM 算法中的不等式约束，将求解过程转变为对等式方程的求解问题，使算法的运算速度加快；通过结构风险最小化原则增加了算法的泛化能力，解决了局部最小值等问题。因此，使用LS-SVM 算法对非线性函数进行预测，可以得到较好的预测效果。其回归函数为

式中：

u——惯性权重系数；

b——偏置。

对于给定的训练集（xi，yi），i = 1，2，…n，其中xi∈R，yi∈R（R 为实数）。LS-SVM 定义如下：

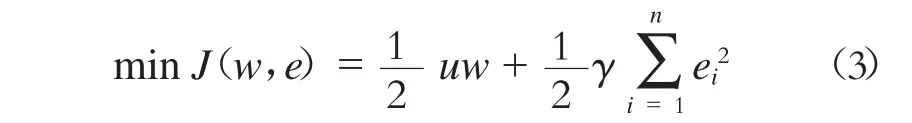
式中：

w——惯性权重；

γ——正则化参数；

ei——LS-SVM 中的损失函数， 需要满足以下条件：

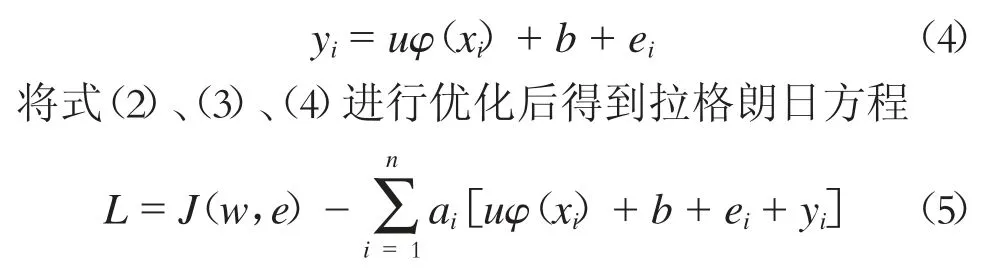
式中，ai为系数。

由Karush-Kuhn-Tucker 优化法可知，通过对w、b、e、a 求偏微分，可以得到最优值。求解偏微分步骤如下0 ，得w == 0 ，得w ==0；=0，得ai=ce（ic 为系数）；=0，得uφ（xi）+b+ei+yi=0。

消除w 和e，得到回归函数方程为

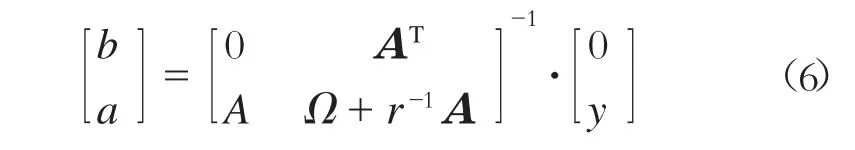
式中：

Ω——核函数；

A——相应维数的单位矩阵。则LS-SVM 预测模型为

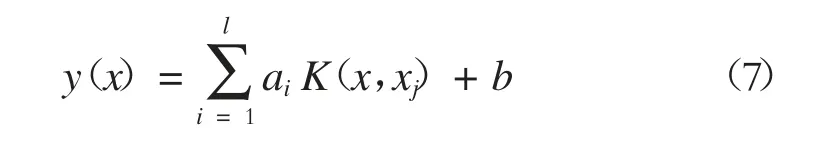
式中：

K（x，xj）——把样本映射到特征空间的核函数；

xj——第j 个支持向量的位置输入。

2.2 基于PSO 算法迭代优化LS-SVM

LS-SVM 算法模型需要对γ 及平方带宽σ 进行调节。这2 个参数在很大程度上决定了LS-SVM算法的学习及泛化能力。假设γ 与σ 的取值范围均为0 到500，则计算时间将达到数十h。如果将PSO算法引入，将会在参数选取、收敛速度方面具有一定的优势［11］。通过对PSO 算法研究，结果发现存在误差的粒子群将会降低收敛时间，加快运行速度，但有可能错过了最优解。因此，本文提出了一种改进的粒子群优化模型，粒子群比较了状态最优解与全局最优解，根据方程（8）、（9）、（10）来调节迭代状态，更新位置及速度。权重调整公式如（8）、（9）、（10）所示：

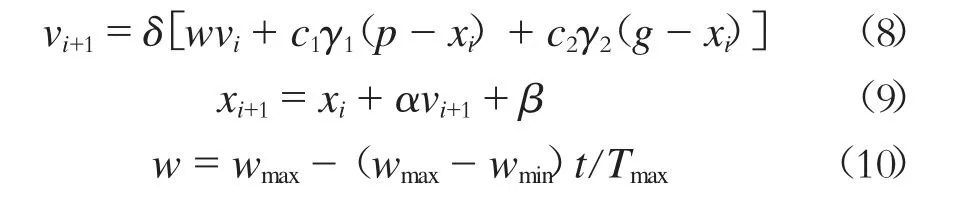
式中：

vi+1、vi——分别为第i+1、i 个粒子的速度；

xi+1——第i+1 个粒子的位置；

t——当前迭代次数；

γ1，γ2——范围在［0，1］之间的随机数；

c1，c2——范围在［0，2］之间的随机数；

g——全局最优位置解；

Tmax——最大迭代次数；

p——状态最优解；

α——局部搜索因子；

β——微调因子；

δ——速度调节因子。

在第t 次迭代中，对w 进行调整。当迭代次数增加时，w 将减少，使优化过程更加准确。同时本文加入α 及β 对模型进行改进，实质上在每次位置更新后，δ 将本次的搜索速度当成新的搜索范围。如果更新后的搜索位置优于当前搜索位置，则将更新后的位置作为开始点；否则，继续使用原位置。

本文采用高斯函数作为仿真试验的核函数。由于核函数的参数σ 和LS-SVM 算法的可调参数会影响算法的性能，因此采用PSO 迭代算法对参数进行寻优，可在很大程度上提高模型的精度。将时延数据分为测试样本和训练样本，具体步骤如下：

1）对粒子群参数包括迭代次数T、粒子位置属性δ 及速度属性σ2进行初始化；

2）当粒子的当前速度比前面最好位置出现的适应度小时，就作为最好的位置p；

3）当粒子经过的位置比最优位置对应的位置g的小时，则作为最优位置g；

4）根据粒子的变化速度vi+1，得到新的种群，输入测试样本进行预测。

3 仿真试验方案

根据搭建好的半实物平台，分组对不同情况下的时延数据进行测试，并对得到的时延数据进行分析，针对不同特性的数据进行预测仿真，以此来验证本文所采用算法的有效性。

3.1 时延数据特性分析

对TCN 时延数据进行抓取。为了避免其他设备属性对特征周期产生影响，保持其他属性不变，只增加源端口发送周期。统一设置抓取时间为60 s，进行分组测试，试验数据见表1。表1 中分别分3 组对源端口不同特征周期下的最大时延、最小时延及平均时延进行整理及计算，并统计出不同情况下的过程数据包请求个数、过程数据包响应个数及负载率大小。时延趋势变化对比如图3 所示。经过分析得出，当保持其他参数不变时，只增加源端口特征周期，使数据解码及数据访问时间发生变化，从而导致系统时延增加。同时特征周期的增加导致端口被轮循的次数减少，因此负载率降低。

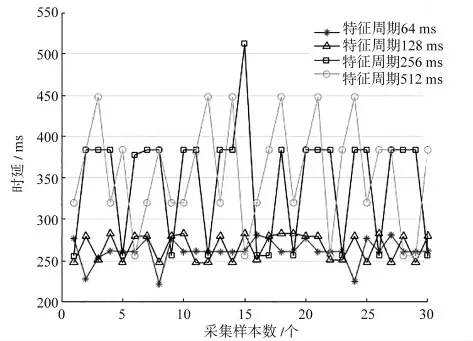
图3 不同特征周期对时延数据影响（端口数为138 个）

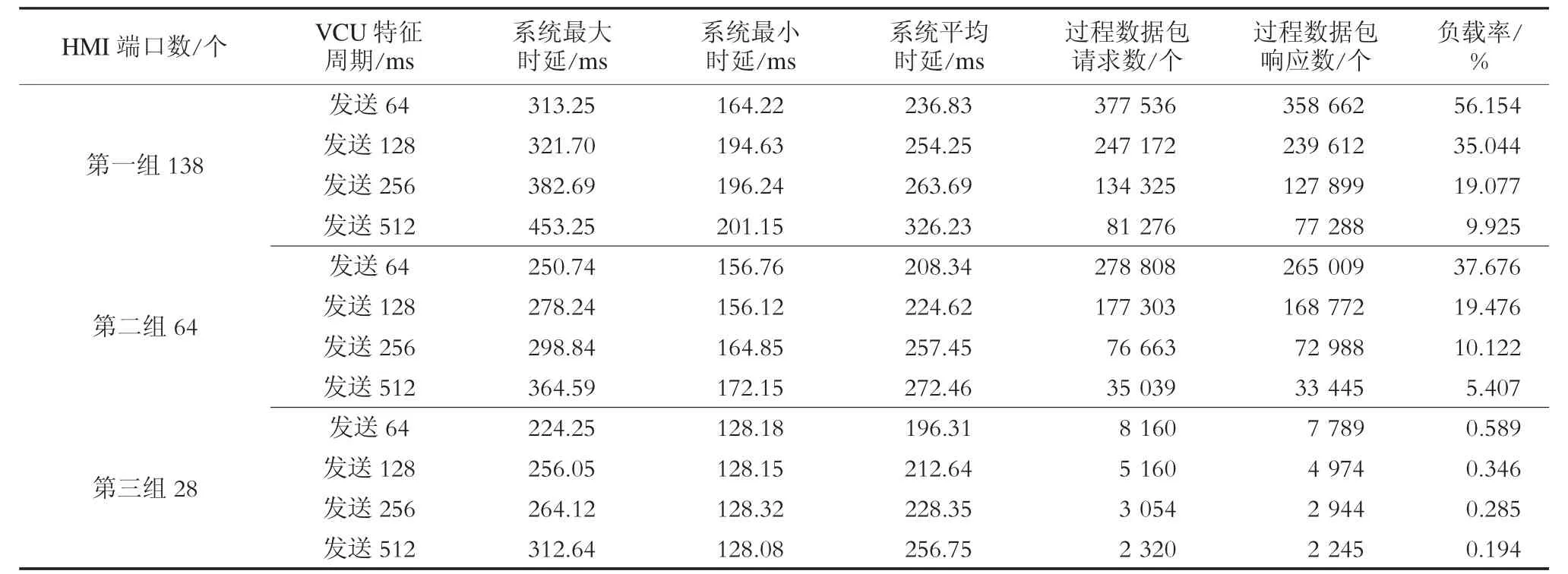
表1 不同源端口特征周期时延数据对比

当保持其他属性不变，只改变端口数量，进行分组测试，试验数据见表2，时延趋势变化对见图4。从图4 中可以看出，当保持其他参数不变时，只增加端口数量，导致时延数据变大，同时负载率增加。这样就增大了控制信号反应时间，降低了数据传输的实时性，最终影响了TCN 数据的及时传输。

表2 不同端口数的时延数据对比

3.2 时延预测仿真

针对不同情况下时延变化情况，进行时延预测仿真。利用试验平台测试得到550 组前向时延数据，前500 组作为训练样本，后50 组作为测试样本。使用Matlab 软件进行仿真试验，训练得到对应的参数。设置粒子位置属性γ 范围为［0.01，300］、速度属性σ 范围为［0.1，1 000］，仿真得到LS-SVM 中γ 为0.931 4，σ 为8.159。为了进行预测结果精度对比，本文将预测结果与Elman 神经网络算法及未经优化的LS-SVM 算法预测结果进行比较，结果如图5、图6、图7、图8 所示。

生成训练样本和测试样本后，通过改进PSO 算法迭代寻优，搜索参数初始值如表3 所示。

通过比较得出本文所采用的基于PSO 迭代优化LS-SVM 算法适用于不同特性的时延数据的预测，而Elman 神经网络算法及LS-SVM 算法均无法达到理想的预测效果。为了对三种方法进行定量评定，从运算时间、均方误差和绝对误差率3 个方面进行对比，如表4 所示。

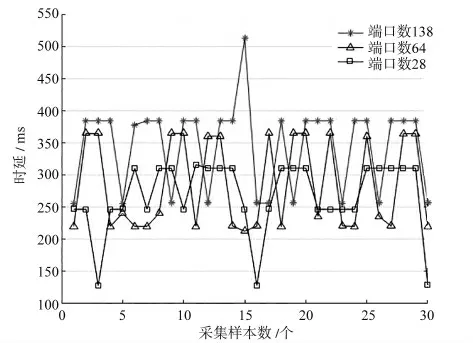
图4 不同端口数对时延数据的影响（特征周期为512 ms）

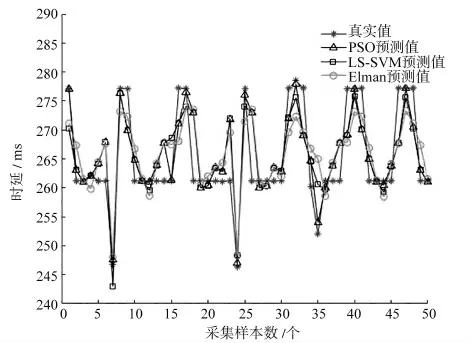
图5 端口数为138 个、VCU 特征周期为64 ms 时的时延预测仿真图

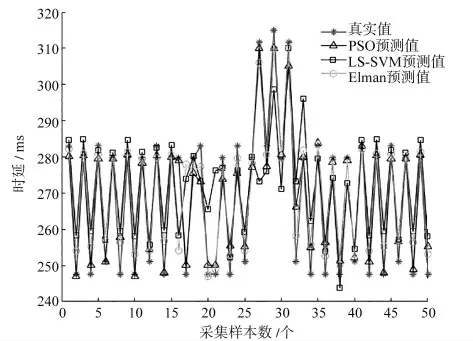
图6 端口数为138 个、VCU 特征周期为128 ms 时的时延预测仿真图

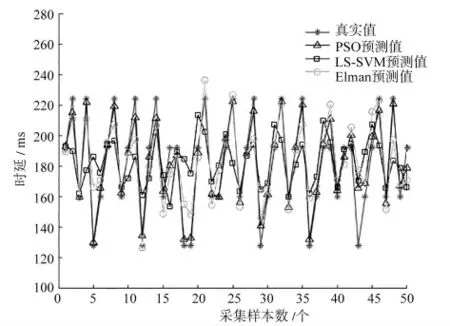
图7 端口数为28 个、VCU 特征周期为64 ms 时的时延预测仿真图

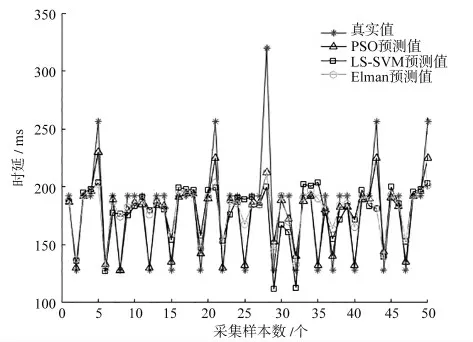
图8 端口数为28 个、VCU 特征周期为128 ms 时的时延预测仿真图

表3 PSO 算法参数初始值

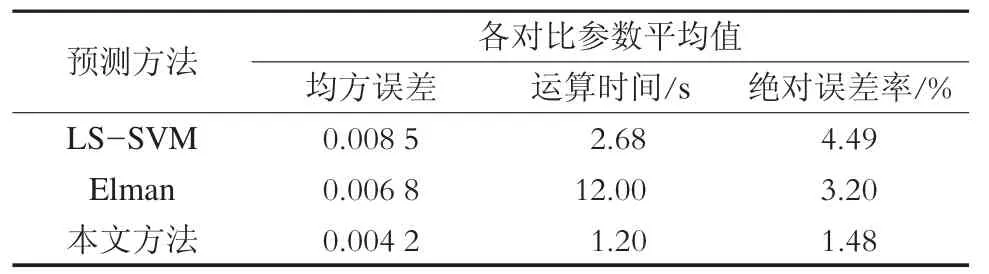
表4 3 种预测方法的相关参数平均值对比

从表4 中可以看出，本文采取基于PSO 迭代优化的LS-SVM 算法节约了运算时间，同时预测精度也有大幅度提高。使用LS-SVM 算法预测时，由于γ 及σ 直接对预测效果产生影响，而本文算法不但避免了局部极小值问题，同时解决了计算复杂度高、运算速度慢等问题。因此，可得出本文预测方法适用于TCN 控制系统的时延数据及高实时性、高精度数据的预测。

4 结语

在对试验平台进行搭建后，进行时延测试，通过MVB 对时延数据进行抓取，得到大量有效的时延数据，并对时延数据进行统计，分析其时延变化特点。本文提出基于改进的PSO 算法迭代来优化LSSVM 算法对TCN 时延进行预测，试验结果表明本文方法在预测精度及预测速度上较其他方法有大幅度提升，对于TCN 时延的预测具有良好的效果，为TCN 时延补偿得到了大量有效数据。