基于特征约简与选择性集成算法的城市固废焚烧过程二噁英排放浓度软测量

汤 健乔俊飞徐 喆郭子豪

(1.北京工业大学信息学部,北京 100124;2.计算智能与智能系统北京市重点实验室,北京 100124)

1 引言

城市固废焚烧(municipal solid waste incineration,MSWI)在生活垃圾的无害化、减量化和资源化处理等方面优势显著.MSWI过程排放被称为“世纪之毒”的痕量特性污染物二噁英(dioxin,DXN)[1],其在生物体内具有显著地积累和放大效应,对生态环境与人类健康具有巨大危害[2].目前,DXN排放浓度还无法在线实时检测,其产生机理至今仍不清晰,难以建立数学模型[3].通过利用高浓度的单氯苯等关联指示物进行DXN排放浓度的在线间接检测是目前研究热点之一[4-8];但该方法所具有的时间滞后性难以满足MSWI过程运行优化与反馈控制的要求,并且关联模型低精度、检测设备的高复杂性和低性价比等原因导致该方式难以实际应用.目前工业界多采用具有周期长、滞后大、成本高等缺点的在线采样-离线化验相结合的方法[3],即:以月/季周期或不确定周期由具有资质的检测机构在现场人工采样若干小时、在实验室离线化验至少一周、单次采样化验费用为0.5～1万元.显然,上述方式不能支撑以降低DXN排放浓度为直接设定目标的MSWI运行优化与反馈控制.数据驱动软测量技术常用于在线获得依靠离线化验或专家推断等方式才能获取的难以检测过程参数测量值[9-10].MSWI过程的炉内温度、炉排速度、一/二次风量、烟气压力/温度、活性炭量等过程变量以及SO2,HCl等污染气体的浓度,以秒为周期基于分布式控制系统和在线烟气检测系统进行采集;但排放烟气中的DXN浓度却以月/季周期或不确定周期基于实验室离线化验获得.显然,通过过程变量和DXN排放浓度的时序匹配仅能获得少量有标记建模样本.此外,MSWI全流程过程变量间存在较强共线性.因此,DXN排放浓度的软测量需要面对特征约简和小样本数据非线性建模等问题.

基于国外机构采集的关键过程变量进行DXN排放浓度预测的研究包括:文献[11]针对不同类型的焚烧炉构建线性回归模型;文献[12]构建基于遗传编程的非线性模型,结果表明预测性能强于多元线性回归和误差逆向传播神经网络(back propagation neural network,BPNN)模型;为进一步提高模型泛化性能,文献[13]构建基于最小二乘-支持向量机(least squaressupport vector machine,LS-SVM)的预测模型.采用国内MSWI过程数据,文献[14]提出采用遗传算法优化BPNN模型的软测量策略,但该方法所固有的随机特性导致难以针对小样本数据获得稳定的预测性能;针对上述问题,文献[15]提出对小样本数据进行重新抽样和噪声注入以增加样本数量,再构建基于最大熵神经网络的DXN排放浓度预测模型的策略.上述方法存在难以处理高维特征、面对小样本数据时预测性能稳定性差等问题.

研究表明,潜结构映射算法(projection to latent structure,PLS)及其核版本能够提取线性/非线性潜在变量构建模型,具有能够消除高维输入特征间的共线性、降低对建模样本数量要求等优点[16];但存在过多的输入特征会降低模型的泛化性能和可解释性、适合建模样本特性的核参数难以有效选择等问题[17].针对高维近红外谱数据,文献[18]提出组合特征选择与核潜结构映射算法的建模策略,有效提高了模型的预测性能;但其仅构建了泛化性能有待提升的单一模型,并不适用于小样本数据.研究表明,基于选择性集成(selective ensemble,SEN)算法的软测量模型具有较佳的泛化性和鲁棒性[19].基于“训练样本重采样”集成构造策略的SEN算法验证了集成部分可用候选子模型可获得比集成全部候选子模型更好的泛化性能[20],但所采用的BPNN算法并不适合于小样本数据建模.面向小样本高维频谱数据,文献[21]提出了综合考虑多源多尺度特征和多工况样本的双层SEN潜结构映射建模策略,但该方法所构建软测量模型存在复杂度高、普适性弱等缺点,同时也未进行维数约简.因此,将维数约简、核参数自适应选择、模型复杂度可裁剪等功能为一体的SEN策略,应用于DXN排放浓度软测量的研究未见报道.

综上,针对DXN 排放浓度建模数据所固有的高维、小样本、共线性和非线性等特性,本文提出了基于特征约简与SEN算法的软测量方法.对预处理后的建模数据采用变量投影重要性(variable projection importance,VIP)和输入特征约简比率进行维数约简,基于预先给定训练子集数量、候选子模型的结构参数及候选核参数,构建候选子模型并对其进行评价,并基于集成子模型选择阈值和加权算法进行集成子模型的选择与合并,对基于全部候选核参数的SEN核潜结构映射模型采用性能最佳准则获得最终DXN模型.采用文献和国内某MSWI厂多年的DXN排放浓度数据验证了所提方法的有效性.

2 面向DXN排放的MSWI工艺描述

MWSI包括固废储运、炉内焚烧、蒸汽发电、烟气处理等阶段,其中:焚烧炉将固废转变为灰烬、烟气和热量,底部炉排促使固废在燃烧室内移动以使燃烧更为有效和充分,余热锅炉产生用于发电的蒸汽,烟气处理设备清除焚烧烟气中的部分污染物.

从产生机理的视角,DXN排放浓度与炉内焚烧和烟气处理阶段的过程变量和排放至大气中的易检测气体浓度等相关,如图1所示.

图1表明,MSWI包括DXN的产生、吸收和排放共3个阶段.在焚烧炉和余热锅炉的“加热-燃烧-冷却”阶段,为保证有机物的有效分解,通常要求焚烧炉内的烟气达到至少850◦C并保持2 s;机理研究表明,预热区域(20◦C～500◦C)、高温转换区域(800◦C～500◦C)和低温转换区域(500◦C～250◦C)等均与DXN产生密切相关[22],不同温度区域的产生机理也具有差异性;特别是在烟气冷却阶段,某些被分解的DXN也可能会重新生成.显然,作为DXN产生阶段产物的烟气G1具有外部可测的最大DXN浓度,但目前MSWI企业均未对其进行监测.在烟气处理阶段,石灰和活性炭被喷射进入反应器以去除酸性气体和吸附DXN及某些重金属,进而使得G1烟气中的DXN被分为两部分:一部分被吸附后进入飞灰储仓;另一部分经袋式过滤器过滤后留存于烟气G2中,通过引风机排入烟囱进而作为烟气G3排放至大气中.因此,理论上DXN是与焚烧过程和烟气处理过程的众多变量,以及CO,HCl,SO2,NOx和HF等气体浓度相关.图1表明,MSWI的过程变量和其排放的易检测气体浓度以秒为周期在线实时采集,但DXN排放浓度需通过至少1周的时间才能获得离线化验值.可见,DXN排放浓度软测量面对的是特性难以描述的小样本高维数据.此外,DXN生成和吸收阶段的机理复杂不清,不同阶段过程变量的特性也存在差异性,这些因素导致难以进行基于机理知识的特征选择.因此,基于约简特征构建基于“训练样本重采样”集成构造策略的SEN模型可有效用于DXN排放浓度的预测.进一步,待构建的预测模型可表示为

图1 面向DXN排放的城市固废焚烧(MSWI)过程描述Fig.1 DXN emissions-based municipal solid waste incineration(MSWI)process description

3 软测量策略及实现

本文提出的DXN排放浓度软测量策略包括数据采集与预处理、基于VIP的特征约简和基于训练样本集成构造策略SEN软测量模型共3个模块,见图2.

3.1 数据采集与预处理模块

将DXN产生阶段、吸收阶段和排放阶段在线采集的与DXN排放浓度相关的过程变量或易检测气体排放浓度确定为输入特征,结合DXN排放浓度的离线化验值构建建模数据的输入输出样本对,并进行离群点和缺失值的处理.全部建模样本可表示为

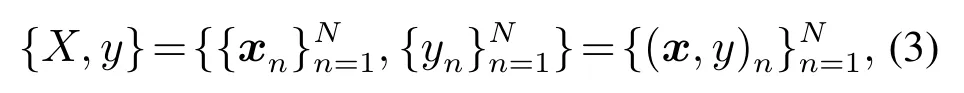
其中X ∈RN×M和y ∈RN×1表示用于构建DXN 排放浓度模型的输入和输出数据.

3.2 基于VIP的特征约简

首先构建基于全部输入特征的线性潜结构映射模型,再计算这些输入特征的VIP值并对其进行排序,最后基于依据经验设定的特征约简比率值选择输入特征.PLS算法通过最大化输入输出数据间的协方差在新的潜在变量空间构建具有线性结构的多层回归模型,其层数即为潜在变量(latent variable,LV)的数量.算法描述如下所示.

图2 软测量策略Fig.2 Soft sensor strategy

算法1线性PLS算法.

输入:输出矩阵X.

输出:输出矩阵Y.

由以上算法描述可知,线性PLS算法的外部模型用于提取和输入/输出空间均相关的潜在变量,内部模型通过这些LV构建回归模型,其可表示为

表示与算法1中的向量所相应的矩阵;H为LV的数量.

VIP指标能够表征每个输入特征对模型性能的影响,以第mth特征为例,其计算式如下:

3.3 基于训练样本集成构造的SEN软测量模型

首先采用操纵训练样本的集成构造策略产生训练样本子集并基于候选核参数和结构参数值构建候选子模型,接着对候选子模型进行评价并基于选择阈值获得集成子模型,然后对基于相同核参数的集成子模型进行加权以获得模型输出,最后基于预测性能获得最终的DXN软测量模型.主要步骤描述如下.

1) 训练子集构造.

基于“训练样本采样”方式从训练样本{(xSel,y)n}中产生数量为J的训练样本子集,即集成构造,可表示为

上述DXN预测模型的构建如图3所示.

图3 基于训练样本集成构造的SEN软测量模型构建流程Fig.3 SEN soft sensor model construction process based on training samples ensemble construction

4 实验验证

4.1 国外文献数据验证

1) 数据描述.

利用水冷壁焚化炉数据[12-13]构建DXN排放浓度模型,其输入特征按编号从1-8依次为:蒸汽负荷(tone/h)、烟气中H2O含量(%)、烟道温度(◦C)、烟气流量(Nm3/min)、CO浓度(ppmv)、HCl浓度(ppml)、颗类物(PM)浓度(mg/Nm3)和燃烧室上方温度(◦C)(注:文献中对该数据集无更为详细的描述).此处将28个样本的70%和30%分别作为建模数据和测试数据.

2) 实验结果.

首先,构建PLS模型,其全部8个LV的方差贡献率如表1所示.

如表1所示,全部LV提取的输入和输出数据累积方差贡献率为100%和77.08%,表明该文献选择的输入特征是合理的.

接着,计算输入特征的VIP值,如图4所示.

图4表明,全部8个特征的VIP值均大于1,其中第5个特征(CO浓度)具有最大值,其他特征按VIP值依次排序为第3个(烟道温度)、第1个(蒸汽负荷)、第7个(PM浓度)、第2个(烟气中H2O含量)、第4个(烟气流量)、第8个(燃烧室上方温度)、第6个(燃烧室上方温度).

表1 文献DXN 数据基于PLS 模型的方差贡献率统计表Table 1 Statistical table of variance contribution rate based on PLS model for ref DXN data

图4 文献DXN数据输入特征的VIP值Fig.4 VIP value of input feature for ref DXN data

采用遗传算法工具箱确定不同候选子模型的理想权重.同时,考虑到遗传算法存在的随机性,基于每个候选参数的候选子模型均运行20次进行均值统计.

最后,考虑ρFeSel和ρKLV是影响模型输入特征和集成子模型结构的关键参数,采用网格搜索法进行选择.结合图4可知,在取值为1,0.8,0.6,0.4和0.2时所选择的输入特征编号的子集分别为(5,3,1,7,2,4,8,6),(5,3,1,7,2,4),(5,3,1),(5,3)和5.设定ρKLV的范围为1～10,其最大值高于原始输入特征数量原因在于核技术扩展了变量维数.上述两个参数与模型预测性能间的关系如图5所示.

图5 文献DXN数据建模时ρFeSel和ρKLV与预测性能间的关系Fig.5 Relationship between ρFeSel and ρKLV and predicted performance for ref DXN data modeling

由图5可知:针对训练数据,ρFeSel=1时的平均预测误差稍弱于ρFeSel=0.8;但是针对测试数据,ρFeSel=1 且KLV=7 具有最佳平均和最小预测误差;针对训练和测试数据,选择较少输入特征建模时预测性能均具有较大跳跃性,这表明该算法针对小样本低维数据存在随机性.可见,适当选择ρFeSel和ρKLV的值是非常必要的.

3) 方法比较.

本文方法与文献,以及线性PLS基准方法等进行比较,结果如表2所示.

表2 文献DXN数据不同方法的预测误差比较结果Table 2 Comparison of prediction errors of different methods for ref DXN data

由表2可知:本文方法在ρFeSel=1和KLV=7时,具有最佳预测性能,其训练和测试数据的平均RMSE分别为23.79和78.30,较文献[12]的GP模型在精度上至少提高1倍多,较文献[13]的LS-SVM模型和PLS基准方法也有较大提高;此外,测试数据的预测范围波动比较大,但其最小平均预测误差值仅为70.98.上述结果表明,选择适当的输入特征和模型参数是非常关键的.

上述研究表明,本文方法是有效的.基于我国MSWI过程的DXN排放浓度数据构建软测量模型将更具有实际意义.

4.2 国内工业数据验证

1) 数据描述.

本文数据源于北京某MSWI焚烧企业,涵盖了2012-2018年测试的DXN排放浓度检测样本34组,其中:DXN取值为3次采样化验的均值,过程变量取值为采样当天24小时的均值(包含有效过程变量的数量为287);训练和测试样本等分,各为17组.

2) 实验结果.

首先,构建PLS模型,其前10个LV的方差贡献率如表3所示.

表3 国内DXN数据基于PLS模型的方差贡献率统计表Table 3 Statistical table of variance contribution rate based on PLS model for China DXN data

如表3所示,前10个LV所提取的输入和输出数据的方差累积贡献率为分别为90.25%和100%,表明较少LV能够蕴含建模数据中的多数变化.

接着,计算全部输入特征的VIP值,如图6所示.

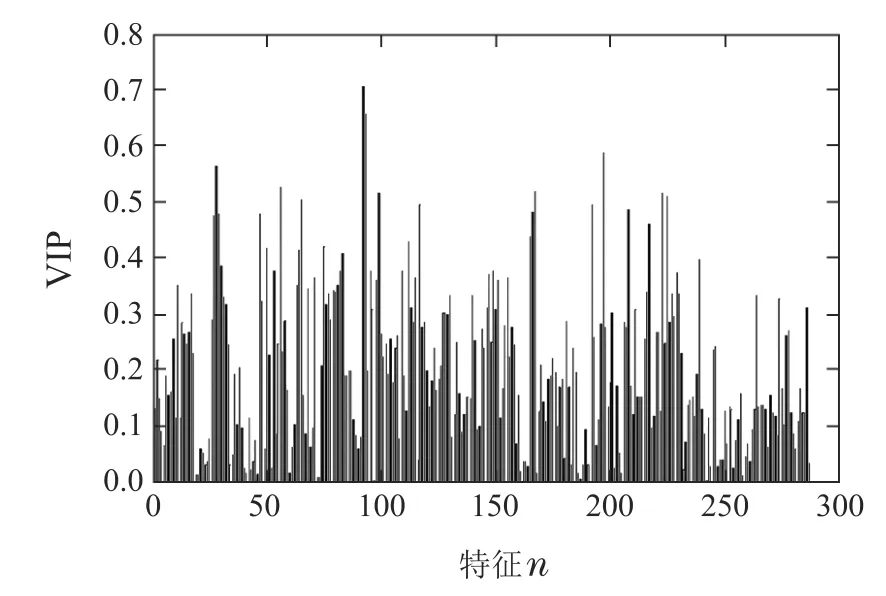
图6 国内DXN数据输入特征的VIP值Fig.6 VIP value of input feature for China DXN data

图6表明输入特征VIP值的最小值为0.9230e−4、均值为0.1999、最大值为0.7051,可见输入特征间具有较大差异性,其中排在前10的过程变量是:燃烬炉排左侧速度、燃烬炉排右侧速度、汽包炉水电导率、燃烧炉排右空气流量、炉墙左侧外温度、发电机前轴承振动、给水泵出口流量、烟囱排放CO浓度、给水泵出口给水压力、二次燃烧室左侧温度,取值范围为0.7051～0.5034;其中,除“汽包炉水电导率”和“汽包炉水电导率”外,均与DXN的生成、吸收和排放阶段直接相关,这表明了国内DXN数据的可用性,以及采用VIP选择输入特征的合理性.

图7 国内DXN数据建模时ρFeSel和ρKLV与预测性能间的关系Fig.7 Relationship between ρFeSel and ρKLV and predicted performance for China DXN data modeling

接着,采用与文献DXN数据相同的J和参数运行20次进行统计;取ρKLV=112;结合图6,设定ρFeSel的取值为0.01,0.03,0.05,0.08,0.1,其所对应的输入特征数量分别为2,8,14,22,28,采用网格寻优法获取ρFeSel和ρKLV值并分析其与模型预测性能间的关系.上述参数与模型预测性能间的关系如图7所示.

图8 国内DXN数据建模时核参数与预测性能间的关系Fig.8 VIP value of input feature for China DXN data

由图7可知:针对训练数据,在ρFeSel=0.1和KLV=9时具有最佳的平均预测性能;针对测试数据,ρFeSel=0.1和KLV=1时具有最佳预测性能,其中RMSE的均值为0.01792.核参数与模型预测性能间的关系如图8所示.

由图8可知,核参数的取值为300.因此,选择适当的输入特征和学习参数很必要.

3) 方法比较.

此处与基准线性PLS/核PLS方法进行比较,结果如表4所示.

由表4 可知:1)在选择28 个输入特征(ρFeSel=0.1)和KLV=1时,本文所提方法具有最佳预测性能,其最小RMSE为0.01643,其维数与原输入特征相比降低了近10倍,表明特征约简和SEN建模策略的有效性;2)采用线性PLS和核PLS建模时,在LV和KLV数量为1时具有最佳预测性能,其第1个KLV所提取的输入数据和输出数据的方差贡献率分别为56.76%和71.76%,比PLS 方法提高了20%～30%;但针对预测性能,却只是提升训练样本而未提升测试样本,这与特征约简的VIP值为线性和建模样本的数量稀少相关;3)所提方法的最小预测误差较核PLS方法在预测性能上具有较大提升,表明SEN策略是有效的.

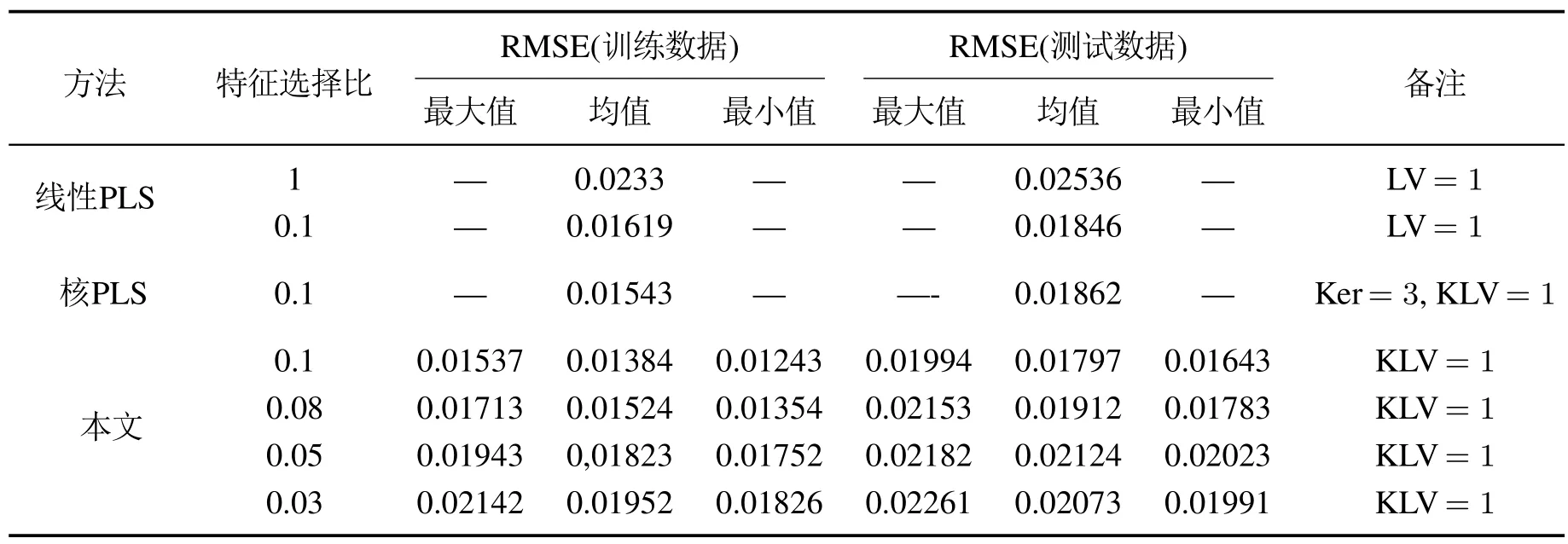
表4 国内DXN数据不同方法的预测误差比较结果Table 4 Comparison of prediction errors of different methods for China DXN data

综上可知,本文所提方法在如何进行非线性特征选择、如何同时优化特征约简与模型参数选择机制、如何降低模型的随机性等方面的研究还有待于深入进行.

5 结论

本文提出了一种新的基于特征约简和选择性集成算法的二噁英排放浓度软测量方法,其主要创新点是:基于线性潜结构映射模型获取的变量投影重要性以及依经验设定的特征约简比率因子确定输入特征;基于“训练样本重采样”的集成构造策略构建核参数自适应选择和模型复杂度依需求设定的选择性集成核潜结构映射模型.采用文献和国内的DXN排放浓度数据验证了所提方法的有效性.

进一步的研究包括:非线性特征选择、特征约简与模型参数优化机制、以及如何进行全阶段多相态二噁英浓度预测,以更好地为城市固废焚烧过程的运行控制提供支撑.