采用隔直参数分析不同PSS配置模型的适应性
刘翔宇,程 伦,李铁成,高泽明,何玉灵,陈二松,樊锐轶
(1.国网河北省电力有限公司电力科学研究院,河北 石家庄 050021;2.国网河北省电力有限公司,河北 石家庄 050000;3.华北电力大学 设备故障诊断与检测技术研究所,河北 保定 071003)
0 引 言
电力系统的动态稳定特性是关系到电网能否安全稳定运行的重要内容。为了改善电网规模不断增大和运行状况复杂化造成的不利影响[1-2],电力系统稳定器(PSS)被全世界广泛采用[3-4]。PSS被认为是最为经济、有效且原理清晰的增强电网动态稳定特性的措施[5],经过20世纪60年代以来的研究,已经发展出较为成熟的应用经验和配置方法。我国技术标准[6]中推荐的PSS参数配置方法为相位补偿法[7],但该方法对PSS配置过程进行了诸多等效,存在一定局限性,可能会对电网提供负阻尼[8]。随着电网运行状况的日益复杂化,优化和改善PSS配置技术对电网的安全运行具有重要意义。
目前针对提高PSS效果方面的研究,多从改善模型[9-13]和优化配置方法[14-17]的角度出发,也取得了一些成果。一些研究通过优化PSS模型改善其传函低频[9]和高频[10]的幅频特性,通过发展新的PSS-NB模型[11]、PSS4B模型[12-13]开辟PSS工程应用的新前景。另一些研究则将PSS配置过程转化为数学问题进行求解[14],希望通过优化算法得到更合适的参数[15-16],或通过优化相位补偿理论进行配置理论的改进[17],或考虑多机系统进行PSS参数的配置[18-21]。但这些研究多着眼于应用层面,而未回答如无补偿相频特性测量准确度[22]、开环补偿理论的适用性[23]、单机无穷大模型适用性等工程应用中的基础问题。
在基础问题方面,文献[22]提出了针对技术标准的改进建议,给出了工程应用中对无补偿相频特性的测量和处理方法,提出利用单机无穷大系统获得无补偿特性可能存在误差;文献[23]得到了开环补偿理论不能精确分析补偿效果,相频特性、幅频特性需要同时考虑的结论,并提出了隔直参数对PSS应用效果具有重要影响。但是现有技术标准并未阐述隔直环节参数的配置方法,现有研究文献也主要讨论移相环节参数的配置方法,隔直环节参数的配置缺乏有效的理论依据。另外实际电网的运行变化对系统的动态特性是具有明显影响的[24],对PSS的配置效果进行分析时,将系统等效为单机无穷大系统是否合理也需要进一步检验。
本文将在文献[22-23]的基础上,进一步研究和讨论PSS工程配置的一些基础问题,分析PSS隔直参数的配置方法。通过单机无穷大模型、双机模型、实际电网模型的对比,分析单机无穷大模型的适用性,给出工程配置PSS时的模型选取原则。另一方面,通过测试和分析研究隔直参数的配置方法,为工程上对PSS隔直环节的配置提供经验和依据。
1 加速功率型PSS模型
1.1 加速功率信号的获得
应用加速功率信号的优点在于可以消除“无功反调”问题。常用的加速功率型PSS模型如图1所示,该型PSS通过功率和转速信号的合成,形成加速功率信号ΔPa。加速功率信号的形成,首先需要对转速和功率进行测量,其次分别对测量得到的信号进行隔直处理,然后将两个信号进行合成得到ΔPm,最后合成信号经过滤波处理后,与功率信号测量值进行合成形成加速功率信号ΔPa。

图1 加速功率型PSS模型
1.2 隔直环节信号的合成分析
图1中转速隔直环节和功率隔直环节存在结构差异,这是由于两种不同属性的信号在直接合成前需要进行转化造成的。
采用标幺值表示的理想发电机转子加速转矩为
(1)
式中:ΔM为转子不平衡转矩;J表示转子的转动惯量;Pm表示原动机机械功率;Pe表示电磁功率;ω为转子旋转角速度。将式(1)写成偏差形式,加速功率为
(2)
式(2)可表示加速转速Δω和加速功率ΔPa之间的关系。以S表示微分计算,式(2)可进一步转换为
JSΔω=ΔPm-ΔPe=ΔPa
即
(3)
式(3)表示了加速功率与加速转速之间的转换关系,这也解释了图1中转速隔直环节和功率隔直环节为何存在结构差异。即功率信号需经过一个1/JS环节才能与转速信号进行合成。
1.3 PSS传函的相频特性
在功率振荡过程中,发电机的机械功率保持不变,此时ΔPm为0[25]。图1所示PSS模型可以简化为图2所示PSS模型。

图2 经简化的PSS模型
文献[23]已经给出了其相频特性的表达式,如式(4)所示。
φp=-arctan(ωTrp)-arctan(ωTw1)+π/2-
arctan(ωTw2)+arctan(ωT1)-arctan(ωT2)+
arctan(ωT3)-arctan(ωT4)
(4)
1.4 PSS工程配置的假设
PSS参数的工程配置[6]基于两个假设,一个是考虑PSS的补偿效果时应用开环补偿法进行计算分析可以等效于实际闭环系统[7];另一个假设是发电机连接无穷大系统,附加PSS逻辑结构前后不会对系统特性造成影响。如图3所示,也就是假设附加励磁环节(PSS)接入原系统前后,系统的特性不发生较大的变化。

图3 配置PSS采用的等效模型
实际上,任何对系统的更改均会造成整体系统特性的变化,这一假设是否具有普遍适用性尚需要进一步检验。
2 隔直参数影响的理论分析
选取实际电网中的某机组A作为研究对象,该机组额定功率为600 MW,采用自并励励磁系统,其励磁系统无补偿相频特性如图4所示,其主要PSS参数如表1所示。依据式(4)计算该机组的有补偿相频特性。当隔直参数Tw1、Tw2同步发生变化时,有补偿相频特性如图5所示。

图4 机组A的无补偿相频特性

表1 机组A的PSS工程参数

图5 机组A的有补偿相频特性
由图5可知,除了隔直参数为1时在0.1 Hz左右出现相位大于0°,理论上将出现负阻尼之外,其变化区间为[1,10]时,在0.1-2 Hz频段均提供正阻尼。图5中,随着隔直参数的增大,低频段相位补偿度增高,理论上隔直参数过高可能造成过补偿,且参数过大时隔直环节延时环节增加,会导致电压调节速度变慢和低频信号不易通过[5]。
3 基于双机模型的隔直参数影响
为检验隔直环节参数改变对发电机阻尼效果的影响,采用2节所述的发电机作为研究对象建立双机系统进行仿真分析。如图6所示,双机系统中机组A为研究对象,机组B为理想发电机模型。改变机组A的PSS隔直环节参数,仿真该双机系统发生某既定故障F后的功率振荡情况。

图6 双机系统PSS参数测试模型
3.1 0.4 Hz振荡影响分析
设置机组A的PSS为退出状态,调整图6中发电机的转动惯量,使发生F故障后系统振荡功率频率约为0.4 Hz。此时机组B与机组A的转动惯量比约为70.6。PSS退出运行时功率振荡曲线如图7所示。将机组A的PSS设置为投入状态,并采用实际工程参数,仅调整其隔直环节参数的大小,仿真不同隔直参数下发生F故障后功率振荡情况。随着隔直参数变化振荡频率和阻尼比变化如图8所示。

图7 惯量比为70.6时功率振荡曲线

图8 惯量比为70.6时振荡模式变化
对图7所示功率振荡曲线进行Prony分析,得到PSS退出运行时振荡频率为0.402 5 Hz,阻尼比为0.056 0。由图8可知,隔直参数在[1,10]区间内逐渐增加时,振荡频率由0.312 9 Hz增加到0.365 5 Hz,振荡阻尼比由-0.226 2增加到0.192 4。考虑到PSS退出运行时功率振荡阻尼比为0.056,则可知隔直参数取值为[1,4]时,PSS起负阻尼作用,取值在[5,10]区间时,PSS起到正阻尼作用。
3.2 0.7 Hz振荡影响分析
设置机组A的PSS为退出状态,调整图6中发电机的转动惯量,使发生F故障后系统振荡功率频率约为0.7 Hz。此时机组B与机组A的转动惯量比约为40.4。PSS退出运行时功率振荡曲线如图9所示。将机组A的PSS设置为投入状态,并采用实际工程参数,仅调整其隔直环节参数的大小,仿真不同隔直参数下发生F故障后功率振荡情况。随着隔直参数变化振荡频率和阻尼比变化如图10所示。

图9 惯量比为40.4时功率振荡曲线

图10 惯量比为40.4时振荡模式变化
对图9所示功率振荡曲线进行Prony分析,得到PSS退出运行时振荡频率为0.691 2 Hz,阻尼比为0.081 4。由图10可知,隔直参数在[1,10]区间内逐渐增加时,振荡频率由0.437 6 Hz增加到0.990 8 Hz,阻尼比先增加后减小,在隔直参数为5时达到最大值0.526 6。考虑到PSS退出运行时功率振荡阻尼比为0.081 4,则可知隔直参数取值为1时,PSS起负阻尼作用,取值在[2,10]区间时,PSS起正阻尼作用。
3.3 1.2 Hz振荡影响分析
设置机组A的PSS为退出状态,调整图6中发电机转动惯量,使发生F故障后系统振荡频率约为1.2 Hz。此时机组B与机组A的转动惯量比约为23.8。PSS退出运行时功率振荡曲线如图11所示。将机组A的PSS设置为投入状态,并采用实际工程参数,仅调整其隔直环节参数的大小,仿真不同隔直参数下发生F故障后功率振荡情况。随着隔直参数变化振荡频率和阻尼比变化如图12所示。
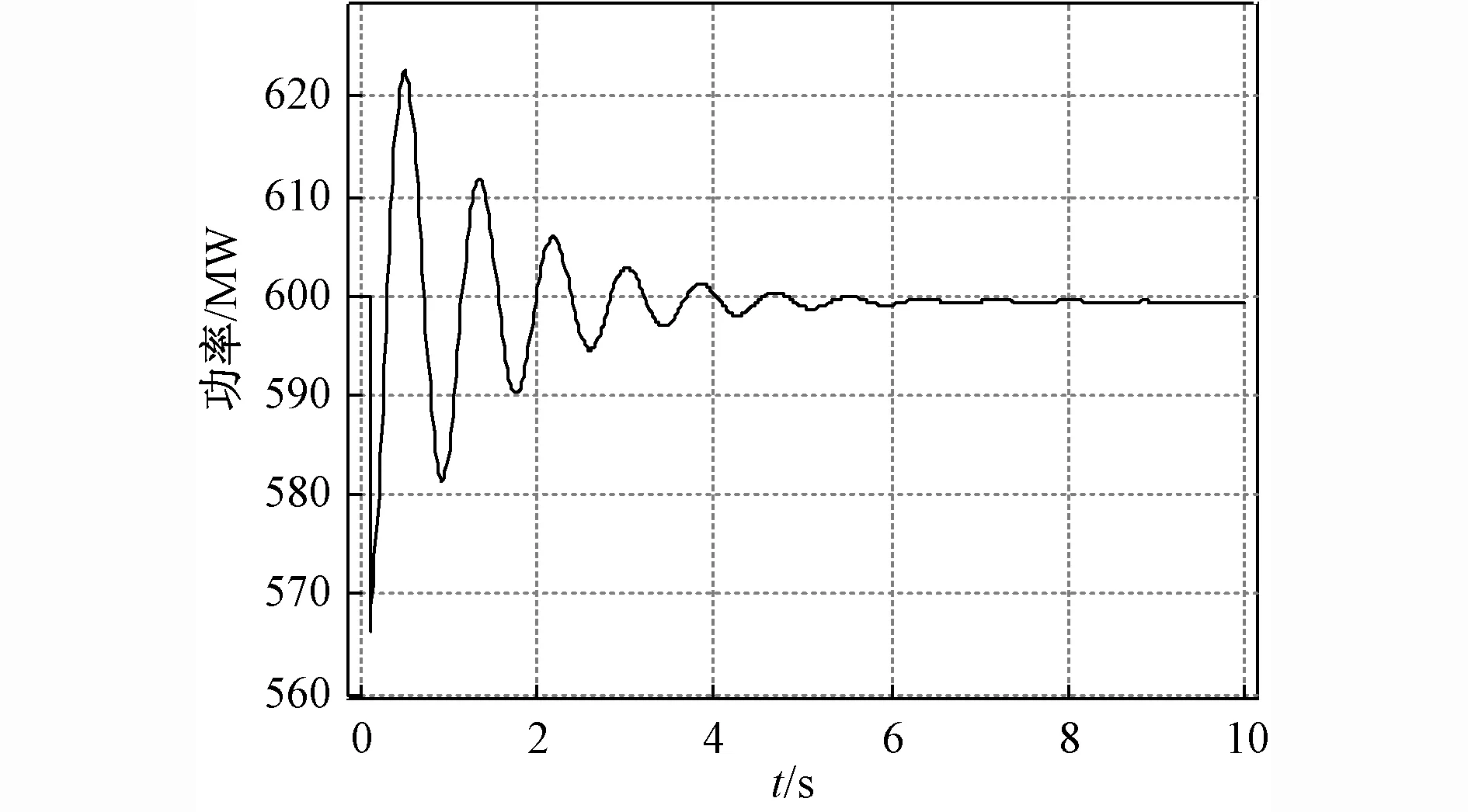
图11 惯量比为23.8时功率振荡曲线

图12 惯量比为23.8时振荡模式变化
对图11所示振荡曲线进行Prony分析,得到PSS退出运行时振荡频率为1.195 2 Hz,阻尼比为0.101 9。由图12可知,隔直参数在[1,10]区间内逐渐增加时,振荡频率先增长,后保持在1.4 Hz左右,且在[3,10]区间内变化较小;阻尼比先增加后降低,在隔直参数为2时达到最大值0.222 2。考虑到PSS退出时阻尼比为0.101 9,则可知隔直参数取值为[1,3]时,PSS起正阻尼作用,取值在[4,10]区间时,PSS起到负阻尼作用。
3.4 隔直参数影响的比较分析
由3.1-3.3节可知,采用不同隔直参数的PSS投入运行时,均会对双机系统原有振荡模式的频率和阻尼比产生影响。不同振荡模式下的频率和阻尼比影响如表2所示。

表2 隔直参数对频率和阻尼比影响
由表2可知,转动惯量比越大,系统原有的振荡频率越小。由于PSS的投入,发生相同故障时,系统的振荡频率发生了改变。在0.4 Hz的低频段,隔直参数取1时振荡频率最大变化了22.3%;在0.7 Hz的中频段,隔直参数取10时振荡频率最大变化了43.3%;在1.2 Hz的较高频段,隔直参数取1时振荡频率最大变化了53.4%。由此可知,PSS的投入对双机系统的动态特性造成了较大影响,隔直参数具有重要影响作用。
在PSS对阻尼比影响方面,0.4 Hz下增阻尼的隔直参数区间为[5,10],最优隔直参数为10;0.7 Hz下增阻尼的隔直参数区间为[2,10],最优隔直参数为5;1.2 Hz下增阻尼的隔直参数区间为[1,3],最优隔直参数为2。由此可知,隔直参数的取值不当,将造成PSS起负阻尼作用,不同的振荡频率下,隔直参数的最优取值不同。
另外,0.4 Hz振荡模型下,隔直参数为10时得到最优阻尼效果,此时振荡阻尼比变为0.365 5;0.7 Hz振荡模型下,隔直参数为5时得到最优阻尼效果,此时振荡阻尼比变为0.680 1;1.2 Hz振荡模型下,隔直参数为2时得到最优阻尼效果,此时振荡阻尼比变为1.269 3;三振荡模式下,阻尼效果最优的隔直参数,均为对原有振荡频率影响最小的隔直参数。
4 实际电网模型下的隔直参数影响分析
应用华北电网实际数据进行仿真分析,将机组A的PSS设置为退出状态,发生某故障后系统振荡功率振荡曲线如图13所示。将机组A的PSS设置为投入状态,PSS参数为工程参数,仅调整其隔直环节参数的大小,仿真不同隔直参数下发生相同故障后的功率振荡情况。振荡频率和阻尼比变化如图14所示。

图13 实际电网的功率振荡曲线

图14 实际电网的振荡模式变化
对图13所示振荡曲线进行Prony分析,得到振荡频率为1.231 3 Hz,阻尼比为0.076。由图14可知,隔直参数在[1,10]区间内逐渐增加时,频率由0.656 5 Hz增加到1.312 4 Hz,且在[3,10]区间内变化较小;阻尼比先增加后减小,在隔直参数为3时达到最大值0.333 2,此时振荡频率为0.843 3,相较PSS退出运行时变化31.5%。考虑到PSS退出运行时功率振荡阻尼比为0.076,则可知隔直参数取值在[2,8]区间时,PSS起正阻尼作用,其它区间起负阻尼作用。
5 不同模型的对比分析
5.1 单机无穷大模型的适应性分析
2节采用单机无穷大模型,进行理论分析得到的结论为,隔直参数在[1,10]取值范围内对0.1-2 Hz频段几乎均可起到正阻尼效果。3节采用双机模型仿真和4节实际电网仿真得到结果为,如隔直参数选取不当,将造成PSS提供负阻尼。三模型得到结论存在差异。
同时3节和4节仿真发现,PSS的投运会明显改变原有振荡频率,这一结果与单机无穷大模型的基本假设相违背。因此,采用单机无穷大系统进行PSS的配置分析是存在风险的。
5.2 双机系统与实际电网对比分析
对比3.3节与4节振荡模式,发现实际电网振荡模式与双机模型1.2 Hz振荡模式较为相近。PSS退出运行时两者的振荡频率均接近1.2 Hz,隔直环节参数对其振荡频率和阻尼比变化规律的影响也存在相似之处。这表明了采用双机模型进行仿真分析可以较为准确的反应PSS参数的配置效果及PSS投入运行对原系统特性的影响。因此可以一定程度上推定,如采用实际电网仿真时发生的振荡频率约为0.4 Hz和0.7 Hz,则其振荡特性应与3.1节、3.2节双机系统振荡模式较为相似。
另外,由于4节与3.3节振荡模式相似,则一定程度上可以认为4节实际电网模型下,等效转动惯量比应接近3.3节的23.8。由此可知,在实际电网中配置PSS参数时,采用单机无穷大模型(转动惯量比无穷大)是不够合理的。
6 结论及建议
本文通过单机无穷大理论系统分析、双机系统和实际电网仿真分析的方式分别研究了PSS隔直环节参数的适应性,以及隔直参数变化对功率振荡模式的影响。通过对三种方式得到结果的对比和分析得出主要结论和建议如下。
6.1 结 论
(1)隔直参数的配置对PSS阻尼效果具有重要影响,处于不同振荡模式发电机的最优隔直参数不同,其选取不当将可能使PSS对振荡提供负阻尼效果。
(2)在[1,10]隔直参数取值区间内,机组处于0.4 Hz左右低频振荡模式时,较大的隔直参数更利于提高阻尼;机组处于0.7 Hz左右的中频振荡模式时,适中的隔直参数更利于提高阻尼;在机组处于1.2 Hz左右的振荡模式时,较低的隔直参数更利于提高阻尼。
(3)PSS的投运将影响系统原有的功率振荡模式,隔直参数的变化既可能增大也可能减小原有振荡频率。
(4)采用单机无穷大模型分析PSS阻尼效果并不准确,可能造成分析结果与实际效果相差较大的情况,利用该模型分析问题存在潜在风险。
6.2 建 议
(1)隔直参数的确定应作为PSS参数整定的重要内容,并且其取值应结合实际电网中机组参与的振荡模式来确定。
(2)由于采用单机无穷大系统难以准确分析PSS的实际阻尼效果,本文推荐配置PSS参数时采用的研究模型优先顺序为,实际电网仿真、双机系统仿真、单机无穷大系统。

