探寻试题考查本质 聚焦数学核心素养——2019年高考全国Ⅱ卷理科数学第21题的探究

丁智辰

(甘肃省定西市教育局 743000)

一、考题呈现

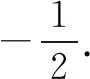
(1)求C的方程，并说明C是什么曲线；

(2)过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为点E，连接QE并延长交C于点G.

①证明：△PQG是直角三角形；

②求△PQG面积的最大值.

二、试题解答

本题的第(1)小题利用题设条件直接列出方程，通过化简得到曲线轨迹方程及轨迹，是解析几何轨迹求解中的常见问题，关键在于除掉杂点；第(2)小题主要考查利用直线与椭圆的位置关系，判断三角形形状以及求解三角形面积最大值问题，强化基础知识和运算求解的基本技能，考查推理论证、数形结合、函数综合应用的思想，立意深刻、内蕴厚重.2019年全国Ⅱ卷高考数学答案已给出本题的具体解答，本文不再赘述.

三、延伸拓展

高考解析几何试题年年岁岁题相似，岁岁年年意不同.该题作为高考数学压轴题，看似成规旧例，平淡无奇，但其蕴含着丰富的知识方法及深厚的试题背景，值得我们仔细研读，深度思考.我们应坚持以学生为本、落实新课标精神，引领学生发现问题、分析问题、解决问题，透过表面现象看其本质，加以引伸、拓宽、变化，引导学生从形式的“变”发现本质的“不变”，从本质的“不变”探索形式的“变”的规律，逐步提升学生的解析几何基本思想及数学核心素养.本题我们进一步将命题从特殊推广到一般，揭示事物的普遍规律，探本搠源.

1.问题拓展

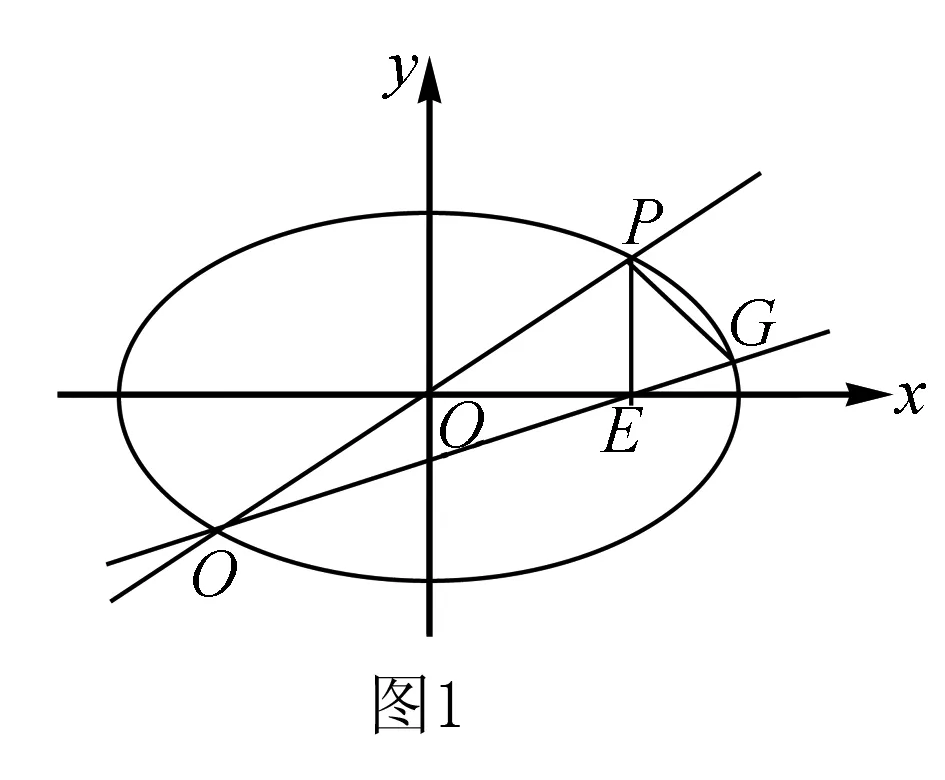
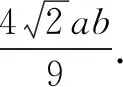
证明(1)设直线PQ的斜率为k，则其方程为y=kx(k>0).

(a2k2+4b2)x2-2ua2k2x+u2a2k2-4a2b2=0.

①

从而直线PG的斜率为

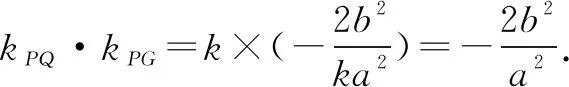
所以点G到直线PQ的距离

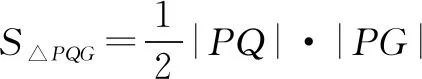
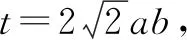
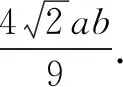
评注本结论探讨椭圆焦点在x轴上的情形，焦点在y轴上的情形可以自行探讨，结论仍然成立.

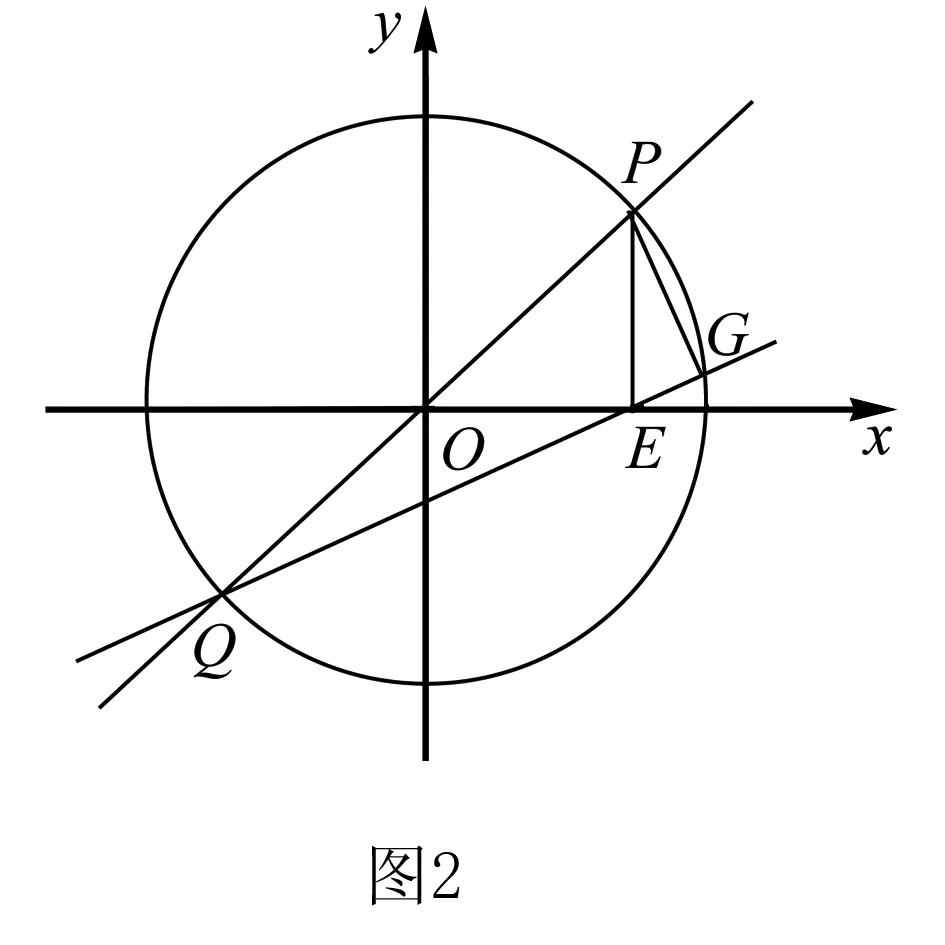
结论2 如图2，已知圆C的方程为x2+y2=r2，过坐标原点的直线交圆C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为点E，连接QE并延长交C于点G.

求证：(1)直线PQ，PG的斜率乘积等于-2；

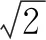
2.问题探究

由结论1和结论2可以看出，在封闭曲线圆和椭圆中具有kPQ·kPG为定值及△PQG面积存在最大值的结论.在教学中，我们将进一步探索在其他圆锥曲线中是否具有一定的结论.至此，我们可以联想到，问题在双曲线中是否成立？下面我们将在非封闭曲线双曲线中加以探究.

(2)△PQG的面积不存在最值.

证明(1)设直线PQ的斜率为k，则其方程为y=kx(k>0).

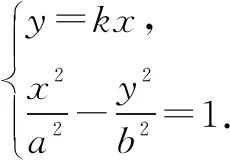
(a2k2-4b2)x2-2ua2k2x+u2a2k2+4a2b2=0.

③

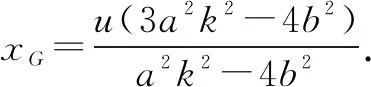
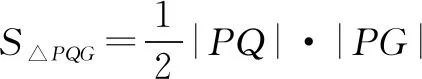
因此，当k趋近于0时，t趋近于+，则S趋近于0；当k趋近于时，t趋近于ab，则S趋近于+.

综上，△PQG面积的范围为(0,+)，即无最大最小值.

四、探究感悟

纵观近几年的高考解析几何试题，“依纲扣本”是命题的主方向，教材成为高考命题取之不尽，用之不竭的源泉.2019年高考全国Ⅱ卷理科数学第21题真正体现了高考试题“源于教材，高于教材”的命题理念，试题起点较低，容易入手，植根课本，注重创新，不落俗套，自然清新.第(1)小题完全与人教A版选修2-1第41页例3相同；第(2)小题在教材中多呈现直线与椭圆相交问题，特别是过焦点的直线与椭圆相交的相关问题，本题则涉及过坐标原点的直线与椭圆相交的三角形形状判别及三角形面积的最值求解问题，考生感觉似曾相识，又未曾见到过原题，对考生的思维是一种新的挑战，具有启迪思维，引导考生在探究活动中感悟数学，探究新知.

数学问题的探究，有助于学生体验数学研究的过程，有助于学生形成发现问题、探究问题的意识，有助于学生发挥自己的想象力和创造性.高考数学压轴试题很好地体现了数学基础、重视能力立意，引领中学数学回归课本，重视数学基本概念、基本方法.为了引导考生灵活应用解析几何的基本思想方法将问题合理转化，试题第(2)问进行了很好地设计，对考生的逻辑推理、直观想象等素养具有一定的要求.因此，试题不仅有利于高效选拔人才，也有利于中学数学教学的改革.

为此，在平时的教学中，通过问题的拓展探究，我们可以看到试题考查的实质所在，力促高考真题的引领活力，展现真题功能，挖掘真题潜能.从学生认知规律的角度，注重由浅及深，展开变式，引领学生在其思维水平的“最近发展区”探索，拾级而上，层层探究，真正做到“悟其必然，品其真味”，逐步落实数学核心素养，体现数学教学的核心所在.