极坐标下二维非线性薛定谔方程的有限差分方法
杨程程,张荣培
(沈阳师范大学 数学与系统科学学院,辽宁 沈阳 110034)
非线性薛定谔方程是量子力学中最重要的方程之一,在等离子物理、非线性光学、激光晶体中的自聚焦、晶体中热脉冲的传播以及在极低温度下的Bose-Einstein 凝聚体的动力学等领域内有着重要的应用[1-4]。
近年来,许多学者在求解非线性薛定谔方程时应用了许多数值方法,例如有限差分方法[5]、有限元法[6]、谱方法[7]和紧致积分因子法[8]等等。但这些方法均在直角坐标系下求解,而在极坐标下求解的非线性薛定谔方程的文章比较少[9],本文考虑在圆形区域上求解极坐标下的二维非线性薛定谔方程。
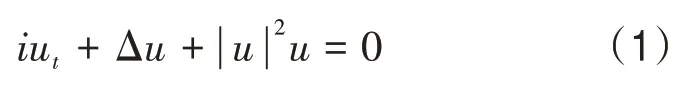
式中,u(x,y)为复函数;i2=-1 为虚数单位;Δu=uxx+uyy为拉普拉斯算子。
边界条件:在r方向的左边界为Neumann 边界;在r方向的右边界为齐次Dirichlet 边界;在θ方向为周期边界。

1 数值方法
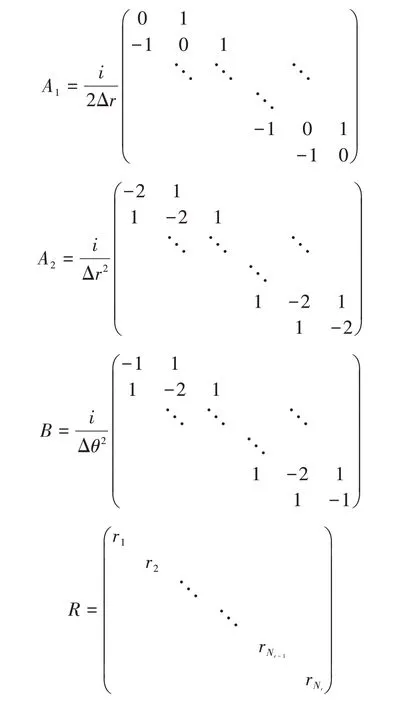
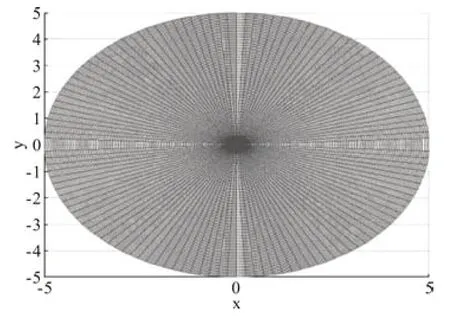
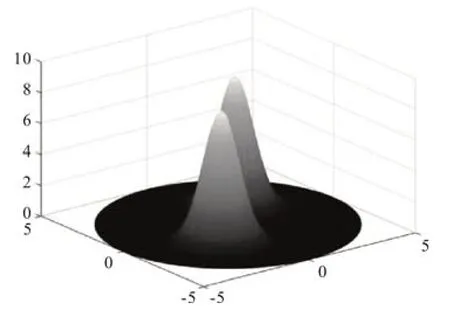
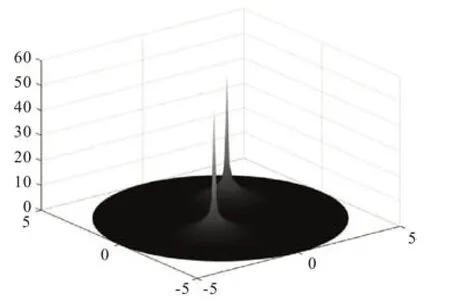
在式(1)中,将直角坐标系下的x与y转换为极坐标形式,即x=rcosθ,y=rsinθ。其中拉普拉斯算子可表示为Δu=urr+r-1ur+r-2uθθ。式(1)在极坐标下可改写为式中,0 图1 r方向的节点划分 根据泰勒展开式,式(3)中的导数可以离散为如下形式: 令u在网格节点(rj,θk)的数值解为uj,k,略去余项,得到式(3)的二阶中心差分格式: 由于式(1)在r方向的左端是齐次Neuman 边界,在r方向的右端是齐次Dirichlet 边界,在θ方向是周期边界,所以不存在边界的奇性。 为了能够用Kronecker积的形式来表示式(8),首先将式(8)写成矩阵的形式,然后再将矩阵的形式转化成Kronecker 积的形式。定义数值解uj,k的矩阵为 将非线性项写成向量的形式记为F。考虑到u在θ方向是以2π 为周期的,因此边界值为uNr+1,k=0,uj,0=根据式(8)、式(9)和式(10),可将非线性常微分方程式(11)写成如下紧致形式: 式中,矩阵的定义如下: 下面将式(12)向量化,将U和F按照列重新排成向量的形式,记U=vec(U),F(U)=vec(F),由Kronecker 积的性质(BT⊗A)vec(X)=vec(AXB)[10]可得 采用积分因子方法求解式(13),将时间区域剖分为tn=nΔt。其中,Δt为时间步长;n=1,2,…,N。令,式(13)写成 式(14)两边同乘积分因子e-Lt,然后从tn到tn+1求积分得 对式(15)应用梯形积分公式,得 式(16)中的指数矩阵与向量的乘积采用Kroylov 子空间的方法来求解。此方法的主要思想就是利用Kroylov子空间的元素来近似,其中具体实现方法参考文献[11]。由于积分的部分采用梯形求积公式进行离散,故精度为二阶精度。 不同时间下的计算结果以及爆破情况如图3、图4 和图5 所示。其中,图3 表示在t=0 时该方程的初始解,图4 表示在t=0.03 时的解,图5 表示在t=0.043 时的解。由图3、图4 和图5 可知,在t=0时有2 个环形解,且随着时间的增长,环形解的振幅逐渐增大,而环形解的半径逐渐减小,出现爆破现象,该结果与文献[6]的结果吻合。数值结果表明,本文提出的方法可以在圆形求解区域有效地捕捉爆破解。 图2 计算区域在r和θ方向上的网格 图3 t=0时该方程的初始解 图4 t=0.03时的解 图5 t=0.043时的解 本文对极坐标下的二维非线性薛定谔方程进行求解,将拉普拉斯算子在极坐标下表示,在空间上采用中心差分方法将离散后的式子用Kronecker积与矩阵向量化表示,最后采用积分因子方法进行求解。在实现过程中采用Kroylov子空间的方法来求解指数矩阵与向量的乘积,再利用不动点迭代方法在每个单元上求解非线性方程组。数值实验结果表明,采用Kronecker 积与矩阵向量化来求解在极坐标下的二维非线性薛定谔方程是有效的。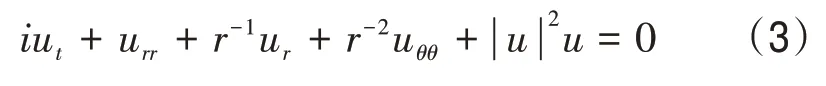
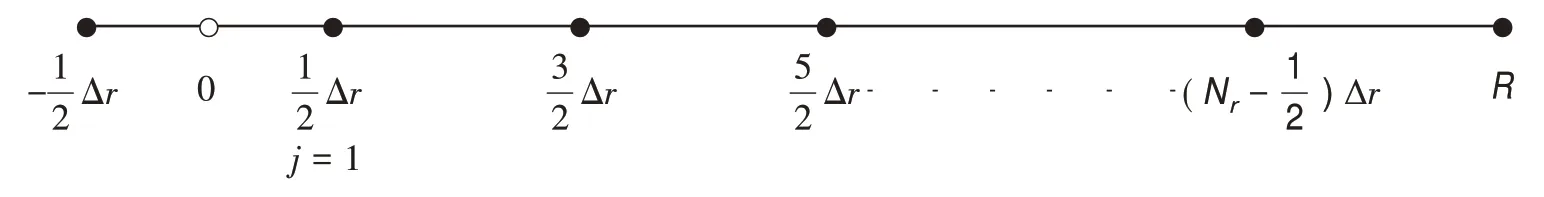
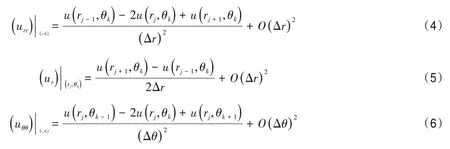

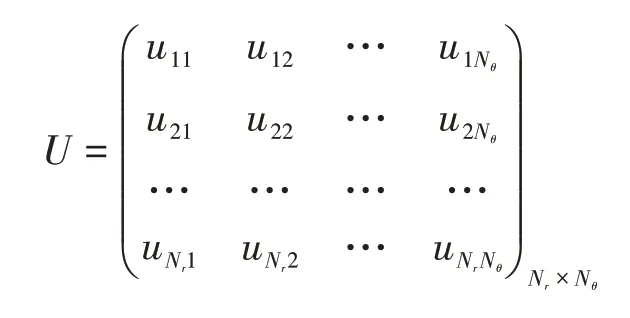
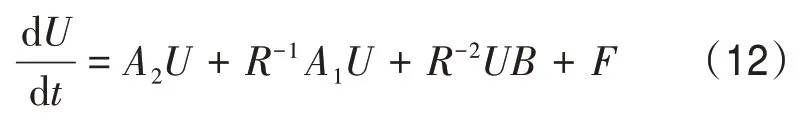
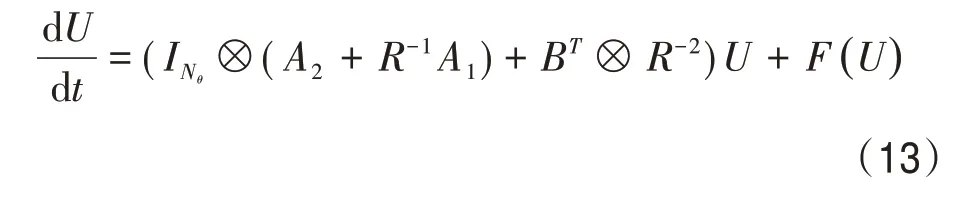
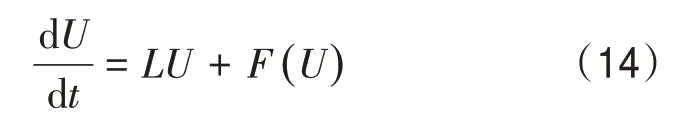
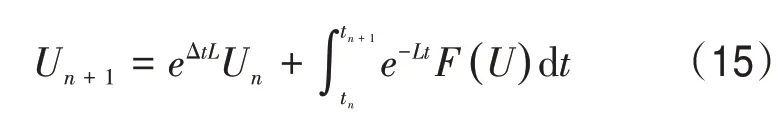
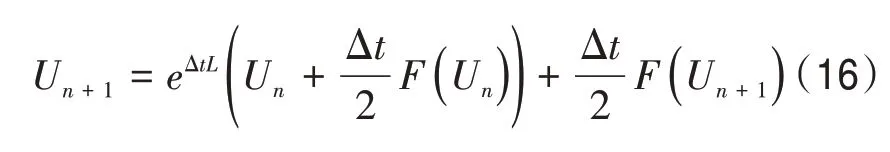
2 数值试验


3 结语

