基于卷积神经网络的多尺度融合特征图在人群密度估计中的应用
翁佳鑫, 仝明磊
(上海电力大学 电子与信息工程学院, 上海 200090)
人群密度作为人群的基本属性之一,反映了人群在空间中的拥挤程度。人群越拥挤,发生人员伤亡事故的可能性就越大,从而导致更大的人员伤亡和财产损失。对人群密度的实时监控可以及时发现异常状况,通知有关部门采取预防措施,以防止事故的发生。人群密度分布图可以直接反映人群密度的空间分布,连续的密度分布变化反映了人群行为的动态变化。聚集、奔跑、逃逸等异常行为经常导致人群的混乱和恐慌,增加事故的发生率,因此加强对异常行为的检测和报警,是降低事故风险的有效手段之一。
早期的人群密度估计相关研究大多是基于检测的方法,主要分为局部检测和整体检测[1]。其中,整体检测方式在对低密度人群的检测中表现非常出色,但在高密度条件下存在模糊阻挡等问题,检测性能下降。因此,研究人员通过使用基于特殊部位的检测技术[2]来解决这一问题,对特定的身体部位(包括肩膀和头部)使用增强分类器来估计该区域的人数。但该方法计算过程复杂,还需要训练一个能对图像全局扫描的多尺度检测器。另外,研究人员通过已知的图像输入和输出进行回归计数以获得更具鲁棒性和准确性的结果。回归计数由低级特征提取和回归建模两部分组成[3]。但是,这些技术着重于场景的整体属性。方向梯度直方图[4](Histogram of Oriented Gradient,HOG)是针对图像局部特征和纹理的检测技术,可进一步提高分类、检测和人群计数的准确性。完成局部和全局特征的提取后,可以采用线性回归、高斯回归、岭回归[5]和神经网络等方法来学习实际人群数与低层特征之间的映射。
近年来,深度学习在图像处理、模式识别及其他计算机视觉任务中获得了广泛的应用。使用深度学习的方法进行人群密度估计解决了规模、准确性、场景复杂性等问题,在视频监控中的应用日益成熟,能在突发情况时提供有效决策,保障人民群众的安全。文献[6]提出了一种具有多目标任务的可切换训练方法。文献[7]提出了一种多列卷积神经网络(Convolutional Neural Networks,CNN)人群计数技术,将几何自适应内核用于密度估计。每一列CNN中使用的卷积核大小不同,用于处理和计算不同范围内的人头数量,但最后的密度图聚合可能会降低预测密度图的质量。文献[8]首先通过一个网络将图像分为低、中、高密度3类,然后根据分类结果分别将图像传送到相应的3个CNN进行密度估计。但该方法没有联系浅层网络和深层网络,且引入的分类器增加了网络的复杂度。
针对上述问题,本文提出了一种以Unet++为基础的CNN,用并行连接的方式将浅层网络提取的细节信息和深层网络提取的高阶语义信息进行多尺度融合,以消除两者之间过大的语义鸿沟,并在网络前端引入膨胀卷积增大感受野,从而提高网络性能。
1 人群密度估计
通过CNN进行人群计数的方法通常分为两种:一是端到端的方式,即输入图像输出总人数;二是输出预测的人群密度图,通过求和的方式得到总人数。本文采用第2种方法,其优点是利用密度图提取头部信息,预测效率更高,且有助于适应人头尺度的多样性。
如果一个标注点的位置为xi,则该点的冲击函数可以表示为δ(x-xi)。因此,具有N个人头的标签可以表示为
(1)
但式(1)生成的密度图很稀疏,在网络计算损失时整体输出趋近于零,且不利于人群密度较大时的人数统计。因此,本文使用高斯函数对式(1)进行卷积,将标记为人头的位置变成该区域的密度函数,这样在一定程度上解决了图片的稀疏问题,又不改变图片中人数的计数方式。在真实场景下,特别是人群密度较大时,每个xi的位置并不是独立的。由于图片存在着透视失真现象,导致像素与周边样本在不同场景区域尺度下是不一致的,因此为了精确估计群体密度函数,需要考虑透视变换。

(2)

原始图像与基于几何自适应内核的方法生成的真值密度图如图1所示。将真值密度图的像素值求和,就可得到标记的总人数。

图1 原始图片和基于几何自适应内核的真值密度图
2 网络结构
2.1 网络模型
本文提出的网络模型如图2所示,此网络的特征提取模块(Conv1-1,Conv2-1,Conv3-1,Conv4-1)为VGG-16的前10层。
不同尺度的特征包含不同的信息,并且所有特征之间高度互补。例如,较深层的网络可以提取出高级语义信息,而在浅层网络中可以获得更多的低层细节信息。相关研究表明[9-10],这些互补特征可以相互完善。但使用加权平均和串联等简单的方法进行直接融合,无法很好地捕获这些互补信息,因此本文采用并行连接的方式进行重复的多尺度融合,以减小特征之间的语义鸿沟。

图2 网络模型示意
2.2 膨胀卷积
本文选择在Conv3-1和Conv4-1模块中引入膨胀卷积,在增大感受野的同时减少信息丢失。叠加卷积的膨胀率不能有大于1的公约数,否则会出现网格效应[11],因此需要将膨胀率设计为1,2,5的锯齿状。日常生活中的人群图像存在不同程度的透视失真,在局部区域的人通常具有相似的比例,与之对应在密度图上头部的半径相对均匀,但靠近摄像头的区域和远离摄像头的区域内人头半径差距较大。因此,将膨胀率设计成锯齿状,可以较好地实现同时捕获,即膨胀率小的卷积网络捕获靠近摄像头区域的信息,膨胀率大的网络捕获远离摄像头区域的信息。卷积核为3×3,不同膨胀率的膨胀卷积如图3所示。图3(a)对应膨胀率为1的膨胀卷积,与普通的卷积操作相同,感受野为3。图3(b)是膨胀率为2的膨胀卷积,只有灰色的点和3×3的核发生卷积操作,则感受野为(3-1)+(2×2+1)=7。图3(c)是膨胀率为5的膨胀卷积,叠加在膨胀率1和2的膨胀卷积的后面,能达到(7-1)+(2×5+1)=17的感受野。对比传统的卷积操作,3层3×3的卷积叠加起来,步长为1的情况,只能达到(核-1)×层数+1=7的感受野,与层数成线性关系,而膨胀卷积的感受野随着卷积核的增大呈指数级增长。
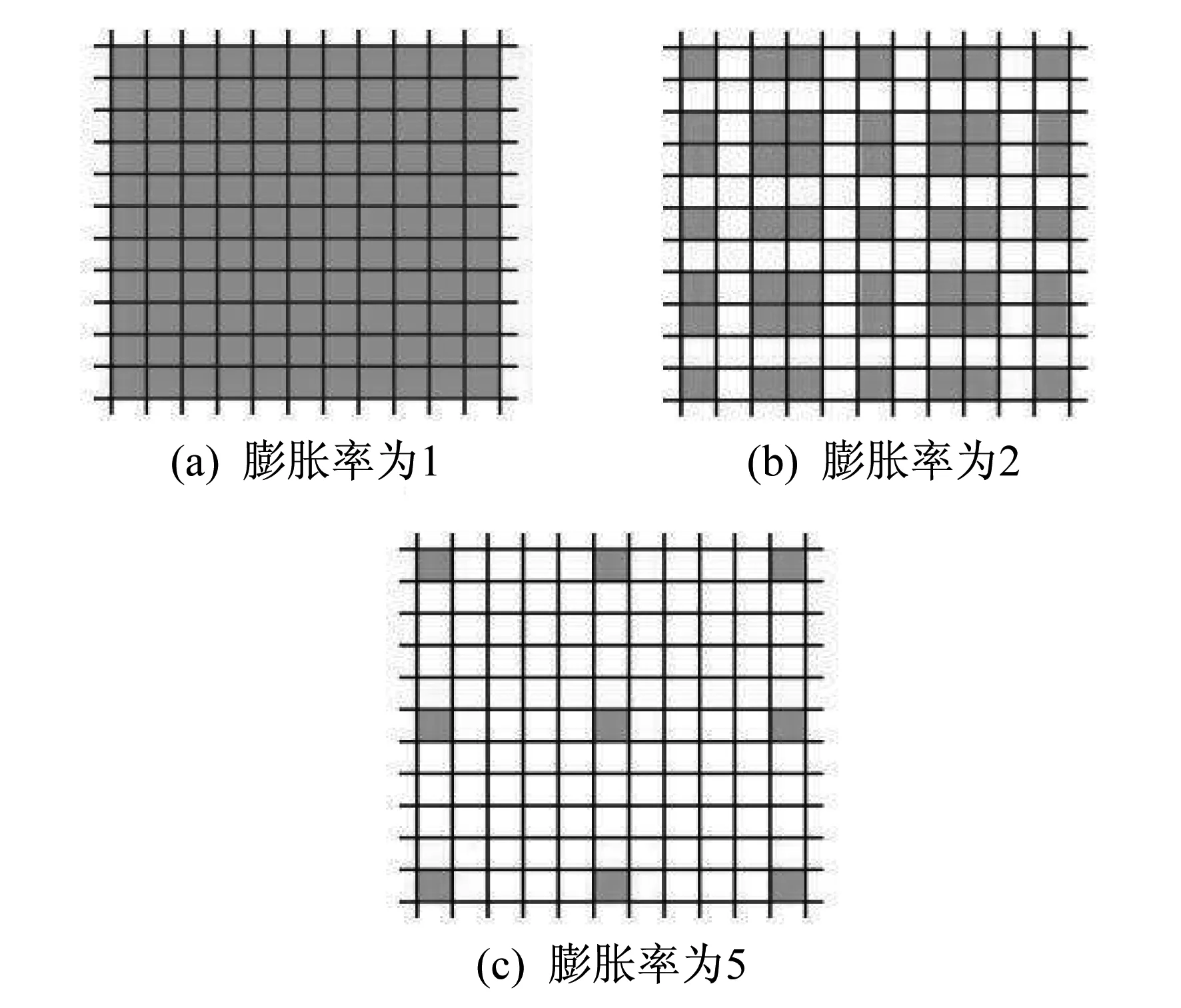
图3 不同膨胀率的膨胀卷积
3 实 验
3.1 实验环境
实验设备为配置TITAN XPascal的Ubuntu16.04系统,16 G内存。深度学习网络框架为Keras,后端使用的是Tensorflow,选择Adam优化器有助于网络更好地收敛,具体参数如表1所示。

表1 训练网络具体参数
其中,每个最大值池化核为2×2,每个卷积核为3×3,选择修正线性单元(Rectified Linear Units,ReLU)作为每个卷积后的激活函数。
3.2 评价指标
选用平均绝对误差(Mean Absolute Error,MAE)和均方误差(Mean Square Error,MSE)作为评价指标。MAE可以反映算法的准确性,MSE则反映算法的鲁棒性,其定义分别为
(3)
(4)
式中:M——测试集图片总数量;
Q(i)——测试集的预测人数;
P(i)——测试集标记的真实人数。
3.3 损失函数
利用欧氏距离对预测密度图和真值密度图进行比较,损失函数定义为
(5)
式中:Le——人群密度估计任务的损失;
S——一个训练批次中图像的数目;
G(Xi,θ)——第i张训练样本Xi的估测密度值,参数为θ;

3.4 数据集
本文在公开可用数据集Shanghai Tech和UCF_CC_50上进行实验。数据集参数如表2所示。

表2 数据集参数
3.5 实验结果分析
3.5.1 Shanghai Tech数据集
Shanghai Tech数据集共有1 198张标记图片,分为part A和part B两部分。part B部分的图片相较于part A部分的图片人群分布更为稀疏。本文选用300张part A部分的图片用于训练,182张用于测试;400张part B部分的图片用于训练,316张用于测试。
不同算法在Shanghai Tech数据集上的实验结果如表3所示。

表3 不同算法在Shanghai Tech数据集上的表现
从表3可以看出,与文献[13]相比,本文提出的网络模型在Part A部分MAE减小了15.3,MSE减小了17.9;在Part B部分MAE和MSE分别减小了4.8和4.7。这说明本文加入膨胀卷积,用并联的方式进行多尺度融合提高了网络的有效性。
3.5.2 UCF_CC_50数据集
UCF_CC_50数据集共有50张图片。该数据集虽然图片数量最少,但人群最为密集,且每张图片的人数变化大。本文选择与文献[3]相同的五折交叉方法进行实验,不同算法在UCF_CC_50数据集上的实验结果如表4所示。从表4可以看出,与其他算法对比,本文方法的MAE最小,表明本文提出的网络模型在人群密度较大的情况下也能得出较好的结果。
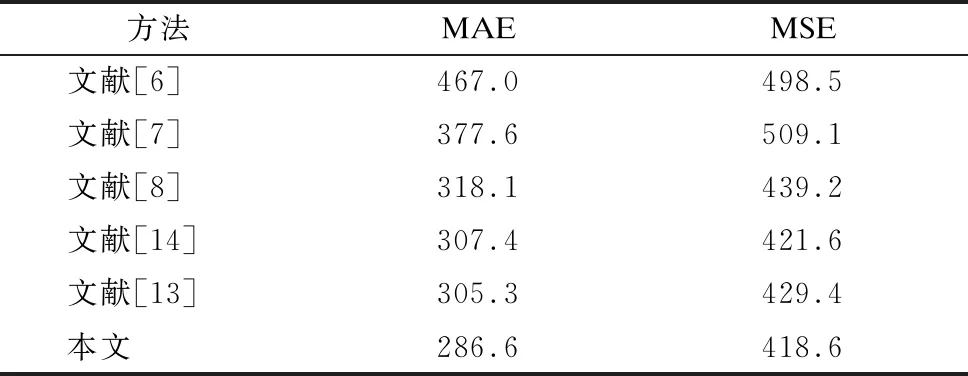
表4 不同实验在UCF_CC_50数据集上的实验结果
4 结 语
本文提出了一种以Unet为基础的卷积神经网络用于人群密度估计,用并行连接的方式结合由浅层网络提取的细节信息和由深层网络提取的高阶语义信息,然后进行多次多尺度融合,来消除两者之间过大的语义鸿沟。通过实验对比,本文提出的方法在公共数据集Shanghai Tech和UCF_CC_50数据集上均取得了较好的结果,验证了算法的可行性和有效性。

