桥梁监测中高频信号零漂修正技术的研究

皮欣裕，肖开喜，邓 箭，肖百朝，李富年，陈志丹

（1.武汉科技大学 信息科学与工程学院，湖北 武汉 430081；2.中建三局工程设计有限公司建筑设计院，湖北 武汉 430064；3.华中科技大学 土木工程与力学学院，湖北 武汉 430074）

0 引 言

近年来，桥梁安全事故不断发生，随着我国交通业快速发展，物流运输需求的不断增长，桥梁作为交通业中重要的环节，逐渐被人们重视起来。桥梁在使用的过程中，长期受到环境腐蚀、材料老化、人为因素等问题的影响，因此桥梁建设和使用的过程中需要对桥体各部位进行实时监测[1]，避免发生安全事故，造成不必要的损失。传统的桥梁监测是通过有线连接人工检查，需要大量的人力、物力、财力，桥梁维护效率低、实时性差。现代化的桥梁监测系统使用无线网络技术，传感器的安装方便快捷，克服了人工监测的缺点，桥梁维护效率高、实时性好，可以广泛运用于中小型桥梁监测。无线传感器网络是当前国内外研究的热点，有利于实现监测系统的小型化、智能化。目前我国的桥梁建设技术已经达到世界领先水平，随着大型桥梁的不断建成，如何做好桥梁的运营与维护，及时了解桥梁结构的健康状况已成为管理者迫切需要解决的课题[2]。本文以桥梁的振动监测为例，解决加速度传感器产生的零点漂移现象，以防数据在传输过程中出现丢包现象，采用光纤传输的方式，为后续桥梁项目提供可靠的监测数据。

1 加速度传感器的工作原理及零漂现象

1.1 加速度传感器的工作原理

加速度传感器种类有很多[3]，桥梁振动监测中常用的是压电式加速度传感器，利用压电效应原理，通过作用力造成传感器内部的压电晶体变形。根据牛顿第二定律，当被测物体振动频率远低于加速度传感器的固有频率时，力的变化值与加速度成正比。这种传感器体积小、灵敏度高、频率范围宽、成本低，但对温度特别敏感，容易产生零点漂移现象。

1.2 零点漂移产生的原因

传感器在数据采集中扮演着重要的角色。零点漂移是指传感器在输入信号为零时，受到温度的影响，导致输出端信号偏离原固定值上下浮动，当零漂信号偏差严重时会覆盖有效的数据。在桥梁监测系统中，振动监测的加速度传感器可分布在桥墩、桥塔以及桥身等地，长期的环境腐蚀导致传感器线路老化，容易出现零点漂移现象。

1.3 对比常用解决办法

常用抑制传感器出现零点漂移的方法有两种：硬件补偿法和软件补偿法。

硬件方面：材料的选择会影响零点漂移的程度，可通过使用对温度不敏感的材料，串并联恰当的热敏电阻减少温度带来的误差，这种补偿方法的优点是从根本上提高了测量的精确度，缺点是成本高、调试困难。文献[4-5]采用阻抗匹配的方式在硬件方面抑制传感器零点漂移现象的发生，实验结果验证了电路设计的可靠性。

软件方面：可使用Matlab 内置的系统函数detrend去除数据中的线性趋势，该方法不适用于非线性趋势项；可使用小波算法观察信号的基线趋势[6]，常用的小波函数有Haar 小波、Morlet 小波、Daubechies 小波，小波变换的方法建立在傅里叶变换的基础上，把信号区分为低频部分和高频部分：

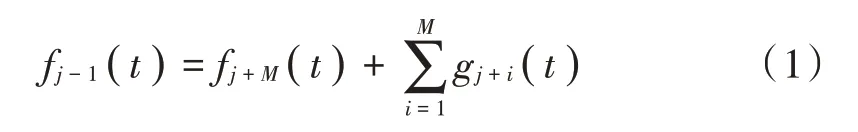
文献[7]利用bior 2.8 小波基函数成功消除了零点漂移，对实时数据进行处理，可使用数字形态学滤波方法降噪，以数字形态学理论中开闭运算为例：

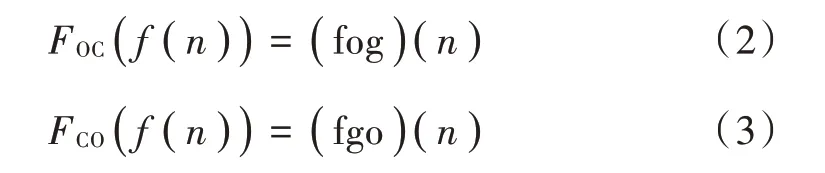
利用形态学基于形状的处理原理[8]，不考虑频带分布，开-闭和闭-开组合形态滤波器有效地去除非线性信号上的毛刺；可使用BP 神经网络降噪，BP 神经网络结构图如图1 所示，利用BP 神经网络设计出的补偿系统既可抵消温度对测试结果的影响，又起到信号压缩的效果[9]。

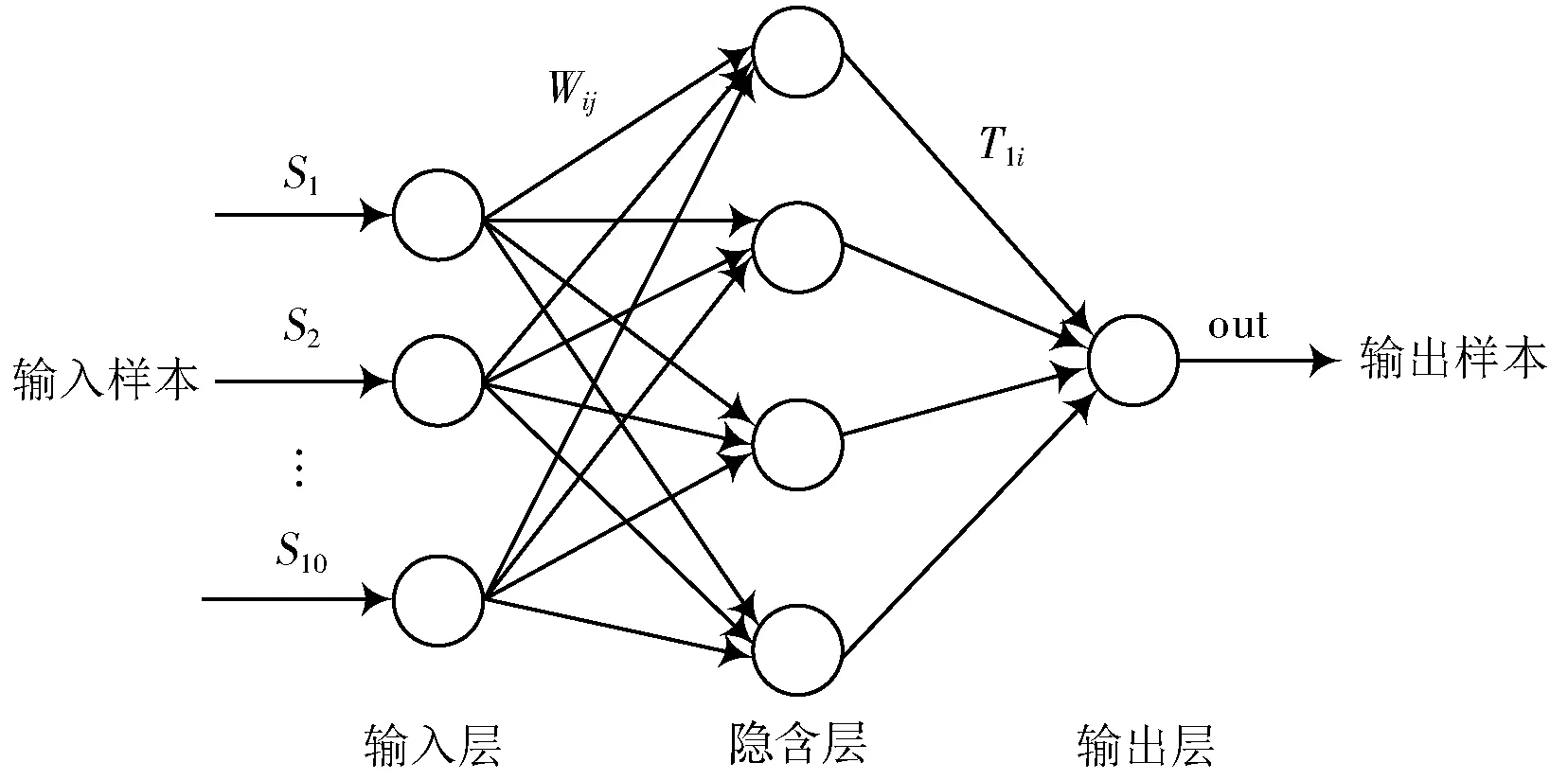
图1 BP 神经网络结构图

实际项目中，为了减少开发成本，通常选择使用软件方式修正数据。在桥梁监测系统中可采用小波变换、形态学滤波以及多项式拟合的方法处理零漂信号。根据各方法指标对比，多项式拟合算法简单且速度快，小波变换效果较好但运算量大，形态学滤波效果好但元素选取要求高，神经网络算法复杂。为了解决非线性趋势零漂信号的修正，本文提出使用多项式拟合的方法，然后将原始信号减去拟合信号得到去基线的信号[10]。多项式拟合的原理：对于给定的点使用式（4）进行n 阶多项式拟合：

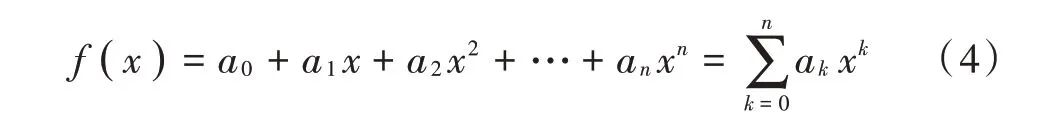
在程序执行过程中，多项式拟合去趋势所需时间为0.687 5 s，且可以快速检测出异常时间点，所以多项式拟合在工程中更有优势。

2 零漂检测与抑制算法实现

2.1 多项式拟合

多项式拟合流程图如图2 所示。

图2 多项式拟合流程图

实验伪代码如下：

2.2 数据采集

桥梁振动监测系统中，使用50 Hz 采样频率对振动传感器进行数据采样[11]，为了避免采集数据出现丢包现象，采集的数据通过光纤模块存储到数据库中。数据库中储存的字段包括采集时间以及每个传感器采集数据。Matlab仿真实验中调用FFT函数需要的数据个数为2n个，如有不足，通常做法是尾部补0，在处理零漂信号时采用补0操作会导致检测时间出现在补0位置，严重影响数据准确性。为了准确检测出零点漂移发生的时间，每次采样数据取出2n个，实验中数据采集以4 096个为例。

2.3 零漂信号检测

正常情况下，加速度传感器未出现零点漂移现象时，波形图不会出现异常数据点，数据平稳在一个均值附近没有偏移趋势，如图3 所示。

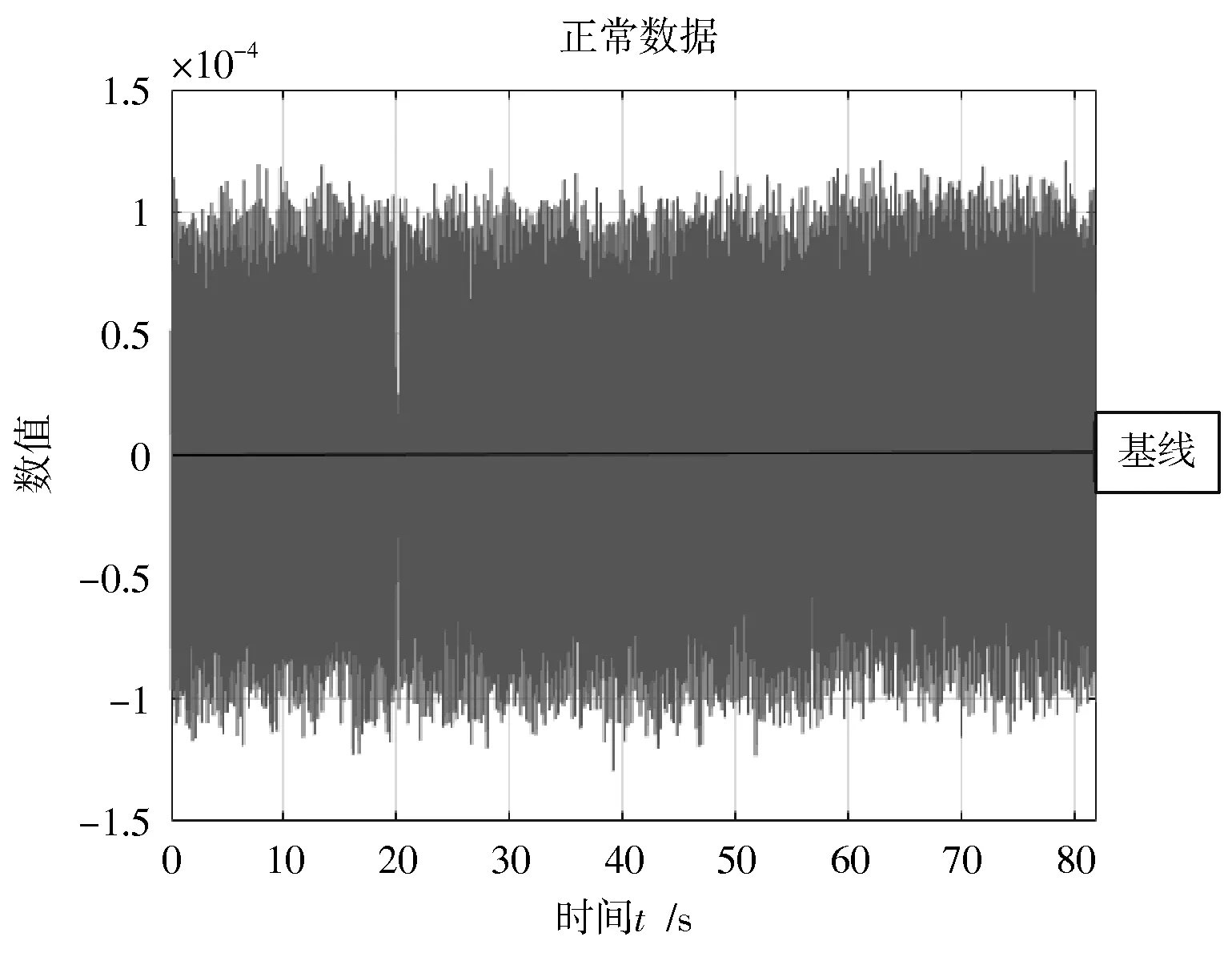
图3 正常数据的波形图

振动传感器数据采集出现零点漂移现象时，波形图出现异常突变数据点，有偏离原始均值的趋势，如图4所示。

为了检测出传感器发生零点漂移现象的时间，可使用加窗傅里叶变换，调用Matlab 中自带的spectrogram 函数来做短时傅里叶变换，可检测出在20.763 4 s 发生了零点漂移。

2.4 零漂信号抑制

为了提高加速度传感器的使用精度，检测出发生零点漂移的数据并且抑制误差数据的产生，需要使用多项式拟合算法进行降基线处理，通过拟合出的曲线推导出曲线的回归方程，对传感器产生的零点漂移误差进行补偿。如图5 所示，修正后的数据会在0 附近上下波动。

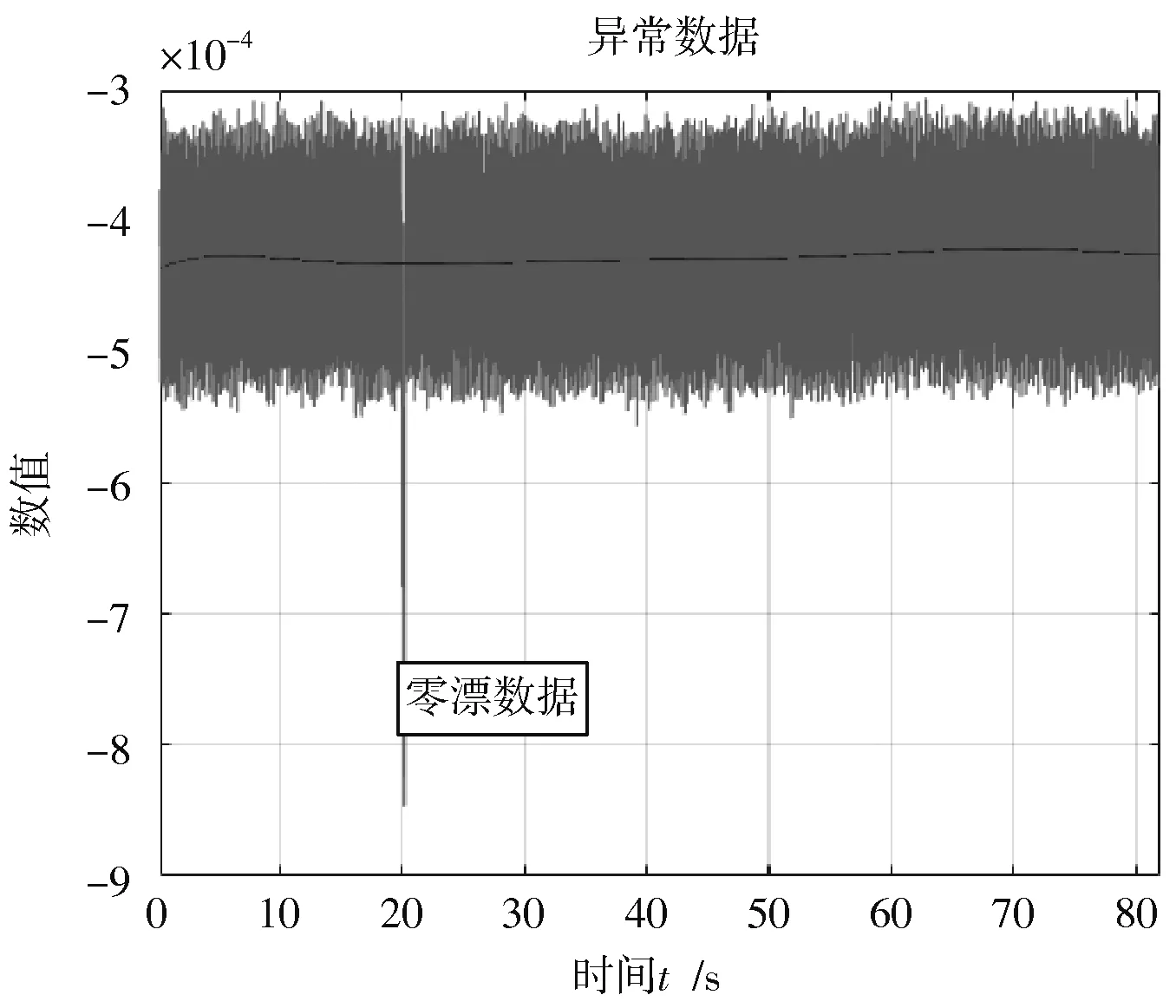
图4 零漂数据的波形图

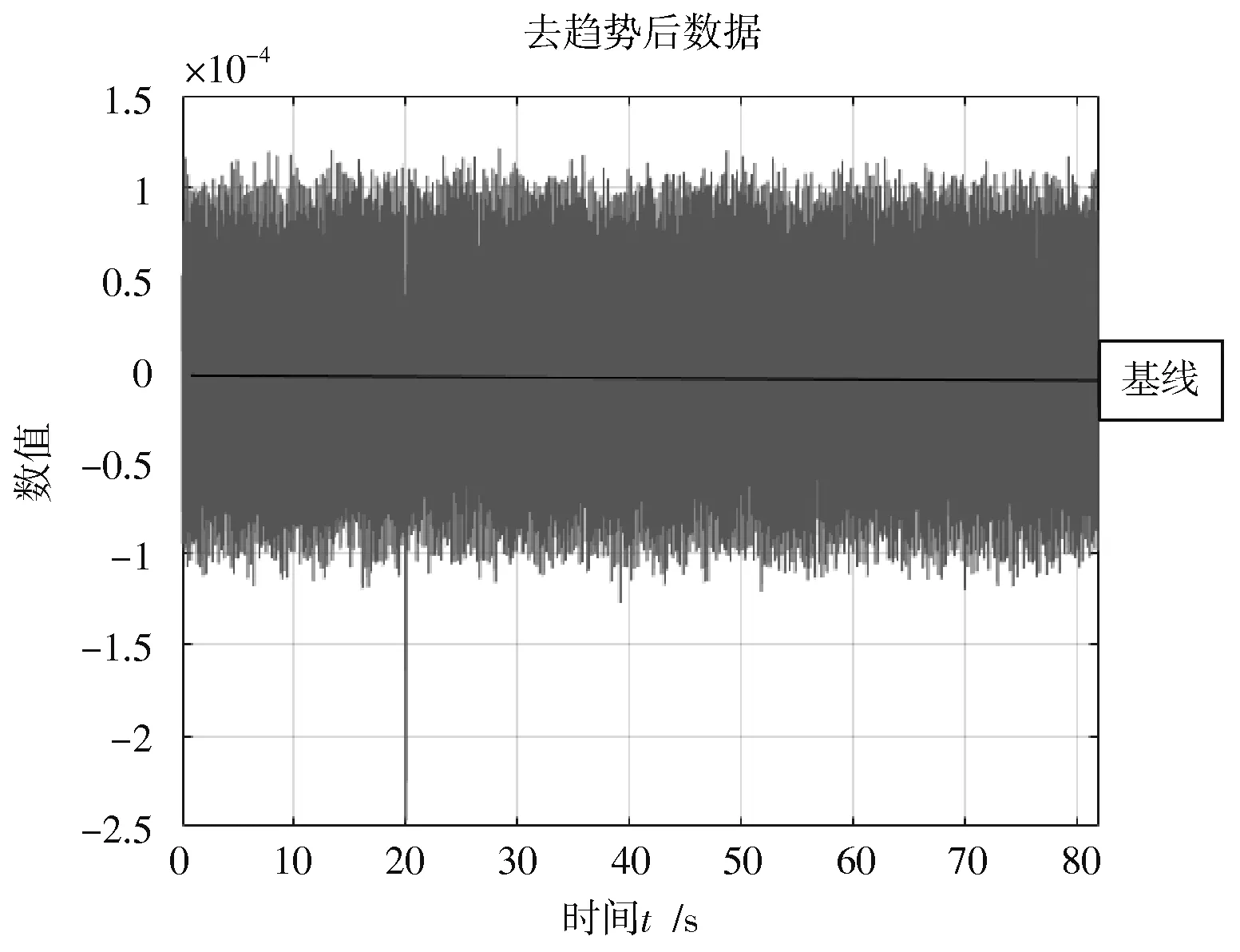
图5 修正后数据

3 实验结果及分析

在Matlab 中进行加速度传感器异常数据监测的仿真实验分析，其中采样频率设置成50 Hz，多项式拟合的阶数选择4，5，6，7 阶，分析不同阶数多项式拟合去趋势的效率和准确性，并且计算出发生零点漂移的时间点，如表1 所示，由此看来多项式拟合选取6 阶为宜。

表1 拟合阶数对比

综合对比4 种方法可得，小波变换方法抑制零漂信号，效果比多项式拟合好，但是小波变换运算量大导致程序运行时间过长。形态学滤波中元素的选取很重要，容易产生较大误差。对于BP 神经网络算法，更多的是对数据集的训练，学习出某种规则后才能最接近期望输出值，算法时间复杂度为O(n2)。方法对比如表2 所示，修正效果如图6 所示。最终选择使用多项式拟合方式对传感器零漂数据进行处理。

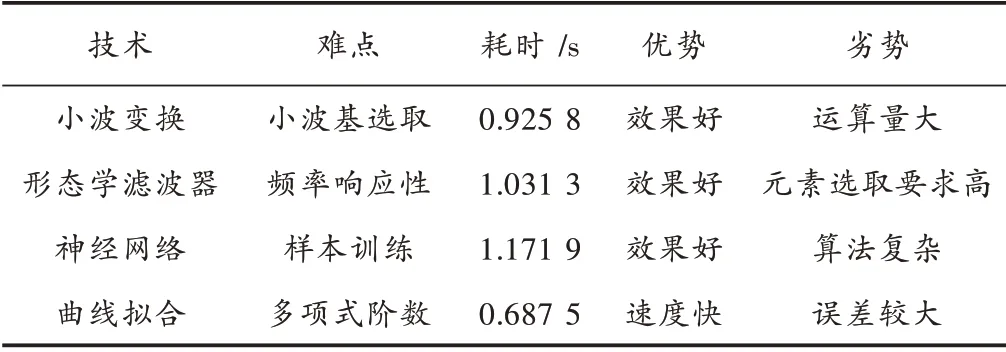
表2 四种降零漂方式对比

图6 四种方法降基线对比

4 零漂信号处理的工程应用

本文设计的多项式拟合处理零漂信号的方式已成功运用在赣江特大桥监测中。赣江特大桥是世界上第一个大跨度无碴轨道高速铁路斜拉桥，国内首座设计时速350 km 大跨度高速铁路斜拉桥，施工工艺复杂、监测技术难度大。工程中整个大桥上布置了11 个加速度传感器，采集的数据采用多项式拟合解决零漂信号，如图7 所示，虚线是零漂基线，曲线是降零漂过后的准确数据，图中1 是桥梁的侧面，2 是桥梁的断面。工程中多项式拟合数据处理效果好、速度快，符合项目所需。

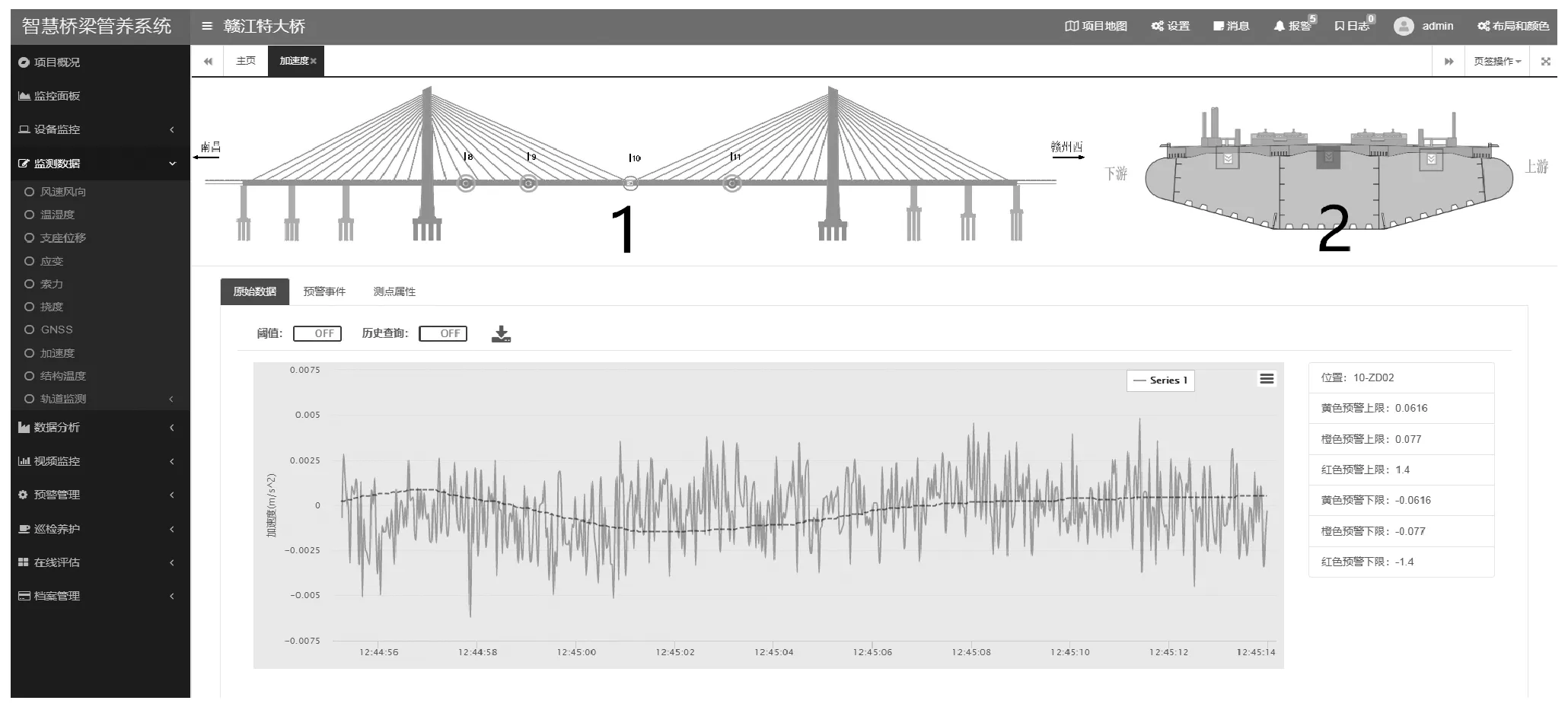
图7 赣江特大桥加速度零漂处理

5 结 语

本文主要讲述如何检测和抑制桥梁监测系统中传感器产生的零漂信号，对比了小波变换、形态学滤波、BP 神经网络和多项式拟合的优缺点，提出使用多项式拟合并用频谱分析的方案。实验通过对比分析不同阶数曲线拟合抑制信号消耗的时间，选取最合适的补偿算法，在赣江特大桥中为获取准确的桥梁监测数据提供了保障。

注：本文通讯作者为李富年。