插电式混合动力车油箱内置立柱结构优化研究

王帅，苏卫东，陈学宏 ，李志敏

(亚普汽车部件股份有限公司，江苏扬州 225009)

0 引言

随着世界经济的发展，能源危机与环境污染问题日益严重，为降低汽车排放，各大主机厂重点研究新能源汽车，在众多新能源汽车中，插电式混合动力汽车(Plug-in Hybrid Electric Vehicle，PHEV)既可以改善燃油经济性，也可以降低排放，与纯电动汽车相比具有充电时间短、行驶里程长、不依赖充电桩配套设备等优点，被认为是近期最有希望替代传统汽车的方案，广泛受到市场上消费者欢迎[1]。

PHEV汽车含有电池和燃油箱两套系统，当用户使用纯电模式时，发动机不会工作，燃油箱内部由于燃油晃动、周围环境温度变化等因素，使得燃油蒸汽挥发，造成燃油蒸汽逐渐增多，这将导致燃油蒸汽充满碳罐后溢出到大气中，不仅污染环境，还会导致碳罐性能下降[2-3]。为了降低碳罐的脱附次数，减少污染物的排放，需要将燃油蒸汽密封在燃油系统内。这就需要采用油箱隔离阀(Fuel Tank Isolation Valve，FTIV)将油箱内的高压气体隔离在油箱内，但这会导致油箱变形过大，因此内置立柱作为一种解决方案，可通过承受油箱内压载荷，减小油箱变形。本文作者首先对油箱内置立柱进行受力分析，随后运用Tosca优化软件中拓扑优化功能，优化立柱形状，使其体积最小的情况下，刚度最大化。

1 优化原理

传统结构设计，要求设计者经验丰富，工作繁琐，效率低，受到设计者经验限制，确定的方案往往不是最优方案，结构优化设计是将所有参与计算的量以变量形式出现，在满足规范和规定的前提下，形成全部可能的结构设计方案域，在众多可行的方案域中求解最优的方案。优化设计数学模型包括设计变量、目标函数和约束条件，最优化问题的一般表达式为[4]：

设计变量

X=[x1,x2,x3，…，xn]T

(1)

约束条件

(2)

目标函数

F(X)→max (或min)

(3)

在式(1)中，X为设计变量，即在优化设计中需要优化的变量，既可以是结构的形状参数，也可以是结构的材料属性，如弹性模量、泊松比等。结构优化设计便是寻求在给定约束条件下求设计变量的最优解问题。

式(2)为求解的约束条件，反映优化设计中应该遵循的规范要求。 约束条件一般分为约束方程和常量约束。约束方程指优化设计中根据结构刚度、强度以及模态频率等性能要求而建立的方程式，一般采用部分或者全部的设计变量为方程自变量，如式(2)中第一项所示。而常量约束则是指设计变量的取值范围，如式(2)中第二项显示。 常见的约束条件有几何约束条件、位移约束条件、应力应变约束条件和频率约束条件等。

式(3)是优化设计的目标函数，表示为优化设计中所要求的某些参数指标最大或最小。对于文中研究的燃油箱立柱结构优化而言，目标函数便是要求立柱结构的刚度最大。

2 仿真模型

为了获得油箱立柱最优结构，文中基本思路是建立简化油箱模型，进行内压分析获得油箱变形分布云图，随后按照基本布置原则，在最大变形位置附近布置两种类型立柱位置，一种H型立柱布置在油泵口附近，另一种I型立柱布置在其余位置，再进行内压分析，提取两种立柱受力情况，根据受力情况设置后续的拓扑优化载荷，最后定义设计变量、约束条件和优化目标来设置拓扑优化模型，获得拓扑优化结构后，再进行内压分析，验证结构的有效性，分析流程图如图1所示。

图1 结构拓扑优化流程图

油箱简化模型如图2所示，包括油箱本体、夹边和油泵口。油箱材料为多层高密度聚乙烯(HDPE)，厚度为5.5 mm，采用S3/S4壳体单元，夹边材料和单元类型与油箱一致，厚度为8 mm，泵口采用R3D3/R3D4刚体单元。夹边固定，油箱内部施加30 kPa压力，变形云图如图3所示，基本集中的中间部位，最大变形约41 mm。初步设计H型和I型立柱外形如图4所示，其中头部为了与油箱焊接，采用与油箱相同的材料HDPE，立柱本体为保证强度，采用PPA材料，参考变形云图，在变形最大位置附近共布置2个立柱，1个H型立柱和1个I型立柱，布置位置如图5所示，30 kPa内压仿真后，油箱变形云图如图6所示，最大变形12.75 mm，由此可见通过增加立柱，油箱的变形量降低约30 mm，效果明显。

图2 油箱简化模型

图3 油箱变形云图

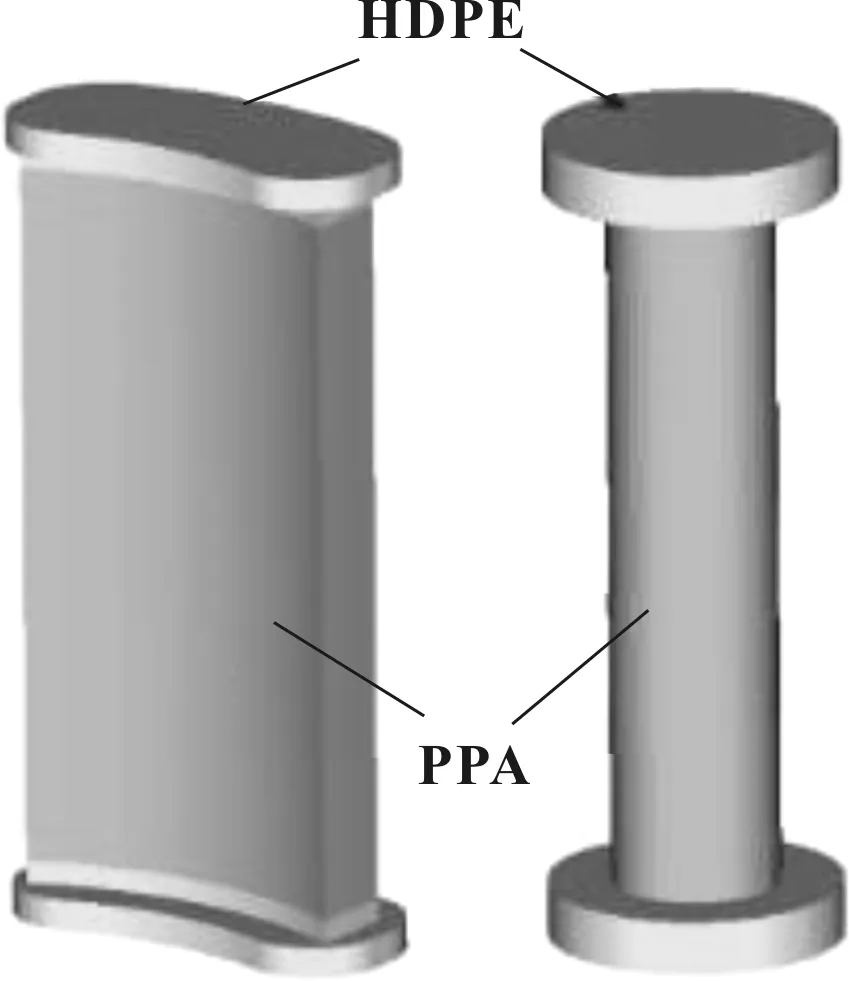
图4 H/I型立柱外形

图5 立柱布置位置

图6 立柱优化前油箱变形云图

由于立柱周围油箱刚度不同，变形不均匀，使得立柱受到正向拉力和弯矩载荷，在Abaqus中提取两种立柱受力情况，如图7所示，载荷大小见表1，从表中看出，H型立柱受力大于I型立柱，并且H型立柱受到弯矩力数值最大，H型立柱弯矩是拉力的17.5倍，I型立柱弯矩是拉力的5.2倍，后续拓扑优化载荷将以此为依据设置载荷大小。结合油箱结构分析，这是由于往往泵口处有较大平面，变形较大，另一侧有I型立柱支撑油箱，变形较小，整体呈现弯曲变形。

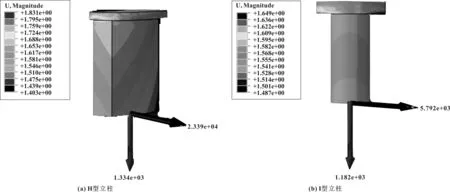
图7 两种类型立柱受力分析图

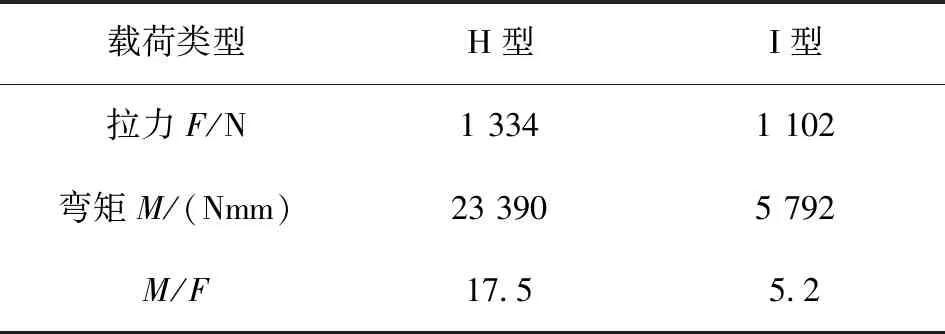
表1 两种立柱受力大小

3 立柱拓扑优化

拓扑优化是研究最大刚度下材料分布形式的问题，在实际工程问题中，拓扑优化一般都采用变密度法求解。变密度法是基于连续变量的密度函数来表达单元的相应密度与材料性能之间的对应关系，假定材料是由很多密度为0～1的单元组成，而弹性模量与密度之间则呈现指数关系[5-6]。文中定义设计变量为立柱设计区域的单元密度，冻结区域不进行优化，约束条件为立柱体积减小至少50%，优化目标为最小化应变能，即立柱刚度最大，两种立柱优化模型如图8所示。根据以上分析，设置立柱优化模型载荷，一端固定，另一端加载。对于H型立柱，Z方向拉伸载荷为1 N，X轴弯曲载荷为17.5 Nmm;对于I型立柱，Z方向拉伸载荷为1 N，X轴弯曲载荷为5.2 Nmm，如图9所示。

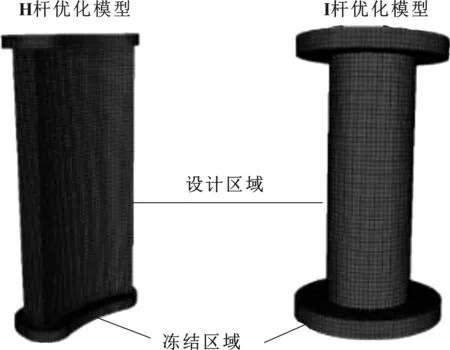
图8 立柱优化模型

图9 立柱优化载荷

优化的结构按不同载荷的传递路径保留了立柱体积，单独设置载荷的拓扑优化结果和混合载荷优化结果如图10所示，立柱的质量由0.75 kg降低到0.32 kg，减小了57.3%，采用优化后的立柱结构，再次进行30 kPa内压仿真验证，油箱变形云图分布与最大位置与优化前基本一致，如图11所示，最大变形大小为12.74 mm，与优化前立柱的油箱变形大小12.75 mm相近，说明优化结果的可靠。参考图10混合载荷的拓扑优化结果，结合具体使用要求，增加了孔和筋等结构，结构设计具体细节不在此赘述，设计的两种立柱结构实物，如图12所示。

图10 两种立柱在不同载荷下拓扑优化结果

图11 优化后油箱变形云图

图12 立柱实物图

4 结束语

由于油箱结构复杂多样，文中采用简化油箱模型(不含立柱)，通过内压分析得到油箱变形分布云图，基于此布置立柱位置，再次进行内压分析(包含立柱)，随后提取立柱受力情况，根据受力情况设置拓扑优化模型的载荷，最后定义设计变量、约束条件和优化目标来设置优化模型，分别得到H型和I型立柱沿Z轴拉伸载荷、沿X轴弯曲载荷及两种混合载荷的优化结果， 立柱的质量由0.75 kg降低到0.32 kg，减小了57.3%。优化结果为立柱设计提供了优化方向，具有理论指导意义。