进气系统空气流量计布置数值研究

于洋磊，胡见，曾志新，董愚

(广州汽车集团股份有限公司汽车工程研究院，广东广州 511434)

0 引言

作为汽车的重要组成部分，进气系统主要负责将净化后的空气输送进发动机燃烧室，气流的大小和稳定性将对发动机的动力性、经济性和整车排放等产生重要影响[1]。为此，在进气系统中一般安装有空气流量计，用于监测输送进发动机燃烧室内的空气量，以此作为ECU计算点火时间和喷油时间的重要依据，从而让发动机在各种工况下均可达到最佳的空燃比。为保证空气流量计测量的空气量具有准确性和代表性，对其布置的研究就变得极为重要。

CFD数值仿真是流体力学、数值分析和计算机结合的产物，是分析进气系统流场的主要方法[2]。在验证仿真模型及方法的基础上，利用STAR-CCM+软件，对不同插入角度、深度、轴向位置、管路入口圆角等因素影响下的空气流量计性能进行了系统研究，获得了各因素对空气流量计性能的影响规律，所得结论对空气流量计布置设计具有一定的指导意义。

1 模型建立

1.1 几何模型

图1是进气系统的三维数模，由进气管、空气滤清器、空气流量计、进气软管、进气硬管等组成。其中，空气流量计位于空气滤清器上壳体出口管路段。

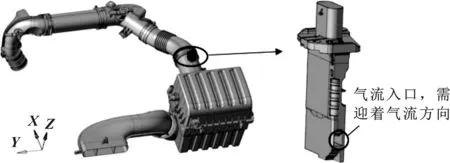
图1 进气系统数模

图2是不同布置位置下的空气流量计示意图。其中，图2(a)为不同插入角度的空气流量计位置示意图，以+Z方向为基准，在YZ平面内顺时针旋转角度α，得到不同插入角度的空气流量计布置；图2(b)为不同插入深度的空气流量计位置示意图，在YZ平面内，以空气滤清器上壳体出口管路段内表面最大Z坐标处为基准，向下插入深度h，得到不同插入深度的空气流量计布置；图2(c)为不同轴向距离的空气流量计位置示意图，为便于观察，以线框图进行展示。在XZ平面内，黑色空气流量计位置处于最左侧，以其气流入口为基准，向-X方向移动距离d，得到不同轴向距离的空气流量计布置；图2(d)为不同圆角半径的示意图，圆角位于空气滤清器上壳体出口处，其圆角半径为r。

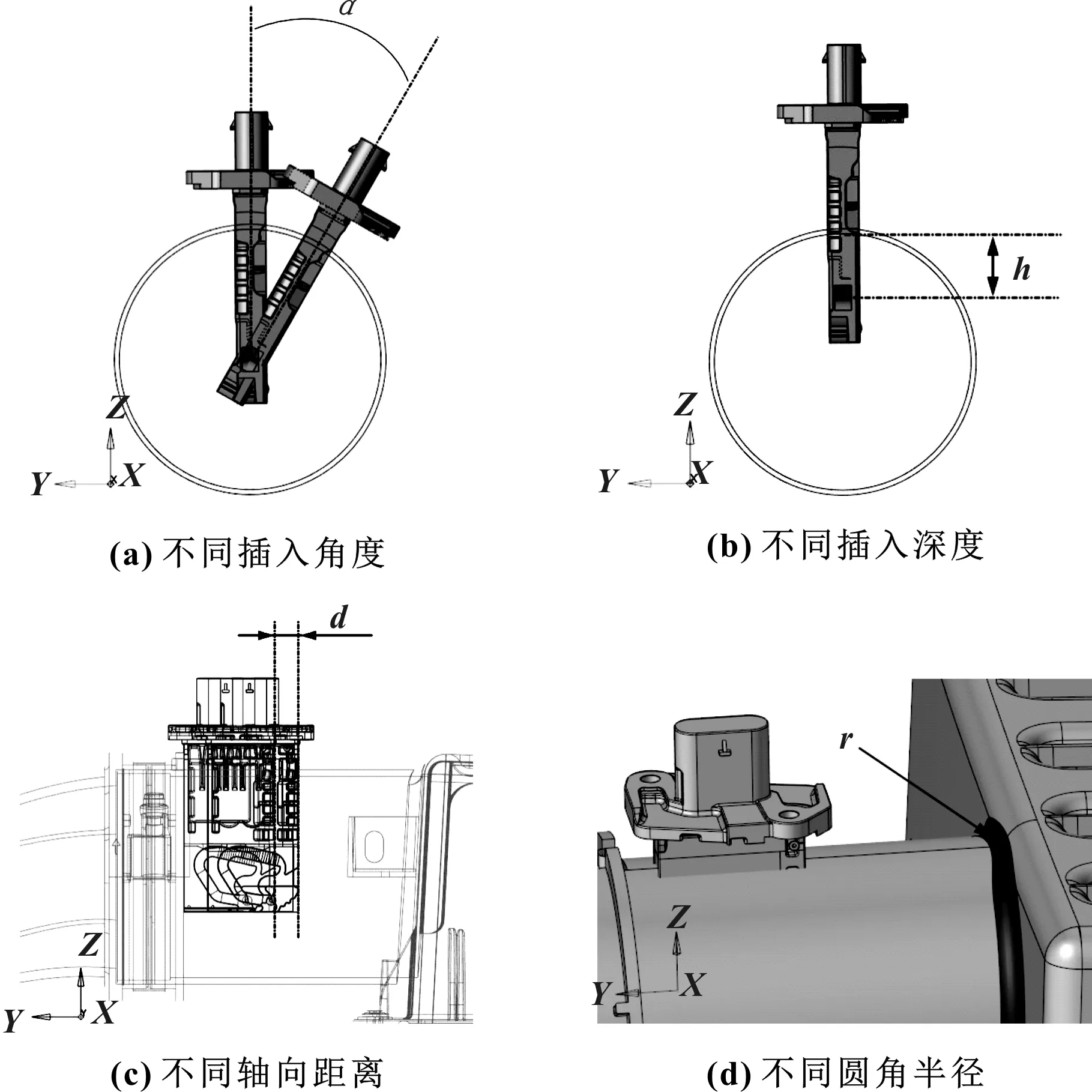
图2 不同布置位置的空气流量计示意

通过改变插入角度α、插入深度h、轴向距离d和圆角半径r等几何参数以及进气系统入口质量流量q，设计不同的物理模型来进行研究，变量参数设置范围见表1。

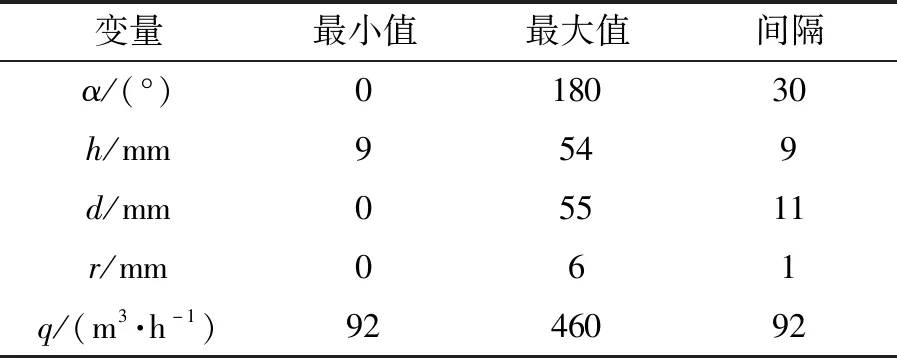
表1 变量参数范围

采用空气流量计入口速度偏差vd和湍流强度I对空气流量计布置性能进行评判。

(1)

(2)

式中:vmax为空气流量计入口最大速度，m/s；vmin为空气流量计入口最小速度，m/s；Re为雷诺数。

1.2 仿真模型

图3为进气系统流体域网格模型。在划分网格前首先进行几何处理，对模型进行适当简化，且为了考虑节流损失，在进气口建立半球形包络面，其半径为进气口水力直径的2倍。几何处理后进行面网格划分，经过网格无关性分析，采用网格平均尺寸为2 mm，局部物理梯度较大的地方缩小至0.5～1 mm，物理梯度变化平缓的采用3 mm尺寸网格。基于面网格，采用STAR-CCM+软件生成其特有的“蜂窝”状多面体网格，具有更多相邻单元，对于梯度计算和流动状况预测更准确，收敛速度更快[3]。对于近壁面区域，设置边界层，厚度为2 mm，为控制体网格数量，设置增长率为1.2。网格总数约为350万。

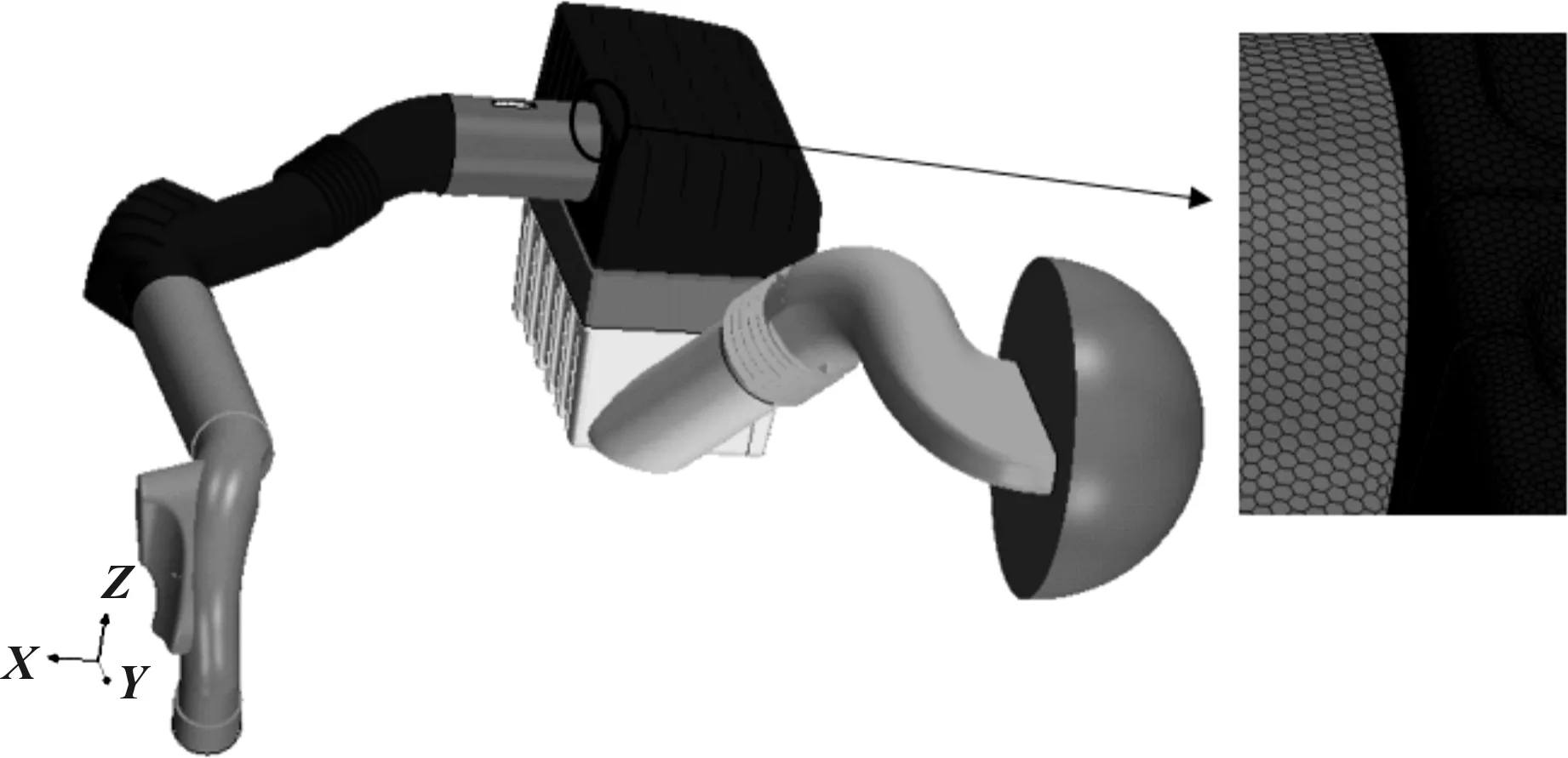
图3 网格模型示意

由于进气系统额定流量为460 m3/h，最大速度小于100 m/s，马赫数Ma<0.3，气体可被认为是不可压缩流体的湍流运动。湍流运动是一种非常复杂的非线性运动，如图4所示，其数值模拟分为直接数值模拟法和非直接数值模拟法两大类[4]。

图4 湍流数值模拟方法

直接数值模拟法(DNS)是指对流场的湍流运动不做任何形式上的简化，将流动域直接用瞬态的N-S方程进行求解。用此法进行计算可以得到比用非直接法计算更加精确的数值模拟结果[5]。但限于技术条件，还无法在计算机上直接进行计算。非直接数值模拟法是指先对湍流运动进行简化，再计算湍流脉动特性。依简化方法不同，其可分为Reynolds平均法、大涡模拟法以及统计平均法[6]。其中，标准k-ε模型目前被广泛应用于传热、燃烧以及发动机进气系统内的气体流动的计算等，是工程计算领域内应用最广的一种湍流模型[7]。

2 仿真方法验证

为验证仿真方法精度，在空滤器性能试验台上进行了不同入口流量下的进气系统压损试验。试验时环境介质参数见表2。

表2 环境介质参数

依据试验参数，进行相同条件下的数值仿真，入口条件设为压力边界，出口设为质量流量边界。进气系统视为绝热系统，壁面条件绝热、无滑移。

表3为仿真压损与试验压损的对比表，相对误差最大为5.05%，仿真方法具有较高的精度，该方法具有较高的可行性。

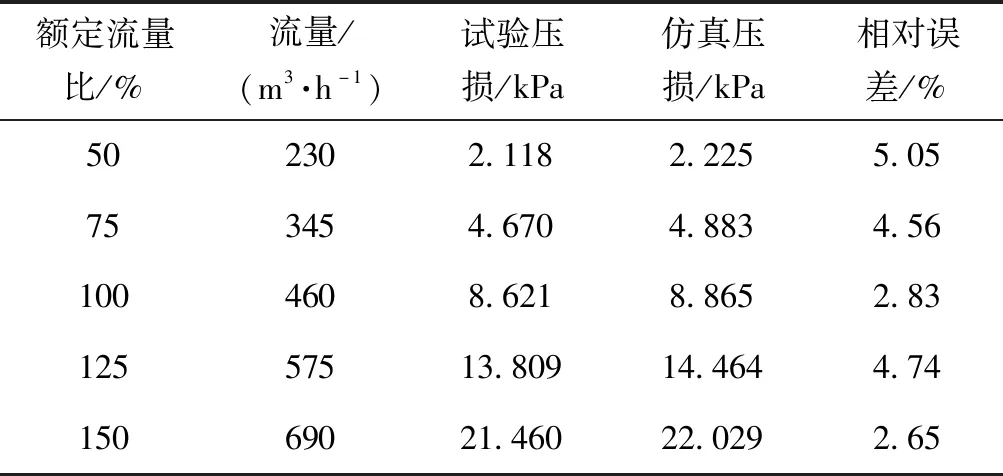
表3 仿真与试验结果对比

3 结果与分析

3.1 插入角度的影响

图5是不同插入角度的空气流量计在不同的进气系统流量时的入口速度偏差云图，X坐标为插入角度α，Y坐标为进气系统流量q，Z坐标为空气流量计入口速度偏差vd。在0°～30°区间，不同流量q下的速度偏差vd均随插入角度α的增大而大幅减小；在30°～60°区间，速度偏差vd减幅变小，且随着流量q的增大，减幅逐渐收窄，在额定流量460 m3/h时反而微增，最小值为35.58%；在60°～180°区间，对于低流量区，速度偏差vd随插入角度α增大而增大，最大值为48.93%，在中高流量区，速度偏差vd在120°～150°区间出现减小，且随流量q增大，减幅呈增大趋势。表明插入角度α对速度偏差vd影响明显，在高流量区，速度偏差vd相对更小，且存在最佳插入角度区间，使得不同流量下的速度偏差均较小。

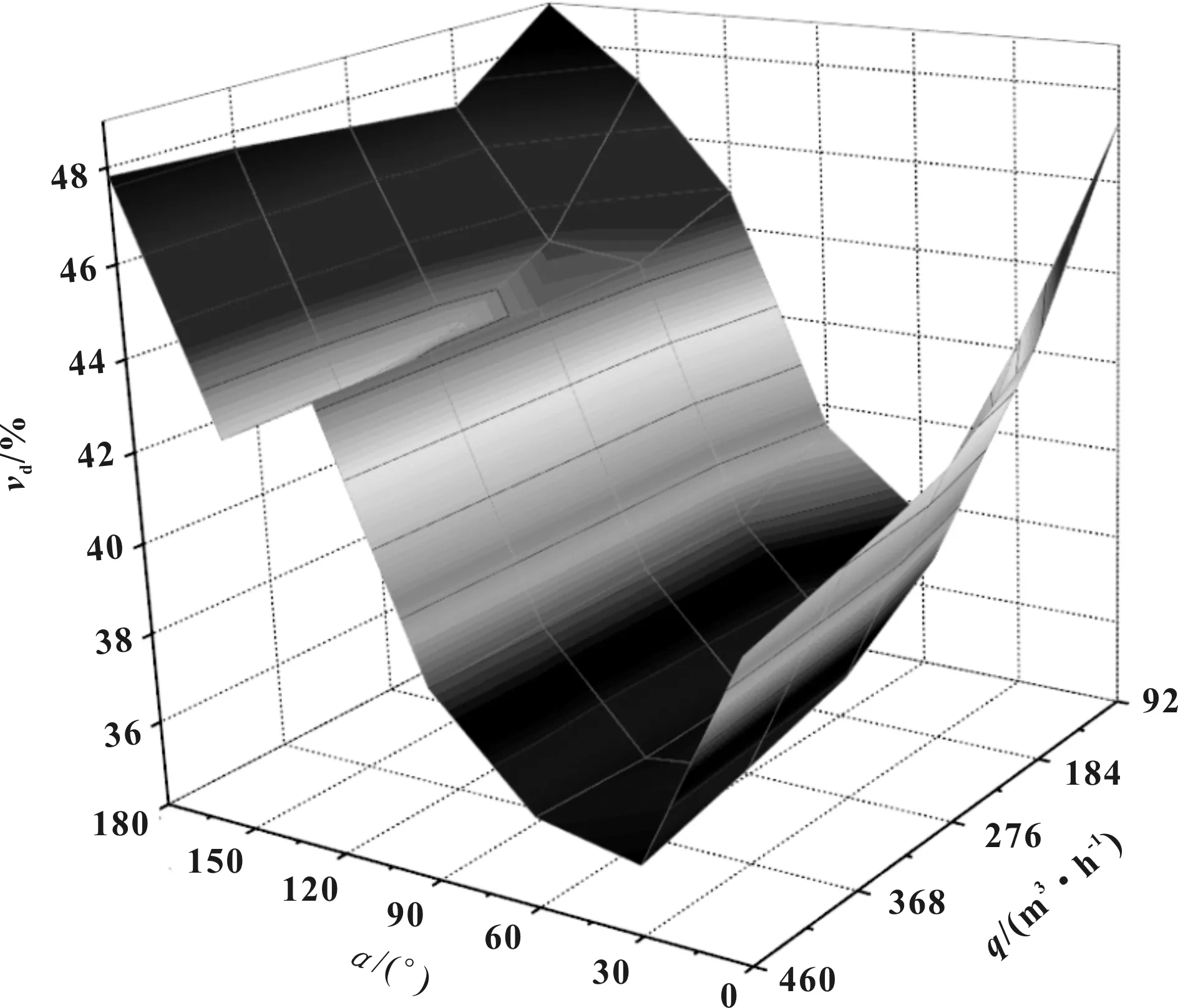
图5 速度偏差云图

图6是不同插入角度的空气流量计在不同的进气系统流量时的入口湍流强度云图，X坐标为插入角度α，Y坐标为进气系统流量q，Z坐标为空气流量计入口湍流强度I。在0°～120°区间，湍流强度I随插入角度α增大而小幅增大，在120°～180°区间，湍流强度I随插入角度α增大而小幅减小。且在低流量区，湍流强度I存在最大值，为5.64%，随流量q逐渐增大，湍流强度I逐渐减小，在高流量区存在最小值，为4.43%。表明湍流强度I受插入角度α影响较小。

图6 湍流强度云图

3.2 插入深度的影响

图7是不同插入深度的空气流量计在不同的进气系统流量时的入口速度偏差云图，X坐标为插入深度h，Y坐标为进气系统流量q，Z坐标为空气流量计入口速度偏差vd。在插入深度h较小且处于低流量区时，速度偏差vd存在最大值，为63.01%。在9～18 mm区间，速度偏差vd随插入深度h增大而大幅减小；在18～27 mm区间，速度偏差vd趋于平缓；在27～36 mm区间，速度偏差vd小幅减小；在36～45 mm区间，速度偏差vd大幅减小且在高流量区出现最小值为31.73%。在45～54 mm区间，速度偏差vd在低流量区趋于平缓，在高流量区小幅增大。表明插入深度h对速度偏差vd影响明显，最大与最小速度偏差之差为31.28%，且在高流量区，速度偏差vd相对更小。存在最佳插入深度区间，使得不同流量下的速度偏差均较小。

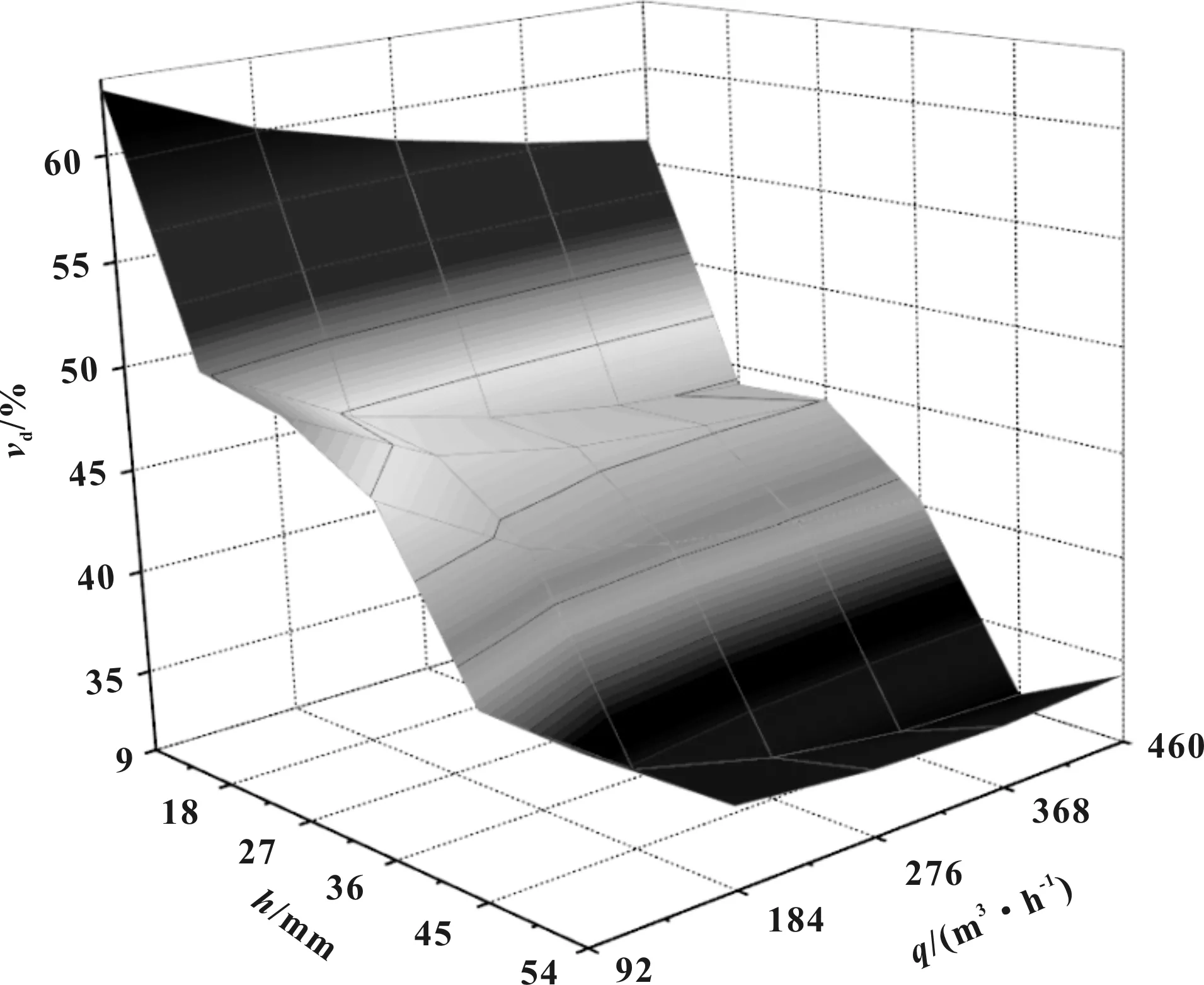
图7 速度偏差云图

图8是不同插入深度的空气流量计在不同的进气系统流量时的入口湍流强度云图，X坐标为插入深度h，Y坐标为进气系统流量q，Z坐标为空气流量计入口湍流强度I。随插入深度h增加，湍流强度I波动小幅减小。在低流量区，湍流强度I存在最大值为5.68%，随流量q逐渐增大，湍流强度I逐渐减小，在高流量区存在最小值为4.37%。表明湍流强度I受插入深度h影响较小。

图8 湍流强度云图

3.3 不同轴向距离的影响

图9是不同轴向距离的空气流量计在不同的进气系统流量时的入口速度偏差云图，X坐标为轴向距离d，Y坐标为进气系统流量q，Z坐标为空气流量计入口速度偏差vd。随轴向距离d增加，速度偏差vd不断增大，最大值为80.52%，且在轴向距离处于较大时，速度偏差vd增大更快。即空气流量计越靠近空气滤清器上壳体出口处，其入口处速度偏差越大。随流量q增加，速度偏差vd小幅减小，最小值为38.01%。表明轴向距离h对速度偏差影响很大，最大与最小速度偏差vd之差为42.51%。

图9 速度偏差云图

图10是不同轴向距离的空气流量计在不同的进气系统流量时的入口湍流强度云图，X坐标为轴向距离d，Y坐标为进气系统流量q，Z坐标为空气流量计入口湍流强度I。在低流量区，湍流强度I随轴向距离增加而波动增大，在中高流量区，湍流强度I随轴向距离增加而不断增大。在低流量区，湍流强度I存在最大值，为5.69%，随流量q逐渐增大，湍流强度I逐渐减小，在高流量区存在最小值，为4.39%。

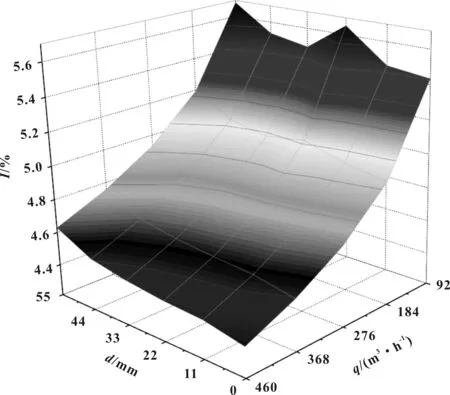
图10 湍流强度云图

3.4 不同圆角半径的影响

图11是不同圆角半径时的空气流量计在不同的进气系统流量时的入口速度偏差云图，X坐标为圆角半径r，Y坐标为进气系统流量q，Z坐标为空气流量计入口速度偏差vd。在中低流量区，当r处于0～3 mm区间时，速度偏差vd存在最大值，为47.29%，且速度偏差vd随圆角半径r增大而大幅减小，当r处于3～6 mm区间时，速度偏差vd趋于平缓，且在5～6 mm区间时有小幅增大。在高流量区，当r处于0～2 mm区间时，速度偏差vd随圆角半径r增大而大幅减小，当r处于2～3 mm区间时，速度偏差vd小幅增大，而后逐渐减小，在4～5 mm区间趋于平缓，且达到最小值，为34.48%，在5～6 mm区间，速度偏差vd增大。表明圆角半径r对速度偏差vd影响较大，且并不是一味增大r就可减小速度偏差vd，存在最佳圆角半径使得速度偏差vd在不同流量下均为最小。

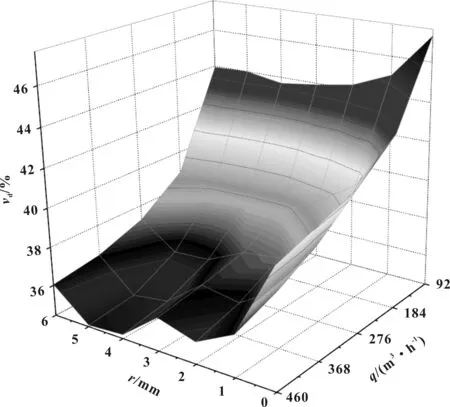
图11 速度偏差云图

图12是不同圆角半径时的空气流量计在不同的进气系统流量时的入口湍流强度云图，X坐标为圆角半径r，Y坐标为进气系统流量q，Z坐标为空气流量计入口湍流强度I。在r处于0～4 mm区间时，随圆角半径r增加，湍流强度I几乎不变，在4～5 mm区间时，湍流强度I增加，且在低流量区增幅相对明显，而后在5～6 mm区间减小。表明圆角半径r对湍流强度I影响较小。

图12 湍流强度云图

4 结论

(1)采用标准k-ε模型对进气系统流场进行数值仿真，并与试验进行对比，验证了该数值方法的可行性。

(2)插入角度α和插入深度h对速度偏差vd影响明显，且在高流量区，速度偏差vd相对更小，存在最佳插入角度和最佳插入深度区间，使得不同流量下的速度偏差均较小。湍流强度I受其影响较小。

(3)轴向距离h对速度偏差影响极大，越靠近空气滤清器上壳体出口处，其入口处速度偏差越大，最大与最小速度偏差vd之差为42.51%。且湍流强度I随轴向距离增加而呈增大趋势。

(4)圆角半径r对速度偏差vd影响较大，且并不是一味增大r就可减小速度偏差vd，存在最佳圆角半径使得速度偏差vd在不同流量下均为最小。湍流强度I受其影响较小。