T 型三电平充电模块的平坦-QPR控制策略

殷 帆，李先允，王书征，卢 乙

(南京工程学院电力工程学院，江苏 南京 211167)

T型三电平由于具有开关器件少，开关管应力较小，总电流谐波较小，功率因数较高，能实现能量双向传递等优势，非常适用于直流充电桩的前级，以实现前级电路的整流以及有源功率因数校正。

T型三电平变换器的动态性能与鲁棒性不仅与电路拓扑结构有关，更与控制策略息息相关。国内外学者对T型三电平的研究主要集中在数学模型、脉宽调制技术、控制策略这三个方面[1]。大量文献对T型三电平的控制策略进行了研究。为解决传统PI双闭环控制动态响应慢、鲁棒性差等缺点，文献[2]提出一种新型双闭环滑模控制策略来提高输出直流侧电压和输入交流侧电流的动态响应速度以及抗干扰性能，其中内环采用无需dq旋转坐标变换的滑模直接功率控制，外环采用电压平方反馈闭环的滑模控制，但该控制器涉及7个参数，参数调节较为繁琐。文献[3-4]提出了功率补偿策略，以克服传统的功率控制策略在电网电压不对称时所产生的谐波，但该功率补偿策略任意时刻只能选择负序电流、有功波动和无功波动中的一种进行控制。文献[5]提出了基于两步预测的有限控制集模型预测直接功率控制策略，可同时实现多个控制目标，并提出了灵活功率控制方法，弥补了传统功率补偿策略的不足，但该控制方法实现较为复杂。

微分平坦理论是一种新颖的非线性控制方法，该控制方法自问世以来，便得到了国内外学者的广泛关注，动态响应速度快是平坦控制最显著的优点[6-7]。QPR控制能有效减小交流电流谐波含量，适用于变流器内环控制，效果显著。本文提出一种复合控制算法，外环基于微分平坦理论进行设计，内环直接在αβ静止坐标系下采用QPR控制。文章详细推导该控制策略的设计过程，并利用仿真验证了该方法的可行性与优越性。

1 T型三电平的工作原理

T型三电平模块的拓扑结构如图1所示。ek(k=a,b,c)为三相交流电源，ik(k=a,b,c)为交流侧输入电流，R为滤波电阻，L为滤波电感，Udc为直流侧输出电压。

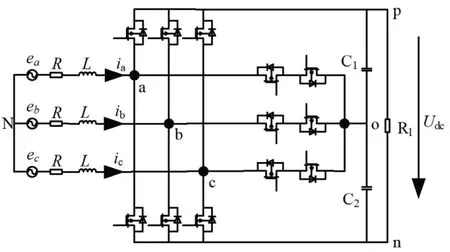
图1 T型三电平拓扑结构

由图1可以看出，该拓扑每一相均有4个开关管，设第k相交流侧电压为uk，当与p点相连的开关管导通时，uko为高电平，与o点相连的开关管导通时，uko为0电平，与n点相连的开关管导通时，uko为低电平。因此，可将T型三电平的开关管等效为单刀三掷开关，如图2所示。

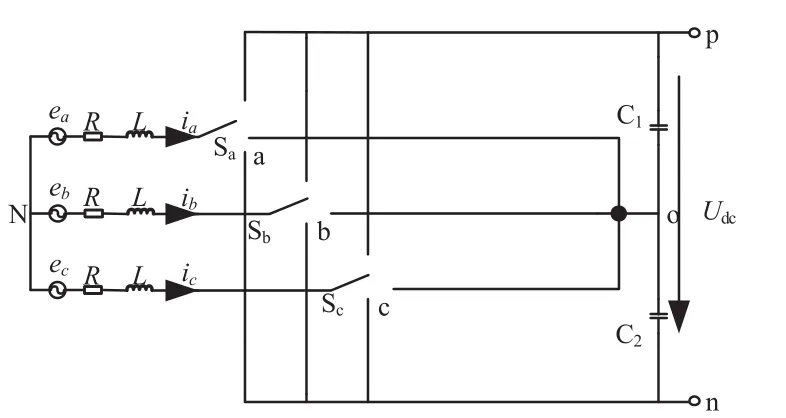
图2 T型三电平等效拓扑结构

三电平变换器的数学模型在文献[8-9]中都有详细推导，限于篇幅，不再赘述。

2 平坦-QPR控制器设计

传统T型三电平控制策略多采用双闭环PI控制，但是PI控制存在动态响应速度慢，需要进行解耦，抗干扰能力较差等缺陷[10]。为解决上述问题，文章提出外环平坦，内环QPR双闭环控制策略，给出详细的设计过程。外环平坦，内环QPR控制框图如图3所示。

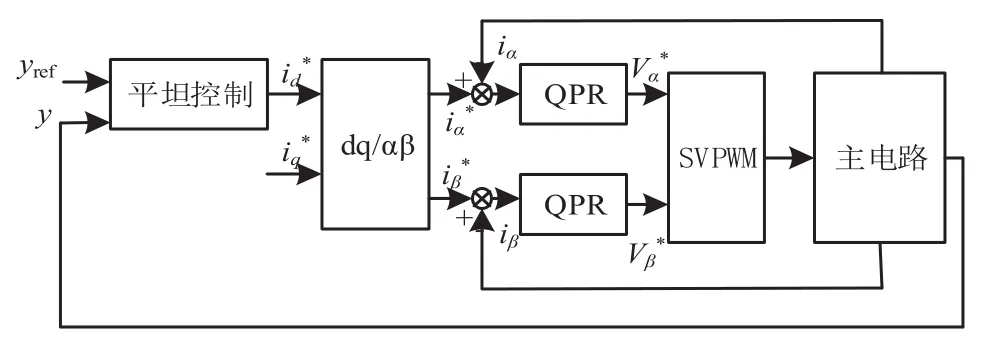
图3 T型三电平变换器双闭环控制框图

2.1 内环QPR控制器的设计

在αβ静止坐标系下采用QPR控制，QPR控制器的传递函数为：

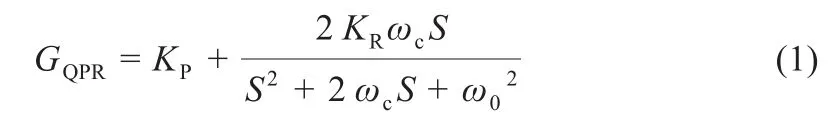
式中：KP为比例系数；KR为谐振系数；ωc为截止频率；ω0为谐振频率。由于电网工频为50 Hz，因此这里ω0为100 π。

设计内环控制器如式(2)所示：

式中：iα*，iβ*为参考值。

QPR控制器的控制性能由KP，KR和ωc决定。KP主要影响系统的带宽和稳定性。随着KP的增大，带宽增大，但谐振效果也被削弱，即频率选择性会降低，不利于系统稳定；KR主要影响谐振频率点处增益；ωc主要影响控制器的带宽。三个参数对控制器性能的影响如图4所示。

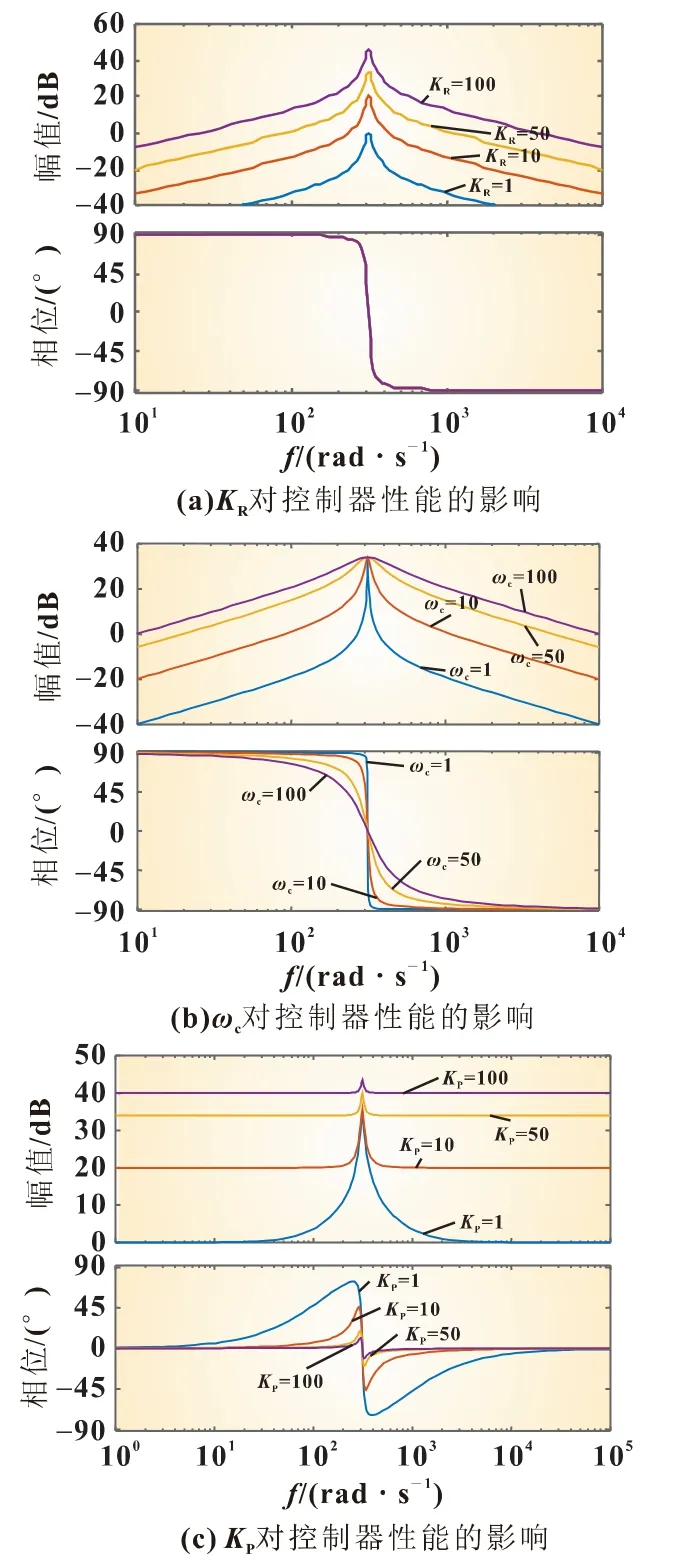
图4 KP，KR和ωc对QPR控制器的影响

根据KP，KR和ωc对QPR控制器的影响并结合物理模型的仿真，最终选择参数KR=1，KP=10，ωc=12。

用MATLAB绘出该参数下的电流内环开环Bode图如图5所示。

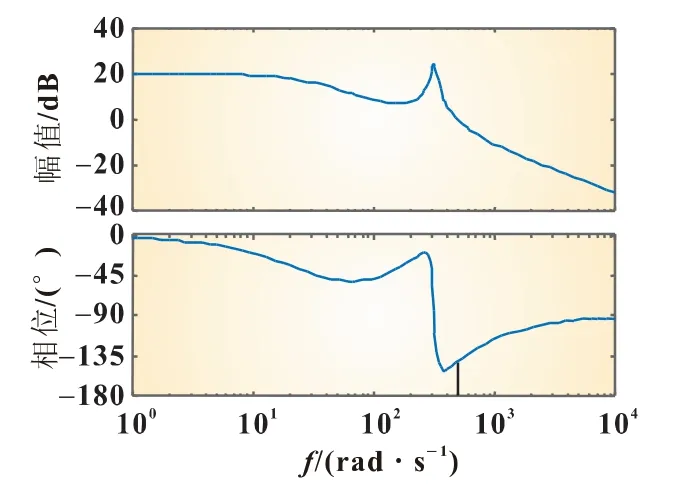
图5 电流内环开环Bode图

系统相频曲线没有穿越-180°，因此幅值裕度为无穷大，而幅频曲线在494 rad/s处穿过0 dB，对应的相角裕度为37.8°，综合幅值裕度和相角裕度，系统稳定。至此，完成内环QPR控制器的设计。

2.2 基于微分平坦理论的外环控制

2.2.1 微分平坦理论介绍

微分平坦理论是一种新型的非线性控制理论，可以显著提升系统的动态特性。假设某一非线性系统的状态变量为x，输入变量为u，输出变量为y，假如该系统可以表示为：

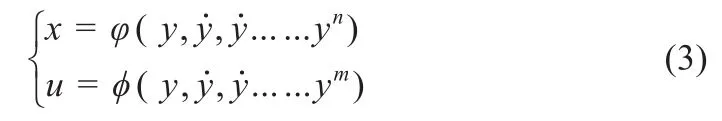
式中：m，n为整数，则该系统满足平坦条件。

微分平坦控制系统包括前馈控制器和反馈控制器两部分，控制系统结构框图如图6所示。图中：yref为参考输出；y为实际输出；u为平坦控制量。

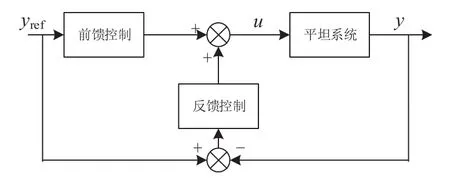
图6 微分平坦控制系统结构框图

2.2.2 外环平坦控制器的设计

基于微分平坦理论的控制方法最重要的是找到满足微分平坦条件的输出量和控制量，并将控制量用输出量及其有限阶导数表示，这样一旦输出量的期望轨迹被确定，控制量就可以确定。

电压外环控制器采用基于微分平坦理论的控制方法，设直流侧电压为Udc，输出电容值c1=c2=c，两电容电压平衡，则每个电容两端电压为直流电压Udc的一半。选取平坦输出y为直流侧两个电容的总能量，电容能量及其微分表达式为：

式中：Rl为直流侧负载；Uc为一个电容两端电压；ic为流过电容的电流；Pdc为直流侧功率。若忽略电路损耗，则交流侧功率P与直流侧功率Pdc相等，选择P为控制量，可得：

式(5)右侧表达式中，包含两个部分：右边第一项为反馈控制量，第二项为前馈控制量。前馈控制量可以直接保留，但反馈控制量只有平坦输出的微分是不够的，由于系统不确定因素的影响，需要引入误差补偿分量。引入两个中间变量e1和e2，表达式如下：

3 仿真及分析

为验证文中所提出的控制策略的可行性与优越性，将该控制策略与传统PI控制进行对比，在PLECS中搭建仿真模型，控制电路仿真参数如表1所示。

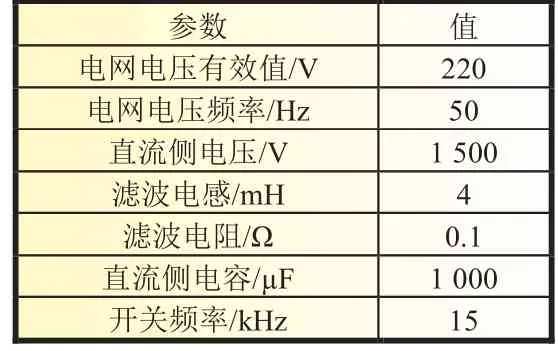
表1 电路参数

控制参数如下：内环QPR控制参数KR=1，KP=10，ωc=12；外环平坦控制参数K1=141.4，K2=5 000。PI控制器内环比例系数KPI=0.4，内环积分系数KII=4，外环比例系数KPV=0.8，外环积分系数KIV=7。同时，为了验证控制器的动态响应速度和鲁棒性，0.2 s负载突变，电阻由原来的45 Ω变为28.8 Ω。图7为T型三电平的直流侧输出电压波形图。

图7(a)波形先上升到最大值然后逐渐稳定到期望值，期间没有经历过多的振荡，0.2 s负载突变时，电压由一个较小的跌落，快速恢复到稳定状态，整体而言波形较为平稳；图7(b)波形经历较多振荡后才逐渐稳定到期望值，负载突变时，又经历了一系列振荡才能恢复稳定，且恢复时间较长。对比图7(a)和(b)可以看出，两种控制方法的调节时间差不多，但PI控制时，电压超调很严重，最高电压接近1 700 V，而且0.2 s负载突变时，外环平坦内环QPR控制可以在短时间内恢复到稳定值，而PI控制不仅电压跌落更大，且恢复时间更长，经过几次振荡后电压逐渐上升，直到0.48 s才能到达稳定值。

图7 T型三电平的直流侧输出电压波形图

图8为交流侧A相电压以及电流波形。可以看出，图中电压电流波形均能保持同相位，这说明在两种控制方法下，T型三电平均能工作在单位功率因数下。0.2 s负载突变时，两种控制方法下电流畸变均较小。

图8 交流侧电压以及电流波形

图9为负载突变情况下系统恢复稳定后交流侧A相输入电流频谱分析。从图9可以看出，频谱中除了基波分量，几乎没有其他谐波，可见两种控制方法下的电流谐波含量都很小，而外环平坦内环QPR控制下的优势更为明显。

为更清晰地看出外环平坦内环QPR的优越性，将两种控制方法的结果对比整理成表2的形式。从表中可以清楚地看出，外环平坦内环QPR控制的稳态特性与动态特性相较于传统PI控制均有一定的优势，调节速度与鲁棒性较强，可见该控制方法可行且具有一定的优越性。

4 结论

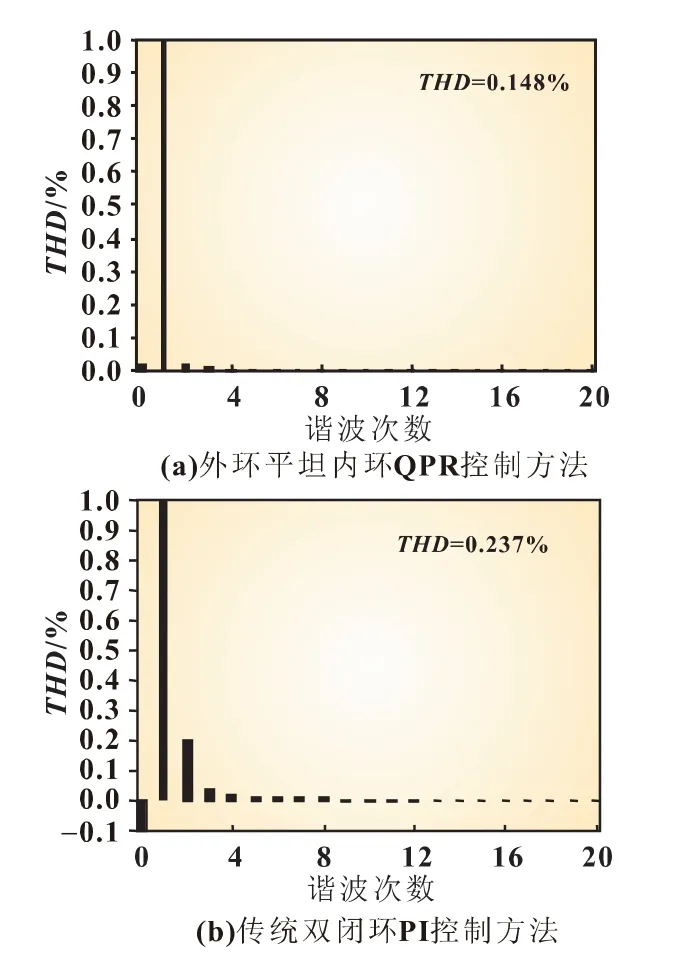
图9 交流侧A相输入电流频谱分析

表2 两种控制方法效果对比

针对T型三电平充电模块传统双PI控制存在动态响应速度慢，需要进行解耦，抗干扰能力较差等缺点，提出一种基于微分平坦理论与准比例谐振控制(QPR)的T型三电平变换器新型双闭环控制策略，给出了详细设计过程。利用仿真将该控制方法与传统双闭环PI控制进行对比，给出了对比波形以及表格，结果表明：外环平坦内环QPR控制系统的动态响应速度以及抗干扰能力都优于传统双PI控制，该控制方法能够满足网侧为单位功率因数，输入电流畸变小，输出稳定等要求，能有效提升直流充电桩的动态响应速度，同时减小网侧谐波。因此，文章所提出的平坦-QPR控制策略具有较为优越的利用价值。