脉宽调制激励下电工钢片动态磁滞特性测量与模拟

刘 圳，张殿海，韩 宇，薛 倩，杨朝晖，任自艳

(1. 中车大连机车车辆有限公司，辽宁 大连 116300；2. 沈阳工业大学辽宁省现代电工装备理论与共性技术重点实验室，辽宁 沈阳 110870;3. 北京新兴东方航空装备股份有限公司，北京 100093)

1 引言

随着电力电子技术的快速发展，变频供电成为现代电驱动系统广泛采用的供电方式。与传统正弦供电方式相比，变频供电由于电压、电流中存在丰富的高次谐波，在电工装备铁心中产生的损耗将显著增加[1,2]。 根据磁特性测量相关标准，现有电工钢片生产厂商仅给出标准正弦磁通密度激励下的磁特性测量数据。这些数据无法准确表征电工钢片在复杂工况下的磁性能[3-5]。为了在设计阶段准确评估并采取有效措施降低铁心损耗进而提高电工装备能效，提出精确测量并模拟脉宽调制(Pulse Width Modulation，PWM)电源激励下电工钢片的动态磁滞特性十分必要[6]。

在电工装备设计阶段，如何计及复杂激励条件对铁心磁特性乃至最终性能的影响是国内外电气行业和学术界研究的热点问题之一。因此，电工钢片复杂磁特性模拟问题是计算电磁学中的重要研究课题之一[7]。它的目标是使用实验中得到的表征电工磁性材料磁特性的相关数据，用数学模型的方式来描述这些参数之间的关系，然后将数学模型与数值分析方法相结合，得到更加准确的性能分析结果[8]。在电工装备设计和计算的过程中应该充分重视电工磁性材料磁滞特性在电工装备性能分析中的地位，建立能够精确模拟磁滞行为的磁滞模型，对其特定材料磁化过程中磁滞行为进行准确数值模拟，这对改善能源利用率，降低能量损耗有着至关重要的作用。

到目前为止，国内外已经发布了正弦磁通密度激励下的电工钢片磁特性测量标准[9]。由于PWM激励下电工钢片磁特性测量与较多因素有关，并且各个影响因素相互耦合，相关测量标准鲜有报道。文献[10]提出了在逆变器供电下制定软磁材料磁特性测量标准方法的可能性，并讨论其影响因素。文献[11-13]使用环样测量方法分别研究激励线圈阻值、载频、负载对测量结果的影响。文献[14]使用爱泼斯坦方圈，研制了PWM激励方式下自动测试系统，推导了铁损测量误差的解析表达式，指出信号的相位差是影响测量精度的关键性因素，经校准后，重复性在3%以内。文献[15]使用单片测量方法，考虑谐波对磁特性的影响，确定参考波形的选取办法，对励磁波形进行控制，得到了PWM激励下铁心数据。文献[16]对PWM激励下高频变压器环形铁心的磁特性进行了测量，并构建了铁心损耗的计算模型。

PWM激励条件下的磁性材料磁特性模拟属于动态磁滞建模问题。频率依赖的动态磁滞模型是指能够模拟宽频范围的磁性材料磁滞行为，在特定频率范围内，其计算值与测量值相近，满足模型的精度要求。文献[17]提出在导电磁性材料中，能够考虑频率因素对磁滞行为的影响的动态磁滞模型。随后，国内外学者进一步探索磁性材料内在机理，将损耗分为：磁滞损耗、涡流损耗和异常损耗三项。随着外场磁化频率的增加，涡流损耗和异常损耗占总损耗的比重随之增大，对总损耗的影响就越发显著[18]。文献[19]发现此理论的不足，对其进行改进，提出基于场分离的动态磁滞模型。但随着电工钢片种类的逐渐丰富，其磁特性越加复杂。此种方法在宽频范围内误差逐渐增大，不能够满足建模精度要求。在2004年，乌克兰学者S. E. Zirka首次提出粘滞模型概念，其改进主要对异常损耗部分进行修改。此后，各国学者在此基础上研究了考虑因素更加全面的频率依赖动态磁滞模型[20-23]。

在原有爱泼斯坦方圈测量标准的基础上，通过对实验平台和测量系统加以改进，研制了电工钢片在PWM激励下的磁特性测量系统。测量了B35A230无取向电工钢片在PWM电源激励下的复杂磁特性。根据磁性材料的回转特性，对一阶回转曲线进行建模，然后与经典JA磁滞模型结合，建立能够精确模拟主磁滞回线中带有局部磁滞回线的模型。结合经典JA磁滞模型和铁耗分离理论，并根据实际测量数据，得到频率对磁滞行为的影响趋势，结合粘滞模型，最终构建出一种适合于电工钢片的频率依赖动态磁滞模型。

2 PWM电源激励下电工钢片磁特性测量

2.1 测量系统的硬件组成

本文所采用的PWM激励下电工钢片磁特性测量系统如图1所示，主要包括：工控机、功率放大器、数据采集卡、低通滤波器、隔离放大器、精密分流电阻和改进的爱泼斯坦方圈装置。通过工控机生成PWM激励信号，经过功率放大器放大之后，送达爱泼斯坦方圈的励磁线圈。为消除高频测量时分流电阻电感效应引起的信号延迟，采用无感精密电阻作为分流器测量励磁线圈中的电流信号。次级线圈与初级线圈并绕，增强耦合，且两者匝数相等。分流器两端的电阻压降和次级线圈两端的感应电压经过隔离放大器的调理，由数据采集卡的模拟输入通道同步采集，严格保证信号序列的对齐，然后将数据传送给工控机进行后序处理。测量用数据采集卡的信号采样频率为1.25 MS/s,测量时爱泼斯坦方圈的初级线圈缠绕在绝缘骨架上。其中，激励线圈的总匝数为700匝。随着激励频率的升高，激励绕组阻抗逐渐增大，为了实现宽频测量，激励线圈采用柔性连接方式，对线圈进行分层绕线，这种方法可以方便地调整激励线圈的匝数。被测样片尺寸为300 mm×30 mm，轧制方向和垂直方向的样片数分别是14。样片之间采用双搭接方式。

图1 改进的爱泼斯坦方圈测量系统Fig.1 Improved Epstein frame measurement system

2.2 激励信号生成及测量原理

本文基于LabVIEW平台编写PWM激励下电工钢片复杂磁特性测量程序。程序主要由PWM激励信号生成、磁通密度B、磁场强度H和铁耗Pc计算等主要模块组成。

2.2.1 激励信号生成

本次测量所需要的PWM电压激励信号通过数据采集卡的模拟输出功能实现，输出波形经过高精度功率放大器放大后激励爱泼斯坦方圈中的电工钢片样品。通过比较调制波(正弦波)和载波(三角波)的方法生成所需的正弦脉宽调制信号，该激励源的特性主要取决于以下参数：

(1) 逆变器直流侧电压Vdc：直流侧电压的大小直接决定了输出PWM脉宽调制信号的幅值。

(2) 调制方法：根据调制技术的不同，可以将PWM分为单极性和双极性。单极性PWM的电压开关在波形的正半周期是从+Vdc到0；在波形的负半周期是从0到-Vdc。双极性PWM的电压开关是从+Vdc到-Vdc。

(3) 载波频率fc：载波频率的大小决定了等效输出波形的精度。同时，从频域的角度看，还与高次谐波出现的位置有关。高次谐波出现的位置为载频与基频之比的正整数倍。

(4) 调制指数m：调制波和载波的幅值之比。

m=E0/Ec

(1)

式中，E0为调制波幅值;Ec为载波幅值;m的大小通常在0～1之间。在脉宽调制技术中，调制指数的大小，不仅决定着输出等效基波的幅值，同时还影响波形中的谐波成分。

PWM信号生成后，不能直接输出，而是需要通过以下顺序励磁。首先，把激励波形复制N个周期。整个波形由黑色粗实线段分为三部分：电压上升段、稳定段和电压下降段，如图2所示。需要说明的是，虽然图2中激励波形为正弦波，但是实际测量时是按照具体激励波形施加的。图中电压上升段可以起到保护的作用，避免对功率放大器以及激励装置的冲击；稳定段中间的虚线框中的阶段用来提取有效波形数据，然后取平均值；电压下降段起到对下一次测量序列退磁的作用，消除样片内剩磁的影响。

图2 激励信号序列示意图Fig.2 Sketch of sequence of excitation signal

2.2.2 测量原理

在改进的爱泼斯坦方圈中激励线圈通以PWM电压激励，待测样片中将会产生交变磁场，此时，爱泼斯坦方圈的感应线圈会产生感应电动势。根据电磁感应定律，磁通密度b(t)波形可通过式(2)计算：

(2)

式中，N2为感应线圈匝数;AB为被测样品截面积；eB为线圈两端感应电动势。

磁场强度波形由励磁电流法测得。通过测量分流器两端的电压可以计算激励线圈中的电流，再由安培环路定律，确定磁场强度h(t)为：

(3)

式中，N1为激励线圈匝数；i(t)为激励线圈中的电流；leff为爱波斯坦方圈中有效磁路长度，根据国标标准，此值为0.94 m。

由坡印廷定理，电工钢片比总损耗可由实验测得的磁场强度h(t)和磁通密度b(t)的波形得到：

(4)

式中，f0为测量频率(基波频率)；ρ为待测样片质量密度。

3 电工钢片动态磁特性模拟

第2节介绍了在脉宽调制激励下电工钢片磁特性的测量方法。基于上述方法测量的磁特性将用于下面动态磁滞模型的建立。

为拓展磁滞模型的应用范围，计及复杂激励条件对电工钢片磁特性的影响，提出能够精确模拟非正弦激励和宽频范围磁滞行为的磁滞模型。

以经典JA磁滞模型为基础，结合能够反映材料回转特性的一阶回转曲线对其进行建模，以获得能够模拟静态或准静态情况下的带有局部磁滞回环的磁滞回线。同时以传统的铁耗分离理论为依据，结合粘滞模型，对异常损耗表达式进行改进，使其能够控制动态磁滞回线的形状，最终达到模拟任意频率下的动态磁滞回线的目的。

3.1 经典JA磁滞模型介绍

JA磁滞模型是在充分研究磁性材料内部能量守恒基础上推导出来的能够描述磁滞回线的微分方程，因此具有明确的物理背景，广泛应用于磁性材料静态磁滞特性的建模。

本文采用经典JA磁滞模型模拟动态磁滞模型的主磁滞回环部分。JA磁滞模型中包括正模型和逆模型两种表达形式。所谓的正模型是以磁场强度H为自变量，磁化强度M为因变量，最终可求得磁通密度B。而逆JA磁滞模型则是以磁通密度B为自变量，磁化强度M为因变量，最终求得磁场强度H。推导逆模型的意义在于与数值计算相耦合。因为，在有限元计算当中，通过矢量磁位A首先可求出磁通密度B，进而得到磁场强度H。因此下面仅介绍逆模型，逆模型可从正模型推导而来，即：

(5)

再根据文献[17]可得逆JA磁滞模型满足的微分方程如下：

(6)

式中，无磁滞磁化强度Man利用郎之万函数来模拟，其数学形式为：

(7)

式中，Ms为材料饱和磁化强度，单位为A/m；a为无磁滞磁化曲线的形状参数，单位为A/m；He为有效磁场强度，单位为A/m；α反映磁畴内部耦合的平均场参数，无量纲；μ0为真空磁导率，其值为4π×10-7H/m；k为磁畴间的牵制系数；δ为方向系数，当dH/dt>0时，其值为+1，当dH/dt<0时，其值为-1；c称为可逆磁化系数。从上面的介绍可知，JA磁滞模型中包含5个参数。这5个参数一般通过对测量得到的磁滞回环进行辨识来确定。目前，国内外学者研究并通常采用现代优化算法实现参数的辨识，由于辨识过程不是本文讨论的重点，因此不做详细介绍。本文采用基于粒子群优化算法的参数辨识方法。

3.2 动态磁滞模型的推导

本节将以静态JA磁滞模型为基础，建立一种能够模拟带有局部磁滞回线和不同激磁频率的动态磁滞模型。

3.2.1 计及局部磁滞回环的磁滞模型

在静态磁化过程中，无论是正弦激励还是非正弦激励，在形成的磁滞回线角度上看，其二者的主磁滞回线形状基本相同，不同点在于，非正弦激励下在主磁滞回线上将出现局部磁滞回环。通过实验观察，在准静态磁特性测量中，其局部磁滞回线的进出点为同一点，即局部磁滞回环自身是处于闭合状态，如图3所示。

图3 正弦与非正弦激励下磁滞回线对比Fig.3 Comparison of hysteresis loops at sinusoidal and unsinusoidal excitation

在准静态磁化上升或者下降的过程中，出现回转点，即出现局部磁滞回线，所体现出的是材料的回转特性。基于此特点，本文使用一阶回转曲线和静态JA磁滞模型结合的方法，建立动态磁滞模型，使其能够精确模拟带有局部磁滞回环的磁滞回线。一阶回转曲线(First Order Reversal Curve, FORC)定义为回转点在主磁滞回线或初始磁化曲线上的各回转线。图4给出了B35A230无取向电工钢在不同磁密回转点Brev的一阶回转曲线。

图4 不同回转点下的一阶回转曲线Fig.4 FORCs at different reversal points

使用郎之万函数对FORC建模，表达式为：

(8)

式中，Brev+、arev+、Brev-、arev-分别为一阶回环曲线模型中的参数。

在建模过程中，已知磁通密度B和模型参数，即可求得磁场强度H。现对FORC模型参数进行辨识。由于FORC函数本身只能构建关于原点对称的函数。但测量得到的一阶回转曲线并非如此。所以，要对已知各FORC进行参数辨识，首先对曲线进行平移处理。例如，如图5所示,对B=0 T下的FORC进行建模，步骤为：

图5 一阶回转曲线建模过程Fig.5 Modeling process of FORC

(1)对回转曲线进行上下平移，使曲线B的最大值和最小值二者绝对值相等。如曲线①。

(2)对回转曲线进行过原点处理。在B为零点时，可知此时的磁场强度H值，所以平移量为此时磁场强度的大小。如曲线②。

(3)根据式(8)，通过函数拟合方法，即可得到最优的模型参数。

(4)通过重复步骤(1)～步骤(3)，即可得到特定材料不同回转点下的FORC模型参数族。

得到FORC模型参数族后，即可精确建模任意回转点下的FORC，建模过程为步骤(1)、步骤(2)取顺序相反操作，最终得到目标回转点的FORC。

在计及局部磁滞回环的准静态磁滞回线中，主磁滞回线用经典JA磁滞模型建模，局部磁滞回线由FORC来建模，其整体建模过程如图6所示，其主要过程总结如下：

(1)首先分析B的波形，确定正向磁化或者反向磁化过程中的回转点(如图6中A点)。

(2)主磁滞回线采用JA磁滞模型建模，即Bmax-A段。

(3)当进入局部磁滞回线时，使用FORC建模。通过FORC模型，可得到局部磁滞回线进入支，如图中AP段。根据对称原理，即可得到完整局部磁滞回线，如图中PC段，C点将与A点重合，即局部磁滞回线进出点重合。

(4)最后，得到带有局部回环的磁滞回线。

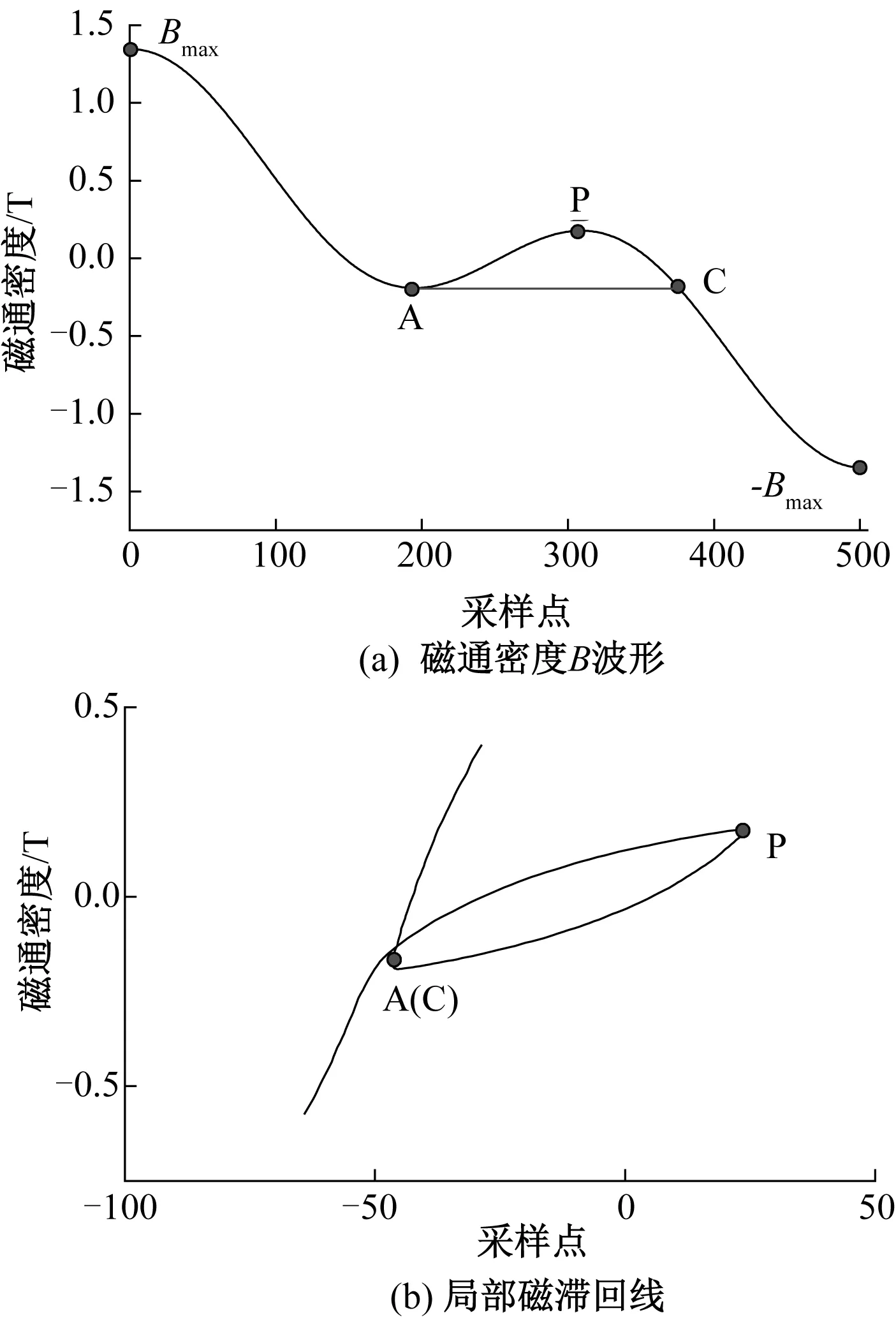
图6 局部磁滞回线的建模过程Fig.6 Modeling process of local hysteresis loop

3.2.2 基于粘滞模型的频率依赖磁滞模型

根据损耗分离理论，将电工钢片铁耗分为磁滞、涡流和异常损耗三项，即：

P=Phys+Pe+Pexc

(9)

式中，Phys、Pe、Pexc分别为磁滞、涡流和异常损耗。在准静态磁化下，一个周期内单位体积的磁滞损耗为磁滞回线的面积，其表达式为：

(10)

式中，T为交变磁场的周期。经典涡流损耗表达式为：

(11)

式中，σ为材料电导率；d为材料厚度；β是几何系数，材料为叠片时其值为6。异常损耗表达式为：

(12)

式中，S为材料的横截面积；G为耦合常数，其值为0.135 6；V0为统计性的耦合场参数，可通过测量得到。由式(11)和式(12)可知，涡流损耗与dB(t)/dt成正比，异常损耗与(dB(t)/dt)1/2成正比。瞬时功率与磁场强度关系为：

(13)

通过式(13)可以得到涡流和异常磁场强度的表达式如下：

(14)

(15)

式中，δ为方向系数，在磁滞回线上升支和下降支中分别代表+1和-1。因此电工钢片中总的磁场强度可表示为：

(16)

最后，用JA磁滞模型算出磁场强度后，加上涡流场和异常场，就可得到总的磁场强度。

对式(16)进行分析可知，实质上相当于在原有磁滞损耗项基础上增加了涡流损耗和异常损耗项。理论上，频率对磁滞行为的影响近似正弦规律，即矫顽力处的影响最大，磁滞回线上下两端点影响最小。但随着电工钢片制造工艺的改进，通过实验测量电工钢片磁特性发现，频率对磁特性的影响并非如此。所以传统的损耗分离计算方法，考虑频率对磁特性的影响，模拟动态磁滞行为，将不再准确。因此，对此进行改进，从异常损耗项入手，通过查阅相关文献和实验验证，提出基于粘滞模型的动态磁滞模型。

粘滞模型可以预测任意频率下的磁滞行为。磁通密度B滞后于磁场强度H可由粘滞模型描述为：

(17)

式中，r(B)通常称为动态磁导率；v是关于材料的常数，它控制模型的动态性；Hstat为静态磁场强度。函数r(B)可表示为：

(18)

式中，Rm是材料常数；最终涡流损耗采用式(14)，而异常损耗则为：

(19)

式中，当v为2时，此时与公式异常损耗项相似。随着研究的深入，通过建模发现式(19)存在一定弊端，早期模型并不能控制动态磁滞回线形状。所以接下来对粘滞模型进行改进，将r(B)改为任意函数形式。目的是选用适当的函数表达式可以满足频率对不同牌号磁性材料所产生的不同磁滞行为的影响。所以，最终r(B)选取为任意多项式函数。基于粘滞模型的频率依赖动态磁滞模型为：

(20)

函数r(B)辨识问题成为了是否能够建立可靠、准确的频率依赖动态磁滞模型的关键。其辨识过程总结如下：

(1)通过实验，可获得两条不同外场频率下的动态磁滞回线，以此作为建模数据。

(2)根据式(20)，推导得：

(21)

式中，Hstat(B)为静态条件下的磁滞回线；H(B)为高频情况下的磁滞回线。即可得到函数r(B)。再通过Levenberg-Marquardt函数拟合方法，最终得到适合表达式。

3.3 动态磁滞模型的验证

本文提出的模拟非正弦激励下动态磁滞模型建模过程分为两个步骤：

(1)模拟带有局部磁滞回环的磁滞回线。

(2)模拟不同频率下的动态磁滞回线。

3.3.1 带有局部磁滞回环的磁滞回线模拟分析

模拟带有局部磁滞回环的磁滞回线主要工作就是辨识静态JA磁滞模型中的5个参数以及不同回转点下FORC参数族。采用粒子群算法对不同磁通密度下的磁滞回线进行参数辨识，辨识结果如表1所示。具体应用时根据待模拟的磁通密度幅值选取合适的参数。

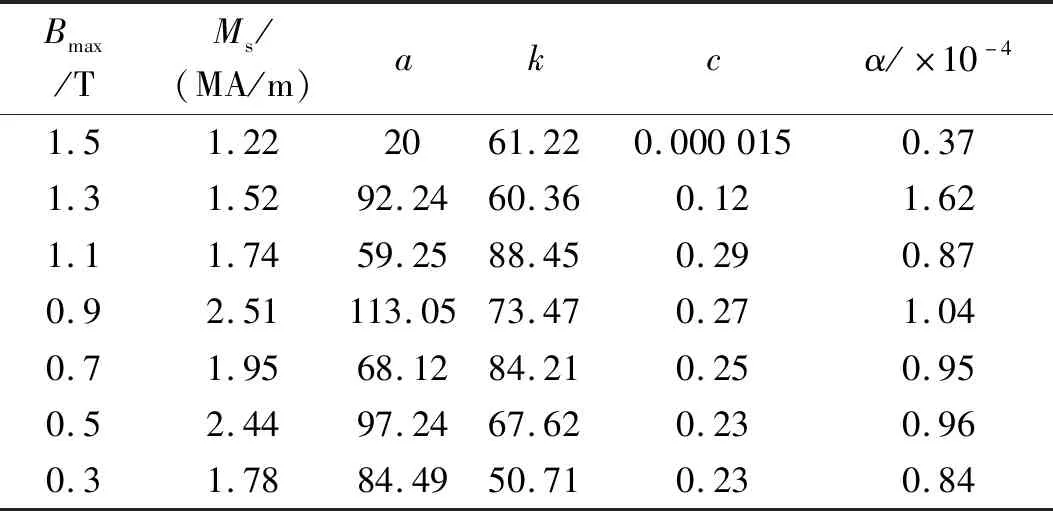
表1 不同磁通密度下JA磁滞模型参数Tab.1 Parameters of JA hysteresis model at different values of magnetic flux density

根据测量得到的一组FORC族，结合式(8)得到不同回转点下的参数族如表2所示。

表2 一阶回转曲线模型参数族Tab.2 Parameters of FORCs at different reversal points

利用辨识得到的参数，验证PWM激励条件下磁滞回线的模拟效果。图7给出了当磁通密度幅值为1.0 T，基波频率为10 Hz，载波频率为200 Hz下的磁滞回线的比较。图7中主磁滞回线中出现了16个局部磁滞回环，局部磁滞回环的个数与载频和基频之比有关。

图7 PWM激励下磁滞回线(B=1.0 T)Fig.7 Hysteresis loop under PWM excitation (B=1.0 T)

3.3.2 不同频率磁滞回线模拟分析

随着激励频率的增加，磁滞回线的面积也逐渐变大，导致损耗上升。采用粘滞表达式r(B)表征磁滞回线形状随频率的改变。根据式(21)，得到频率依赖动态磁滞模型中r(B)合适的函数，四阶多项式函数即可满足建模要求，表达式如下：

(22)

图8给出了激励频率分别为400 Hz和1 kHz下磁滞回线的测量和建模分析结果。可以看出计算值和测量值基本吻合，从而验证了所改进模型的可行性。

图8 不同激励频率下磁滞回线对比(B=1.2 T)Fig.8 Comparison of calculated and measured hysteresis loops under different exciting frequencies (B=1.2 T)

3.3.3 动态磁滞回线模拟分析

3.3.1和3.3.2节分别给出了局部磁滞回线和磁滞回线的频率效应模拟效果，将两者综合即可模拟PWM电源激励下动态磁滞模型。图9为B=1.1 T,基频50 Hz，载频为1 kHz时PWM激励下的动态磁滞回线的对比，两者损耗计算误差仅为1.3%。

图9 动态磁滞回线对比(B=1.1 T)Fig.9 Comparison of dynamic hysteresis loops (B=1.1 T)

4 结论

本文基于传统的爱泼斯坦方圈法，同时考虑到PWM电源激励的测量要求，对测量装置进行了改进。从电工装备实际工况出发，测量了电工钢片在PWM激励下的磁滞特性和铁耗，并提出了计及局部磁滞回线和频率影响的动态磁滞模型。

通过测量结果发现，与传统的正弦激励有所不同，PWM激励由于含有高次谐波，造成主磁滞回环中带有局部磁滞回线，导致损耗增加。

结合经典JA磁滞模型和反映材料回转特性的一阶回转曲线对带有局部磁滞回环的磁滞回线建模效果较好。利用改进的粘滞模型，对材料异常损耗项进行改进，能够模拟不同频率下的动态磁滞回线。最后，将二者综合即可准确模拟PWM激励条件下的动态磁滞特性。