一种基于黏性隐马尔可夫模型的多频带频谱感知方法

贾忠杰，金明，宋晓群

（宁波大学信息科学与工程学院，浙江 宁波 315211）

1 引言

与4G 移动通信技术相比，5G 移动通信技术可将数据速率提高到10 Gbit/s，将时延降低到1 ms，将连接设备数量增加100 倍[1-2]。实现这些需求依赖大量的频谱资源，但是可用的频谱资源，特别是具有良好传播特性的Sub 6 GHz 频谱是有限的，且基本上已经被分配完。大量实测研究结果表明，被分配的频谱资源未得到充分利用[3]。为了给5G 移动通信系统提供充足的频谱资源，提高现有频谱资源的利用率是有效方式之一[4]。认知无线电（cognitive radio，CR）通过机会式接入空闲频段，是目前5G 移动通信系统的研究热点[5-6]。认知无线电利用频谱感知技术检测各频段中的授权用户（primary user，PU）状态。当PU没有占用频段资源时，次级用户（secondary user，SU）可以利用该空闲频段实现数据传输，从而有效提高频谱资源利用率。同时，为了避免对PU造成干扰，SU 必须检测到PU 信号的出现并退出相应频段。因此，频谱感知是实现认知无线电的关键功能。

根据感知频带的个数，频谱感知方法可分为单频带频谱感知和多频带频谱感知。单频带频谱感知方法是对单个频带观测值做出感知决策，常见的方法有能量检测和匹配滤波检测法等[7-8]。单频带频谱感知仅检测一个频带，无法利用其他频段的频谱资源。为了充分提高所有频段的频谱利用率，参考文献[9-14]研究了多频带频谱感知方法。多频带频谱感知方法对多个频带进行频谱感知，当PU 信号再次出现时，SU 能快速切换到其他空闲频带。

多频带频谱感知方法可分为串行频谱感知、并行频谱感知和宽带频谱感知3 类[9]。串行频谱感知在每个时隙检测一个频带，通过轮询方式检测所有频段。参考文献[11]利用PU 在相邻时隙间的马尔可夫状态转移性质，设计了一种自适应转换感知频带机制。但是，这种感知方法耗时随着频带数量的增多而增大。并行频谱感知在一个时隙内对所有频段进行频谱感知。参考文献[12]引入授权用户的活跃性约束，自适应地优化检测周期、感知时间及判决门限，在保护PU 和提高认知网络吞吐量之间进行了权衡。这种方案能有效提升感知速度，但是检测阈值优化较复杂[9]。宽带频谱感知主要利用多频带内授权用户信号的特有性质（如稀疏性）进行检测。参考文献[13]用压缩感知及频谱占用先验信息实现频谱感知，提高了感知性能。参考文献[14]考虑授权用户接入的动态随机性，提出一种动态压缩感知方法来重构时变稀疏信号。然而并不是所有情况都存在频带稀疏性，比如在频谱资源使用频繁的时间段内，压缩感知并不适用。

实际中，某些授权用户极有可能会占据着几个相邻的频带以满足其高速率需求，这样相邻频带很有可能会具有相同的授权用户状态，即相邻频带上的频谱状态具有相关性。为利用多频带中相邻频带相关性，本文通过在相邻频带之间增加黏性因子来增加相邻频带的相关性权重，提出一种基于黏性隐马尔可夫模型[15]的多频带频谱感知方法。仿真结果表明，所提方法具有较快的收敛速度，且接收信号功率估计精度高于其他方法。另外，所提方法在虚警概率为0.1，频带平均占用率为50%，平均信噪比为−12 dB 时能达到接近0.99 的检测概率，并且对比其他方法，检测概率提升了约30%，实现了更高的频谱感知性能。

2 信号模型

假设认知无线电系统对L个频带进行频谱感知。通常，不同频带的授权用户属于不同类型的通信系统（如4G LTE、Wi-Fi 系统等），认知无线电根据自身需求以及授权用户的特点来划分频带，各频带宽度不一定相等。为若干个频带及相应授权用户状态的示意图如图1 所示，其中H0(l)和H1(l)分别表示第l（l=1,2, …,L）个频带内授权用户是静默和活跃的。利用滤波器（如多带滤波器）分别得到各频带的信号，假设第l个频带信号的第n个样本为rl(n)，n=0,1, …,N−1。根据二元假设检验理论：

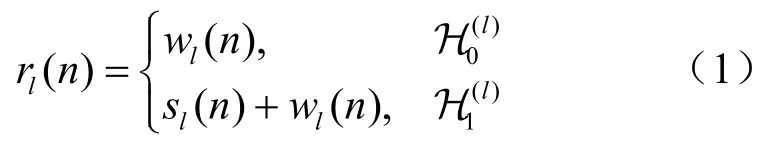
图1 若干个频带及相应授权用户状态的示意图

其中，wl(n) 表示均值为0、方差为的加性复高斯白噪声，即表示第l个频带信号的授权用户信号，假设其均值为0、方差为。

第l个频带上的接收信号测量功率为：

当样本数N充分大时，根据中心极限定理，xl服从高斯分布，即：

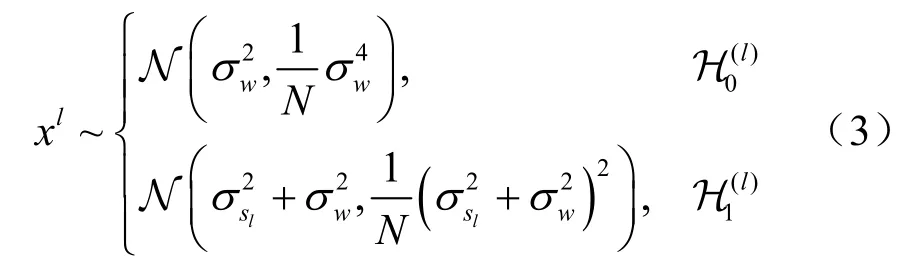
把L个频带上的接收信号测量功率表示成向量形式，为：

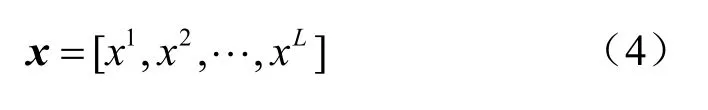
3 基于SHMM 的多频带频谱感知

3.1 频带划分及特性

不同信道的授权用户信号中心频率虽然不同，但是都占据一定的频率范围，所以会有一些相互重叠的情况。以图2 所示Wi-Fi 系统信道为例，每个信道在其中心频率两侧有较宽的延展，很容易看到各信道之间频谱重叠。当某授权用户在其授权频段进行信号传输时，周围频段会因此而停止传输数据，从而降低频谱利用率，因此认知无线电在划分频段时要对带宽进行限制。在实际中，大部分认知无线电在划分频段时的带宽不会太大。这样，由于所划分的每个频段带宽较小，相邻频段一般会有相同的频谱状态。为利用相邻频段的频谱状态相关性，本文利用黏性隐马尔可夫模型来进行建模。

图2 针对Wi-Fi 系统的多带频谱感知频带划分示意图

3.2 黏性隐马尔可夫模型

黏性隐马尔可夫模型包含3 种分布：初始概率分布π、状态转移概率矩阵Q和观测概率分布p(x|z)，其中z=[z1,z2, …,zL]，zl∈{1, 2, …,K}表示第l个频带的隐藏状态，K为隐藏状态总数。隐马尔可夫模型中观测变量xl取决于不可观测状态zl，即zl表示隐藏变量。

针对相邻频带的隐藏变量，状态转移概率为：

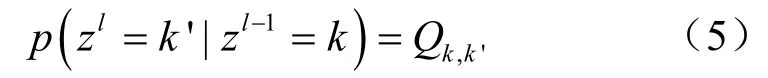
其中，Qk,k'表示从第k个状态转移到第k' 个状态的概率，是状态转移概率矩阵Q中第k行第k' 列的元素，满足：

初始状态转移概率矩阵Q的各行均服从狄利克雷分布，其第k行的分布为：

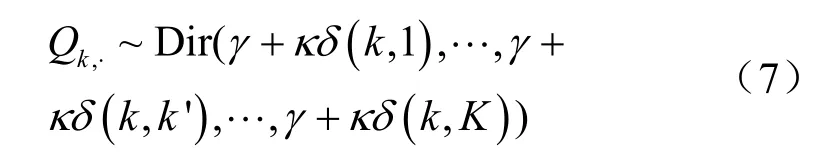
其中，κ表示黏性因子，γ为狄利克雷分布参数，且：

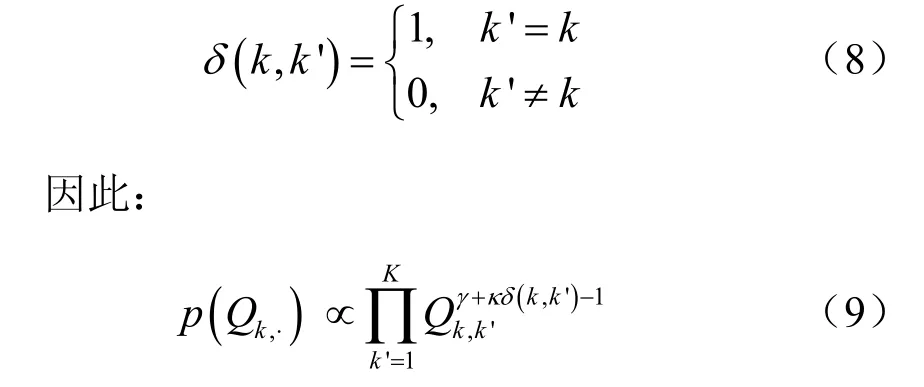
由式（3）可知观测变量xl服从高斯分布。令μk和τk分别为在隐藏变量z l=k条件下xl的均值和精度，则：

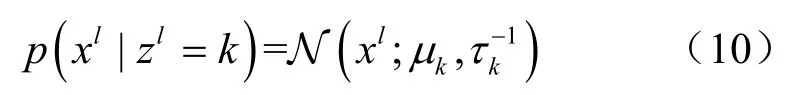
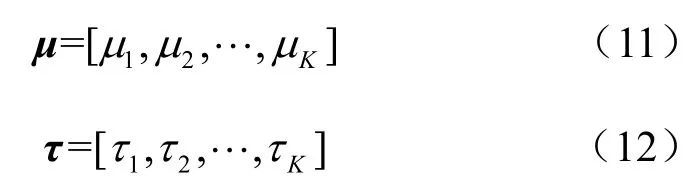
3.3 基于黏性隐马尔可夫模型的频谱感知

基于黏性隐马尔可夫模型的频谱感知过程为如下迭代过程。

步骤1根据贝叶斯定理，可以得到隐藏变量zl的后验分布[16]：

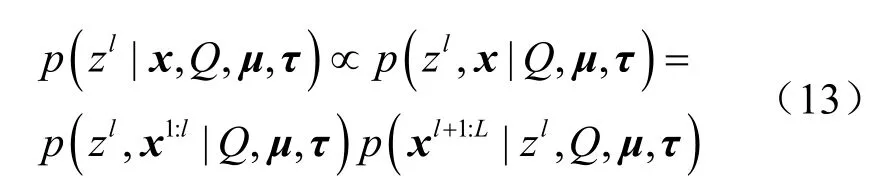
其中， x1:l表示观测向量x中第1 到l个元素所构成的向量，xl+1:L表示x中第l+ 1到L个元素所构成的向量。下面使用“前向后向算法”分析隐藏变量zl的后验分布[17]。定义为前向信息，为后向信息，则式（13）可以写成：

前向信息αl(zl)满足递归关系：

其中，初始化信息α1(z1)为：

同样，后向信息βl(zl)满足递归关系：

其中，最后一个隐藏状态后向信息初始化为βL(zL) = 1。通过前向后向算法得到p(zl|x,Q,μ,τ)后，利用最大后验概率估计隐藏状态zl，即：

步骤2由观测向量x和隐藏向量z计算黏性隐马尔可夫模型的状态转移概率矩阵Q、后验均值μk和后验精度τk，k=1, 2,… ,K。

首先，估计状态转移概率矩阵Q的后验分布。根据贝叶斯定理，状态转移概率矩阵Q的后验分布为：

表示所有频带中从状态k转移到状态k' 的个数。由式（19）可得，Qk,⋅的后验分布为：

所以可以通过式（21）生成后验状态转移概率矩阵Q的各行元素。

然后，估计后验均值kμ和后验精度kτ。在隐藏变量z条件下，观测向量x中元素相互独立，因此：

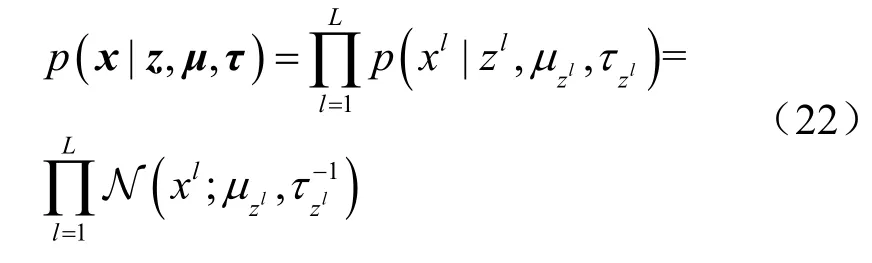
考虑到观测向量x的元素相互独立，因此其均值向量和精度向量的共轭先验服从高斯Gamma 分布，即：

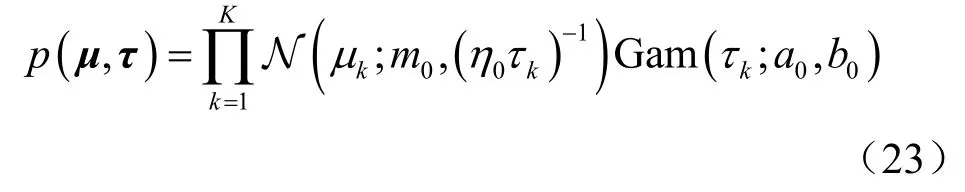
其中，Gam (τk;a0,b0)表示随机变量τk的概率密度函数，τk服从形状参数为a0、速率参数为b0的Gamma 分布。(m0,η0)和(a0,b0)分别表示均值和精度的先验超参数。均值向量μ和精度向量τ的后验分布为：

其中，Lk表示属于第k类的观测变量数量，是所有z l=k的观测变量xl的平均，即：

因此，后验均值kμ和后验精度kτ分别为：

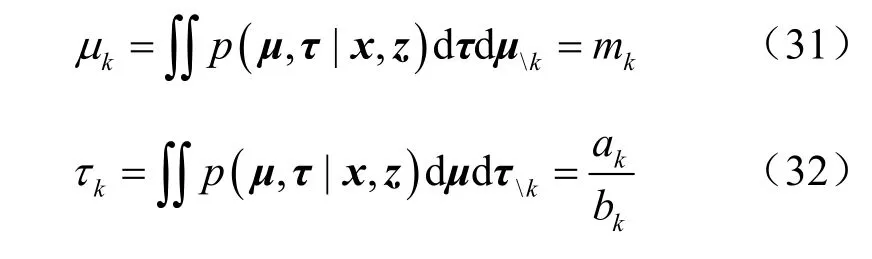
其中，μk表示μ中除去kμ后的向量，τk表示τ中除去kτ后的向量。

通过多次迭代更新参数，可以得到每个类别估计均值μk和每个频带的最终隐藏状态zl。将每个频带对应的估计均值μzl与判决门限λ进行比较，如果μzl大于λ，则判定第l个频带被授权用户占用；否则第l个频带处于空闲状态。算法1给出了具体的算法流程。

算法1基于黏性隐马尔可夫模型的频谱感知

输入观测向量x；初始概率分布π；初始化狄利克雷分布参数γ、黏性因子κ；初始化均值和精度的先验超参数(m0,η0)和(a0,b0)；最大迭代次数T。

输出每个频带的频谱状态。

设置初始均值μk=m0和精度τk=a0/b0，k=1,2, …,K；

fort← 1toT

根据式（7）或式（21）生成状态转移概率矩阵Q；

根据式（16）计算α1(z1)；

根据式（15）和式（17）分别计算αl(zl)和βl(zl)；

根据式（14）计算p(zl|x,Q,μ,τ)；

根据式（18）估计隐藏状态zl；

根据式（31）和式（32）生成均值μk和精度τk，k=1,2, … ,K；

end for

根据zl和μk得到每个频带对应的估计均值μzl，l=1,2, … ,L。

如果μzl<λ，则判定第l个频带被授权用户占用；否则判定第l个频带处于空闲状态。

4 仿真分析

本节通过数值模拟评估所提频谱感知方法的性能。仿真中噪声功率为1mW=。频带中授权用户状态由两个服从不同参数的指数分布随机取整产生：频带状态为0H 的连续频带个数由参数为1θ的指数分布随机取整产生，频带状态为1H 的连续频带个数由参数为2θ的指数分布随机取整产生，如此重复产生若干次。频带的授权用户平均占用率为：

图 3 为不同频带上授权用户功率一个例子。其中指数分布参数为θ1=10 ，θ2=10 ；各个频带的授权用户功率2lsσ在(0.01,10) mW 服从均匀分布。

图3 不同频带上的授权用户功率

黏性隐马尔可夫模型的仿真参数见表1。

分别比较本文提出的基于黏性隐马尔可夫模型、高斯混合模型（Gaussian mixture model，GMM）[18]、K-均值（K-means）聚类[19]、能量检测（energy detection，ED）法[7]和无黏性的隐马尔可夫模型（hidden Markov model，HMM）的频谱感知方法的性能。

表1 黏性隐马尔可夫模型的仿真参数

实验1迭代收敛速度。图4(a)为平均信噪比为−10 dB，频带平均占用率为20%时的平均功率估计误差随迭代次数的变化曲线，其中平均功率估计误差为。平均信噪比表示为信号的平均功率和噪声功率之比。从图4 中可以看出，本文所提方法的平均功率估计误差总是低于其他对比方法。HMM 方法由于未考虑相邻频带相关性，收敛后平均功率估计误差比较高。GMM 方法在100 次迭代后才收敛，而本文所提算法和K-means 方法均在不到3 次迭代时就能达到最终的收敛情况。K-means 方法虽然和本文所提方法收敛速度相近，但本文所提方法的性能优于K-means 方法。

实验2不同迭代次数下的检测概率随平均信噪比的变化曲线如图5 所示。从图5 可见，迭代次数为3 时，GMM 方法和HMM 方法的检测概率性能较差。由图4 可以得知，这些算法并未达到收敛，以致于平均功率估计误差较大，检测性能低。而本文所提方法、能量检测法和K-means方法在迭代3 次时便能实现较好的检测性能。另外，本文所提方法在平均信噪比为−12 dB 时能达到约0.93 的检测概率，且比能量检测法的检测概率高了约0.18。由于达到了迭代收敛，GMM 方法性能均实现了大幅度提升，但仍不如本文所提方法迭代3 次时的性能。而所提方法在多次迭代后，检测性能甚至仍有部分性能的提升。另外，可以看出，在不同的频带平均占用率条件下，所提方法性能一直优于其他对比方法。

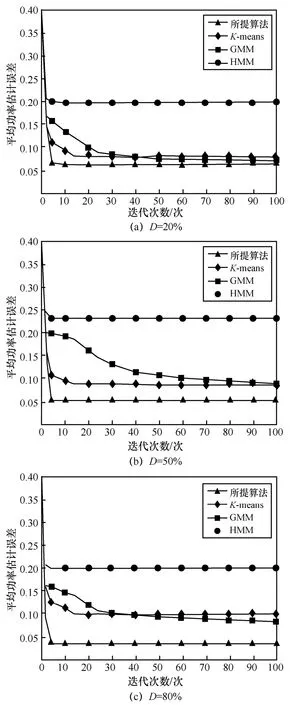
图4 平均功率估计误差随迭代次数的变化曲线

图5 检测概率随平均信噪比（单位：dB）的变化曲线

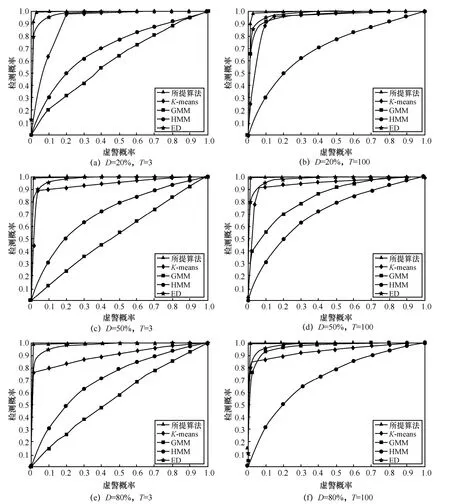
图6 ROC 曲线

实验3不同迭代次数下的接收机操作特性（receiver operating characteristic，ROC）曲线如图6 所示。从图6 中可以看出，所提方法3 次迭代便能实现较好的检测性能，这同样可以由图4得到解释。并且在不同频带平均占用率条件下，所提方法检测概率均高于对比方法。

5 结束语

本文提出了一种基于黏性隐马尔可夫模型的多频带频谱感知方法，该方法通过利用相邻频谱状态相关性来提高多频带频谱感知的检测性能；推导了状态转移概率矩阵、隐藏变量、观测向量后验均值后验精度的迭代计算式。与传统的方法相比，所提方法具有更快的收敛速度、更高的估计精度，从而实现了更高的频谱感知性能。