基于优化模糊控制器的超声波流量传感器智能标定技术
罗 浩
(新疆维吾尔自治区水利科技推广总站,乌鲁木齐 830000)
1 概 述
流量测量是对大量流体运动的量化,流量测量有多种方法,可以是接触式或非接触式传感器,其他间接流量测量方法大多通过测量已知区域内流体的速度来测量流量。从定性和经济角度来看,准确的流量测量是必不可少的。在非接触式流量测量中,超声波流量测量以其分辨率高、噪声对输出干扰小等优点被广泛应用于流量测量,但超声波流量计的非线性特性限制了其应用[1-2]。
为了克服超声波流量计非线性响应特性所面临的限制,本文提出一种智能流量测量技术。通过比较不同算法和方案的最小均方误差(MSE)和回归分析(R),得出最优神经网络。用优化后的神经网络训练系统获得线性度,并使输出适应管径、液体密度和液体温度的变化,所有这些都在一个范围内[3]。
2 超声波流量计
图1所示超声波流量计(UFM)是一种广泛应用于液体流量测量的非接触式流量计。它不仅限于清洁的液体,而且能够精确测量泥浆和不纯净液体的流量。超声波流量计是测量管道中流量的最精确仪表之一。图1显示的是基本超声波流量计的布置,其中管道两侧都安装了发送和接收传感器。接收传感器接收发射传感器从管道一侧倾斜角度发送的超声波信号。接收传感器根据流向计算两个不同的时间,分别称为正向时间和反向时间。这两次(运输时间)的差与管道中的流速成正比。

图1 超声波流量计布置
为了克服超声波流量计非线性响应特性所面临的限制,提出了几种技术,但其中有些是乏味和耗时的。此外,每次管道直径或液体密度发生变化时,需要重复校准过程或更换/调整校准电路。当液体温度发生变化时,超声波流量计的非线性响应特性问题将进一步加剧,因为超声波流量计的输出依赖于温度的变化。从图1可以得出:
(1)
(2)
ΔT=Tup-Tdown
(3)
频率:FIN=1/ΔT
式中:M为超声波信号向前/向后传播的次数;Co为超声波信号在静态流体中的速度;D为管径;V为流体速度。
超声波信号的速度取决于液体的密度,表示为:
(4)
式中:k为体积模量;ρ1为温度t1下的液体比密度;ρ0为温度t0时液体的比密度;Pt1为温度t1下的压力;Pt0为温度t0时的压力;E为液体弹性模量;α为液体温度系数。
UFM的输出是频率,它被应用到信号调节中,然后由频率-电压转换器产生电压。从式(1)-式(4)可以看出,超声波流量计在感应到流量后会产生频率损耗。
3 传统流量测试
图2为传统流量测量技术框图。通过超声波流量计检测以及传输流量信号,最终在超声波流量计输出端将频率转换为有源信号输出,电压转换器设计了校准电路,以映射F-V转换器输出电压对应的流量。

图2 传统流量测量技术框图
传统的校准技术有两个缺点:①这是一个耗时的过程;②只要系统参数(管径、液体密度或液体温度)中的任何一个发生变化,就需要进一步重新校准,从而限制了输入范围的满标度。为了克服这些局限性,智能系统与超声波流量传感器配合,在输入的满量程上产生线性输出,并使系统在管径、液体密度和液体温度变化时更具适应性。
本文将优化后的模糊控制器与超声波流量传感器一起作为智能系统。所设计的优化模糊逻辑模型具有如下属性:①适应管道直径的变化;②适应液体密度的变化;③适应液体温度的变化;④输出与输入流量呈线性关系。
4 方案优化分析
优化后的模糊控制器克服了传统标定电路的缺点,见图3。模糊控制器的输入参数为F-V转换器的输出、被测流体的实际温度、已知管径和液体密度值。以这种方式设计的模糊逻辑控制器产生流量,并用显示器显示。

图3 拟用流量测量技术框图
该模糊控制器模型是利用MATLAB。不同于以调节回路输出电压、管径、液体密度和液体温度的组合作为输入参数,而是以相应的流量作为模糊控制器的输出编辑。通过在级联中添加一个带数据转换器单元的最佳人工神经网络(ANN)模型,克服了前文所讨论的缺点。
开发神经网络的第一步是创建一个用于训练、测试和验证的数据库。特定流量、管径、液体密度和液体温度的数据转换单元的输出电压存储为一行输入数据矩阵。输入流量、管径、液体密度、液体温度及其在数据转换单元输出端的相应电压的各种组合被用来形成输入数据矩阵的其他行。输出矩阵是目标矩阵,由与流量呈线性关系的数据组成,并适应管径、液体密度和液体温度的变化。
找到权重以获得期望输出的过程称为训练。通过考虑隐含层数目变化的不同算法,得到优化的神经网络。均方误差(MSE)是输出和目标之间的平均平方差。MSE值越小越好,当值为0时,表示没有错误。回归(R)衡量产出与目标之间的相关性,回归值等于1表示密切关系,为0表示随机关系。
用4种不同的方案和算法来寻找优化的神经网络。它们是Levenberg-marquardt算法(LMA)、人工蜂群算法(ABC)、蚁群优化(ACO)、由蚁群优化(ACO) BP神经网络。人工神经网络的优化首先假设只有一个隐含层;记录MSE和R值;隐含层增加到2层并重复计算;这个过程持续到4个隐含层。在所有情况下,MSE和R均已注明,见表1。图4和图5为对应于不同算法和隐含层的MSE和R的网格。从表1、图4和图5可以清楚地看出,假设期望的均方误差为阈值,由蚁群算法训练的BP网络能产生最优化的网络。由ACO训练的具有2个隐含层的BP被认为是最优化的ANN,可获得期望的结果精度。
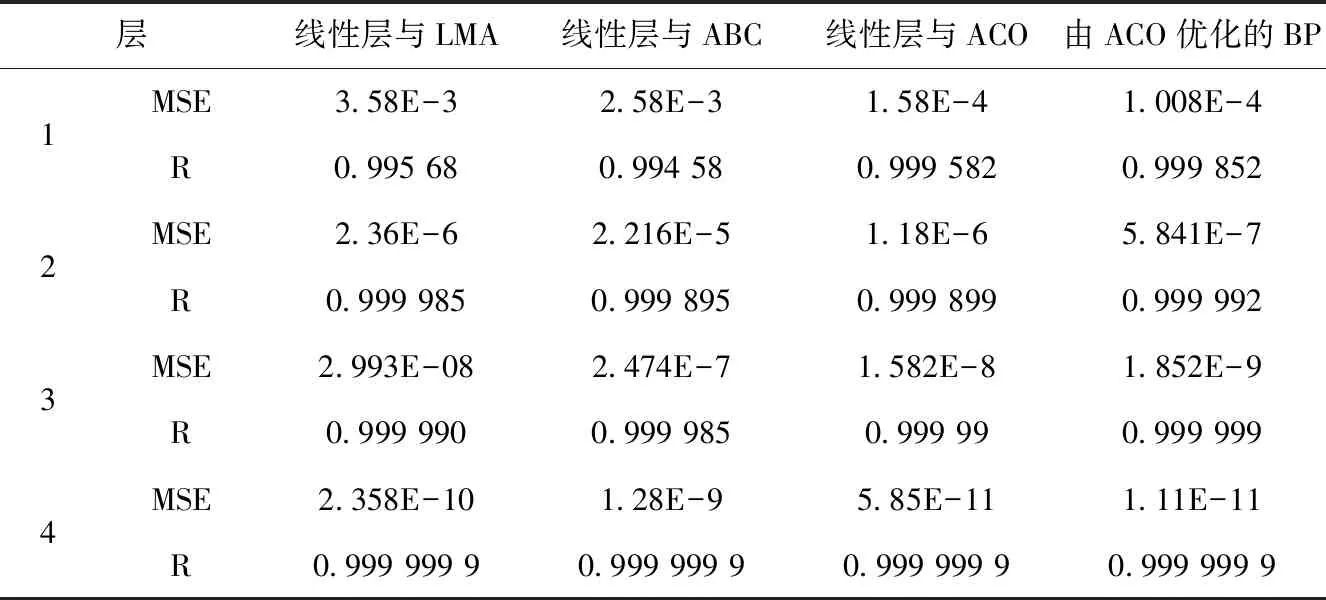
表1 隐含层数与R和MSE的比较

图4 网格显示不同ANN模型对应的MSE

图5 网格显示不同ANN模型对应的R值
根据上述细节对网络进行优化、验证和测试。网络模型优化结果见表2;优化后的神经网络模型的具体参数见表3。

表2 网络模型优化结果

表3 神经网络输入具体参数
5 结 论
用智能模糊逻辑代替传统的标定电路,以适应液体温度、液体密度和管径的变化型号。技术分析表明,采用优化的模糊逻辑模型系统,可以在全尺寸范围内产生线性输入输出特性输入范围。利用仿真数据对优化后的神经网络进行计算、验证和测试。在相应的规定范围内,对不同的管道直径、液体密度和液体温度进行不同的试验输入。最终通过比较基于均方误差最小化(MSE)和回归法的各种方案和算法,考虑一个最优的人工神经网络,其中流量范围为0.0~0.002 5 m3/s,管径范围为0.1~0.3 m,液体密度范围为500~1 500 kg/m3,液体温度为25℃~75℃。

