坡体形状对边坡稳定性影响研究

张 勇，李佳舒，陆振裕

(1.江苏省地质矿产局 第三地质大队，江苏 镇江 212001；2.江苏地质基桩工程公司，江苏 镇江 212001)

1 概 述

边坡结构是一种广泛分布的地质体，在世界各地均有大范围的分布。在地震、强降雨、人工扰动等因素的影响下，边坡结构容易出现失稳破坏，即产生滑坡灾害。滑坡是一种常见的边坡破坏模式，具有破坏性大、多发性强等特征。除此之外，边坡破坏还容易引发堰塞湖、泥石流等次生灾害，这使得其破坏影响的广度和深度再次加大。1960年，意大利某水库发生滑坡事故，造成2 000多人丧生，大面积的房屋被毁；1999年，特大暴雨降临墨西哥，造成大面积的山体滑坡，造成约600人的死亡和失踪，20多万人无家可归；1967年，四川唐山某边坡滑坡，使得雅江堵塞9天，产生了严重的堰塞湖；2008年，汶川地震[1-2]，导致多处山体滑坡，道路被毁，河流被堵，给人民的生命健康和财产造成了严重的影响。

频发的滑坡灾害，巨大的损失，使得科研人员对边坡稳定性的评估更加重视。靳飞飞等[3]基于实际的边坡工程，利用FlAC3D(有限差分软件)对多级高边坡稳定性进行了分析，研究地震荷载作用下的坡体位移、加速度和应力的响应规律，并对边坡的失稳机理进行讨论。何倩等[4]基于某岩质边坡工程，采用PFC2D(离散元)软件对边坡破坏时的运动过程及对应的破坏机理进行分析。结果表明，边坡破坏首先是从边坡中部的破碎岩土层中开始的，在滑体重力的作用下，坡脚处的岩土体开始滑动，而后坡顶逐渐开裂，最终导致边坡的整体失稳破坏，分析结果很好地还原了边坡真实的破坏特征。杨正玉等[5]基于实际工程，采用有限元强度折减法对包含双滑动带的边坡稳定性进行了研究，通过调整抗滑桩的设计位置，提出了双滑动带边坡支护的最优方案。何毅等[6]针对坡顶含有裂隙的土质边坡稳定性进行了分析，结果表明，坡顶倾角角度越大，边坡的稳定性下降幅值越大，同时边坡临界裂隙的深度也会逐渐增大。因此，有必要结合边坡结构本身的特点，对其稳定性进行研究。

近年来，随着计算机技术的发展和边坡稳定性计算理论的进步，很多先进的分析方法被用来分析边坡稳定性。Midas GTS-NX是一款基于有限单元法的边坡稳定性分析软件，可以通过强度折减法对边坡稳定性进行计算，可以获得具体的边坡稳定性计算数值，具有建模方式简单、计算速度快等优势[5]。FLAC3D是一款有限差分的数值分析软件，也可以通过强度折减法对边坡稳定性进行计算，具有收敛性好、模型构建方便等优势[3]。极限分析是一款基于极限理论的分析方法，通过求解边坡安全系数的上限解和下限解来评估边坡的稳定性，可以获得较为准确的边坡滑动带[1]。颗粒流软件也可以用来分析边坡稳定性，将边坡模型简化为离散的颗粒组合而成的结构面，其计算结果较为科学，但其占用的计算资源较为庞大。综上所述，本文采用有限单元强度折减法对边坡稳定性进行研究。

本文以句容市某边坡支护工程为背景，结合坡面的几何特征，采用强度折减法研究坡面几何形状对边坡稳定性的影响，其计算结果可为类似边坡工程提供参考。

2 工程背景

该边坡位于镇江市句容市，其地貌单元为岗地地貌单元。在连续降雨的影响下，边坡坡体出现多处裂缝，部分区域出现局部滑坡现象(图1)。已滑落的坡体长度和宽度分别为60和20 m，滑体体量31 100 m3[5]。

图1 坡体滑坡现场图

参考边坡的几何形状，建立边坡模型见图2。边坡坡体宽度为80 m，高度为20 m。为了消除有限元分析过程中的边界效应，对边坡模型的结合尺寸进行一定的扩展。模型的底部向下扩展40 m，坡脚处坡体水平扩展30 m，坡顶处水平扩展40 m。

图2 边坡模型

3 模型构建

3.1 分析模型

在边坡的实际勘察过程中发现，边坡坡体在几何形状上存在明显的差异。因此，结合边坡的多种几何形状，构建了对应的边坡数值分析模型。可以发现，边坡坡面存在明显的坡上位置和坡下位置，且其分割点为边坡坡面的中点。按照边坡坡面的结合特征，坡面存在外凸、平直和内凹3种典型的形式，因此建立了对应的9种边坡分析模型，分别为：坡下外凸-坡上外凸、坡下外凸-坡上平直、坡下外凸-坡上内凹、坡下平直-坡上外凸、坡下平直-坡上平直、坡下平直-坡上内凹、坡下内凹-坡上外凸、坡下内凹-坡上平直、坡下内凹-坡上内凹。

3.2 模型参数及边界条件

依据地质勘察报告中的边坡土体强度，考虑到数值分析模型的简洁性，边坡采用均质土构建，土体的黏聚力为9 kPa，内摩擦角为12°，重度为19 kN/m3。为了保证有限元的收敛，在分析模型的底部设置固定端约束，即约束水平方向和竖直方向的位移；在分析模型的左右两侧设置水平约束，即约束水平方向的位移。

3.3 网格划分及计算原理

在数值分析模型中，网格划分质量的好坏对边坡稳定性的分析结果具有重要的影响，因此需要对网格尺寸进行设置。本文基于剪切耗散能，采用自适应网格划分的方式对边坡网格进行划分。在网格划分过程中，首先对边坡中的网格进行一次划分，然后依据剪切耗散能的大小对部分网格区域进行二次划分，即自适应。这样既可以保证网格划分的质量，同时又控制了网格划分的数量，达到提高边坡稳定性分析效果的目的。在本文中，初始的网格设置为6 000单元，自适应网格划分次数为3次， 每次1 000网格。网格划分的效果见图3。

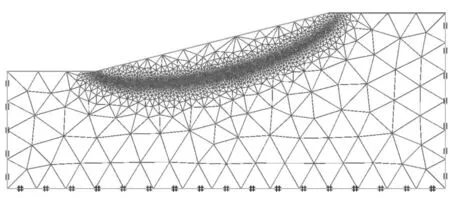
图3 网格划分效果图

在数值分析模型中，网格划分质量主要是对分析精度产生影响，而分析方法直接影响边坡稳定性的分析结果。强度折减法是一种典型的边坡稳定性分析方法，不仅可以直观地量化边坡的安全系数，同时可以反映边坡的剪切带发展模型，对于边坡稳定性分析具有重要意义。在分析过程中，通过对边坡中土体强度(黏聚力、内摩擦角)的不断折减，结合模型的收敛特性，来判断边坡的安全系数。

边坡收敛性判断主要包括3个方面：①边坡数值分析模型是否收敛；②边坡剪切带是否贯通；③边坡是否达到人为设置的其他收敛条件。当判断边坡收敛后，土体强度的折减系数就是边坡的安全系数。

4 结果与讨论

边坡稳定性分析结果见图4。

由图4可知，不同边坡坡面几何形状下，边坡的安全系数和对应的破坏模式均不相同。对于“坡下外凸-坡上外凸”(图4a)的破坏模式，边坡的安全系数为0.940，可以发现边坡的剪切带沿着坡下进行发展，使得边坡发生局部滑坡；对于“坡下外凸-坡上平直凸”(图4b)的破坏模式，边坡的安全系数为0.940，可以发现边坡的剪切带沿着坡下进行发展，使得边坡发生局部滑坡，这与“坡下外凸-坡上外凸”的边坡破坏模式相同；对于“坡下外凸-坡上内凹”(图4c)的破坏模式，边坡的安全系数为0.939，可以发现边坡的剪切带沿着坡上进行发展，使得边坡发生局部滑坡；对于“坡下平直-坡上外凸”(图4d)的破坏模式，边坡的安全系数为0.925，可以发现边坡的剪切带沿着坡上进行发展，使得边坡发生局部滑坡；对于“坡下平直-坡上平直”(图4e)的破坏模式，边坡的安全系数为1.232，可以发现边坡的剪切带沿着边坡整体发展，边坡形成整体滑坡；对于“坡下平直-坡上内凹”(图4f)的破坏模式，边坡的安全系数为0.940，可以发现边坡的剪切带沿着坡上进行发展，使得边坡发生局部滑坡；对于“坡下内凹-坡上外凸”(图4g)的破坏模式，边坡的安全系数为0.728，可以发现边坡的剪切带沿着边坡整体发展，边坡形成整体滑坡；对于“坡下内凹-坡上平直”(图4h)的破坏模式，边坡的安全系数为0.911，可以发现边坡的剪切带沿着坡下进行发展，使得边坡发生局部滑坡；对于“坡下内凹-坡上内凹”(图4i)的破坏模式，边坡的安全系数为0.940，可以发现边坡的剪切带沿着坡上进行发展，使得边坡发生局部滑坡。

通过边坡剪切带发展位置与边坡稳定性之间的关系可以发现，整体滑坡时，边坡的安全系数最高；“坡下内凹-坡上外凸”时，边坡的安全系数最低。

图4 边坡稳定性分析结果

5 结 论

结合镇江市句容市某边坡支护工程，研究了坡面几何形状对边坡稳定性的影响，具体结论如下：

1) 采用强度折减法分析边坡稳定性，不仅可以获得边坡的安全系数，同时可以获得边坡的剪切破坏面位置。

2) 对比不同的坡面形状发现，“坡下内凹-坡上外凸”时，边坡的安全系数最低；“坡下平直-坡上平直”时，边坡的安全系数最高。

3) 通过边坡剪切带发展位置与边坡稳定性之间的关系可以发现，整体滑坡时，边坡的安全系数一般是高于局部滑坡时的边坡安全系数。