被动网冲击变形解析解及足尺试验对比研究

敖跃齐 罗 磊

(1.重庆大极建筑工程有限公司，重庆 400000； 2.四川奥思特边坡防护工程有限公司，四川 成都 610000)

1 概述

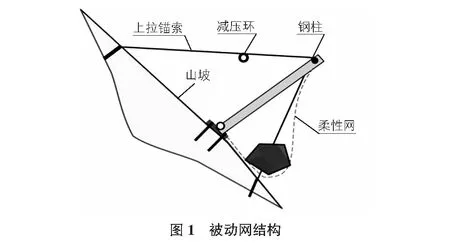
被动网主要由支撑结构、柔性网片以及减压环构成，其支撑结构由钢柱、基座、锚杆构成；柔性网片由上下支撑绳、上下拉锚绳、环形网以及双绞六边形网构成，如图1所示。

近年来，针对被动柔性防护网系统缓冲性能的研究多采用足尺冲击试验与数值模拟[2-13]。其中，Escallón等[5]根据欧洲规范ETAG027建立了一种被动柔性防护网系统，并进行了1 000 kJ足尺冲击实验和数值模拟，支撑绳在柱端通过滑轮实现滑动，由于支撑绳上悬挂的网环极易在滑轮处形成卡阻进而造成锁死，因此系统缓冲能力十分有限，足尺试验显示，其最大冲击变形仅为4.36 m。Kwan等[4]基于我国香港佐敦谷的实地考察，并结合反演分析，发现标称能级为1 000 kJ的防护系统虽然成功拦截能量约为463 kJ的落石冲击，但钢柱严重损坏，系统丧失防护能力，究其原因，与消能装置没有启动，导致系统冲击变形能力不够有直接关系，实测与计算均表明其冲击变形仅约2.5 m。Escallón[5]改进了支撑绳滑移变形控制方法，通过释放柱端附近支撑绳上的数个网环，形成了卡阻“规避区”，延缓了变形锁死，最大冲击变形增加至约9 m，提高了系统缓冲性能。但因“规避区”的存在，导致网片有效支撑长度减少，降低了系统的拦截高度，同时，由于“规避区”尺寸限制，支撑绳滑移变形量有限，因此无法适应高冲击能量条件下的大冲击变形需求。Gottardi等[11]开展了系列被动柔性防护网系统的足尺冲击试验。对于2 000 kJ～5 000 kJ的系统，则通过引入过渡绳的方式，其滑移控制原理与Escallón[5]相似，差别仅在于过渡绳可为“规避区”网环提供支撑，并承受局部悬挂网片上的少部分荷载。更重要的是，通过跨越柱端设置过渡绳来提高缓冲性能的方式实际上并未减轻支撑绳的负担，制约了系统缓冲性能的进一步提高。

2 大变形解析

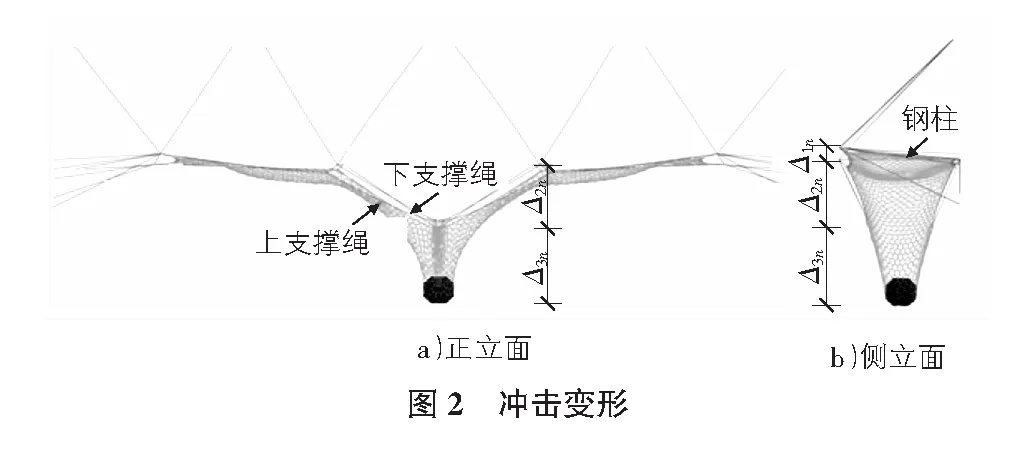
既有研究表明，落石冲击过程持时极短，经统计约为0.2 s～0.5 s，持时与冲击变形量s直接相关。被动柔性防护网系统冲击变形如图2所示，由支撑结构变形Δ1n、支撑绳牵引消能器伸长引起的滑移变形Δ2n、网片冲顶变形Δ3n等构成，其量值可达10余米，准确估算系统冲击变形量，可为系统选型与设计提供重要依据。

2.1 支撑结构变形

被动柔性防护网系统的支撑结构由支撑钢柱及与之相连的拉锚绳组成，其变形通常包含材料弹塑性变形及钢柱转动变形，比较而言，材料弹塑性变形可忽略不计，因此，该部分变形主要取决于拉锚绳消能器伸长所引起的钢柱转动。由于冲击跨与相邻跨拉锚绳内力不同，相应的消能器伸长量不同，可引入工作系数对其拉伸量分别进行修正。假定冲击跨拉锚绳伸长后长度为L1，相邻跨拉锚绳伸长后长度为L2，可根据变形前后的支撑结构位形建立空间几何关系，采用几何解析确定支撑结构变形产生的冲击变形量Δ1n：

Δ1n=H-h=LAB′·cosα-(Hd-Hpsinβ)

(1)

(2)

(3)

(4)

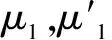
2.2 支撑绳滑移变形

冲击作用发生后，由于支撑主绳消能器的拉伸变形，冲击区域支撑主绳会发生“V”形变形，并且与卸扣直接相连的部分会形成弧形区域，该区域的长度可假定等于落石的尺寸ws，并且由于该区域弧度较小，因此，其宽度w可近似等于其长度ws。根据足尺试验和欧洲规范，被动柔性防护网系统的残余拦截高度hR大致为0.5Hp，因此，可假定该“V”形变形区域在水平方向上两侧的收缩变形为0.25Hp。初始支撑主绳与水平面的夹角φ较小，可近似视为φ≈0°，即跨中支撑主绳的初始长度近似等于钢柱间距Ld。因此，沿冲击方向的变形量Δ2n可通过几何分析确定：

Δ2n=

(5)

其中，Ld为钢柱间距；ws为落石尺寸；μ2l,μ2r分别为左右支撑绳主消能器的效率系数；Δ2l,Δ2r分别为左右支撑主绳消能器的实际极限拉伸长度。

引入修正系数φt进行折减。l可按式(6)计算确定：

(6)

其中，φt取0.8。因此，支撑绳消能器的实际极限拉伸长度Δ2需按式(7)确定：

(7)

其中，Δ2为消能器设计极限拉伸量。

2.3 网片冲顶变形

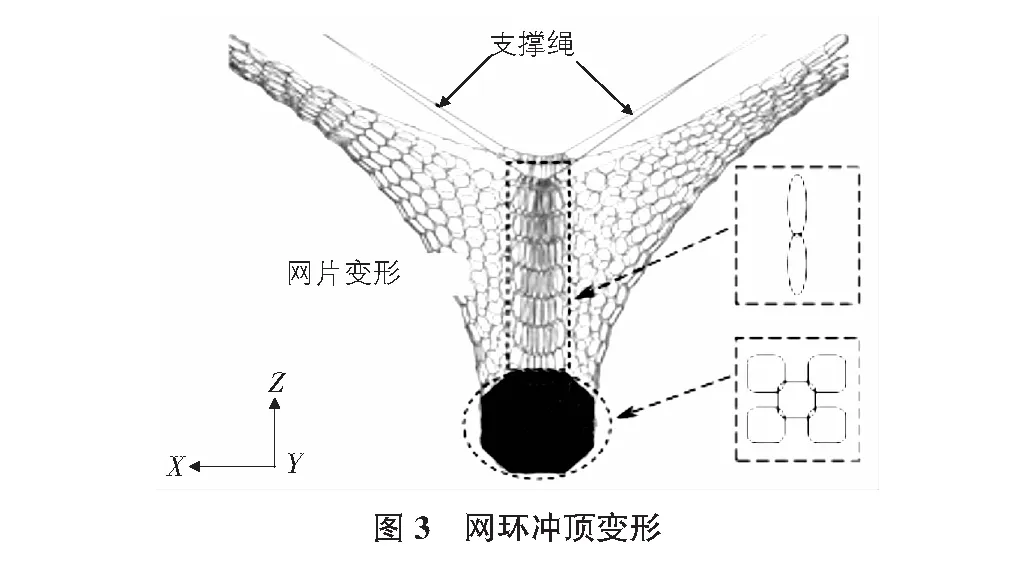
如图3所示，网片遭受落石冲击作用后，网环会发生对径拉伸及对角拉伸等变形。柔性网的横向长度远小于纵向，且纵向的松弛特征非常显著，网片的冲击传力变形特征与单向板类似，即横向网环的受力远大于纵向网环，因此，其冲顶变形主要取决于横向网环的变形，这在试验与数值模拟中得到验证：横向网环发生明显的对径拉伸弹塑性变形，而纵向网环几乎处于弹性拉伸阶段。因此，对于冲顶变形Δ3n，可以按照几何关系近似求解：

(8)

(9)

其中，Ln0为横向网环初始长度，可近似等于支撑钢柱高度Hp；D为网环的直径；ntotal为拦截高度上连续相连网环的个数；ndiagonal为顶头包裹面上的网环数量；Ln为网片对径拉伸之后的理论长度；φi为网片对径拉伸发育系数，网片周边为固定边界时，可取经验值0.6，为绳索支撑时，可取经验值0.7。

3 落石冲击足尺试验

试验模型共三跨，每跨10 m，拦截网片呈水平状态，共设置4根标高为5 m的钢柱。采用龙门吊将重为7 500 kg的试块提升距网片20 m高，冲击位置为中跨网片的中心，冲击能量为1 500 kJ，为了防止系统出现卡阻现象，将所有减压环均置于支撑绳的最外侧；共进行三次冲击试验。

3.1 冲击过程

落石释放后0.1 s，落石与拦截网片充分接触，仅中跨网片变形，边跨维持不动；0.2 s，在试块作用下，边跨网片向中跨运动，带动支撑绳向中跨滑移，中跨网片变形明显；0.3 s，中跨钢柱同时向外、向下偏摆，网片产生巨大形变；0.38 s落石达到最大竖向冲击位移，而后向外滚动；0.5 s落石基本稳定，见图4。

3.2 变形特征

冲击试验均成功拦截落石，提取各模型中冲击点位移(即网片变形)、支撑绳位移以及端柱的竖向位移极值(见图5)。

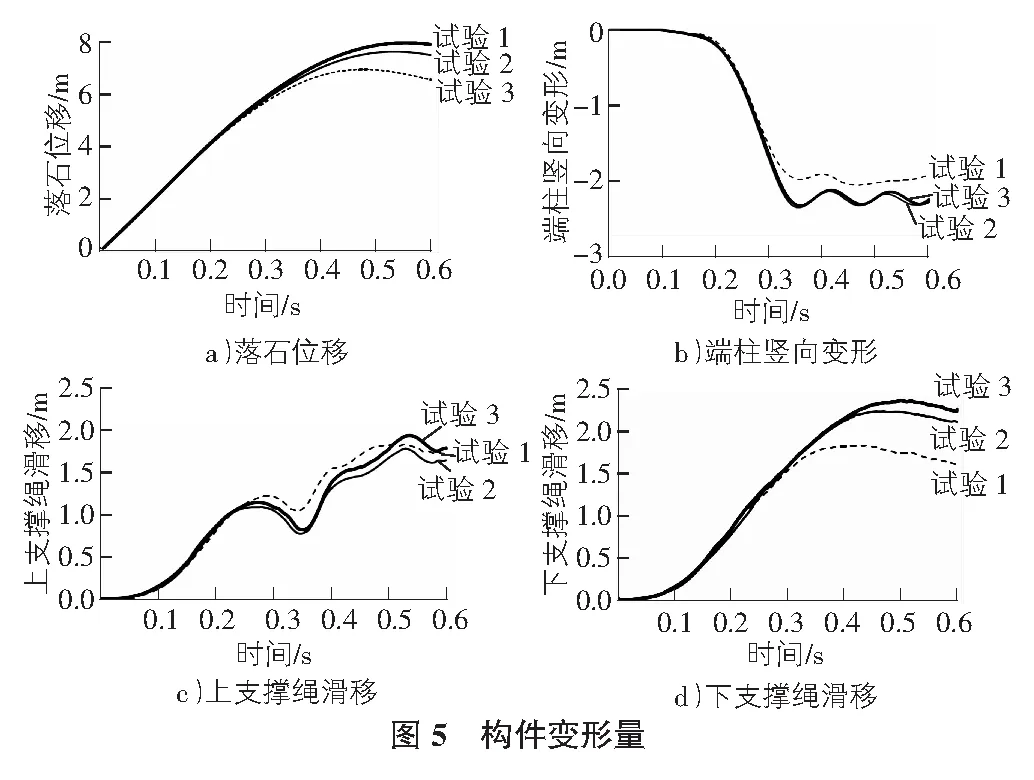
由解析计算公式得到的系统各变形分量与总体冲击能力与数值计算结果吻合较好(见表1)，系统总体冲击能力最小误差仅为0.8%，最大误差为8.6%，说明解析计算公式计算结构的冲击能力具有较高的准确性。

表1 变形分量计算对比

4 结语

1)被动柔性防护网结构的拦截全过程是通过整体变形协调的过程，依靠系统的大变形消散冲击能量，各构件的变形有着内在的相关性。2)提出被动柔性防护网各构件在冲击荷载作用下变形的解析计算方法，并通过落石足尺冲击试验对比验证了其正确性。3)由于足尺试验局限性，后续通过更多组、不同能级足尺的落石冲击试验进一步的验证被动网防护系统的受力、变形，以及验证解析解的结果。